
Vektory: násobenie konštantou, súčet, rozdiel

Súčet vektorov
Vektory \vec{u} a \vec{v} sčítame takto: počiatočný bod vektora \vec{v} posunieme do koncového bodu vektora \vec{u}. Súčet vektorov \vec{u} a \vec{v} je vektor \vec{w}, ktorý má počiatočný bod rovnaký ako vektor \vec{u} a koncový bod rovnaký ako vektor \vec{v}. Píšeme: \vec{u}+\vec{v}=\vec{w}
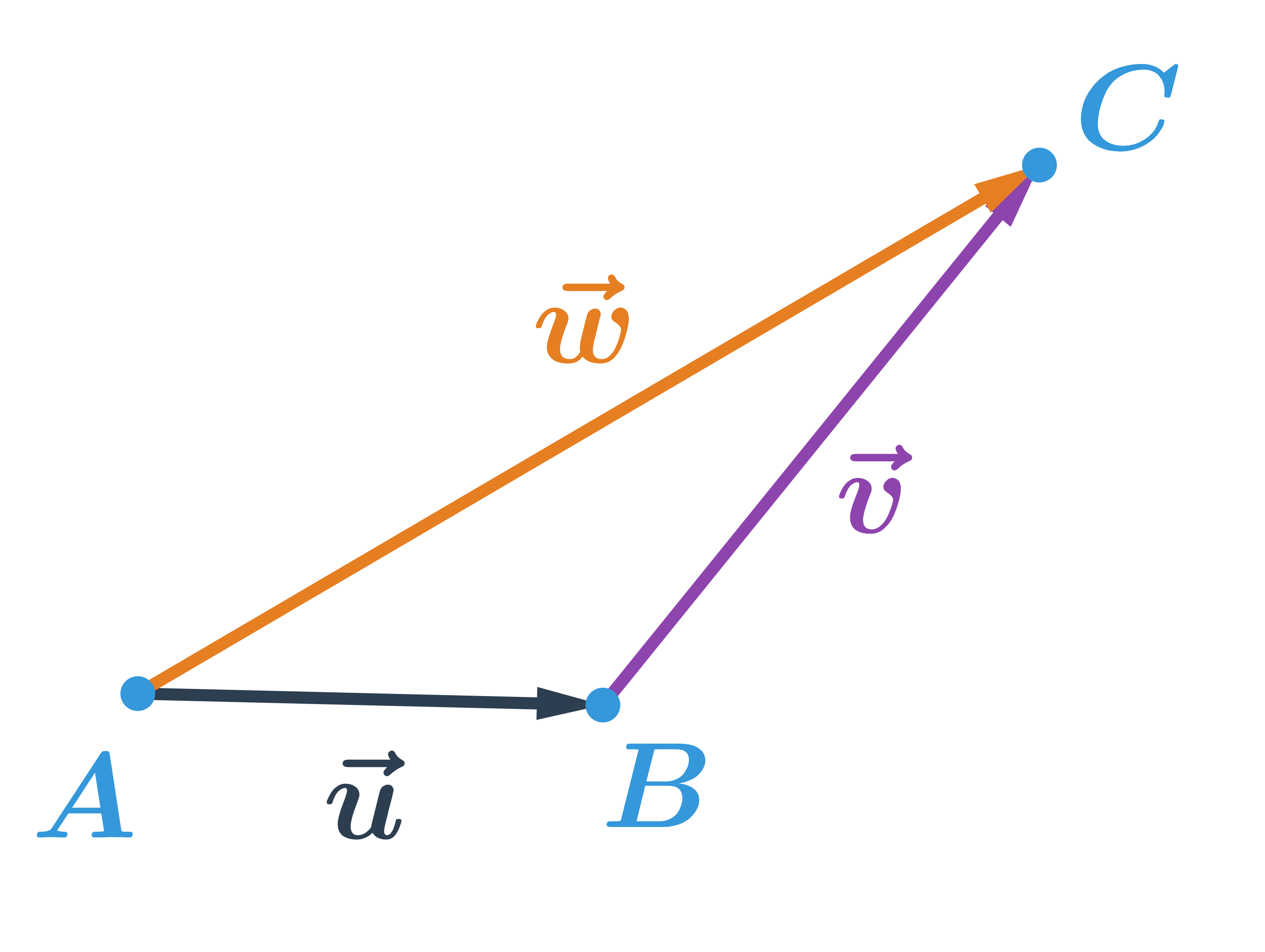
Vektory na obrázku sú označené \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{BC}. Súčet týchto vektorov: \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}
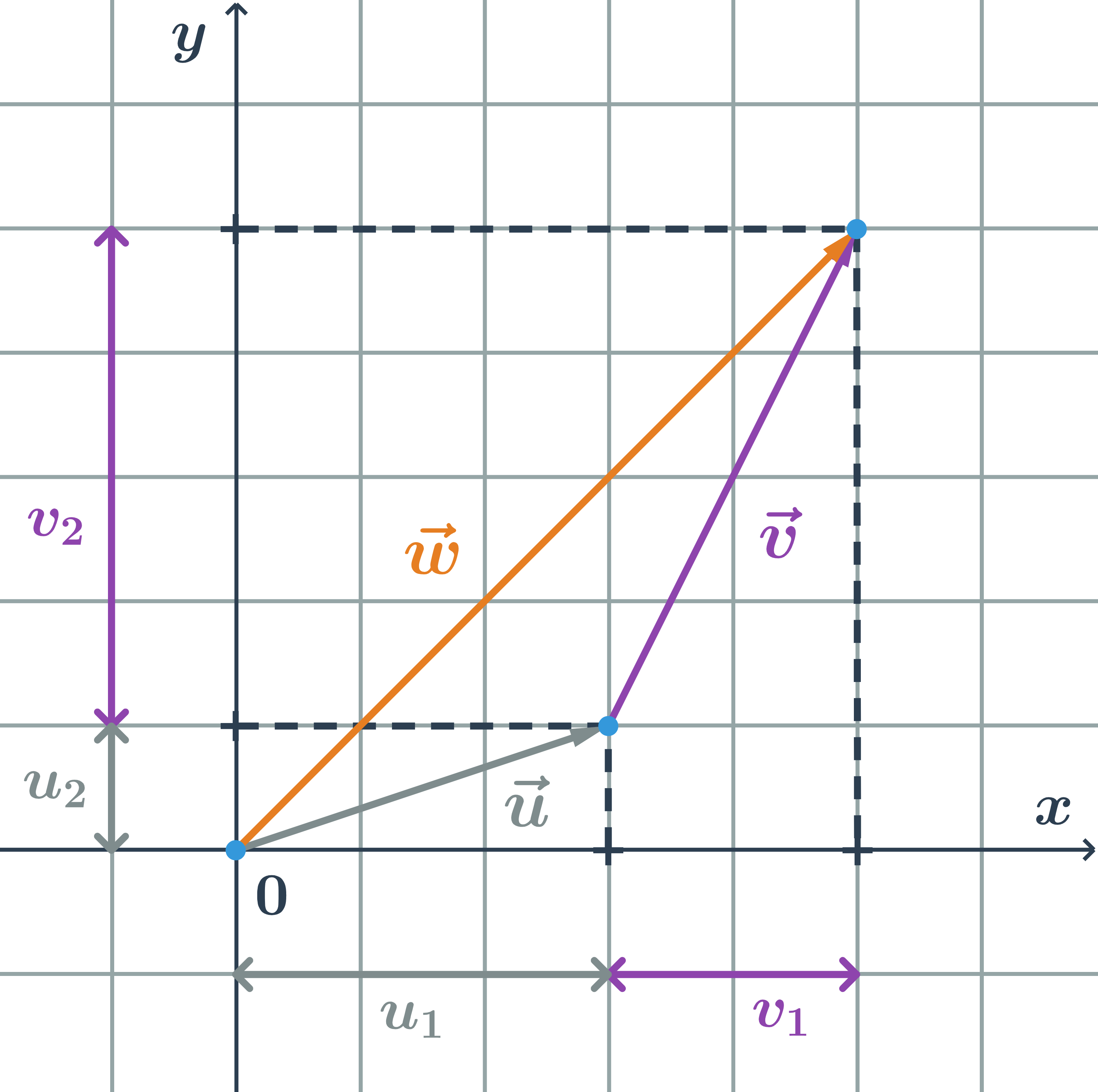
Majme vektory so súradnicami \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2). Potom súčet vektorov \vec{u} a \vec{v} je vektor \vec{w} so súradnicami \vec{w}=(u_1+v_1; u_2+v_2).
Rozdiel vektorov
Rozdiel vektorov \vec{u} a \vec{v} je súčet vektora \vec{u} s vektorom opačným k \vec{v}. Teda:
\vec{u}-\vec{v}=\vec{u}+(-\vec{v})
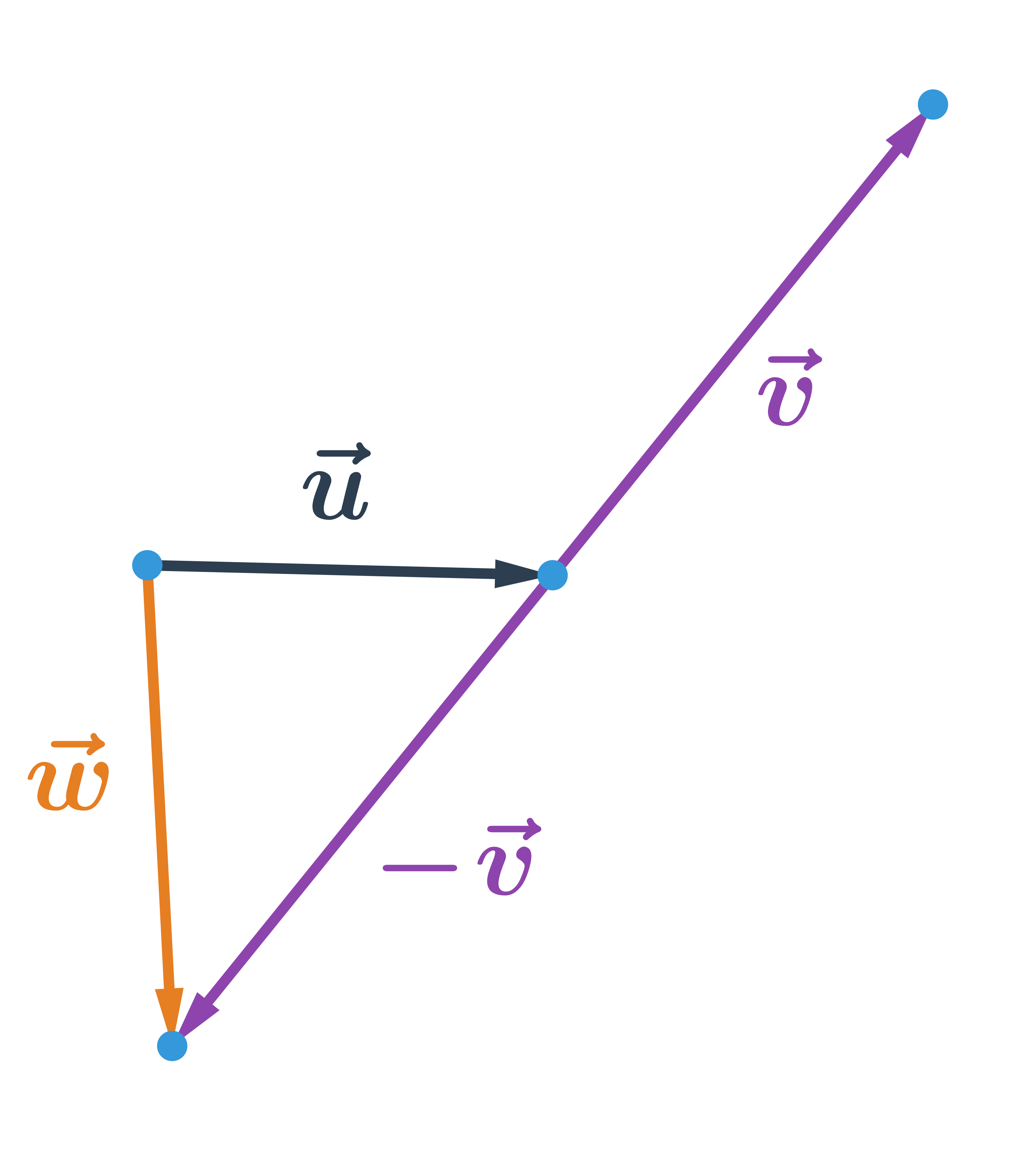
Ak máme súradnice vektorov: \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), potom rozdiel vektorov \vec{u} a \vec{v} je vektor \vec{w}, ktorý má súradnice: \vec{w}=(u_1-v_1; u_2-v_2).
Násobok vektora
Vektor \vec{u} môžeme vynásobiť ľubovoľným reálnym číslom k. Dostaneme vektor \vec{v}, ktorému hovoríme násobok vektora. Píšeme \vec{v}=k \cdot \vec{u}
- Ak k > 0, vektory \vec{u} a k \cdot \vec{u} majú rovnaký smer
- Ak k < 0, vektory \vec{u} a k \cdot \vec{u} majú opačný smer
- Ak k = 0, vektor k \cdot \vec{u} je nulový vektor
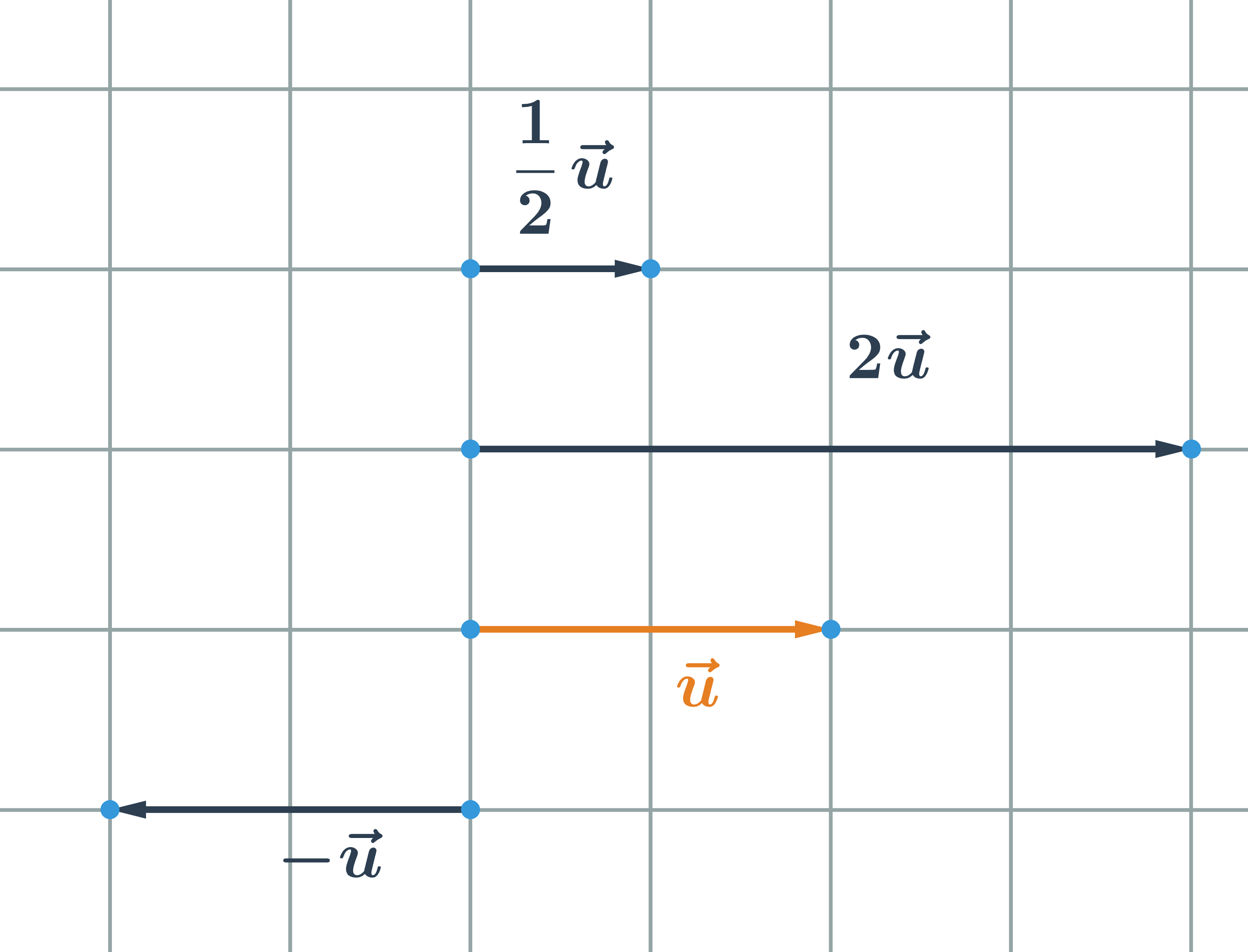
Ak máme súradnice vektora \vec{u}=(u_1;u_2), potom jeho násobok \vec{v}=k \cdot \vec{u} má súradnice \vec{v}=(k \cdot u_1; k\cdot u_2).
Príklad súčtu a násobku vektora graficky
Načrtnite vektor \vec{w}=2\vec{a}-\vec{b}+\vec{c}.
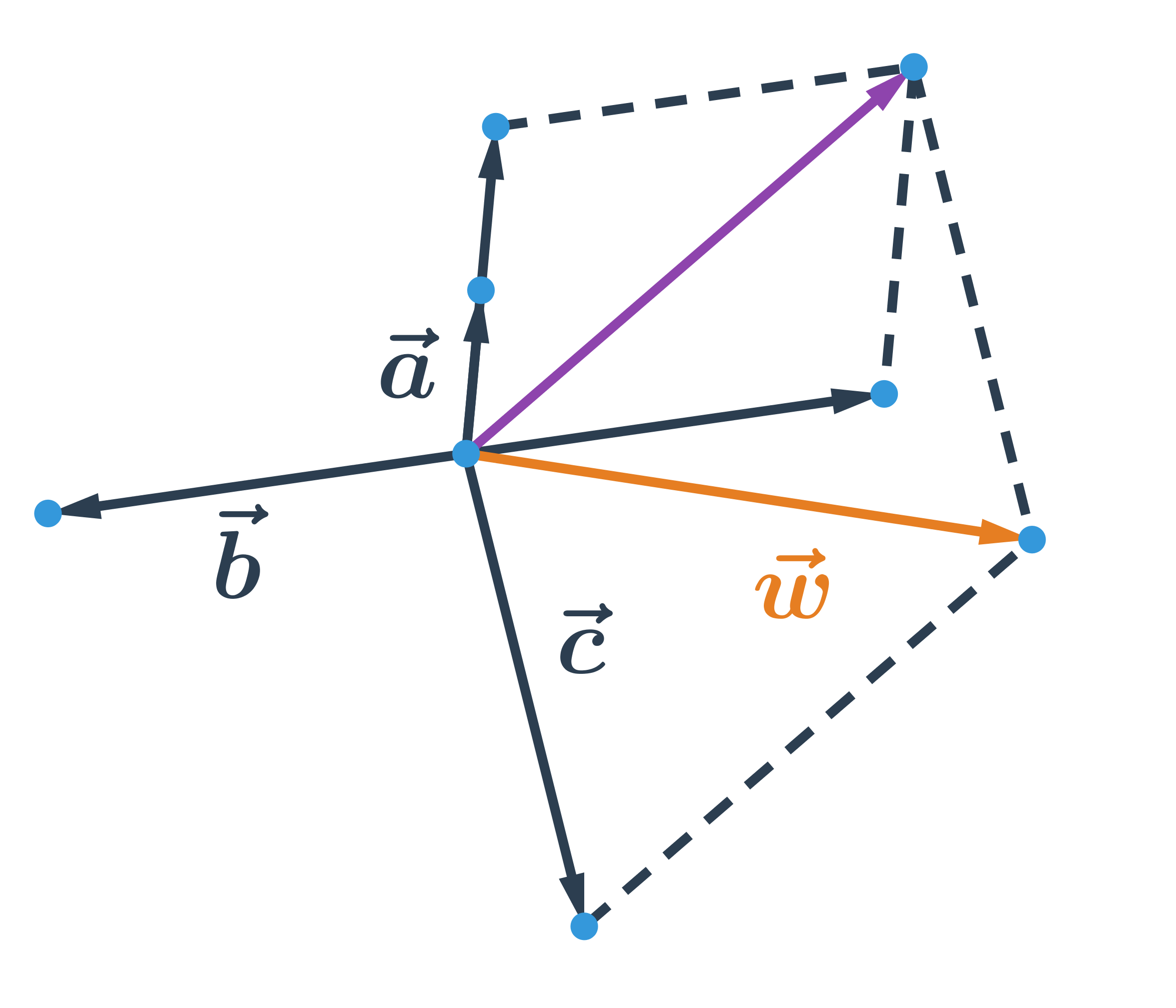
Príklad súčtu a násobku vektora v súradniciach
Sú dané vektory \vec{u}=(2;-3), \vec{v}=(4;1). Určite súradnice vektora \vec{w}=\vec{u}-4\cdot \vec{v}.
- w_1=u_1-4\cdot v_1=2-4\cdot 4=-14
- w_2=u_2-4\cdot v_2=-3-4\cdot 1=-7
Zatvoriť














