Aritmetika
Číselná os do 20
Číselná os znázorňuje čísla. Čísla sú na nej vyznačené značkami. Popísané sú väčšinou len niektoré značky, inak by sa popisky prekrývali a bolo by to neprehľadné. Zvyšné čísla si dopočítame. Číselnú os si môžeme predstaviť ako prechádzku. Začíname na štarte, ktorým je číslo nula, a každý krok vedie na novú značku s novým číslom.
Jednoduchý príklad číselnej osi, na ktorej hľadáme číslo 7:

Rímske číslice
Rímske číslice predstavujú spôsob zápisu čísel pomocou písmen latinskej abecedy. Na rozdiel od bežne používaného zápisu čísel (arabské číslice, desiatková sústava) ide o nepozičnú číselnú sústavu. Rímske číslice nie sú vhodné pre matematické výpočty, napríklad násobenie v tomto zápise je výrazne náročnejšie než v desiatkovej sústave. Rímske číslice sa však stále používajú, napríklad pre uvádzanie letopočtov na pamätníkoch, na hodinách, pre číslovanie kapitol v knihách, …
Základné rímske číslice sú I, V, X, L, C, D, M. Ich hodnoty sú nasledujúce:
| I | V | X | L | C | D | M |
|---|---|---|---|---|---|---|
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Ďalšie čísla vytvárame spojovaním a opakovaním symbolov. Symboly radíme za seba podľa veľkosti. Na skrátenie zápisu sa využíva odčítanie v prípade, že menší symbol predchádza väčšiemu. Príklady:
| Rímske | Desiatkové | Vysvetlenie |
|---|---|---|
| XXVII | 27 | jednoduché sčítanie príslušných symbolov: 10 + 10 + 5 + 1 + 1 |
| MDCCXIII | 1713 | zase jednoduché sčítanie príslušných symbolov: 1000 + 500 + 100 + 100 + 10 + 1 + 1 + 1 |
| IV | 4 | I je pred V, odčítame teda: -1 + 5 |
| XIX | 19 | I je pred X, zase odčítame: 10 - 1 + 10 |
| DCCXC | 790 | X je pred C, odčítame teda 10: 500 + 100 + 100 - 10 + 100 |
Zaokrúhlovanie na desiatky a stovky
Zaokrúhlovanie znamená, že vezmeme číslo a nahradíme ho za iné, ktoré má približne rovnakú veľkosť, ale je „jednoduchšie“. Napríklad číslo 96 môžeme zaokrúhliť na číslo 100. Zaokrúhlovanie nám umožňuje napríklad vykonávať približné výpočty alebo ľahšie komunikovať.
Zaokrúhlovanie na desiatky znamená, že číslo nahradíme najbližším násobkom desiatky. Napríklad k číslu 37 je najbližší násobok desiatky číslo 40 (má vzdialenosť 3). Pri číslach, ktoré sa končia cifrou 5, nie je takto definované zaokrúhlovanie jednoznačné, napríklad číslo 35 má rovnakú vzdialenosť od čísel 30 a 40. Pre tieto prípady je zavedené pravidlo, ktoré hovorí, že zaokrúhlujeme nahor, teda číslo 35 zaokrúhlujeme na 40. Zaokrúhlovanie na stovky funguje rovnako, len nahradzujeme číslo najbližším násobkom stovky. Príklady:
44 zaokrúhlené na desiatky je 40.
47 zaokrúhlené na desiatky je 50.
165 zaokrúhlené na desiatky je 170.
30 zaokrúhlené na desiatky je 30 (číslo 30 už je násobok desiatky, tak ho jednoducho necháme tak).
487 zaokrúhlené na stovky je 500.
1842 zaokrúhlené na stovky je 1800.
850 zaokrúhlené na stovky je 900.
1111 zaokrúhlené na stovky je 1100.
Sčítanie pod sebou
Pri písomnom sčítaní postupujeme nasledovne:
- Čísla si napíšeme pod seba, zarovnané doprava.
- Postupujeme z pravej strany.
- Vždy sčítame dve čísla pod sebou a výsledok zapíšeme pod ne.
- Ak je výsledok väčší než 10, zapisujeme len číslo na pozícii jednotiek. Číslo na pozícii desiatok prenášame ďalej doľava – pripočítame ho v ďalšom stĺpci.
Príklad 3728+436:
- Postupujeme sprava, teda najskôr sčítame 8+6=14. Zapisujeme 4, 1 prenášame ďalej.
- Ďalej sčítame 2+3 a ešte pripočítame 1 z predchádzajúceho stĺpca. Zapisujeme 6.
- Ďalej sčítame 7+4=11 (z predchádzajúceho stĺpca nič neprenášame), zapisujeme 1 a 1 prenášame.
- Ďalej už máme len 3, z druhého čísla nám nič nezostalo. Pridáme však ešte 1 z predchádzajúceho stĺpca. Zapisujeme 4.
- Dostávame výsledok 4164.
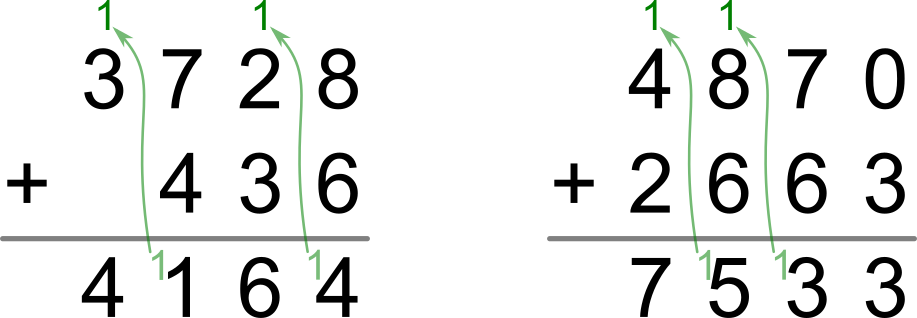
Odčítanie pod sebou
Pri písomnom odčítaní postupujeme nasledovne:
- Čísla si napíšeme pod seba, zarovnané doprava.
- Postupujeme z pravej strany.
- Vždy odčítame dve čísla pod sebou a výsledok zapíšeme pod ne.
- Ak je horné číslo menšie než spodné, tak si „požičiame“ desiatku a namiesto nej v ďalšom stĺpci odčítame o 1 viac.
Príklad 3728-436:
- Postupujeme sprava, teda najskôr odčítame 8-6=2.
- V ďalšom stĺpci odčítame 2-3. Tu je 2 menšia než 3, „požičiame“ si desiatku a počítame 12-3=9.
- Ďalej odčítame 7-4, musíme ale ešte odčítať 1 za požičanú desiatku z predchádzajúceho stĺpca, teda 7-4-1=2.*
- V ďalšom stĺpci už máme len 3, od nej nemáme čo odčítať.
- Výsledok je teda 3292.
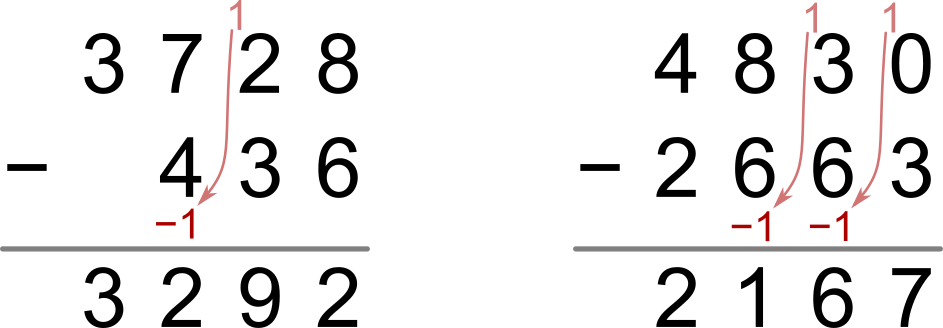
Malá násobilka
Násobenie nám hovorí, koľko štvorčekov má čokoláda, keď vieme, koľko má riadkov a stĺpcov:
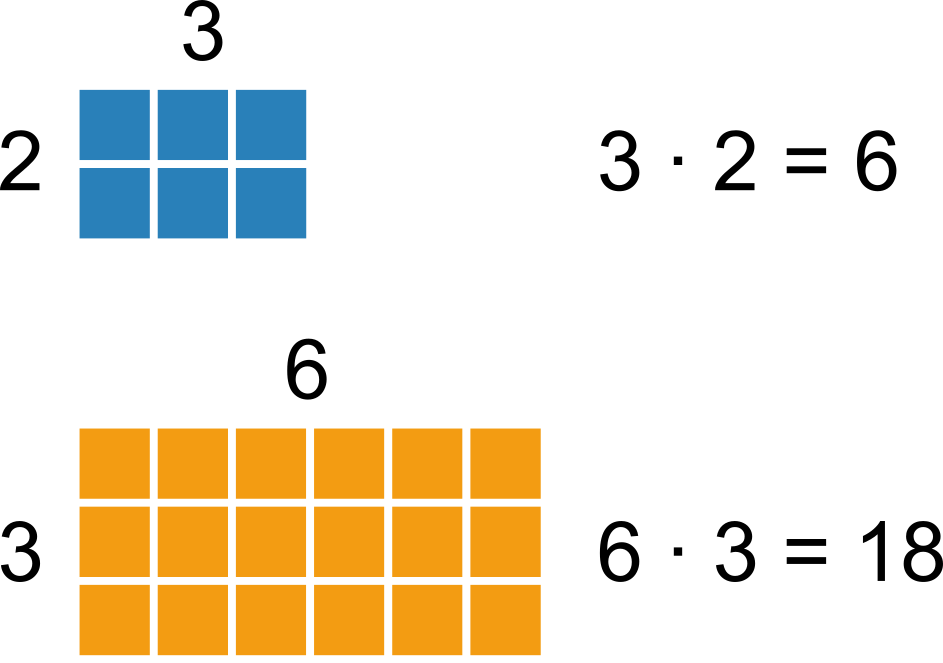
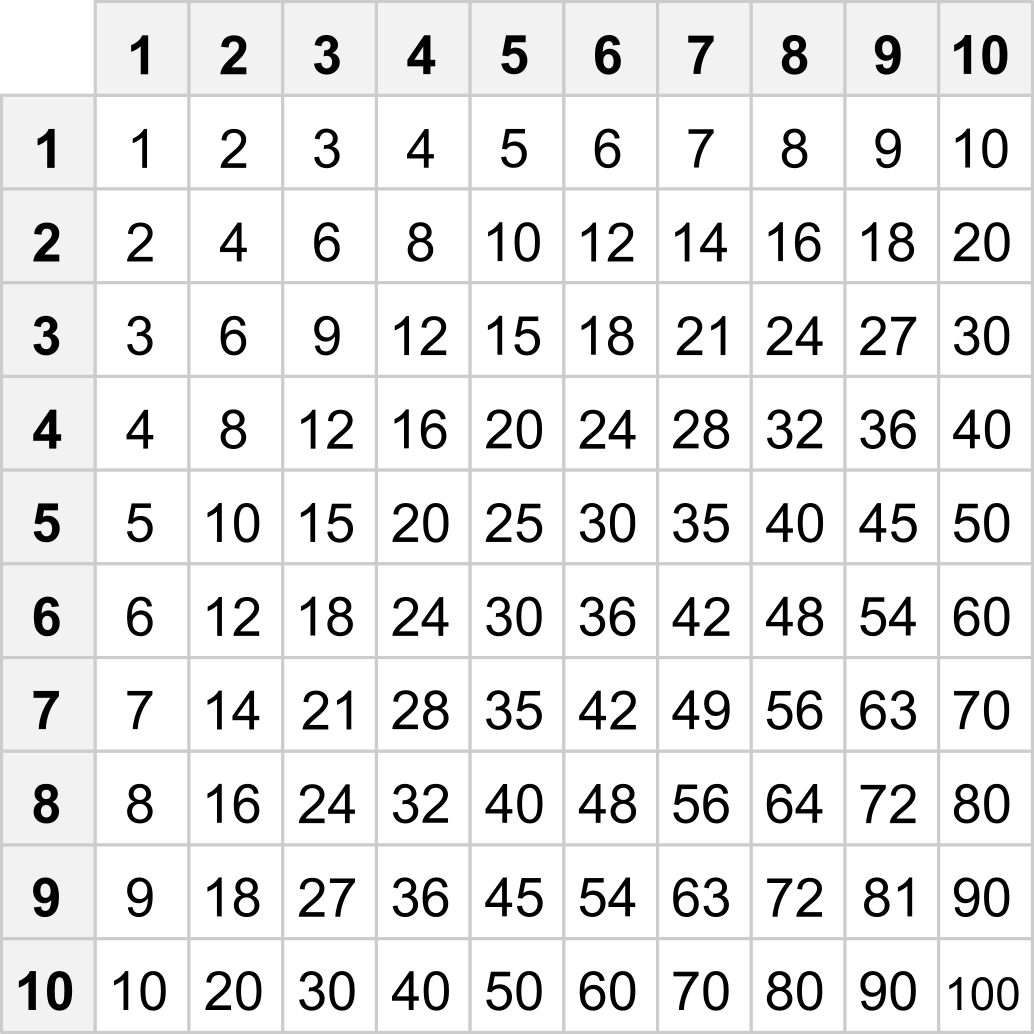
Násobenie využívame v matematike a aj v bežnom životě veľmi často. Preto sa skutočne oplatí naučiť sa základné násobky naspamäť. Malá násobilka zahŕňa vzájomné súčiny čísel od 1 do 10. Tie môžeme prehľadne vyjadriť tabuľkou malej násobilky:
Písomné násobenie pod sebou
Pri písomnom násobení postupujeme nasledujúco:
- Čísla si napíšeme pod seba, zarovnané doprava.
- Postupne jednotlivými ciframi spodného čísla vynásobíme celé horné číslo.
- Výsledky jednotlivých násobení zapisujeme na riadky pod seba. Výsledky odsadzujeme podľa pozície cifry, ktorú sme násobili.
- Nakoniec všetky jednotlivé výsledky sčítame (viď postup pre sčítanie pod sebou).
Obrázok ukazuje príklad násobenia čísel 79 a 68.

Jednociferné delenie
Keď mám 8 jabĺčok a chcem ich rozdeliť rovnomerne do 4 košíkov, koľko jabĺčok bude v každom košíku? Túto otázku nám v matematike pomôže vyriešiť delenie:
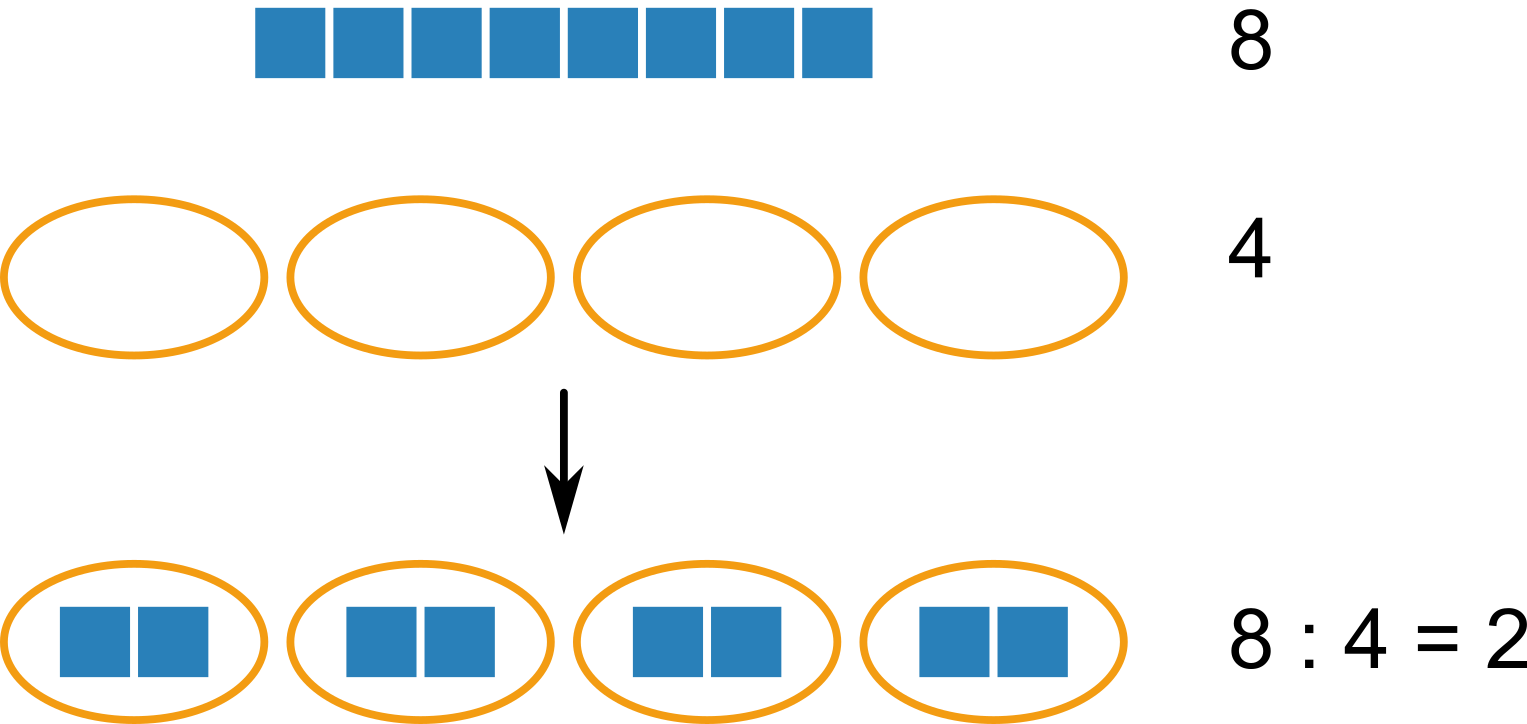
Delenie so zvyškom
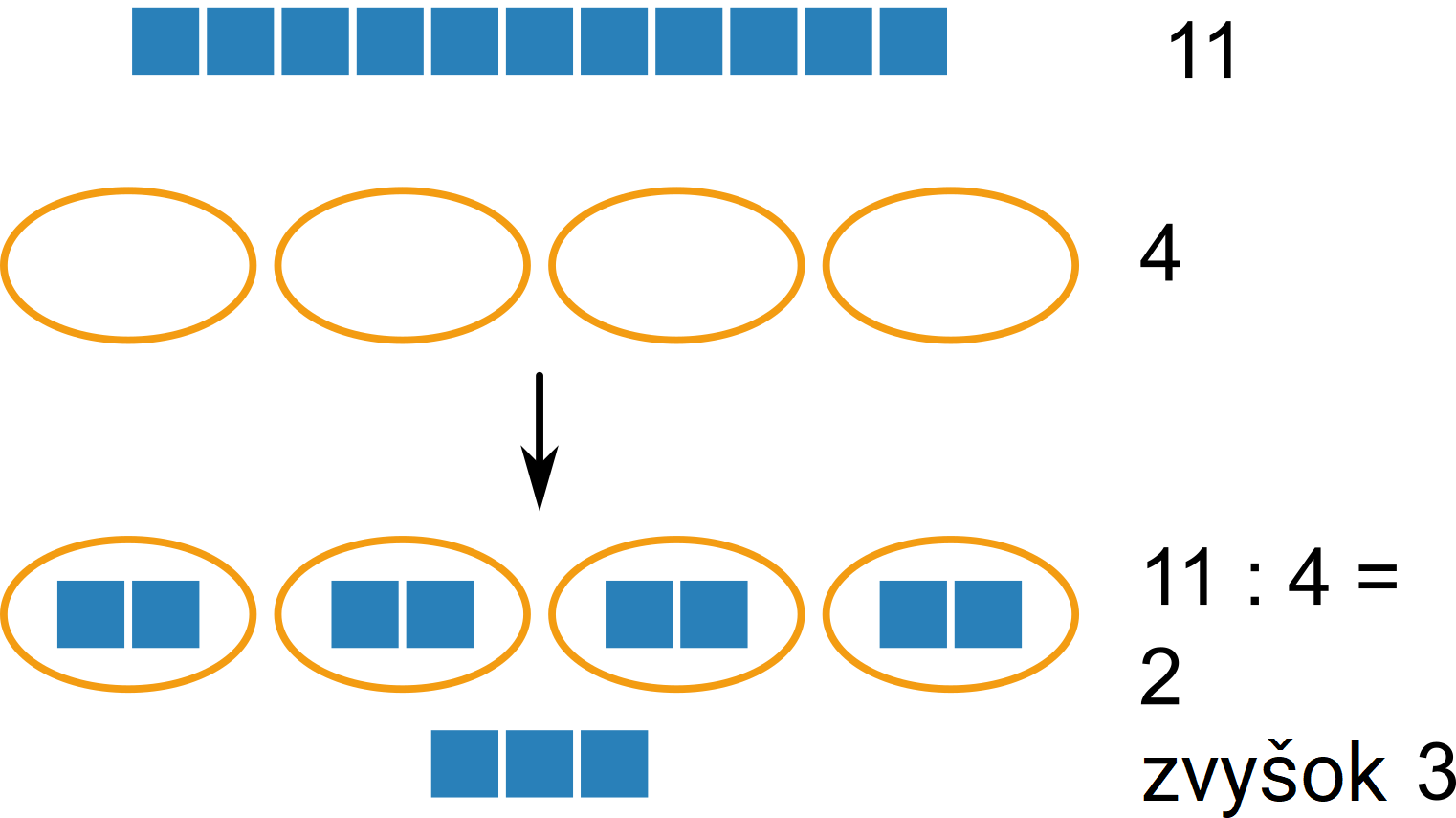
Zvyšok súvisí s celočíselným delením. Ak delíme a:b, potom môžeme písať a = k\cdot b + z, pričom 0 \leq z < b. Číslo k nazýváme podiel, číslo z zvyšok. Operácia delenie so zvyškom sa v matematike nazýva tiež modulo.
Príklad: 11:4 dáva podiel 2 a zvyšok 3, pretože 11 = 2\cdot 4 + 3. Keď mám 11 jabĺk a rozdelím ich rovnomerne do 4 košíkov, v každom košíku budú 2 jablká a ešte mi 3 zostanú.
Ďalšie príklady:
- 17:5 dáva zvyšok 2, pretože 17 = 3\cdot 5 + 2.
- 21:6 dáva zvyšok 3, pretože 21 = 3\cdot 6 + 3.
- 12:7 dáva zvyšok 5, pretože 12 = 1\cdot 7 + 5.
- 4:6 dáva zvyšok 4, pretože 4 = 0\cdot 6 + 4.
Poradie operácií, zátvorky
Výrazy vyhodnocujeme v tomto poradí:
- zátvorky,
- násobenie a delenie,
- sčítanie a odčítanie.
Príklady:
| 1+ 2\cdot 3 + 4 | = 1+ 6+4=11 | Najskôr násobenie, potom sčítanie. |
| (1+2)\cdot 3 +4 | = 3\cdot 3 +4 = 9 + 4 = 13 | Najskôr zátvorka, potom násobenie, nakoniec sčítanie. |
| (1+2)\cdot(3 +4) | = 3\cdot 7 = 21 | Najskôr obe zátvorky, potom násobenie. |
Číselná os: celé čísla
Číselná os je priamka znázorňujúca čísla. Značkami sú na nej vyznačené vybrané, väčšinou celé, čísla. Popísané sú väčšinou len niektoré značky, inak by sa popisky prekrývali a bolo by to neprehľadné. Zvyšné čísla si dopočítame.
Tradične sa na číselnej osi píšu menšie čísla vľavo, väčšie čísla vpravo. Záporné čísla sú teda vľavo od nuly. Príklad číselnej osi s vyznačenými hodnotami 7 a -7:

Počítanie so zápornými číslami
Pri počítaní so zápornými číslami často používame princíp „mínus a mínus dáva plus“. Konkrétne príklady:
| Pričítanie záporného čísla je to isté ako odčítanie: | 6 + (-2) = 6-2=4 |
| Odčítanie záporného čísla sa upraví na pričítanie: | 6 - (-2) = 6+2=8 |
| Násobenie kladného a záporného čísla dá záporný výsledok: | 6\cdot(-2) = -12 |
| Násobenie dvoch záporných čísel dá kladný výsledok: | (-6)\cdot(-2) = 12 |
| Delenie kladného čísla záporným dá záporný výsledok: | 6:(-2) = -3 |
| Delenie záporného čísla záporným dá kladný výsledok: | (-6):(-2) = 3 |
Výrazy s absolútnou hodnotou
Absolútna hodnota čísla je jeho vzdialenosť od nuly. Absolútnu hodnotu čísla x značíme pomocou zvislých čiar: |x|. Pre kladné x je |x|=x, pre záporné x je |x| = -x. Príklady:
- |5| = 5
- |-5| = 5
- |-13| = 13
- |2{,}45| = 2{,}45
Pri vyhodnocovaní výrazov, v ktorých sa vyskytuje absolútna hodnota, najskôr vyhodnotíme výraz vnútri zvislých čiar (podobne ako pri zátvorkách) a potom aplikujeme samotnú absolútnu hodnotu:
- 3 + |4-6| = 3 + |-2| = 3+2=5
- 5-3 \cdot |4-2| = 5 -3\cdot|2| = 5 -3\cdot2 = 5 - 6 = -1
Dávame si pozor na rozdiel medzi obyčajnou zátvorkou (ktorá len vyznačuje prednosť operácií) a zvislými čiarami (ktoré značia absolútnu hodnotu):
- 3+(-2) = 3 - 2 = 1
- 3+|-2| = 3 + 2 = 5
Tiež si dávame dobrý pozor, kde sa vyskytujú znamienka mínus (pred verzus za zvislou čiarou):
- |-4| = 4
- -|4| = -4
- |-3-2| = |-5| = 5
- -|3-2| = -|1| = -1
Deliteľnosť
Deliteľnosť sa zaoberá určovaním, či je jedno číslo deliteľné druhým bez zvyšku. Napríklad číslo 24 je deliteľné číslom 6, ale nie je deliteľné číslom 7.
Párnosť a nepárnosť zodpovedá deliteľnosti číslom 2, ide o najjednoduchší prípad deliteľnosti.
Podmienky deliteľnosti nám pomáhajú určiť, či je jedno číslo deliteľné iným číslom bez toho, aby sme vykonávali samotné delenie. Napríklad číslo je deliteľné 3, ak je jeho ciferný súčet deliteľný 3. Aby sme teda zistili, že číslo 513 je deliteľné číslom 3, stačí si všimnúť, že ciferný súčet (5+1+3=9) je deliteľný 3 a nemusíme vykonávať delenie 513:3.
Prvočísla sú čísla väčšie než 1, ktoré majú iba dva delitele: jednotku a seba samého. Prvočísla sú základnými stavebnými kameňmi ostatných čísel v zmysle ich deliteľnosti.
Najväčší spoločný deliteľ je najväčšie číslo, ktorým sú dve alebo viac čísel bezo zvyšku deliteľné. Spoločný deliteľ hrá kľúčovú rolu pri zjednodušovaní zlomkov a riešení rovníc.
Najmenší spoločný násobok je najmenšie číslo, ktoré je násobkom dvoch alebo viac čísel. Spoločný násobok sa často používa pri práci so zlomkami.
Deliteľnosť je základom pre veľa konceptov v matematike a má bohaté využitie napríklad v modernej kryptológii (šifrovanie).
Párne, nepárne
Párne čísla sú celé čísla, ktorá sú bez zvyšku deliteľné dvomi. Párne čísla sa končia cifrou 0, 2, 4, 6 alebo 8. Príklady párnych čísel sú 138, 12, 0, 9356, -34, 6.
Nepárne čísla sú celé čísla, ktoré majú po delení dvomi zvyšok jedna. Nepárne čísla sa končia cifrou 1, 3, 5, 7 alebo 9. Príklady nepárnych čísel sú 15, 891, -7, 1, 95.
Deliteľnosť
Číslo a je deliteľné nenulovým celým číslom b práve vtedy, keď je a celočíselným násobkom b, tj. a = k\cdot b. Inými slovami: číslo a dáva po delení číslom b zvyšok 0. Príklady:
- Číslo 15 je deliteľné číslom 5, pretože 15 = 3\cdot 5.
- Číslo 25 nie je deliteľné číslom 4, pretože 25 = 6\cdot 4 + 1 (zvyšok nie je nulový).
Pre niektoré delitele môžeme deliteľnosť rozoznať pomerne ľahko:
| Deliteľ | Kritérium | Príklady |
|---|---|---|
| 2 | Párne číslo na mieste jednotiek. | 18, 2546, 27781452 |
| 3 | Ciferný súčet deliteľný číslom 3. | 252867 (2+5+2+8+6+7=30) |
| 4 | Posledné dvojčíslie je deliteľné číslom 4. | 180, 73524 |
| 5 | Na mieste jednotiek je 0 alebo 5. | 90, 1265 |
| 9 | Ciferný súčet deliteľný číslom 9. | 252864 (2+5+2+8+6+4=27) |
| 10 | Na mieste jednotiek je 0. | 250, 18763520 |
Prvočísla
Prvočíslo je prirodzené číslo väčšie než 1, ktoré je deliteľné len jednotkou a sebou samým.
Zložené číslo je prirodzené číslo väčšie než 1, ktoré nie je prvočíslom, má teda aj iný deliteľ než jednotku a seba samého.
Príklady:
- 6 je zložené číslo, pretože je deliteľné napríklad číslom 2.
- 7 je prvočíslo, pretože je deliteľné len číslami 1 a 7.
- 13 je prvočíslo, pretože je deliteľné len číslami 1 a 13.
- 15 je zložené číslo, pretože je deliteľné napríklad číslom 3.
Podľa vyššie uvedenej definície nie je číslo 1 prvočíslo ani zložené číslo. Taká je bežná matematická konvencia, pretože to vedie k elegantnejšej formulácii rôznych matematických výsledkov. Existujú ale aj iné prístupy k poňatiu prvočíselnosti jednotky (historické).
Prvočísel je nekonečne veľa. Prvočísla menšie než 100 sú: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Každé číslo sa dá jednoznačne rozložiť na prvočíselný rozklad, napr.:
- 12 = 2 \cdot 2 \cdot 3
- 30 = 2 \cdot 3\cdot 5
- 1638 = 2 \cdot 3^2\cdot 7\cdot 13
Najväčší spoločný deliteľ
Najväčší spoločný deliteľ (NSD) dvoch celých čísel je najväčšie číslo, ktoré bez zvyšku delí obe čísla. Príklady: NSD(18, 24) = 6, NSD(12, 21) = 3, NSD(24, 35) = 1. Najväčší spoločný deliteľ je možné zovšebecniť aj na väčší počet vstupných čísel. Napríklad NSD(30, 85, 90) = 5. Typickým využitím najväčšieho spoločného deliteľa je krátenie zlomkov. Ak je najväčší spoločný deliteľ dvoch čísel 1, nazývame ich nesúdeliteľné. Napríklad čísla 15 a 32 sú nesúdeliteľné.
V prípade malých čísel môžeme najväčší spoločný deliteľ určiť tak, že si jednoducho vypíšeme všetky delitele. Ak hľadáme NSD(18, 24) postupujeme takto:
- Delitele čísla 18 sú 1, 2, 3, 6, 9, 18.
- Delitele čísla 24 sú 1, 2, 3, 4, 6, 8, 12, 24.
- Spoločné delitele čísel 18 a 24 sú 1, 2, 3, 6.
- Najväčší spoločný deliteľ je 6.
Pri väčších číslach môžeme najväčší spoločný deliteľ určiť pomocou prvočíselného rozkladu. Obe čísla rozpíšeme ako súčin prvočísel, výsledný NSD je súčin prvočísel vyskytujúcich sa v oboch rozkladoch umocnených na príslušné najmenšie exponenty.
- Príklad \mathit{NSD}(18, 24):
- 18 = 2\cdot 3 \cdot 3 = 2\cdot3^2
- 24 = 2 \cdot 2 \cdot 2\cdot 3 = 2^3\cdot 3
- Spoločná časť prvočíselného rozkladu: 2, 3.
- \mathit{NSD}(90, 168) = 2\cdot 3 = 6
- Príklad \mathit{NSD}(540, 315):
- 540 = 2\cdot 2\cdot3\cdot 3\cdot 3\cdot 5 = 2^2\cdot3^3\cdot 5
- 315 = 3\cdot 3 \cdot 5\cdot 7 = 3^2 \cdot 5\cdot 7
- Spoločná časť prvočíselného rozkladu: 3, 3, 5
- \mathit{NSD}(540, 315) = 3\cdot 3\cdot 5 = 3^2\cdot 5 = 45
Pre praktické výpočty sa používajú iné algoritmy, hlavne Euklidov algoritmus.
Najmenší spoločný násobok
Najmenší spoločný násobok (NSN) dvoch celých čísel je najmenšie číslo, ktoré je bez zvyšku deliteľné obomi číslami. Príklady: NSN(12, 15) = 60, NSN(6, 8) = 24, NSN(3, 15) = 15. Pojem najmenšieho spoločného násobku je možné zovšebecniť aj na väčší počet vstupných čísel. Napríklad NSN(2, 3, 4) = 12. Typické využitie najmenšieho spoločného násobku je pri prevode zlomkov na spoločný menovateľ pri sčítaní zlomkov.
Pre malé čísla môžeme najmenší spoločný násobok nájsť tak, že si vypíšeme niekoľko prvých násobkov od oboch čísel. ak hľadáme NSN(12, 15), postupujeme takto:
- Násobky čísla 12 sú 12, 24, 36, 48, 60, 72, 84, …
- Násobky čísla 15 sú 15, 30, 45, 60, 75, 90, …
- Najmenší spoločný násobok je prvé číslo, ktoré sa vyskytuje v oboch zoznamoch. V tomto prípade teda 60.
V prípade väčších čísel môžeme najmenší spoločný násobok nájsť pomocou prvočíselného rozkladu. NSN sa rovná súčinu všetkých prvočísel, ktoré sa vyskytujú aspoň v jednom rozklade (v najvyššej mocnine, v akej sa vyskytujú).
Príklad \mathit{NSN}(24, 45):
- 24 = 2^3\cdot 3
- 45 = 3^2 \cdot 5
- \mathit{NSN}(24, 45) = 2^3 \cdot 3^2 \cdot 5 = 360
Najmenší spoločný násobok sa tiež dá vypočítať pomocou najväčšieho spoločného deliteľa (NSD): \mathit{NSN}(a, b) = \frac{a\cdot b}{\mathit{NSD}(a, b)}
Mocniny, odmocniny, logaritmy
Umocňovanie je opakované násobenie. Napríklad 3^5 = 3\cdot 3\cdot 3\cdot 3\cdot 3 = 243. Odmocňovanie je opačnou operáciou k umocňovaniu. Napríklad druhá odmocnina z 36 je 6 (\sqrt{36}=6), pretože 6^2 = 6\cdot 6 = 36. Mocniny a odmocniny využívame v mnohých oblastiach matematiky, napríklad pri práci s mnohočlenmi, riešení kvadratických rovníc, výpočte obsahu a objemu alebo pri určovaní dĺžok strán v trojuholníku.
Prvým krokom pre zvládnutie tejto témy sú základné mocniny a odmocniny, kde pracujeme s malými, prirodzenými číslami. Pre tieto čísla sa vyplatí sa naučiť základné mocniny a odmocniny naspamäť, pretože na ne často v matematike narazíme.
Ako ďalší krok potrebujeme zvládnuť pracovať s výrazmi s mocninami a odmocninami.
Umocňovanie je možné definovať aj pre záporný mocniteľ. Tento spôsob umocňovania sa využíva na vedecký zápis čísel, ktorý nám umožňuje prehľadne pracovať s veľmi veľkými alebo veľmi malými číslami, vďaka čomu má hojné využitie vo fyzike.
Umocňovanie a odmocňovanie môžeme prirodzene používať aj v spojitosti so zlomkami a desatinnými číslami.
Mocniny sú skráteným zápisom opakujúceho sa násobenia. Príklady:
- 3^2 = 3\cdot 3 = 9
- 2^3 = 2\cdot 2 \cdot 2= 8
- 5^4 = 5\cdot 5\cdot 5\cdot 5 = 625
Pri umocňovaní záporných čísel je výsledok kladný pre párne mocniny, záporný pro nepárne mocniny.
- (-3)^2 = (-3)\cdot (-3) = 9
- (-3)^3 = (-3)\cdot (-3)\cdot (-3) = -27
- (-3)^4 = (-3)\cdot (-3)\cdot (-3)\cdot (-3) = 81
Nultá mocnina akéhokoľvek čísla je 1 (napr. 5^0=1, 564^0=1). Nula umocnená na ľubovoľné číslo je 0 (napr. 0^3 = 0\cdot 0\cdot 0 = 0). Čo poukazuje na zaujímavú otázku: Čomu sa rovná 0^0?
Odmocniny
Odmocňovanie v matematike je čiastočne inverznou (opačnou) operáciou k umocňovaniu. Druhá odmocnina z čísla x je také nezáporné číslo a, pre ktoré platí a^2 = x. Druhú odmocninu značíme \sqrt{x}. Príklady:
- \sqrt{9} = 3, pretože 3^2 = 9
- \sqrt{25} = 5, pretože 5^2 = 25
- \sqrt{100} = 10, pretože 10^2 = 100
Všeobecne potom n-tá odmocnina z x je také číslo a, pre ktoré platí a^n = x, n-tú odmocninu značíme \sqrt[n]{x}. Príklady:
- \sqrt[3]{125} = 5, pretože 5^3 = 25
- \sqrt[5]{32} = 2, pretože 2^5 = 32
- \sqrt[4]{10000} = 10, pretože 10^4 = 10000
Odmocňovanie má aj geometrický význam. Ak máme štvorec s obsahom S, potom má tento štvorec dĺžku strany rovnú druhej odmocnine \sqrt{S}. Ak máme kocku s objemom V, potom má táto kocka dĺžku hrany rovnú tretej odmocnine \sqrt[3]{V}. Odmocniny často využijeme napríklad pri aplikácii Pytagorovej vety.
Graf funkcie odmocnina
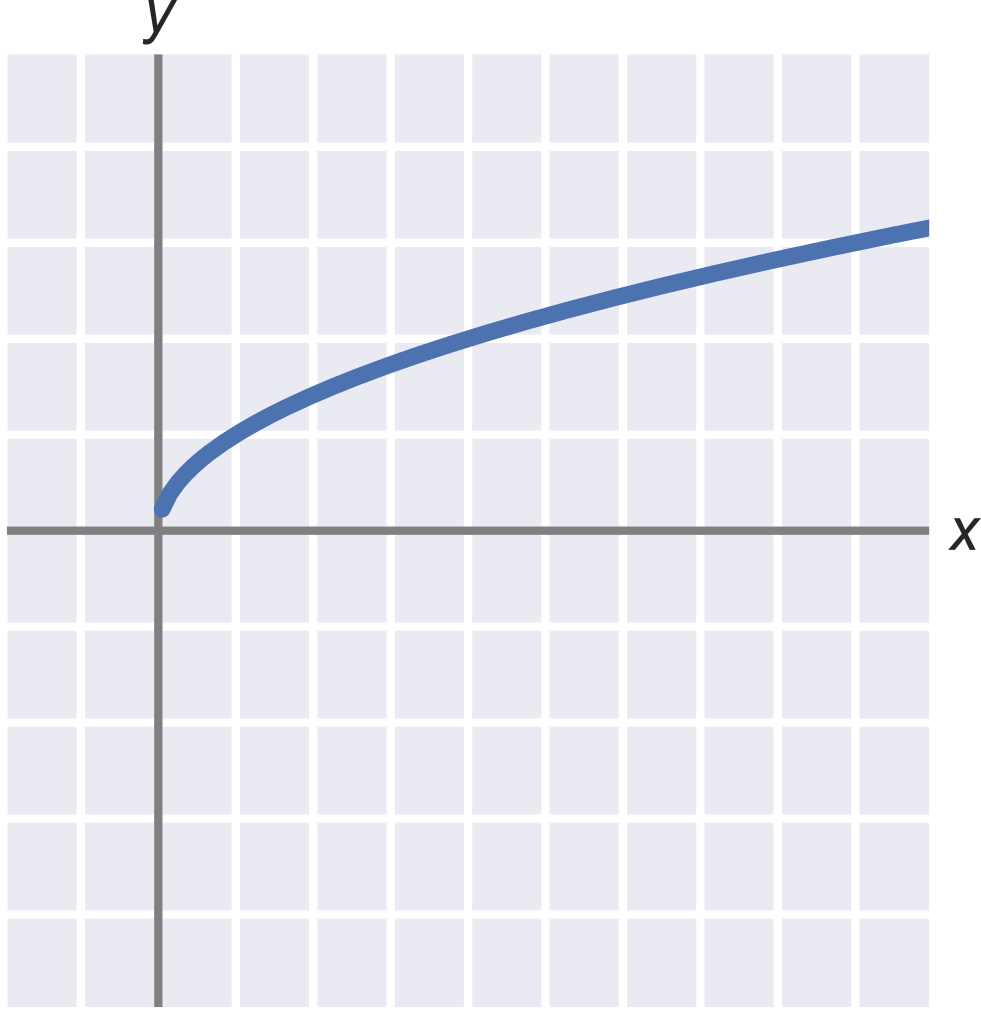
Odmocnina a záporné čísla
Keď hľadáme odmocninu napríklad z 25, tak hľadáme číslo, ktoré po umocnení dá 25. To spĺňa 5\cdot 5, ale tiež (-5)\cdot (-5). Odmocnina je však definovaná ako nezáporné číslo, takže \sqrt{25} = 5.
Druhú odmocninu môžeme počítať len z kladných čísel, pretože akékoľvek číslo umocnené na druhú je kladné. Odmocnina zo záporných čísel nie je definovaná. Alebo vlastne je, ale to musíme zaviesť komplexné čísla (čo je veľmi zaujímavý a užitočný nástroj, ale už trochu pokročilý, takže ho tu nebudeme rozoberať).
Pre bežné reálne čísla môžeme počítať odmocniny zo záporných čísel pre nepárne stupne n. Napríklad:
- \sqrt[3]{-8} = -2, pretože (-2)^3 = -8
- \sqrt[5]{-100000} = -10, pretože (-10)^5 = -100000
Výrazy s mocninami a odmocninami
Pre mocniny platia nasledujúce vzťahy:
- x^0 = 1
- x^a \cdot x^b = x^{a+b}
- x^a : x^b = x^{a-b}
- (x^a)^b = x^{a\cdot b}
- (x\cdot y)^a = x^a\cdot y^a
Konkrétne príklady, ktoré názorne ilustrujú, prečo uvedené vzťahy platia:
- 7^3\cdot 7^2 = (7\cdot 7\cdot7) \cdot (7\cdot 7) = 7^{3+2} = 7^5
- 6^4: 6^2 = (6\cdot 6\cdot 6\cdot 6) : (6\cdot 6) = 6^{4-2} = 6^2
- (5^3)^2 = (5\cdot 5\cdot 5)^2 = (5\cdot 5\cdot 5) \cdot (5\cdot 5\cdot 5) = 5^{3\cdot 2} = 5^6
- (7\cdot 8)^3 = (7\cdot 8) \cdot (7\cdot 8) \cdot (7\cdot 8) = (7\cdot 7\cdot 7) \cdot (8\cdot 8\cdot 8) = 7^3 \cdot 8^3
Pre odmocniny platia nasledujúce vzťahy (predpokladáme x, y > 0):
- \sqrt{0} = 0
- \sqrt{1} = 1
- \sqrt{x}\cdot \sqrt{x} = x
- \sqrt{xy} = \sqrt{x} \cdot \sqrt{y}
- \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}}
- \sqrt[n]{x^k} = x^{\frac{k}{n}}
- \sqrt[n]{\sqrt[m]{x}} = \sqrt[n\cdot m]{x}
Príklady:
- \sqrt{24} = \sqrt{4\cdot 6} = \sqrt{4} \cdot \sqrt{6} = 2\sqrt{6}
- \sqrt{3} \cdot \sqrt{3} = (\sqrt{3})^2 = 3
- \sqrt[3]{5^6} = 5^\frac63 = 5^2 = 25
Záporné mocniny
Mocnina so záporným exponentom zodpovedá prevrátenej hodnote príslušnej mocniny s kladným exponentom. Teda x^{-n} = \frac{1}{x^n}. Toto pravidlo je dôsledkom vlastnosti násobenia x^n\cdot x^m = x^{n+m}. Musí teda platiť x^{-n} \cdot x^n = x^{-n+n} = x^0 = 1.
Príklady:
- 2^{-1} = \frac{1}{2} = 0,5
- 2^{-2} = \frac{1}{2^2} = \frac{1}{4} = 0,25
- 10^{-2} = \frac{1}{10^2} = 0,01
- 0,5^{-1} = 2^1 = 2
Vedecký zápis čísel
Vedecký zápis čísel je zápis čísel pomocou súčinu m\cdot 10^n, kde m je reálne číslo (mantisa) a 10^n je mocnina desiatky. Tento zápis čísel je užitočný hlavne pri práci s veľmi veľkými alebo veľmi malými číslami. Napríklad hmotnosť Zeme je približne 5970000000000000000000000 kg, čo je ďaleko prehľadnejšie v zápise 5{,}97\cdot 10^{24} kg. Príklady:
| 5 | 5\cdot 10^0 |
| 0,4 | 4\cdot 10^{-1} |
| 8100 | 8{,}1\cdot 10^{3} |
| 0,032 | 3{,}2\cdot 10^{-2} |
| 8713000000 | 8{,}713\cdot 10^{9} |
| 0,00000000952 | 9{,}52\cdot 10^{-9} |
Logaritmus
Logaritmus je inverzná operácia k umocňovaniu. Logaritmus kladného čísla x pri základe a je také reálne číslo y = \log_a(x), pre ktoré platí a^y = x. Číslo a sa nazýva základ logaritmu (báza).
Logaritmus so základom e=2{,}71828182... (Eulerovo číslo) sa nazýva prirodzený logaritmus a značí sa väčšinou \ln.
Logaritmus so základom 10 sa nazýva dekadický logaritmus (a niekedy sa značí \mathit{lg}).
Logaritmy majú veľmi široké využitie v mnohých oblastiach matematiky. Historicky sa využívali ako užitočná počítacia pomôcka („logaritmické pravítko“), ktorá využívala fakt, že logaritmus súčinu je súčet logaritmov. Dnes na logaritmy často narazíme napríklad v informatike pri návrhu a analýze algoritmov.
Vlastnosti logaritmov:
- Logaritmus je definovaný len pre kladné čísla.
- Logaritmus so základom 1 nie je definovaný.
- Logaritmus jednotky je nula, \log_a(1)=0.
- Logaritmus s rovnakým základom a argumentom je 1, \log_a{a}=1.
- Logaritmus súčinu je súčet logaritmov, \log_a(x\cdot y)=\log_a{x}+\log_a{y}.
- Logaritmus podielu je rozdiel logaritmov, \log_a\left(\frac{x}{y}\right)=\log_a{x}-\log_a{y}.
- Logaritmus je inverzná funkcia k exponenciálnej funkcii s rovnakým základom, \log_a{x}=y \Leftrightarrow a^y=x.
- Logaritmus mocniny je súčin exponentu a logaritmu základu mocniny, \log_a(x^n)=n\log_a{x}.
Graf logaritmu so základom 2:
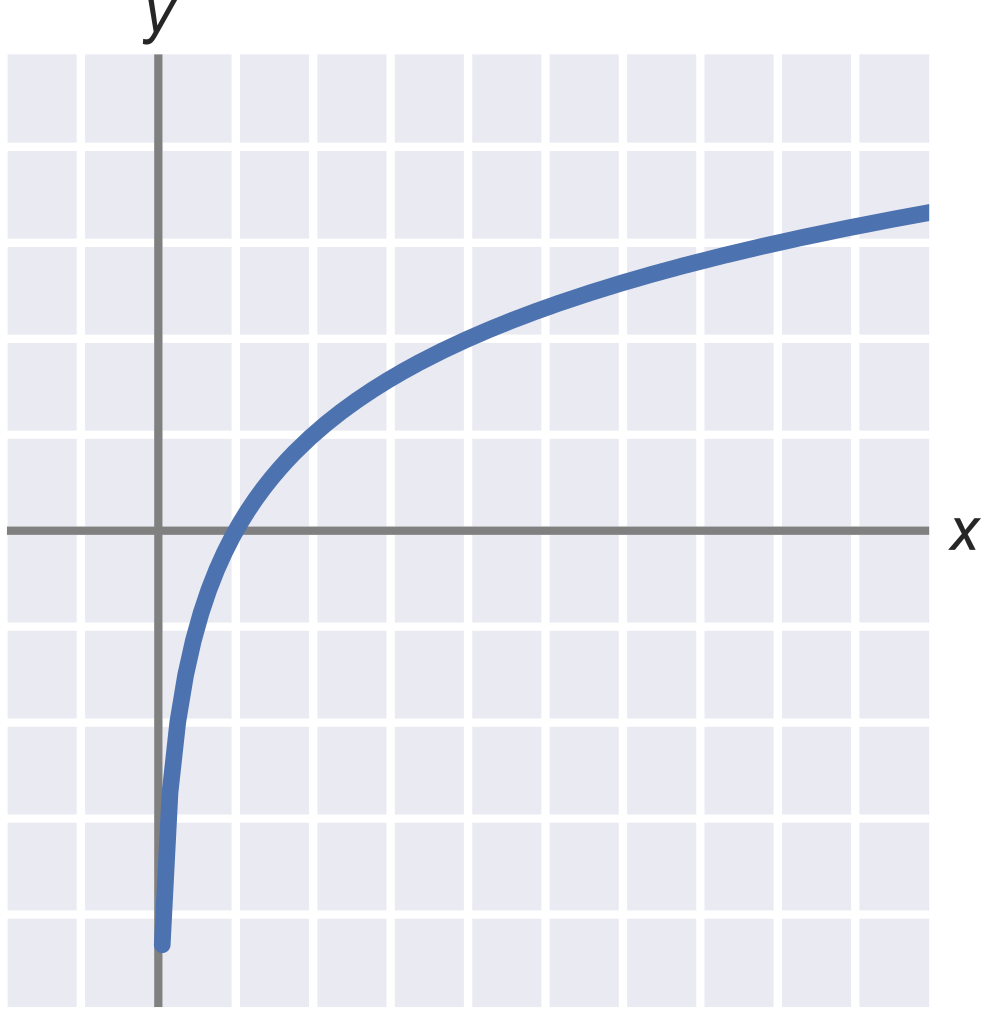
Logaritmus: výpočet
Logaritmus kladného čísla x pri základe a je také reálné číslo y = \log_a(x), pre ktoré platí a^y = x. Príklady:
| \log_{10}(100) = 2 | pretože 10^2 = 100 |
| \log_2(32) = 5 | pretože 2^5 = 32 |
| \log_5(125) = 3 | pretože 5^3 = 125 |
| \log_7(1) = 0 | pretože 7^0 = 1 |
| \log_2(0{,}5) = -1 | pretože 2^{-1} = \frac{1}{2} = 0{,}5 |
Výrazy s logaritmami
Niektoré základné vlastnosti logaritmov vyjadrené pomocou vzorcov:
- \log_a(a)=1
- \log_a(1)=0
- \log_a(x\cdot y) = \log_a(x) + \log_a(y) (logaritmus súčinu je súčet logaritmov)
- \log_a(\frac{x}{y}) = \log_a(x) - \log_a(y) (logaritmus podielu je rozdiel logaritmov)
- \log_a(x^k)=k\log_a(x)
- \log_a(x)=\frac{\log_b(x)}{\log_b(a)}
Číselná os
Číselná os je priamka znázorňujúca čísla. Značkami sú na nej vyznačené vybrané, väčšinou celé, čísla. Popísané sú väčšinou len niektoré značky, inak by sa popisky prekrývali a bolo by to neprehľadné. Zvyšné čísla si dopočítame. Jednoduchý príklad číselnej osi, na ktorej hľadáme číslo 7:

Na základnej číselnej osi majú značky rozostup jedna. To však zďaleka neplatí vždy. Kedykoľvek pracujeme s číselnou osou, musíme si najskôr ujasniť, aký je rozostup medzi značkami. To určíme na základe popiskov. V nasledujúcom príklade je rozostup 10:



 Slovenčina
Slovenčina Angličtina
Angličtina Informatika
Informatika Vieme to
Vieme to Nemčina
Nemčina Biológia
Biológia Zemepis
Zemepis Chémia
Chémia
