Diskrétna matematika
Diskrétna matematika
Diskrétna matematika je zastrešujúca oblasť matematiky, ktorá sa zaoberá štúdiom diskrétnych objektov – jasne oddeliteľných častí. Napríklad Lego kocky alebo karty sú diskrétne. Môžeme ich rôzne kombinovať alebo radiť, ale pracujeme s nimi vždy po jednej, nemá zmysel ich deliť. Naopak taká priamka je spojitá, môžeme ju deliť na stále jemnejšie časti.
Pojem diskrétna matematika aj názvy jednotlivých oblastí môžu znieť abstraktne a zložito. Dajú sa však použiť aj v ľahko predstaviteľných prípadoch ako sú napríklad rôzne hry.
Množiny sú súbory prvkov. Môžeme napríklad zobrať množinu čiernych šachových figúrok alebo množinu futbalových útočníkov. Práca s množinami predstavuje základ mnohých oblastí matematiky.
Logika skúma spôsoby, ako vyvodzujeme závery z predpokladov. Pomocou logiky môžeme dokázať že určitá pozícia v šachu je víťazná pre jedného z hráčov.
Kombinatorika sa zaoberá počítaním možností, ako môžeme objekty vzájomne kombinovať. Pomocou kombinatoriky môžeme určiť počet spôsobov, ako rozdeliť skupinu hráčov do dvoch futbalových tímov.
Pravdepodobnosť skúma pravidlá, ktorými sa riadia náhodné udalosti. Za využitia pravdepodobnosti môžeme vypočítať, ako veľmi (ne)výhodné sú stávky v hazardnej hre s kockami.
Popisná štatistika sa zaoberá popisom javov, ktoré vykazujú vplyv náhody. Pomocou popisnej štatistiky môžeme porovnávať úspešnosť futbalových útočníkov v priebehu sezóny.
Množina je súbor prvkov. Množiny využívame ako čiastkový prvok v mnohých oblastiach matematiky. Príklad z geometrie: kružnica je množina bodov, ktoré majú rovnakú vzdialenosť od stredu. Množiny majú aj mnoho praktických využití. Napríklad pri vývoji internetového obchodu program pracuje s množinou dostupných výrobkov. Množiny sú tiež dôležité na štúdium základov matematiky. Pomáhajú nám napríklad ujasniť si, čo je to nekonečno.
Na prácu s množinami potrebujeme najskôr ovládnuť základné pojmy a značenie a pozrieť sa na rôzne spôsoby, ako môžeme množiny zapísať (výmenovaním, charakteristickou vlastnosťou, štandardným značením).
S množinami môžeme vykonávať množinové operácie ako sú zjednotenie a prienik. Tieto operácie je vhodné si najskôr precvičiť na konkrétnych príkladoch. Keď máme jasno v jednotlivých prípadoch, prichádzajú na rad všeobecné vlastnosti množín a množinových operácií. Na získanie vhľadu a intuície je vhodné zakreslovať si množiny pomocou Vennových diagramov.
Medzi pokročilejšie témy patria množiny množín a potenčná množina.
Množiny: pojmy
Množina je súbor prvkov. Pri množine nie je dôležité poradie prvkov a nezohľadňuje opakované výskyty prvkov. Nasledujúce množiny sú všetky rovnaké:
- \{\square, \bigcirc, \triangle\}
- \{\bigcirc, \triangle, \square\}
- \{\square, \square, \square, \bigcirc, \bigcirc, \triangle\}
| Značenie | Pojem | Komentár |
|---|---|---|
| \emptyset | prázdna množina | |
| \overline{A} | doplnok | prvky, ktoré nepatria do množiny A |
| x \in A | patria do množiny | prvky x patria do množiny A |
| A \cap B | prienik | prvky, ktoré patria do oboch množín A, B |
| A \cup B | zjednotenie | prvky, ktoré patria aspoň do jednej z množín A, B |
| A \setminus B | rozdiel | prvky, ktoré patria do množiny A, ale nepatria do B |
| A = B | rovnosť | rovnosť množín A, B |
| A \subseteq B | podmnožina | všetky prvky množiny A patria aj do množiny B |
| A \subset B | vlastná podmnožina | A je podmnožina B a súčasne A \neq B |
| (zvislá čiara)A(zvislá čiara) | veľkosť množiny | počet prvkov množiny |
| A \cap B = \emptyset | disjunktné množiny | množiny A, B nemajú žiadny spoločný prvok |
Zápis množín
Dôležité číselné množiny majú v matematike svoje štandardné označenie:
| \mathbb{N} | množina prirodzených čísel |
| \mathbb{Z} | množina celých čísel |
| \mathbb{Q} | množina racionálnych čísel |
| \mathbb{R} | množina reálnych čísel |
Ostatné množiny zapisujeme dvomi hlavnými spôsobmi:
Zápis vymenovaním. Jednoducho vymenujeme prvky množiny a zapíšeme ich pomocou zloženej zátvorky. Napríklad M = \{3, 7, 9\} je trojprvková množina obsahujúca čísla 3, 7 a 9.
Symbolický zápis množín. Určíme, zo ktorej množiny prvky vyberáme a akú musia spĺňať vlastnosť. Napríklad M = \{x \in \mathbb{N} \mid x < 10\} je množina prirodzených čísel menších než 10.
Prienik, zjednotenie
| Značenie | Pojem | Komentár |
|---|---|---|
| A \cap B | prienik | prvky, ktoré patria do oboch množín A, B |
| A \cup B | zjednotenie | prvky, ktoré patria aspoň do jednej z množín A, B |
| A \setminus B | rozdiel | prvky, ktoré patria do množiny A, ale nepatria do B |
| A \ominus B | symetrický rozdiel | prvky, ktoré patria práve do jednej z množín A a B |
Znázornenie množinových operácií pomocou Vennových diagramov:
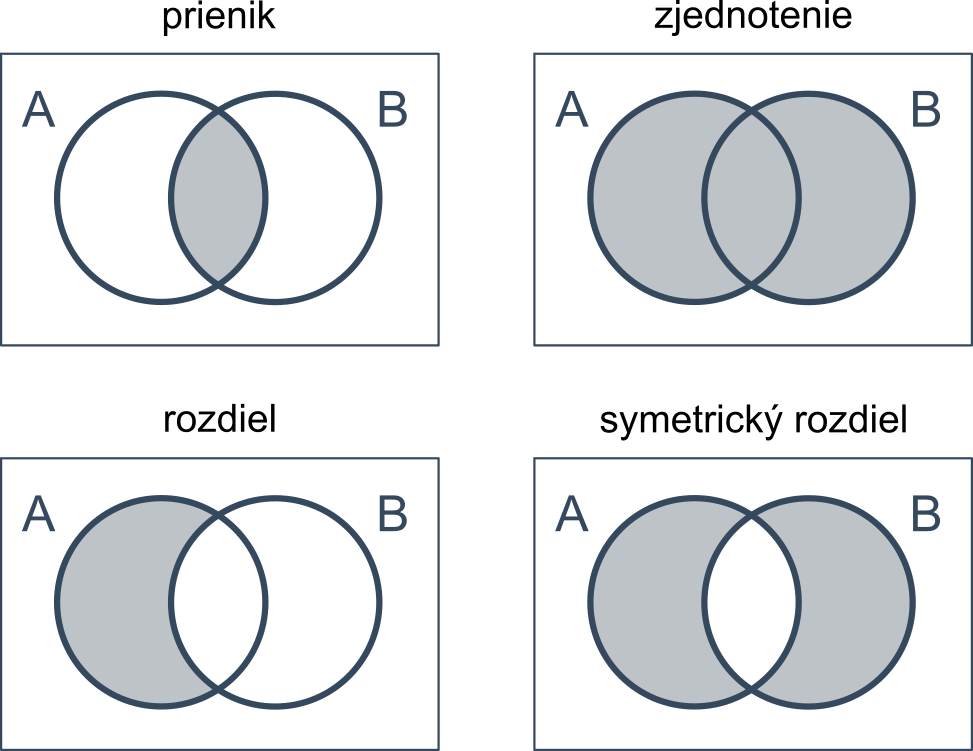
Vlastnosti množín a množinových operácií
- Každá množina je svojou podmnožinou: A\subseteq A.
- Množina nemôže byť svojou vlastnou podmnožinou.
- Prázdna množina je podmnožina akejkoľvek množiny: \emptyset \subseteq A.
- Prázdná množina nemá žiadnu vlastnú podmnožinu.
- A \subseteq A \cup B
- A \cap B \subseteq A
- A \subseteq A \wedge B \subseteq A \Leftrightarrow A=B
Vennove diagramy
Vennov diagram znázorňuje všetky možné vzťahy niekoľkých množín. Vennov diagram znázorňuje prvky množín ako body v rovine a množiny ako plochy vnútri kriviek. Najčastejšie používané sú Vennove diagramy pre dve a tri množiny, v ktorých sú množiny znázornené pomocou kruhov. Je možné stvárniť Vennove diagramy aj v prípade viacerých množín, ale k tomu si už nevystačíme s kruhmi (tieto diagramy nie sú prehľadné, a tak sa príliš nevyužívajú).
Typický Vennov diagram pre tri množiny:
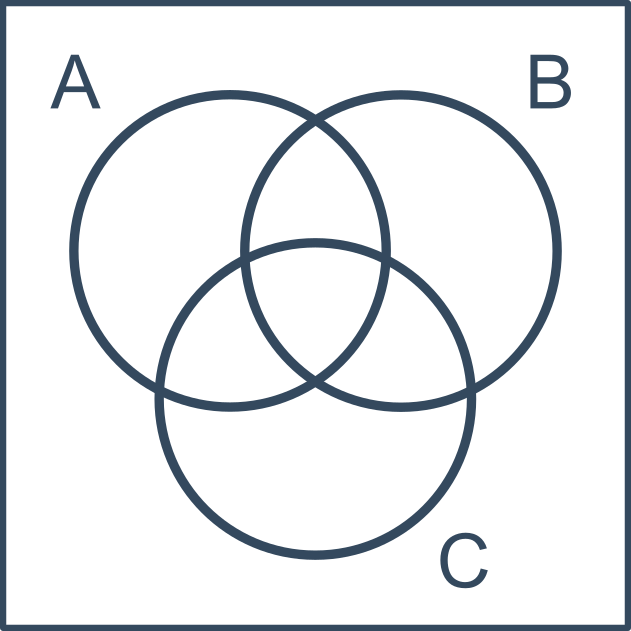
Príklad s konkrétnymi prvkami (množina A obsahuje červené útvary, množina B obsahuje kolieska, množina C obsahuje vyplnené útvary):
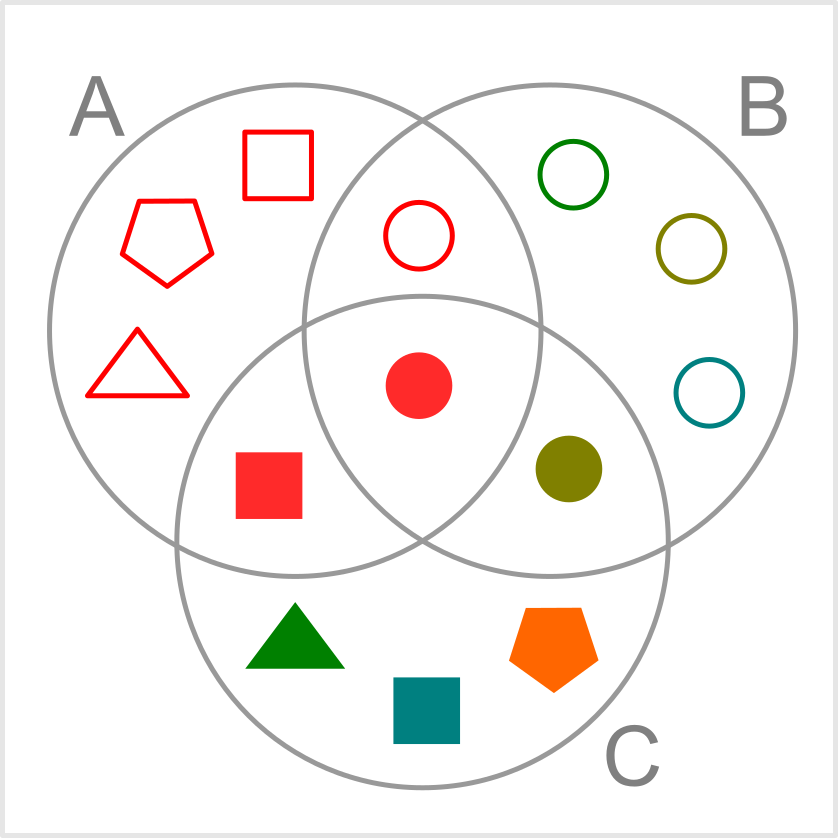
Vennove diagramy využívame napríklad pre názornú ilustráciu množinových operácií. Nasledujúci obrázok ilustruje B \cap (A \cup C):
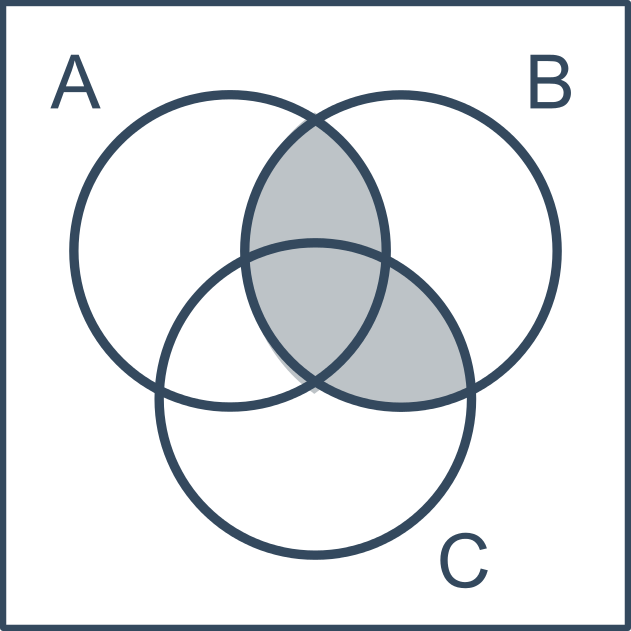
Množiny množín, potenčná množina
Množina prvkom množiny
Prvkom množiny môže byť aj iná množina. S takým prvkom pracujeme rovnako ako s inými prvkami, len sa nesmieme nechať zmiasť.
Príklad: Množina M = \{a, \{b, c, d, e\}, \emptyset\} obsahuje tri prvky:
- „obyčajný“ prvok a
- štvorprvkovú množinu \{b, c, d, e\}
- prázdnu množinu \emptyset
Pozor na rozdiel medzi prázdnou množinou a množinou obsahujúcou prázdnu množinu:
- \emptyset (tiež môžeme písať \{\}) je prázdná množina, jej veľkosť je 0,
- \{\emptyset\} je množina obsahujúca prázdnu množinu, jej veľkosť je 1.
Potenčná množina
Potenčná množina množiny M obsahuje všetky podmnožiny množiny M. Potenčnú množinu značíme \mathcal{P}(M) (existujú aj ďalšie značenia, napríklad 2^M).
Príklad: Pre množinu M = \{a, b, c\} sú všetky jej podmnožiny:
- \{\}
- \{a\}
- \{b\}
- \{c\}
- \{a, b\}
- \{a, c\}
- \{b, c\}
- \{a, b, c\}
Potenčná množina je množina všetkých týchto množín, teda \mathcal{P}(M)=\{\{\}, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}.
Potenčná množina množiny M vždy obsahuje ako svoj prvok samú množinu M. Každá potenčná množina tiež obsahuje ako svoj prvok prázdnu množinu.
Logika skúma spôsoby, ako vyvodzujeme závery z predpokladov. Logika pôvodne vznikla ako súčasť filozofie, neskôr sa výrazne rozvinula v matematike. Dnes má dôležité uplatnenie i v informatike.
Základ matematického poňatia logiky je výroková logika, v ktorej pracujeme s výrokmi (tvrdeniami, ktoré sú buď pravdivé, alebo nepravdivé) a logickými spojkami (a zároveň, alebo, negácia). Rozšírením výrokovej logiky je predikátová logika, v ktorej naviac používame kvantifikátory (existuje, pre každý).
Prehľad tém o logike dostupných na Vieme matiku:
| téma | obsah |
|---|---|
| Logické výroky | slovný zápis logických výrokov |
| Logika: pojmy a značenie | zápis výrokov pomocou logických spojok \wedge, \vee, \neg, \Rightarrow, \Leftrightarrow |
| Vyhodnocovanie logických výrazov | vyhodnocovanie pravdivosti logických výrazov zapísaných pomocou logických operácií |
| Úpravy logických výrazov | úprava a zjednodušenie logického výrazu podľa pravidiel práce s logickými operáciami |
| Kvantifikátory | obohatenie logických výrazov o existenčný a všeobecný kvantifikátor \exists, \forall |
| Dôkazy | exaktné matematické postupy, ako overiť platnosť logických výrokov |
V rámci systémov Vieme nájdete logiku tiež na informatike: logika na Vieme informatiku. Tam je dôraz kladený na logické spojky používané pri programovaní a na riešenie logických úloh.
Logika: pojmy
Výroky
Výrok je zdelenie, pri ktorom má zmysel otázka, či je pravdivý, alebo nepravdivý, pričom môže nastať len jedna z týchto možností.
Príklady výrokov:
- Mesto Košice leží na Slovensku. (pravdivý výrok)
- Košice sú hlavným mestom Slovenskej republiky. (nepravdivý výrok)
- Na Marse je zakopaný poklad. (výrok, ktorého pravdivosť nepoznáme)
Príklady viet, ktoré nie sú výroky: Si hladný? Bež do obchodu pre vajíčka.
Logické spojky
| Zápis | Názov | Význam |
|---|---|---|
| \neg A | negácia | neplatí A |
| A \wedge B | konjunkcia, a zároveň | A a B platia súčasne |
| A \vee B | disjunkcia, alebo | platí aspoň jedno z A a B |
| A \Rightarrow B | implikácia, ak-potom | ak platí A, potom platí aj B |
| A \Leftrightarrow B | ekvivalencia, práve keď | A platí práve vtedy, keď platí B |
Tautológia a kontradikcia
Tautológia je výroková formula, ktorá je vždy pravdivá. Príklady:
- A \vee \neg A (zákon vylúčenia tretieho)
- (A \Rightarrow B) \Leftrightarrow (\neg B \Rightarrow \neg A)
Kontradikcia je výroková formula, ktorá je vždy nepravdivá. Príkladom je formula A \wedge \neg A (zákon sporu).
Formula je splniteľná ak nie je kontradikciou.
Vyhodnocovanie logických výrazov
Pravdivostná tabuľka logických operácií
| A | B | A \vee B | A \wedge B | A \Rightarrow B | A \Leftrightarrow B |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Úpravy logických výrazov
Prepis implikácie a ekvivalencie
| Výrok | Ekvivalentný výrok | |
|---|---|---|
| A\Rightarrow B | \neg A\vee B | |
| A\Rightarrow B | \neg B\Rightarrow \neg A | |
| A\Leftrightarrow B | (A\wedge B)\vee (\neg A \wedge \neg B) |
Negovanie zložených výrokov
| Výrok | Ekvivalentný výrok | |
|---|---|---|
| \neg (\neg A) | A | |
| \neg (A\vee B) | \neg A\wedge \neg B | |
| \neg (A\wedge B) | \neg A\vee \neg B | |
| \neg (A\Rightarrow B) | A\wedge \neg B | |
| \neg (A\Leftrightarrow B) | (\neg A\wedge B)\vee(A \wedge \neg B) |
Pravidlá pre negáciu disjunkcie a konjunkcie (2. a 3. riadok tabuľky) sa nazývajú De Morganove zákony.
Analogické zákony ako pri počítaní s číslami
Pre logické operácie \wedge, \vee tiež platia komutatívne (1. a 2. riadok nasledujúcej tabuľky), asociatívne (3. a 4. riadok) a dištributívne zákony (5. a 6. riadok):
| Výrok | Ekvivalentný výrok | |
|---|---|---|
| A \wedge B | B \wedge A | |
| A \vee B | B \vee A | |
| (A \wedge B) \wedge C | A \wedge (B \wedge C) | |
| (A \vee B) \vee C | A \vee (B \vee C) | |
| A \wedge (B \vee C) | (A \wedge B) \vee (A \wedge C) | |
| A \vee (B \wedge C) | (A \vee B) \wedge (A \vee C) |
Kvantifikátory
Kvantifikátory
| Značenie | Pojem | Význam |
|---|---|---|
| \exists x | existenčný kvantifikátor | existuje x, také že… |
| \forall x | všeobecný (univerzálny) kvantifikátor | pre každé x platí… |
Príklady výrokov s kvantifikátormi
Vlastnosť Číslo x je párne. môžeme vyjadriť ako Existuje celé číslo k také, že x = 2\cdot k. To môžeme zapísať ako \exists k \in \mathbb{Z}: x = 2\cdot k.
Výrok Ponorky (P) nemôžu lietať (L). môžeme zapísať ako \forall x: P(x) \Rightarrow \neg L(x).
V prípade zložitejších výrokov s viacerými kvantifikátormi si musíme dávať pozor na poradie kvantifikátorov:
- \exists x\in M\ \forall y \in M: y \leq x – existuje prvok v množine M, ktorý je väčší alebo rovný všetkým ostatným prvkom v M, teda výrok hovorí, že množina má najväčší prvok.
- \forall x\in M\ \exists y \in M: y \leq x – pre každý prvok v množine M existuje prvok x, ktorý je menší alebo rovný X. Pretože môžeme kľudne vybrať y=x, je to splnené pre každú množinu (pre pokročilých: teda len ak berieme do úvahy množiny čísel a \leq ako bežné usporiadanie na číslach).
Negácia výrokov s kvantifikátormi
Pri negování výrokov s kvantifikátormi meníme existenčný kvantifikátor na všeobecný (a naopak) a posúvame negáciu „dovnútra“. Príklad:
- Nie je pravda, že všetky mačky (M) sú čierne ( C ).
- \neg (\forall x: M(x) \Rightarrow C(x))
- Zmeníme všeobecný kvantifikátor na existenčný a znegujeme výrok.
- \exists x: \neg(M(x) \Rightarrow C(x))
- Teraz znegujeme implikáciu pomocou pravidla \neg(A \Rightarrow B) \Leftrightarrow (A \wedge \neg B).
- \exists x: M(x) \wedge \neg C(x)
- Existuje mačka, ktorá nie je čierna.
Permutácie, kombinácie, variácie
- Permutácia je usporiadanie prvkov do fixného poradia.
- Kombinácia (k prvková) je výber k prvkov zo zadanej množiny.
- Kombinácia s opakovaním (k prvková) je výber k prvkov zo zadanej množiny, pričom prvky sa môžu opakovať.
- Variácia (k prvková) je usporiadaný výber k prvkov zo zadanej množiny.
- Variácia s opakovaním (k prvková) je usporiadaný výber k prvkov zo zadanej množiny, pričom prvky sa môžu opakovať.
Príklady:
| permutácia | \{A, B, C\} | ABC, ACB, BAC, BCA, CAB, CBA |
| kombinácia | \{A, B, C, D\}; k=2 | AB, AC, AD, BC, BD, CD |
| kombinácia s opakovaním | \{A, B, C, D\}; k=2 | AA, AB, AC, AD, BB, BC, BD, CC, CD, DD |
| variácia | \{A, B, C, D\}; k=2 | AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB, DC |
| variácia s opakovaním | \{A, B, C\}; k=2 | AA, AB, AC, BA, BB, BC, CA, CB, CC |
Počty permutácií, kombinácií a variácií udáva nasledovná tabuľka:
| počet všetkých permutácií n prvkov | n! |
| počet všetkých k prvkových kombinácií z n prvkov | \binom{n}{k} = \frac{n!}{(n-k)!k!} |
| počet všetkých k prvkových kombinácií s opakovaním z n prvkov | \binom{n + k - 1}{k} |
| počet všetkých k prvkových variácií z n prvkov | \frac{n!}{(n-k)!} |
| počet všetkých k prvkových variácií s opakovaním z n prvkov | n^k |
Kombinačné čísla
Kombinačné číslo udáva počet kombinícií, teda spôsobov, ako vybrať k prvkov z n prvkovej množiny. Kombinačné čísla sa vyskytujú veľmi často v kombinatorických výpočtoch, a preto majú špeciálne značenie \binom{n}{k} (čítame „n nad k“).
Pre n \geq k \geq 0 platí: \binom{n}{k} = \frac{n!}{k!(n-k)!}
Pre kombinačné čísla platí rad ďalších vzťahov, napríklad:
- \binom{n}{k} = \binom{n}{n-k}
- \binom{n+1}{k} = \binom{n}{k} + \binom{n}{k-1}
- \sum_{k=0}^n \binom{n}{k} = 2^n
Príklady:
| \binom{3}{1} | = 2 |
| \binom{4}{2} | = 6 |
| \binom{5}{3} | = 10 |
| \binom{6}{2} | = 15 |
| \binom{15}{15} | = 1 |
Pravdepodobnosť: pojmy a značenie
Náhodný jav je výsledok náhodného pokusu, o ktorom je možné po vykonaní pokusu rozhodnúť, či nastal alebo nenastal. Jeho typickým rysom je, že môže, ale nemusí nastať. Pravdepodobnosť javu je miera očakávania, že jav nastane. Pravdepodobnosť je číslo medzi 0 a 1. V bežnom jazyku vyjadrujeme často pravdepodobnosť v percentách, čo je stonásobok pravdepodobnosti používanej v matematike.
Pojmy a značenie
| jav elementárny | 0 \leq P(A) \leq 1 | základný výsledok pokusu, ktorý nie je možné ďalej rozložiť |
| jav istý | P(A) = 1 | nastane vždy |
| jav nemožný | P(A) = 0 | nenastane nikdy |
| B je jav opačný k javu A | P(B) = 1-P(A) | B nastane práve vtedy, keď nenastane A |
| javy A a B sú nezlúčiteľné | A\cap B=\emptyset | javy A a B nemôžu nastať súčasne |
Príklad
- Vo vrecku mám päť guľôčok, z toho dve sú červené, dve modré a jedna žltá. Guľôčky sa okrem farby nelíšia. Pokus spočíva v tom, že z vrecka námatkovo vytiahnem guľôčku.
- „Vytiahnem červenú guľôčku.“ je náhodný jav. Ide o jav elementárny. Jeho pravdepodobnosť je 0,4 (v bežnej reči by sme mohli povedať 40 %).
- „Vytiahnem červenú alebo žltú guľôčku.“ je zložený jav. Jeho pravdepodobnosť je 0,6.
- „Vytiahnem guľôčku.“ je jav istý.
- „Vytiahnem zelenú guľôčku.“ je jav nemožný.
Priemer a medián
Priemer a medián sú miery centrálnej (strednej) tendencie, vyjadrujú teda „typickú“ hodnotu premenných z určitej vzorky.
Priemer je súčet hodnôt vydelený ich počtom. Presnejšie povedané ide o aritmetický priemer (existujú aj iné druhy priemerov, napr. harmonický či geometrický).
Medián je stredná hodnota zo zoradenej postupnosti hodnôt. Je definovaný ako hodnota väčšia alebo rovná polovici hodnôt v súbore a menšia alebo rovná polovici hodnôt v súbore.
Príklad: Zoberme si súbor hodnôt 10, 3, 8, 4, 5. Priemer je súčet delený počtom, teda 30:5=6. Na určenie mediánu hodnoty najskôr zoradíme: 3, 4, 5, 8, 10. Medián je stredná hodnota, teda 5.
Ak má súbor párny počet prvkov, väčšinou sa za medián označuje priemer dvoch stredných hodnôt. Napríklad pre súbor hodnôt 10, 2, 9, 4, 14, 5 je zoradená postupnosť 2, 4, 5, 9, 10, 14. Hodnoty uprostred postupnosti sú 5 a 9, medián je teda 7.
Niekedy máme súbor hodnôt, ktoré je možné usporiadať podľa veľkosti, ale nie je možné vypočítať aritmetický priemer dvoch hodnôt. Napríklad pre súbor štyroch hodnôt S, M, XL, XXL veľkostí oblečenia spĺňa definíciu mediánu akákoľvek hodnota od M do XL, teda M, L, i XL.
Kvantily a kvartily
Kvantily sú charakteristiky polohy štatistického znaku podobne ako napr. aritmetický priemer a medián. Kvantily je možné určiť pre ordinálne, intervalové a pomerné typy dát.
Súbor n hodnôt usporiadame podľa veľkosti: x_1 \le x_2 \le \ldots \le x_{n-1} \le x_n
Majme číslo \theta medzi nulou a jednotkou. Kvantil Q_{\theta} je hodnota, ktorá delí usporiadanú postupnosť hodnôt v súbore na dolnú a hornú časť tak, že dolná časť obsahuje aspoň \theta \cdot n hodnôt a horná časť aspoň (1-\theta)\cdot n hodnôt.
x_1 \le \ldots \le x_c \le Q_{\theta} \le x_{c+1} \le \ldots \le x_n
- Ak je \theta \cdot n necelé číslo, a najbližšie väčšie celé číslo je k, väčšinou zvolíme Q_{\theta}=x_k.
- Ak je \theta \cdot n=m celé číslo, zvolíme Q_{\theta} = \frac{x_{m}+x_{m+1}}{2} (keď je možné tento aritmetický priemer spočítat — teda pre intervalové a pomerové znaky).
Napríklad vezmeme súbor ôsmich čísel 0,0,0,0,1,2,3,4. Kvantil Q_{0{,}1} určíme takto: 0{,}1 \cdot 8 = 0{,}8, najbližšie väčšie celé číslo je 1, takže Q_{0{,}1}=x_1=0. Kvantil Q_{0{,}75} určíme takto: 0{,}75 \cdot 8 = 6, takže Q_{0{,}75}=\frac{x_6+x_7}{2}=\frac{2+3}{2}=2{,}5.
Pre ordinálne znaky nemusí byť možné vypočítať aritmetický priemer. Ako kvantil Q_{\theta} potom zvolíme niektorú hodnotu, ktorá vhodne delí usporiadanú postupnosť hodnôt súboru.
Napríklad spočítajme kvantil Q_{0{,}8} pre hodnoty S, S, M, L, XXL znaku „veľkosť oblečenia“. 5 \cdot 0{,}8=4, Q_{0{,}8} je akákoľvek hodnota medzi x_4 a x_5, teda L,XL, alebo XXL.
p% kvantil Q_{\frac{p}{100}} sa nazýva p. percentil.
Niektoré významné kvantily:
| kvantil | názov |
|---|---|
| Q_{0{,}5} | medián |
| Q_{0{,}25} | dolný kvartil |
| Q_{0{,}75} | horný kvartil |
| Q_{0{,}01},Q_{0{,}02},\ldots, Q_{0{,}99} | 1. percentil, 2. percentil, … , 99.percentil |
Medzikvartilové rozpätie je rozdiel horného a dolného kvartilu: Q_{0{,}75}-Q_{0{,}25} Medzikvartilové rozpätie (niekedy označované ako IQR) je možné vypočítať pro intervalové a pomerové znaky.
Napríklad, určime medzikvartilové rozpätie pre súbor hodnôt 0,0,0,0,1,2,3,4. Horný kvartil Q_{0{,}75} sme vypočítali už skôr, je to 2{,}5. Dolný kvartil Q_{0{,}25} je \frac{x_2+x_3}{2}=\frac{0+0}{2}=0. Medzikvartilové rozpätie je 2{,}5-0=2{,}5.
Absolútna a relatívna početnosť
Štatistický súbor má rozsah n, keď obsahuje presne n jednotiek. Napríklad štatistickým súborom s rozsahom 10 môže byť skupinka 10 detí z tretej triedy. Jednotliví žiaci a žiačky sú potom jednotkami štatistického súboru.
Príklady štatistických znakov, ktoré nás môžu zaujímať: meno, výška, známka z prvouky. Predpokladajme, že mená detí z našej skupinky desiatich žiakov a žiačok sú: Anna, Eva, Ján, Ján, Ján, Vanesa, Vanesa, Mirka, Tobiáš, Tomáš.
Znak meno teda v našom štatistickom súbore nadobúda siedmich rôznych hodnôt – Anna, Eva, Ján, Vanesa, Mirka, Tobiáš, Tomáš. Niektoré deti môžu mať rovnaké meno.
Absolútnou početnosťou hodnoty znaku v danom štatistickom súbore je počet jednotiek zo štatistického súboru, ktoré majú danú hodnotu znaku.
Napríklad absolútna početnosť hodnoty „Ján“ znaku meno je 3, pretože v skupinke sú traja žiaci s menom Ján. Absolútna početnosť hodnoty „Eva“ znaku meno je 1.
Relatívnu početnosť hodnoty znaku v danom štatistickom súbore vypočítame ako podiel počtu jednotiek s danou hodnotou znaku počtom všetkých jednotiek štatistického súboru. Tiež sa dá povedať, že relatívna početnosť hodnoty znaku je podiel absolútnej početnosti tejto hodnoty znaku a rozsahu n štatistického súboru. Relatívna početnosť sa zadáva ako číslo v intervale [0,1] alebo v percentách.
Napríklad relatívna početnosť hodnoty „Vanesa“ znaku meno je \frac{2}{10}=0{,}2, pretože v skupinke celkovo desiatich detí sú dve žiačky s menom Vanesa. Relatívnu početnosť hodnoty „Vanesa“ znaku meno môžeme zapísať tiež ako 20\ \%.
Súčet absolútnych početností všetkých hodnôt jedného znaku sa rovná rozsahu n daného štatistického súboru.
Súčet relatívních početností všetkých hodnôt jedného znaku je 1 alebo tiež 100\ \%.
Korelačný koeficient
Korelácia je vzťah medzi dvomi veličinami. Korelačný koeficient je číslo, ktoré vyjadruje silu tohto vzťahu.
Existuje viac spôsobov, ako koreláciu merať. Najčastejšie používaný je Pearsonov korelačný koeficient. Ten sa značí r a má nasledujúce vlastnosti:
- Nadobúda hodnôt z intervalu [-1, 1].
- Meria len lineárnu závislosť medzi veličinami.
- Ak je hodnota kladná, zodpovedá zväčšenie jednej veličiny zväčšeniu druhej.
- Ak je hodnota záporná, zodpovedá zväčšenie jednej veličiny zmenšeniu druhej.
- Ak je hodnota nulová, nie je medzi veličinami lineárna závislosť.
- Ak je hodnota presne 1 alebo -1, je medzi veličinami presná lineárna závislosť.
Typy štatistických dát
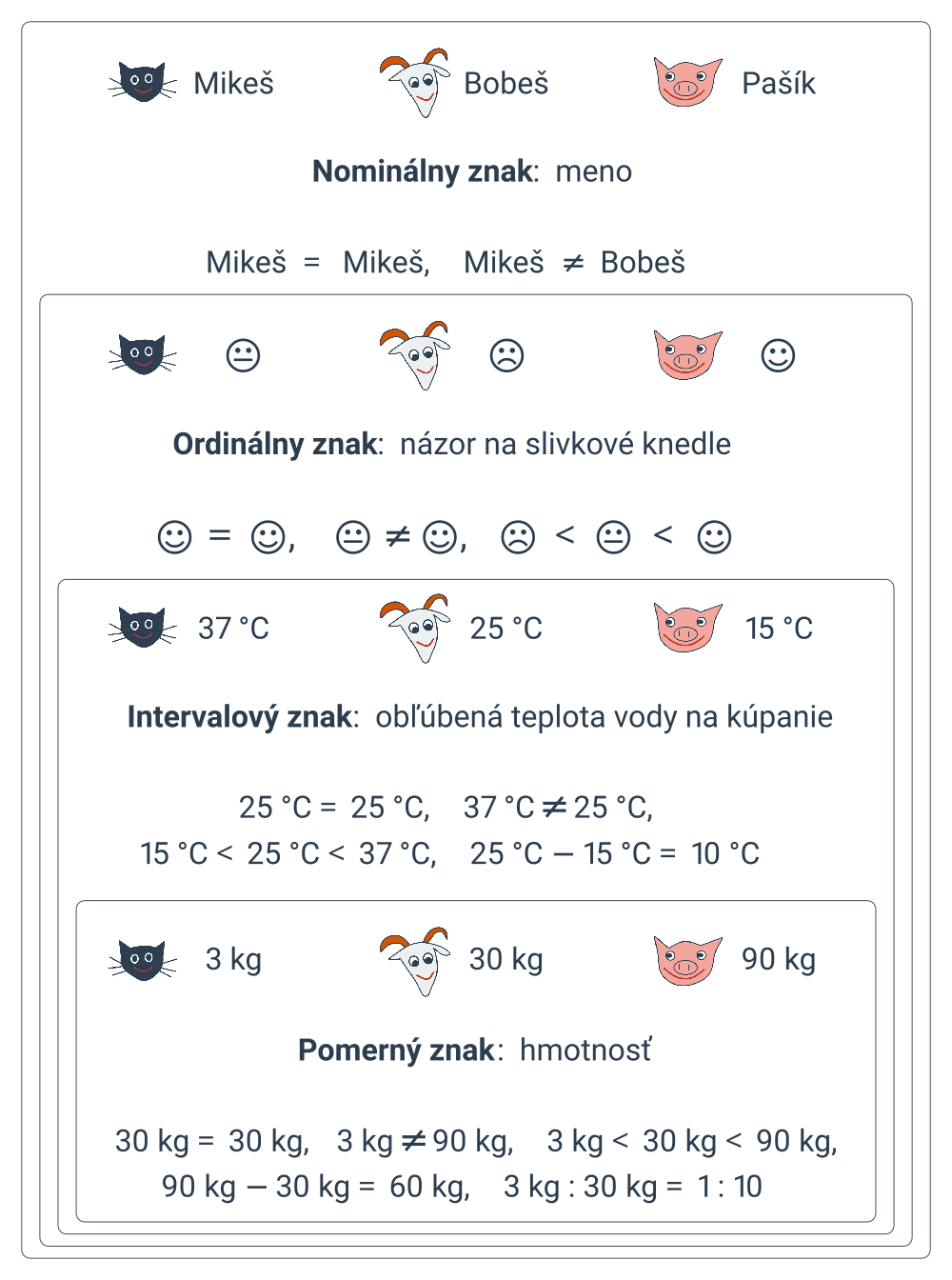
Zamyslime sa nad štatistickým súborom zvieratiek z Hrusíc. Vezmime z neho tri jednotky na ukážku: kocúrika Mikeša, kozla Bobeša a prasiatko Pašíka. Budeme si pri nich všímať rôzne typy znakov.
Nominálny znak nadobúda hodnôt, pri ktorých môžeme testovať rovnosť, teda určiť, či sú rovnaké alebo rôzné. Napríklad meno, farba.
Ordinálny znak nadobúda hodnôt, pri ktorých môžeme testovať rovnosť a ktoré ešte aj dokážeme porovnávať, teda určiť, ktorá z dvoch rôznych hodnôt je menšia a ktorá väčšia. Napríklad známka z matematiky, veľkosť oblečenia (XS, S, M, L, XL), obľuba brokolicovej polievky („fuj“,„dá sa“,„mňam“).
Intervalový znak nadobúda hodnôt, pri ktorých môžeme testovať rovnosť, porovnávať ich a určiť rozdiel dvoch hodnôt, teda rovnaký interval medzi jednou a druhou dvojicou hodnôt vyjadruje aj rovnaký rozdiel v intenzite skúmanej vlastnosti. Napríklad teplota v stupňoch Celzia, rok narodenia.
Pomerný znak nadobúda hodnôt, pri ktorých môžeme testovať rovnosť, porovnávať ich, určiť rozdiel dvoch hodnôt a určiť pomer dvoch hodnôt, teda spočítať ich podiel, ktorý zmysluplne vyjadruje koľkokrát je jedna hodnota väčšia než druhá. Napríklad teplota v stupňoch Kelvina, hmotnosť. Teplota v stupňoch Celzia môže ísť aj do záporných čísel a teleso s teplotou 10 °C nemá dvakrát väčšiu kinetickú energiu častíc než teleso s teplotou 5 °C, takže teplota v stupňoch Celzia nie je pomerný znak.
Alternatívny znak je pojem mimo túto hierarchiu, znamená to, že znak nadobúda len dve hodnoty. Napríklad zdravý – chorý, s topánkami – bez topánok.
Priemer, medián a modus (použitie)
Aritmetický priemer, medián a modus sú charakteristiky polohy znaku. Používame ich k popisu typickej hodnoty znaku.
Aritmetický priemer pre daný súbor sa počíta ako podiel súčtu hodnôt znaku rozsahom súboru.
- Aritmetický priemer je možné vypočítať pre intervalové a pomerové znaky.
- Najlepšie sa hodí k popisu typickej hodnoty znaku, ktorý nadobúda v danom súbore podobných hodnôt bez príliš odlišných extrémov, ktoré by aritmetický priemer vychýlili mimo typické hodnoty.
Príklad použitia aritmetického priemeru – súbor hodnôt 122, 116, 120, 118 znaku „výška dieťaťa v cm“ má aritmetický priemer 119.
Medián delí rad vzostupne zoradených hodnôt na dve rovnako početné polovice.
- Pre nepárny počet hodnôt je medián stredný prvok.
- Pre párny počet hodnôt môže definícii mediánu zodpovedať viac hodnôt, niekedy sa v takom prípade berie ako medián aritmetický priemer dvoch prostredných hodnôt (samozrejme len ak pre daný znak aritmetický priemer môžeme vypočítať).
- Medián je možné určiť pre ordinálne, intervalové a pomerové znaky.
- Nie je ovplyvnený extrémnymi hodnotami ako aritmetický priemer.
Príklad použitia mediánu – súbor hodnôt 1, 1000, 1002, 1003 znaku „hmotnosť krokodíla v kg“ má medián 1001 (alebo akékoľvek číslo od 1000 do 1002). Extrémne malá hodnota 1 spôsobí, že aritmetický priemer je 751{,}5, čo nezodpovedá typickej hodnote „niečo málo cez 1000 kg“.
Modus je hodnota znaku, ktorá má v danom súbore najväčšiu relatívnu (i absolútnu) početnosť.
- Takých hodnôt môže byť viac než jedna.
- Modus môžeme vypočítať pre nominálne, ordinálne, intervalové a pomerové znaky.
Príklad použitia – modus súboru hodnôt 1, 1, 1, 1, 2, 2 znaku „počet hrbov ťavy“ je 1.


 Slovenčina
Slovenčina Angličtina
Angličtina Informatika
Informatika Vieme to
Vieme to Nemčina
Nemčina Biológia
Biológia Zemepis
Zemepis Chémia
Chémia
