Funkcie
Základné typy funkcií
Grafy základných typov funkcií:
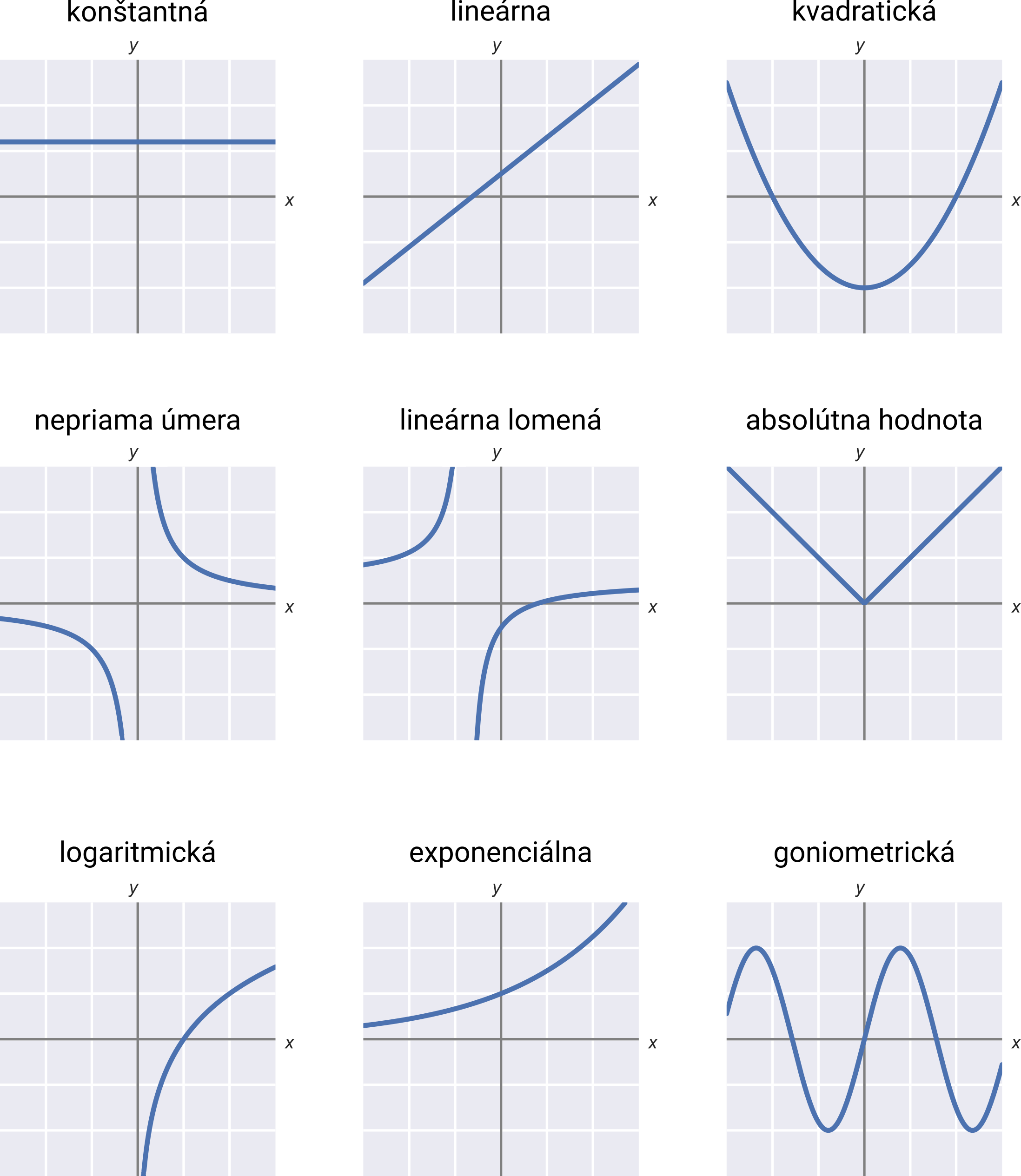
Vlastnosti funkcií
Pozn. V rámci zjednodušenia popisu berieme do úvahy len funkcie, ktorých definičný obor tvoria všetky reálne čísla.
Funkcia f sa nazýva párna práve vtedy, keď je pre každé x f(-x) = f(x). Graf párnej funkcie je súmerný podľa osi y. Príklady párnych funkcií: f_1(x) = x^2, f_2(x) = \cos(x), f_3(x) = x^4-3x^2+2.
Funkcia f sa nazýva nepárna práve vtedy, keď je pre každé x f(-x) = -f(x). Graf nepárnej funkcie je súmerný počiatku. Príklady nepárnych funkcií: f_1(x) = 3x, f_2(x) = \sin(x), f_3(x) = x^3-2x.
Funkcia f sa nazýva periodická práve vtedy, keď existuje číslo p != 0 (perióda funkcie) také, že pre každé x platí f(x+p)=f(x). Typickými príkladmi periodických funkcií sú funkcie goniometrické. Naopak napríklad polynómy periodické nie sú (s výnimkou konštantnej funkcie).
Funkcia f sa nazýva zdola obmedzená práve vtedy, keď existuje také číslo k, že pre každé x platí f(x) \geq k. Funkcia f sa nazýva zhora obmedzená, práve keď existuje také číslo k, že pre každé x platí f(x) \leq k. Funkcia f sa nazýva obmedzená, keď je súčasne obmedzená zhora aj zdola. Príklady:
- Funkcia f(x) = \sin(x) je obmedzená.
- Funkcia f(x) = x^2 je obmedzená zdola (pretože \forall x: f(x) \geq 0), ale nie je obmedzená zhora.
- Funkcia f(x) = 2x nie je obmedzená ani zhora, ani zdola.
Funkcia f sa nazýva prostá práve vtedy, keď pre každú dvojicu x_1 \neq x_2 platí f(x_1) \neq f(x_2).
Funkcia f sa nazýva rastúca práve vtedy, keď pre každú dvojicu x_1 < x_2 platí f(x_1) < f(x_2).
Funkcia f se nazýva klesajúca práve vtedy, keď pre každú dvojicu x_1 > x_2 platí f(x_1) > f(x_2).
Graf lineárnej funkcie
Lineárnu funkciu môžeme vždy zapísať v tvare f(x) = a\cdot x + b, kde a a b sú konštanty. Parameter a je smernica (tiež nazývaná sklon), parameter b je absolútny člen. Grafom lineárnej funkcie je priamka, pričom platí:
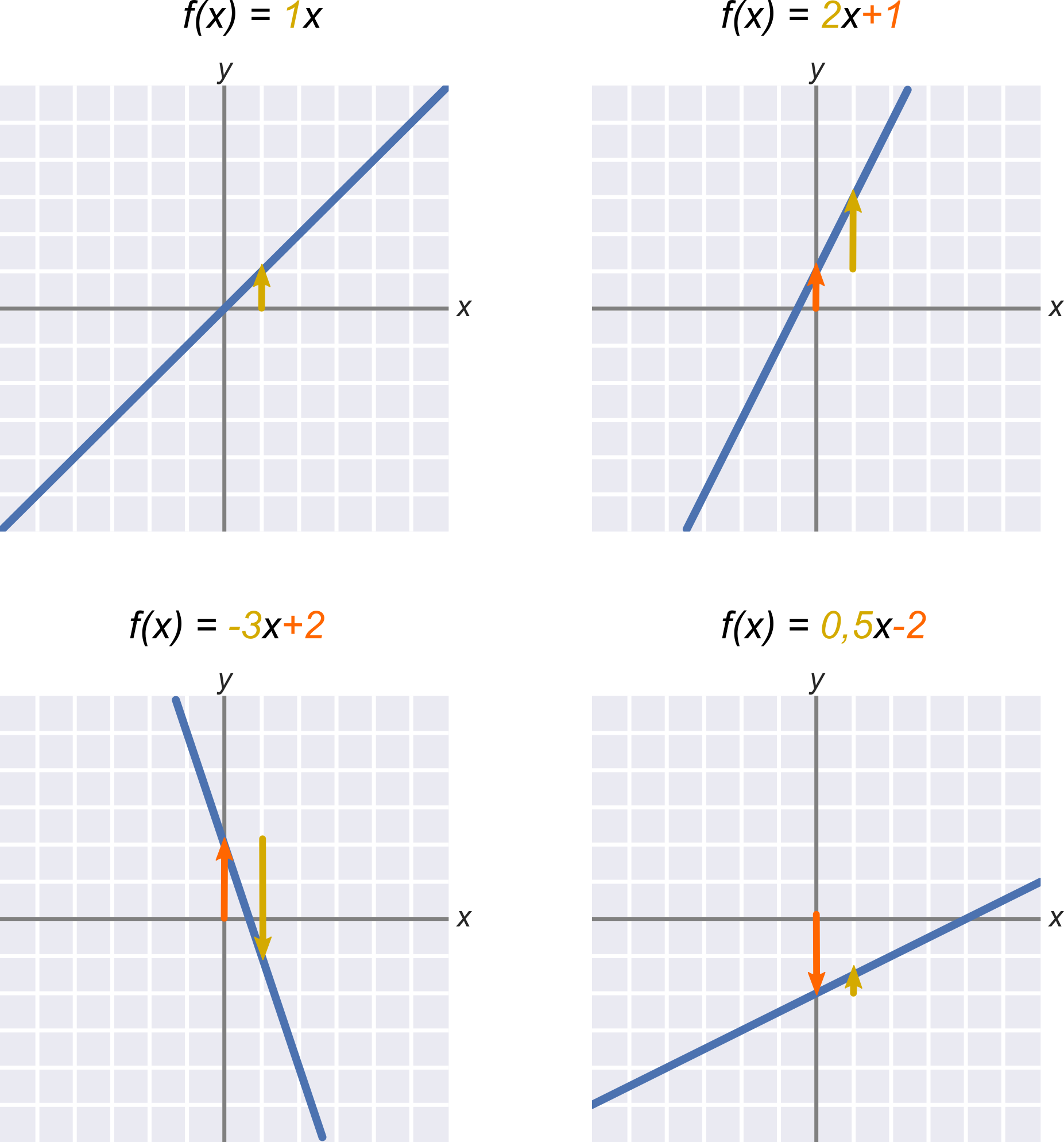
- Absolútny člen b udáva „zvislý posun“. Je to priesečník priamky s osou y. V uvedených príkladoch je vyznačený oranžovou farbou.
- Smernica a udáva sklon priamky, čo môžeme vyjadriť ako „o koľko jednotiek na osi y sa priamka posunie za jednu jednotku na osi x“. V uvedených príkladoch je smernica vyznačená žltou farbou.
Dôležité sú znamienka (naznačené v obrázkoch šípkami). Kladný absolútny člen znamená posun hore, záporný absolútny člen znamená posun dole. Kladná smernica znamená stúpajúcu priamku, záporná smernica znamená klesajúcu priamku.
Grafy kvadratických funkcií
Kvadratickú funkciu je možné vyjadriť v tvare f(x) = ax^2 + bx + c, kde a\neq 0. Grafom kvadratickej funkcie je parabola. Tento graf zobrazuje funkciu 0{,}5 x^2 + x - 4:
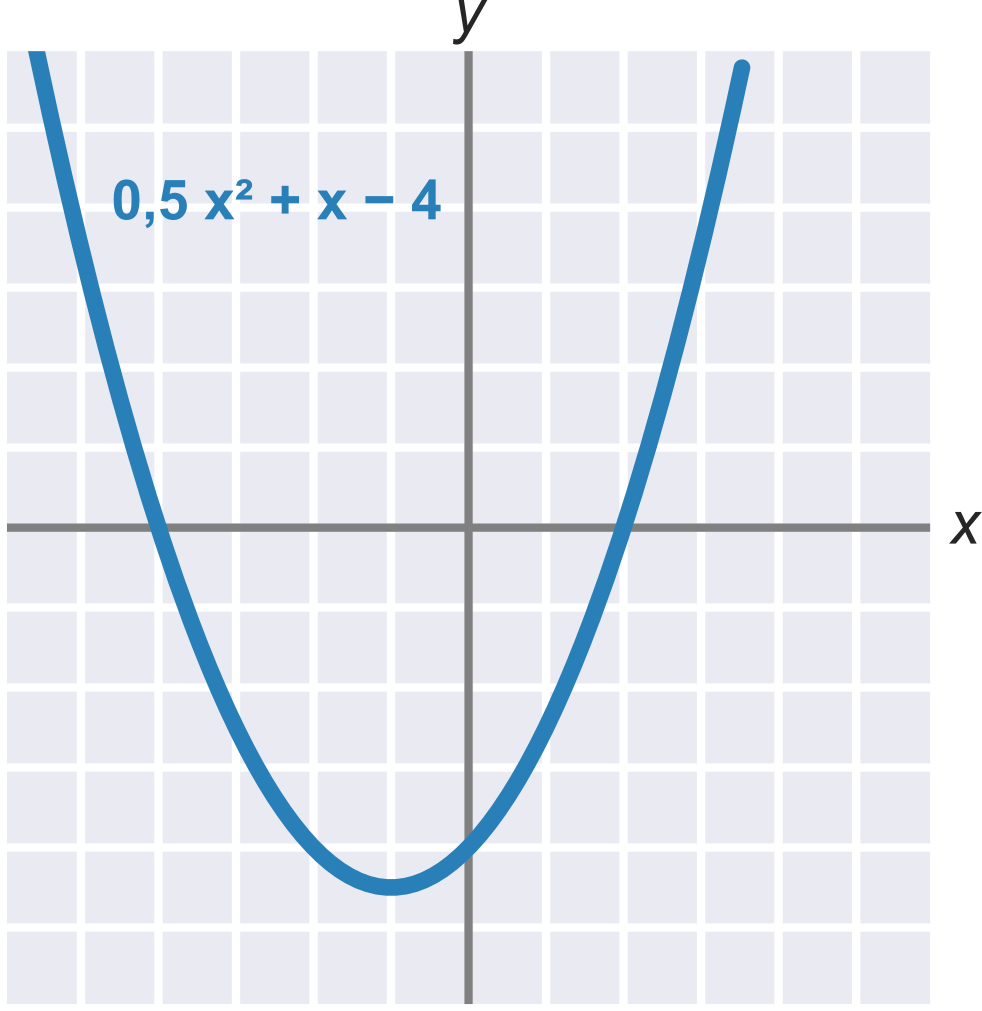
Priesečníky s osou x sú riešenia kvadratickej rovnice ax^2 + bx + c = 0. Pre vyššie uvedený príklad 0{,}5 x^2 + x - 4 sú týmito riešeniami x_1 = -4 a x_2 = 2.
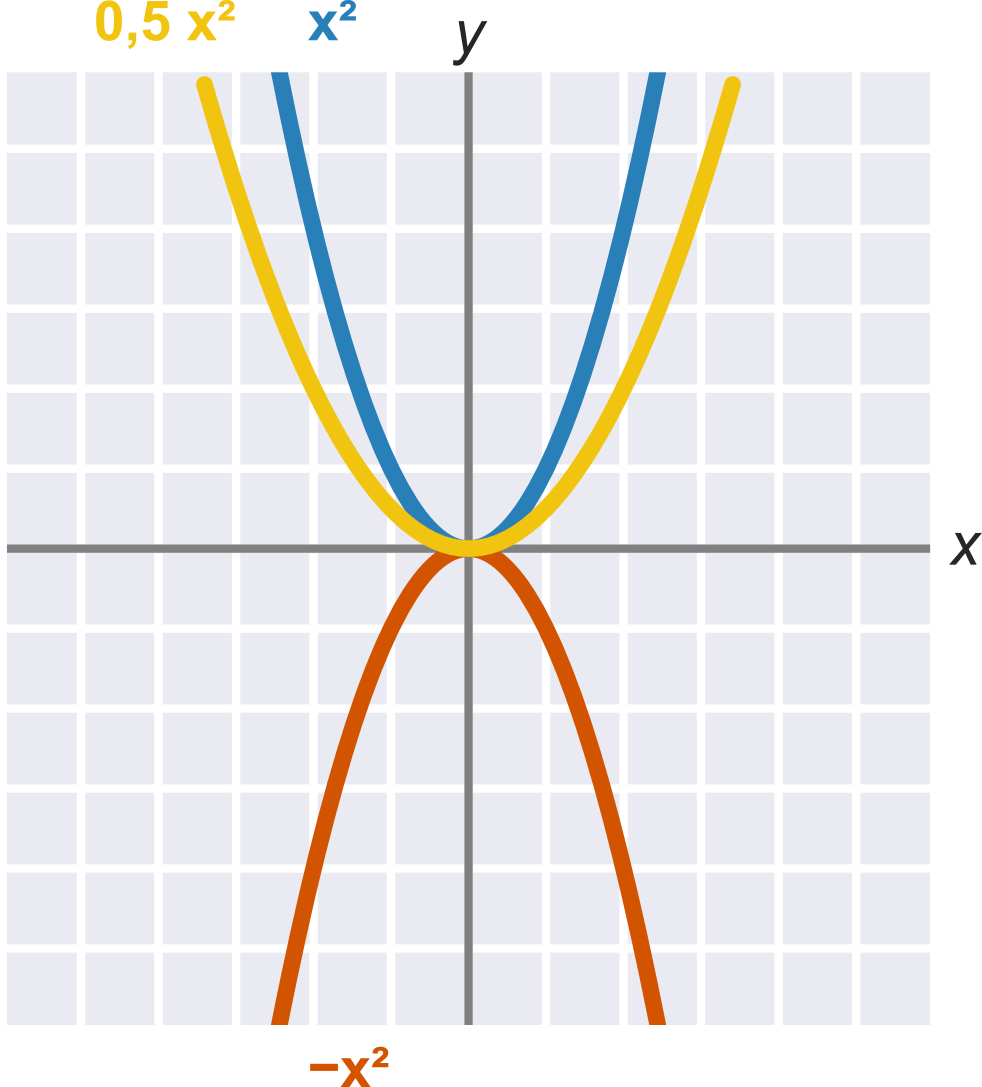
Kvadratický koeficient a ovplyvňuje základnú podobu paraboly:
- Ak je a>0, „smeruje parabola hore“ (presnejšie: je to zdola obmedzená, konvexná funkcia).
- Ak je a<0, „smeruje parabola dole“ (presnejšie: je to zhora obmezená, konkávna funkcia).
- Veľkost kvadratického koeficientu a ovplyvňuje, ako je parabola „široká“.
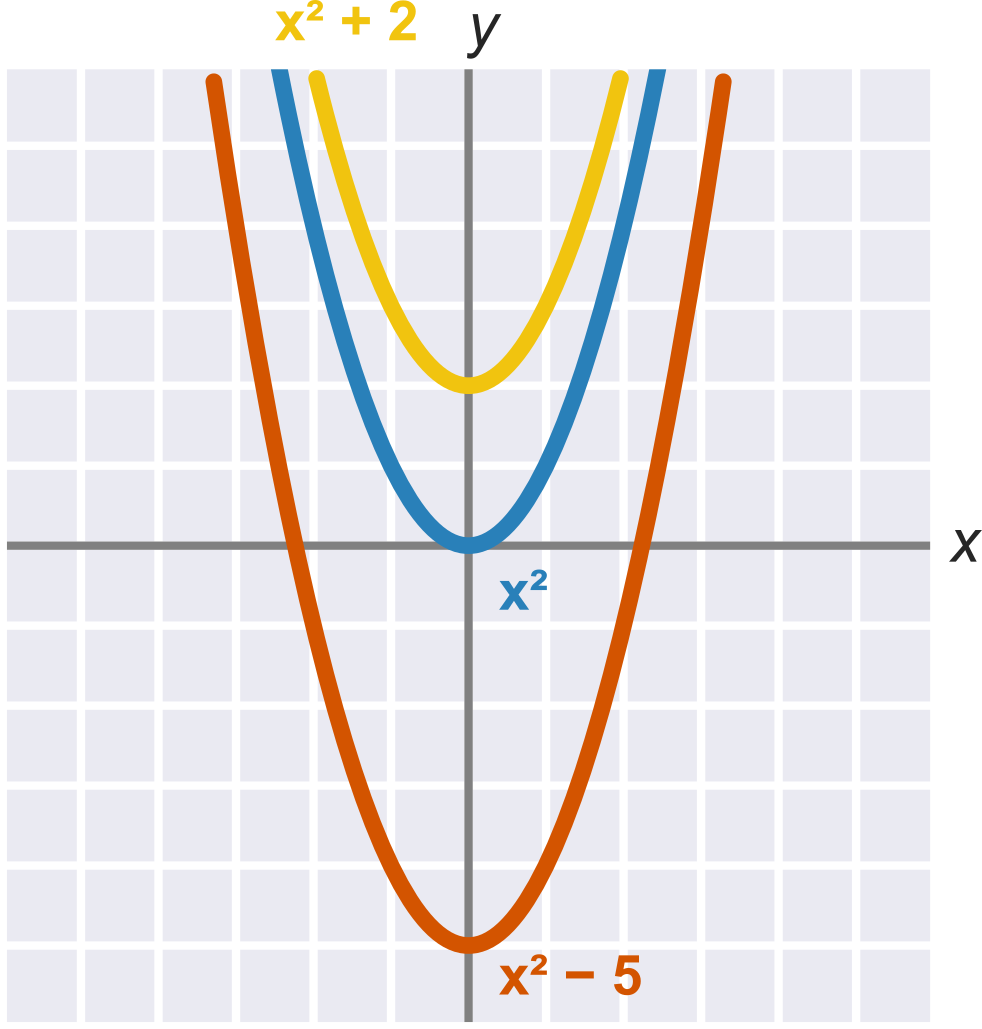
Konštantný člen c ovplyvňuje posun paraboly – udáva priesečník s osou y.
Syntax highlighting test, please ignore:
Grafy goniometrických funkcií
Grafy základných goniometrických funkcií

Dopad úprav funkcie na graf

Obrázok ukazuje grafy niekoľkých úprav funkcie \sin(x).
| \sin(x+1) | graf má posunutú fázu (posun v smere osi x) |
| \sin(x)+1 | graf je posunutý v smere osi y |
| \sin(2x) | funkcia má zmenenú dĺžku periódy |
| 2\sin(x) | funkcia má zmenenú veľkost amplitúdy |
Grafy exponenciálnych a logaritmických funkcií
Grafy exponenciálnych funkcií
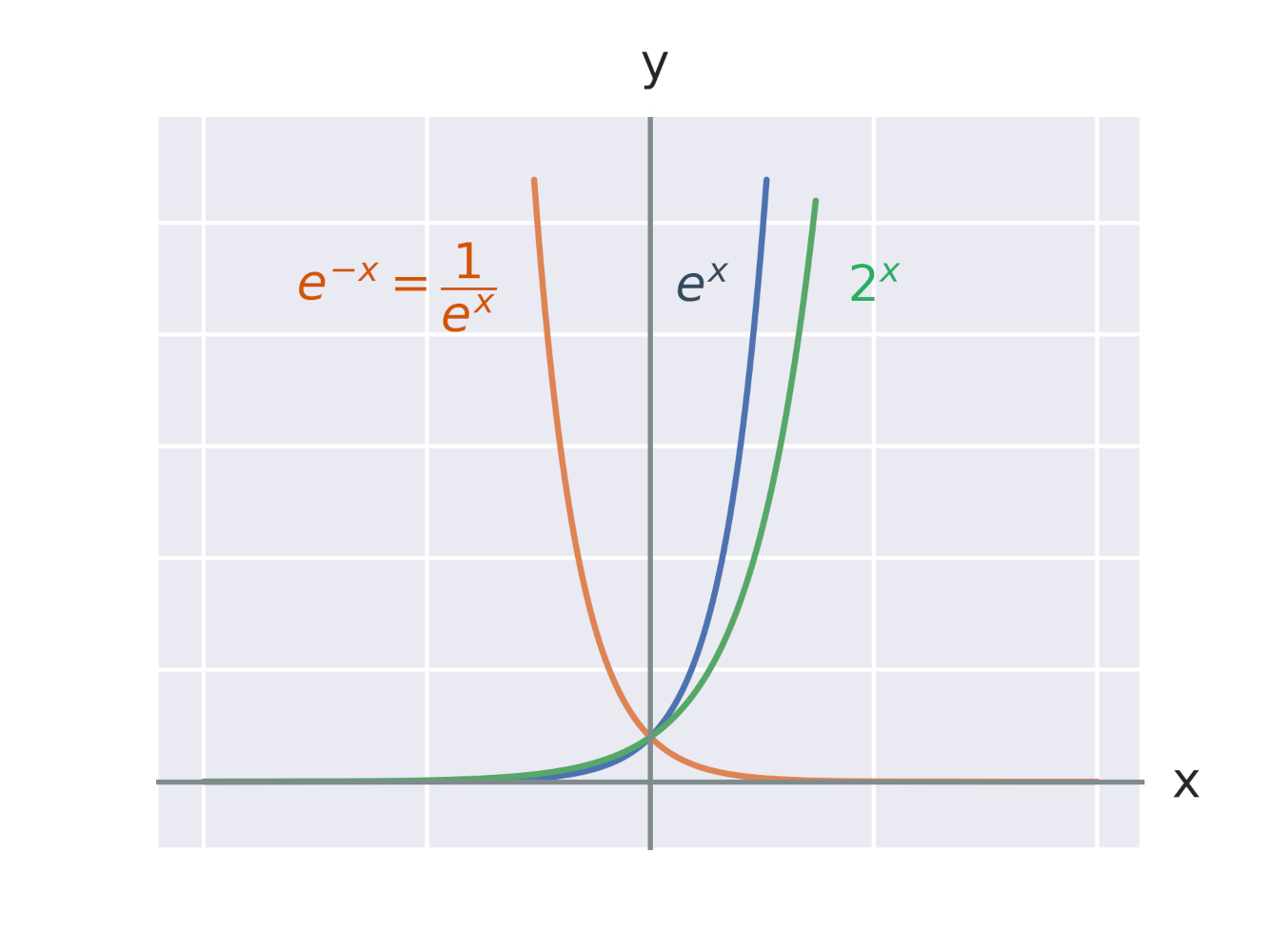
Grafom exponenciálnej funkcie je krivka s názvom exponenciála. Na obrázku sú grafy exponenciálnych funkcií so základmi 2 a e = 2{,}7 182 818 284\ldots. Vidíme tiež, že grafy funkcií e^x a e^{-x} sú spolu súmerné podľa osi y.
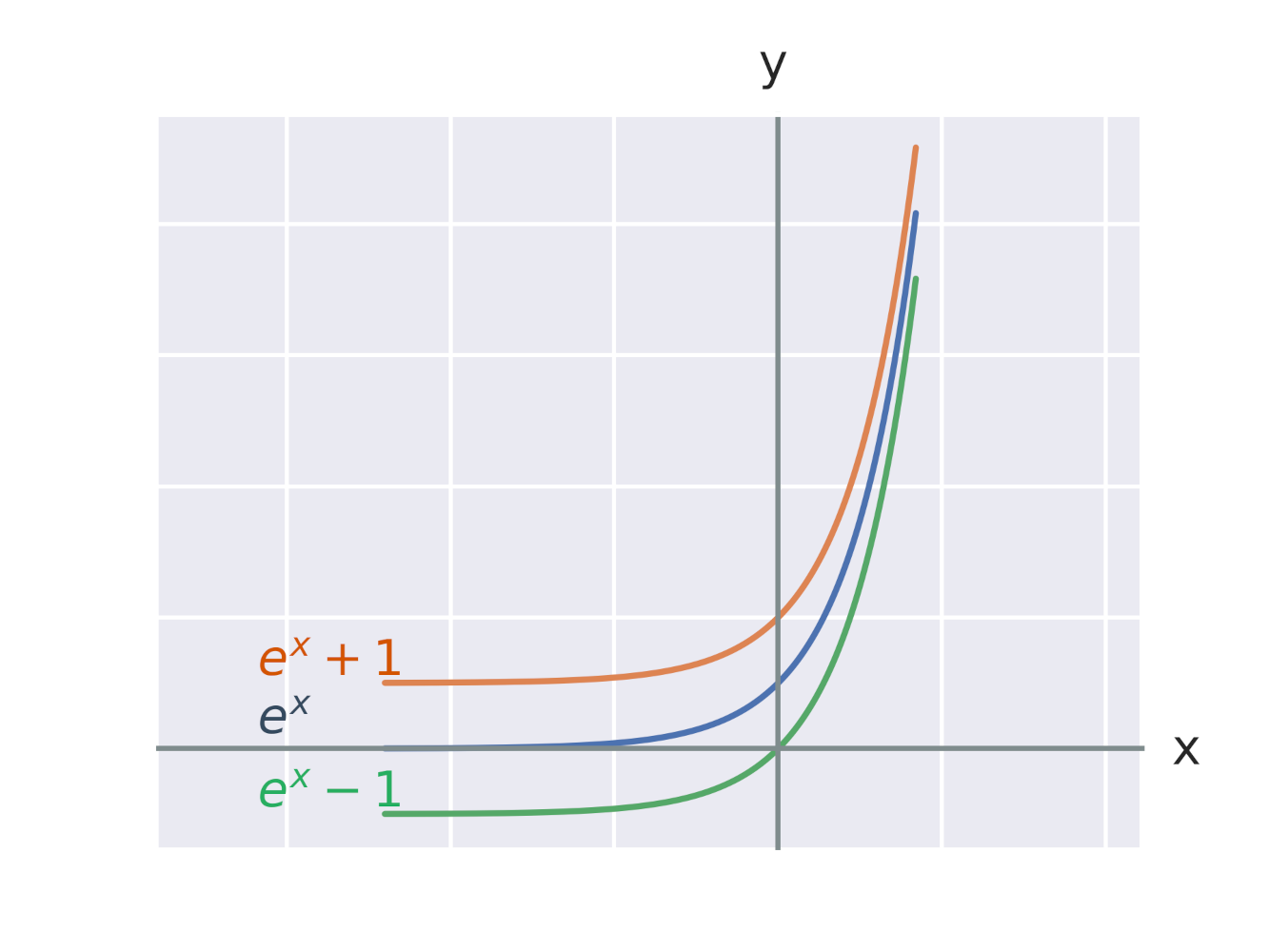
Efekt pripočítania konštanty k exponenciálnej funkcii
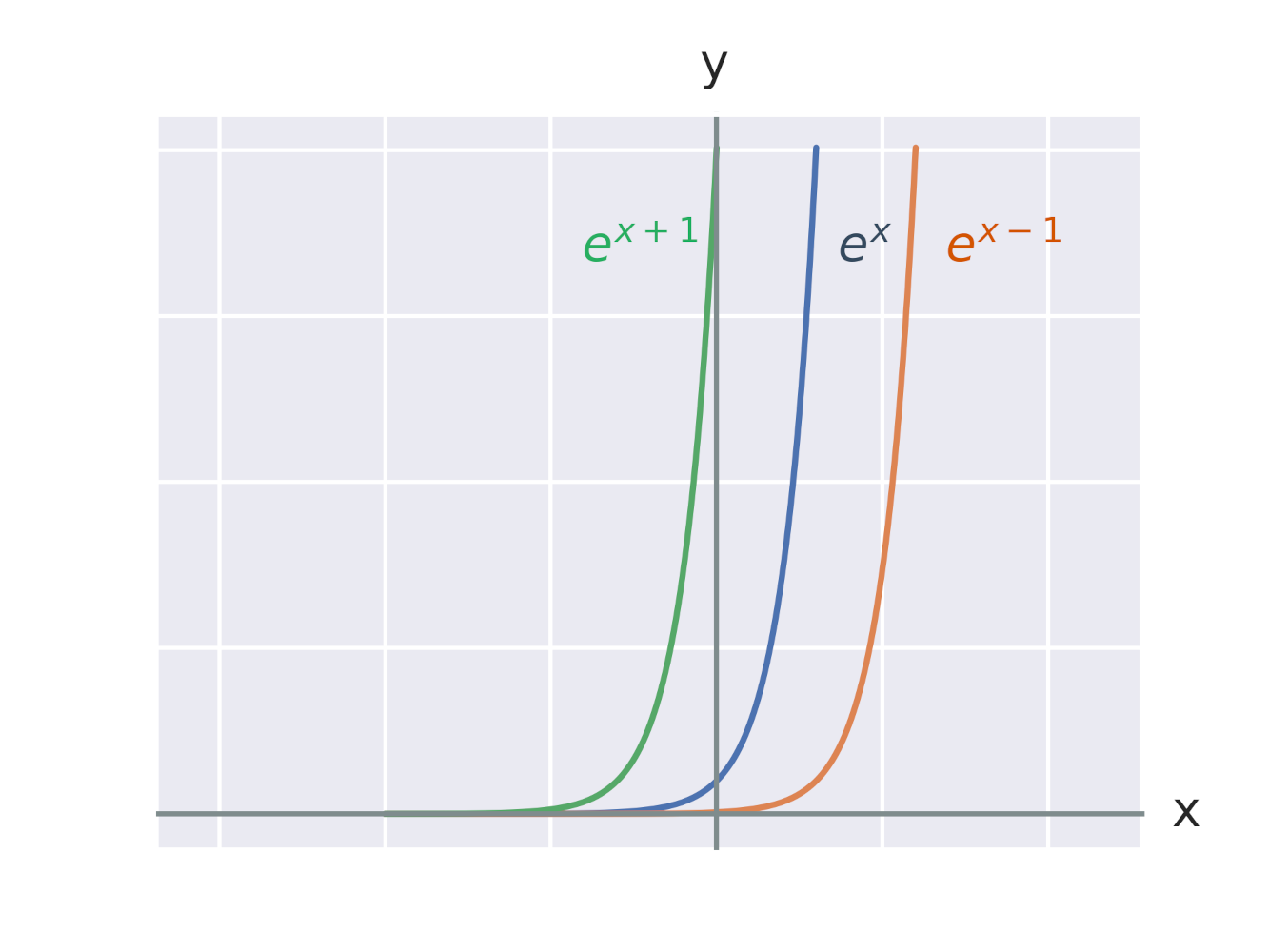
Efekt pripočítania konštanty k exponentu
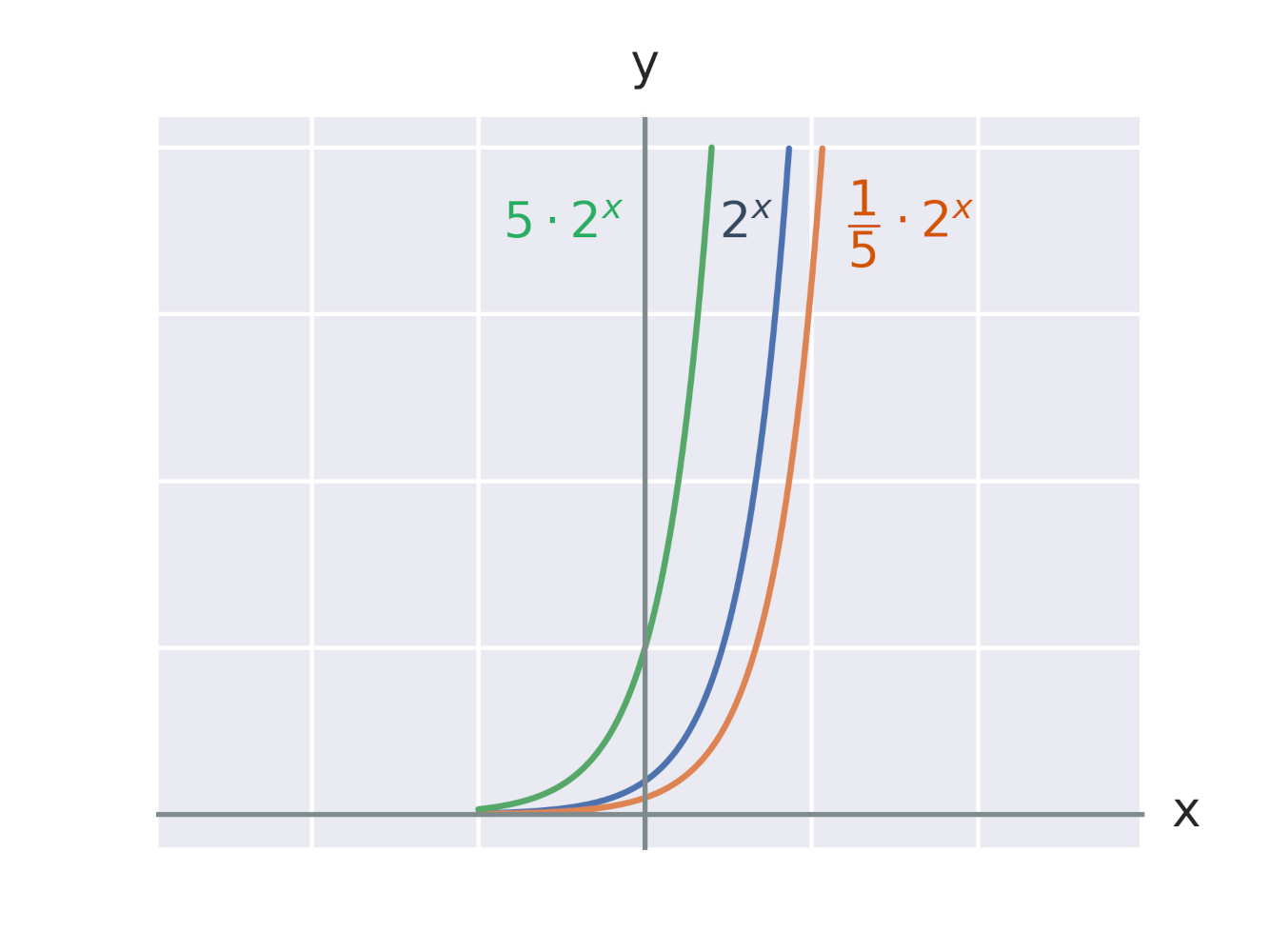
Efekt vynásobenia exponenciálnej funkcie konštantou
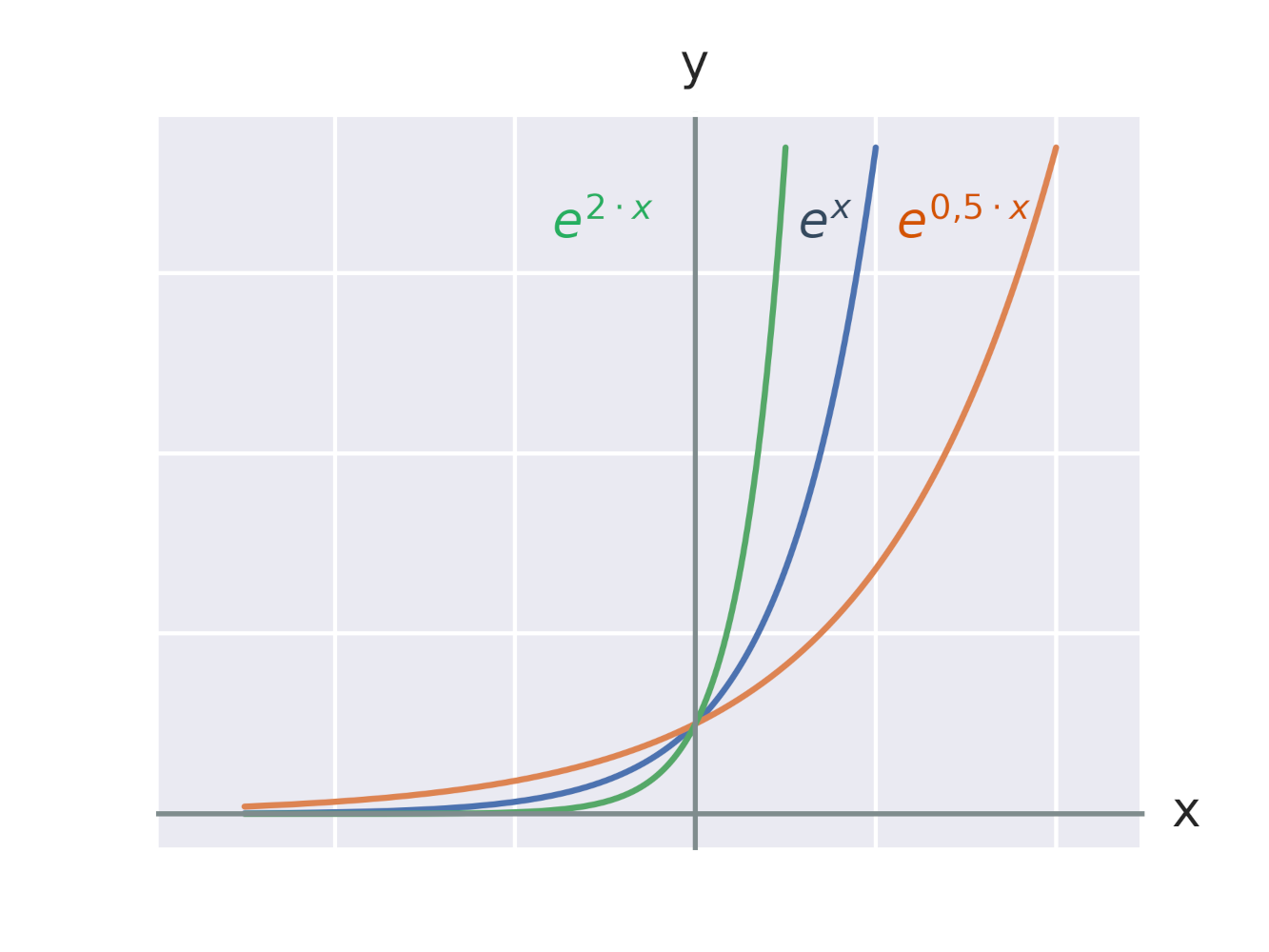
Efekt vynásobenia exponentu konštantou
Grafy logaritmických funkcií
Logaritmická funkcia je inverzná k exponenciálnej funkcii s rovnakým základom. Grafy dvoch navzájom inverzných funkcií sú osovo súmerné podľa osi prvého kvadrantu (teda priamky spĺňajúcej x=y).
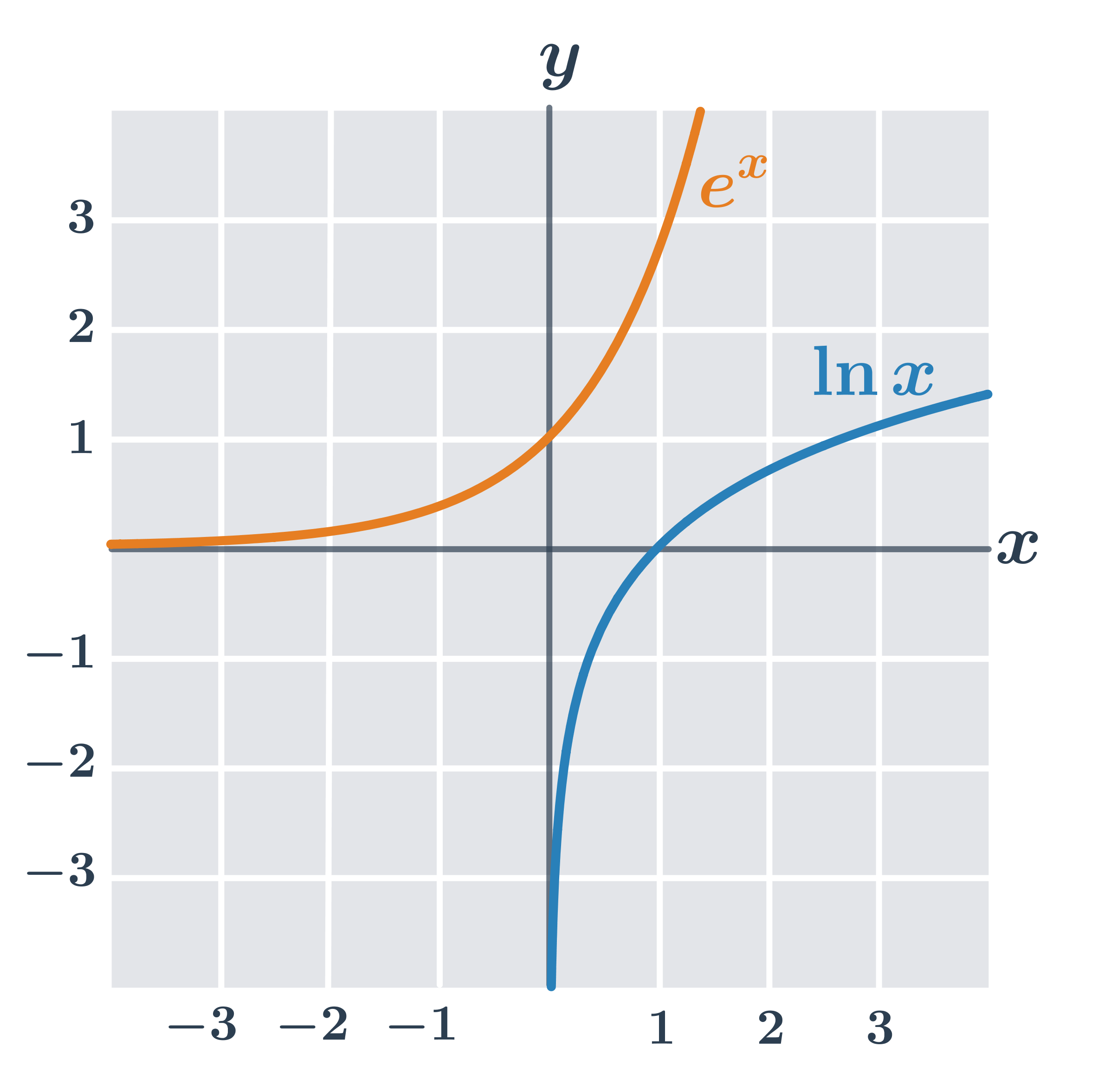
Na obrázku vidíme grafy logaritmických funkcií s rôznymi základmi 2, e, 10.
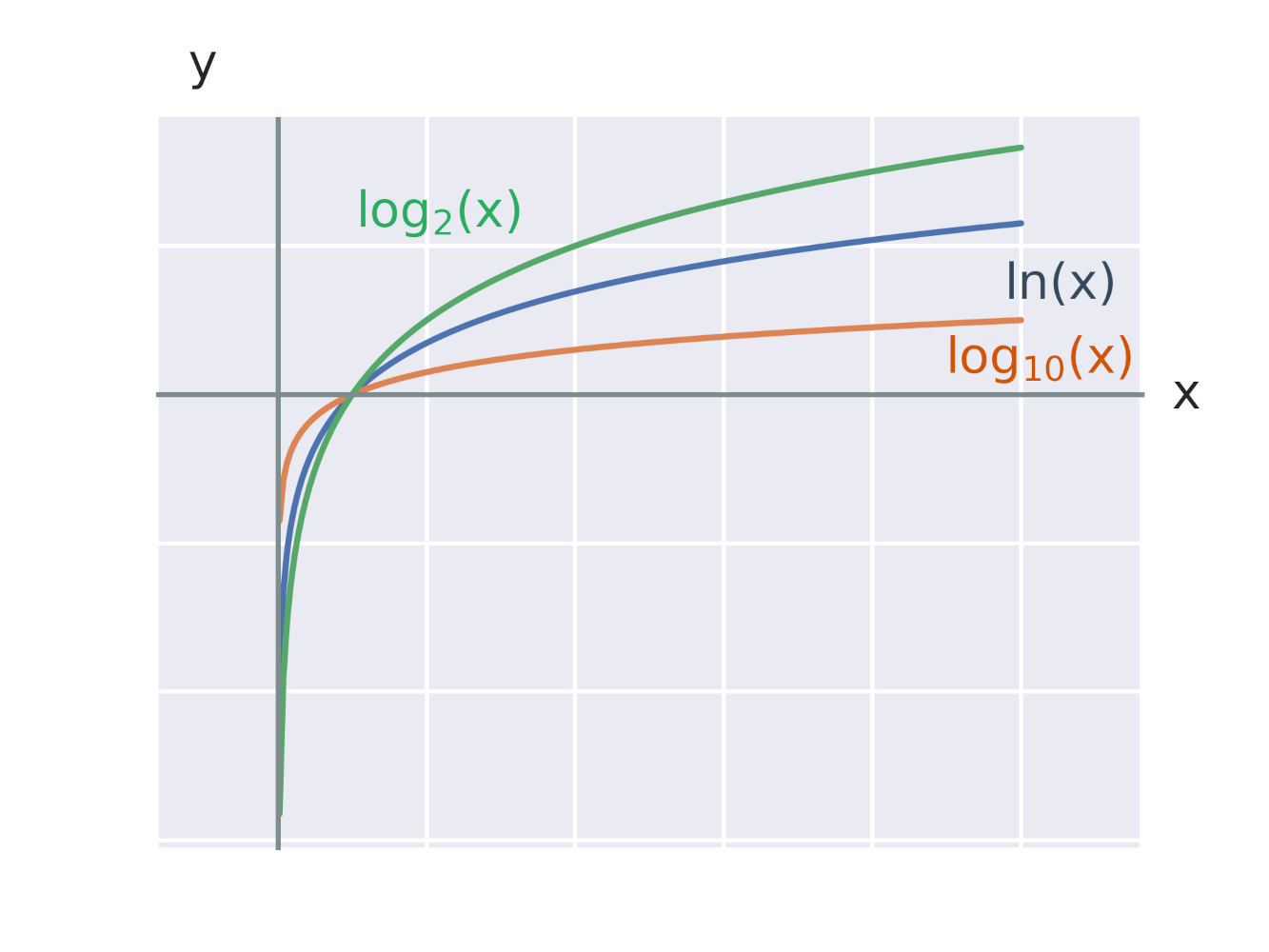
Značenie niektorých význačných logaritmických funkcií:
| funkcia | popis | značenie |
|---|---|---|
| \log_a x | všeobecne logaritmus x so základom a pre nejaké a >0, a\neq 1 | \log_a x |
| \log_e x | prirodzený logaritmus x | t u\ln x, v angl. textoch niekedy \log x |
| \log_{10} x | dekadický logaritmus x | tu \log x, v textoch slovenských aj angl. býva \log x, \log_{10}x |
| \log_2 x | binárny logaritmus x | tu \log_2 x, v textoch niekedy je aj \mathrm{lb}\;x |
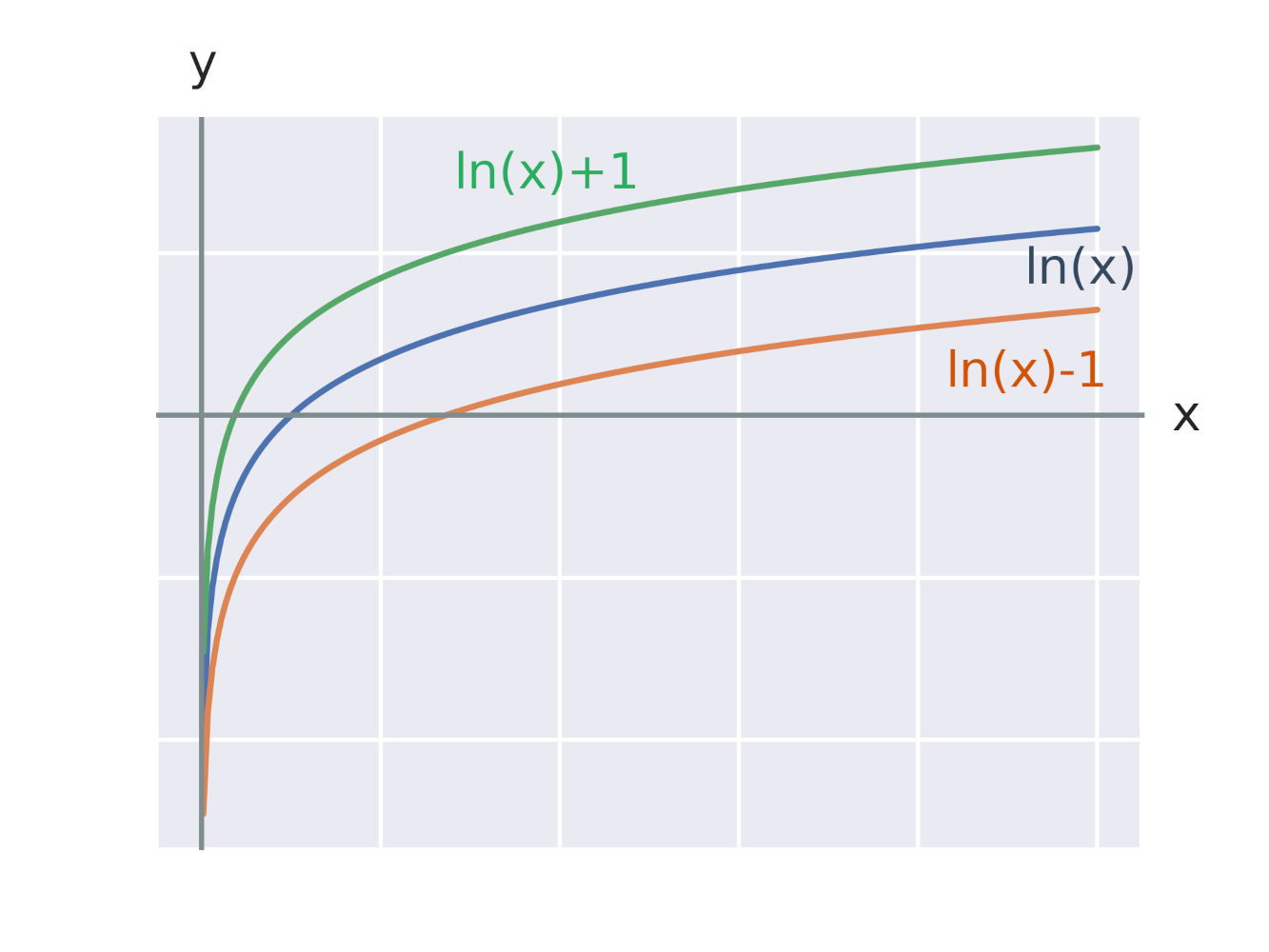
Efekt pripočítania konštanty k logaritmickej funkcii
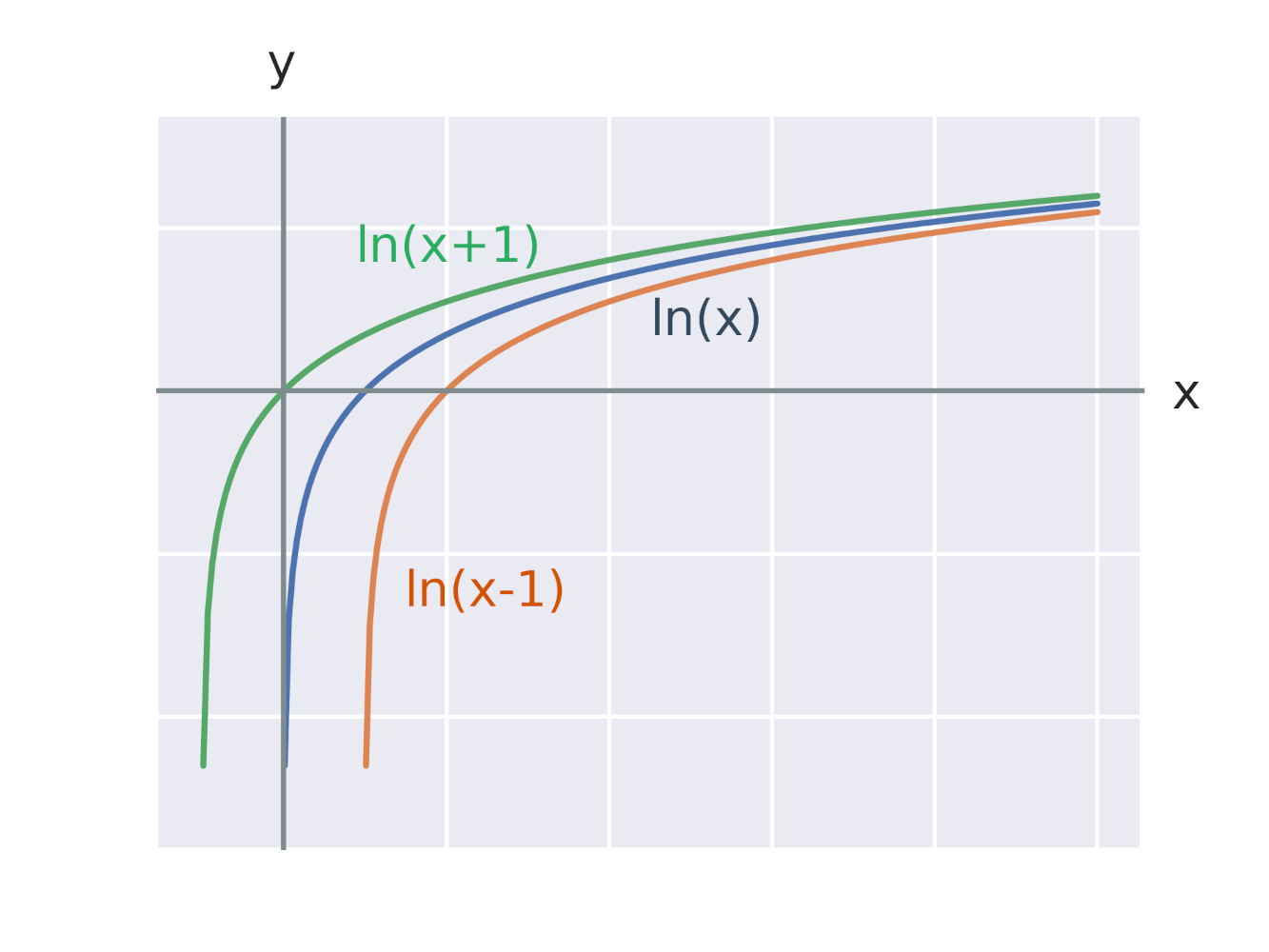
Efekt pripočítania konštanty k argumentu logaritmickej funkcie
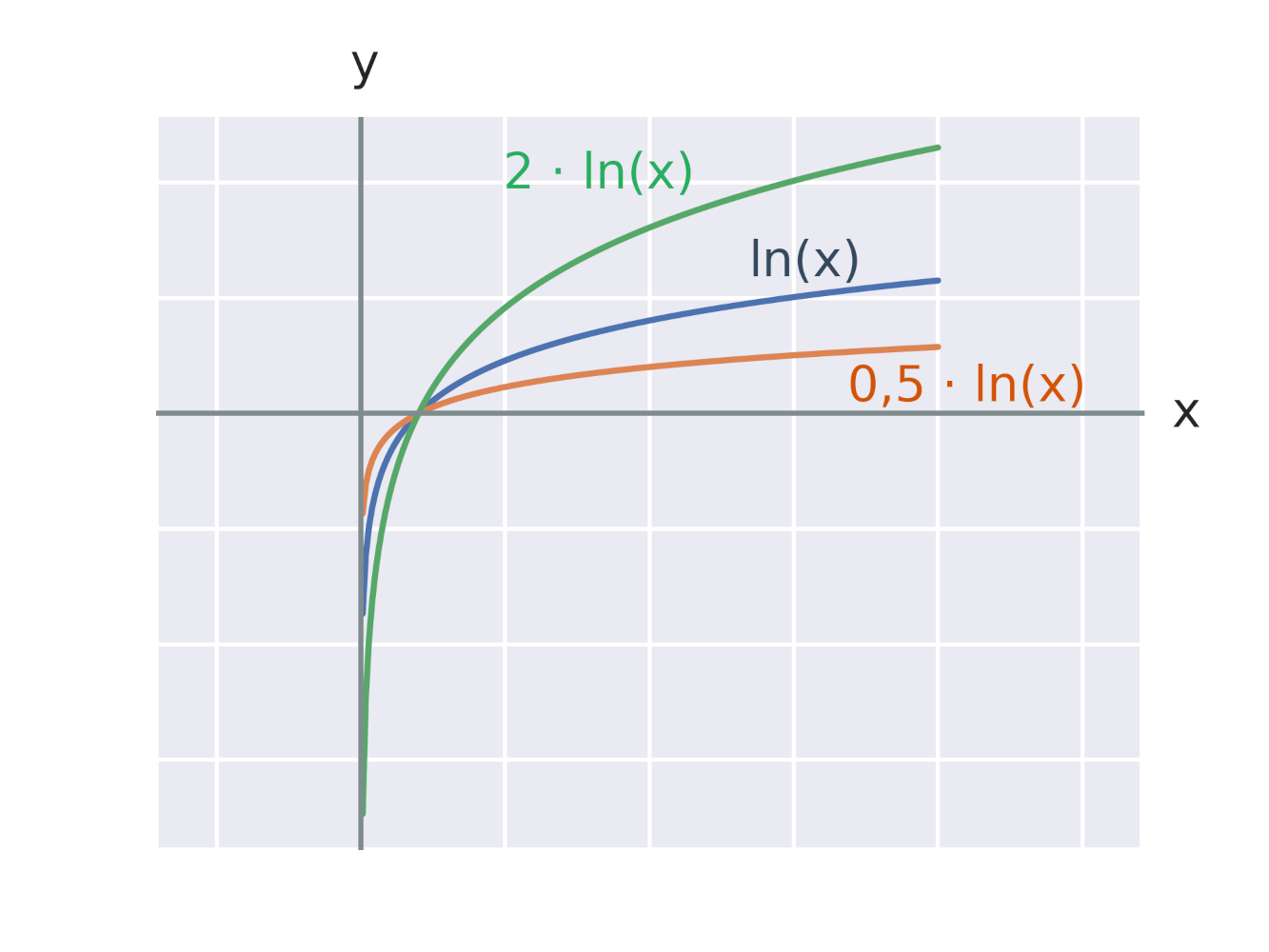
Efekt vynásobenia logaritmickej funkcie konštantou
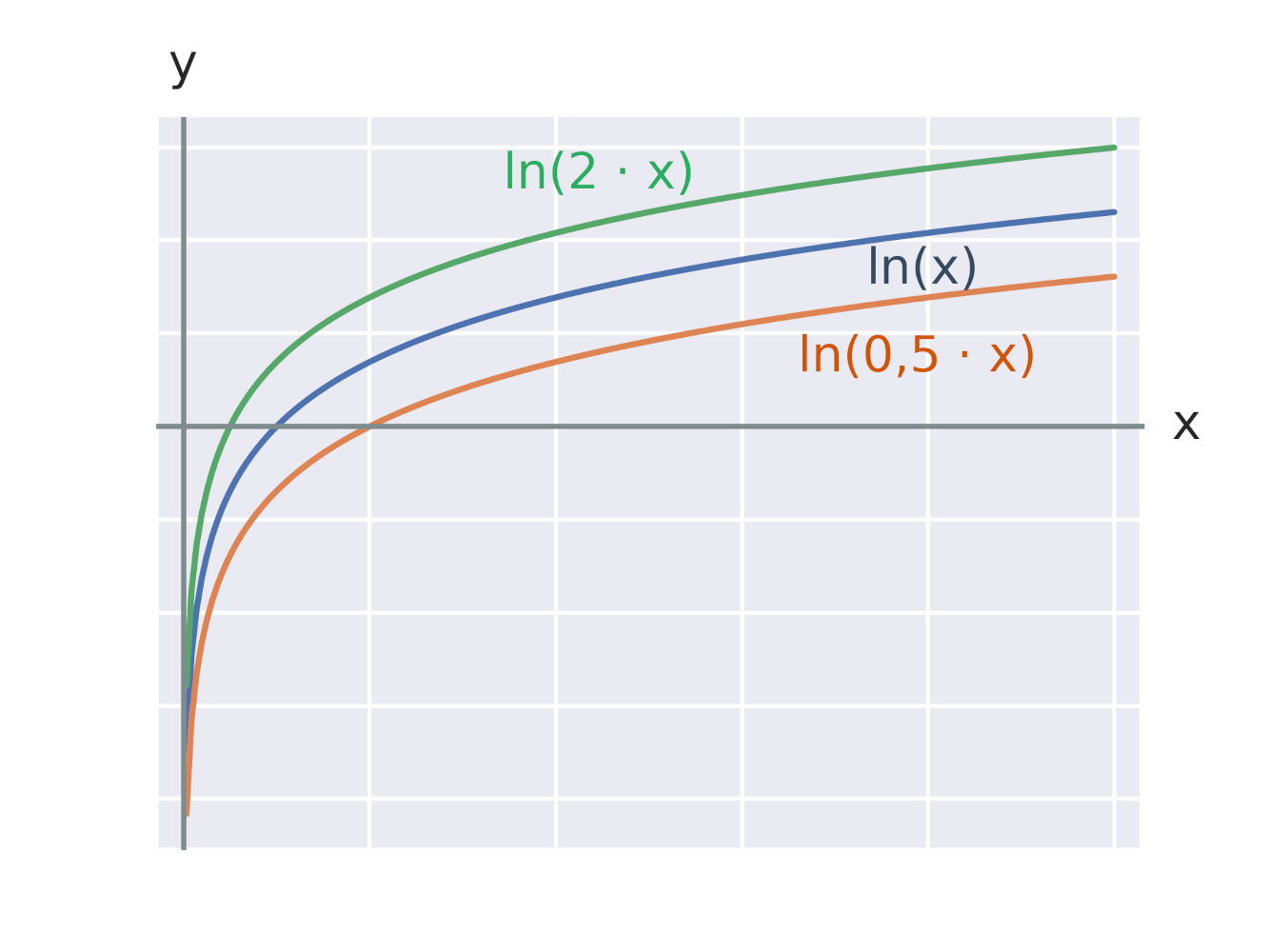
Efekt vynásobenie argumentu logaritmickej funkcie konštantou
Lineárne funkcie
Funkcia f je lineárna, ak ju je možné vyjadriť v tvare f(x) = a\cdot x + b, kde a a b sú konštanty. Grafom lineárnej funkcie je priamka. Parameter a je smernica (tiež nazývaná sklon), parameter b určuje jej zvislý posun (tiež nazývaný absolútny člen).
Príklady lineárnych funkcií:
- f(x) = 2x
- f(x) = -4x+8
- f(x) = \frac13 x + 1{,2}
Aby bola funkcia lineárna, nemusí byť nutne priamo zapísaná v tvare f(x) = a\cdot x + b. Stačí, keď ide na tento tvar upraviť. Príklady:
- f(x) = 2-x môžeme prepísať ako f(x)= -1x + 2, čo je lineárna funkcia so smernicou -1 a absolútnym členom 2.
- f(x) = 5(3-x) môžeme prepísať ako f(x)= -5x + 15, čo je lineárna funkcia so smernicou -5 a absolútnym členom 15.
- f(x) = x^2 + 7 - x(x-1) vyzerá na prvý pohľad ako kvadratická funkcia, ale môžeme ju upraviť na f(x)= x + 7 (kvadratický člen sa vyruší), takže ide o lineárnu funkciu.
Vlastnosti lineárnej funkcie
Funkcia f je lineárna, ak ju je možné vyjadriť v tvare f(x) = a\cdot x + b, kde a a b sú konštanty. Definičný obor lineárnej funkcie je celá množina reálnych čísel.
Špeciálnym prípadom lineárnej funkcie je funkcia konštantná. Tú dostávame v prípade, že a=0.
Ak a \neq 0, potom pre lineárnu funkciu platí:
- je jednoduchá,
- nie je obmedzená zhora ani zdola,
- nemá maximum ani minimum,
- nie je periodická,
- obor hodnôt je množina reálnych čísel.
Pre a>0 je funkcia f rastúca, pre a<0 je funkcia f klesajúca.
Pre b=0 je funkcia f nepárna.
Grafom lineárnej funkcie je priamka. Priesečník grafu s osou y je v bode (0, b). Priesečník grafu s osou x je v bode (-\frac{b}{a}, 0).
Kvadratické funkcie
Funkcia je kvadratická, keď ju môžeme vyjadriť v tvare f(x) = ax^2 + bx + c, kde a\neq 0. Funkcia je rýdzo kvadratická, ak nemá lineárny člen (teda b=0). Grafom kvadratickej funkcie je parabola. Kvadratická funkcia je špeciálny príklad polynómu (mnohočlena).
Príklady kvadratických funkcií:
- f(x) = x^2
- f(x) = (x+1)^2 = x^2 + 2x + 1
- f(x) = -3x^2 + 2x -8
Vlastnosti kvadratickej funkcie
Funkcia je kvadratická, ak ju je možné vyjadriť v tvare f(x) = ax^2 + bx + c, kde a\neq 0.
Definičný obor kvadratickej funkcie je celá množina reálných čísel.
Kvadratická funkcia nemá žiadnu z nasledujúcich vlastností: jednoduchá, periodická, rastúca, klesajúca.
Ďalšie vlastnosti závisia od toho, či je kvadratický člen kladný alebo záporný:
- Pre a>0 je funkcia zdola obmedzená, zhora nie je. V bode -\frac{b}{2a} má minimum.
- Pre a<0 je funkcia zhora obmedzená, zdola nie je. V bode -\frac{b}{2a} má maximum.
Goniometrické funkcie
Goniometrické funkcie (alebo tiež trigonometrické funkcie) sú funkcie, ktoré dávajú do vzťahu uhol v pravouhlom trojuholníku a pomer dvoch jeho strán. Goniometrické funkcie majú široké využitie v geometrii a veľa praktických aplikácií (napríklad v navigácii, nebeskej mechanike či geodézii). Goniometrické funkcie súvisia nie len s geometriou, ale aj s mnohými inými oblasťami matematiky. Môžeme sa s nimi stretnúť napríklad v prípade komplexných čísel či nekonečných radov.
Základné goniometrické funkcie sú sínus, kosínus a tangens. Ďalšie sú potom sekans, kosekans a kotangens.
Inverzné funkcie k funkciám goniometrickým sa nazývajú cyklometrické (napr.arkussínus, arkustangens).
Goniometrické funkcie a pravouhlý trojuholník
Goniometrické funkcie môžeme v pravouhlom trojuholníku vyjadriť nasledovne:
- Sínus (\sin) uhla \alpha je pomer dĺžky odvesny protiľahlej uhlu \alpha a dĺžky prepony.
- Kosínus (\cos) uhla \alpha je pomer dĺky odvesny priľahlej uhlu \alpha a dĺžky prepony.
- Tangens (\tan) uhla \alpha je pomer dĺžky odvesny protiľahlej uhlu \alpha a dĺžky odvesny priľahlej uhlu \alpha.
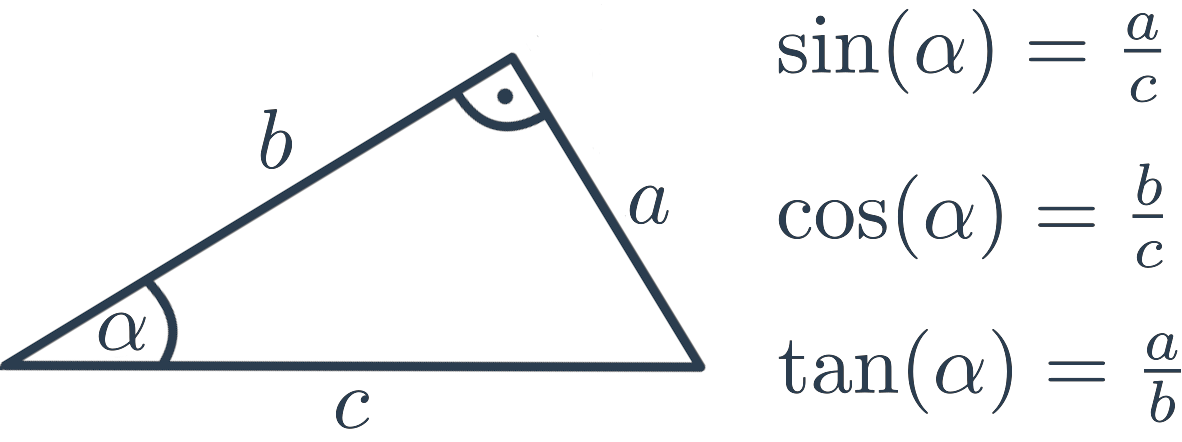
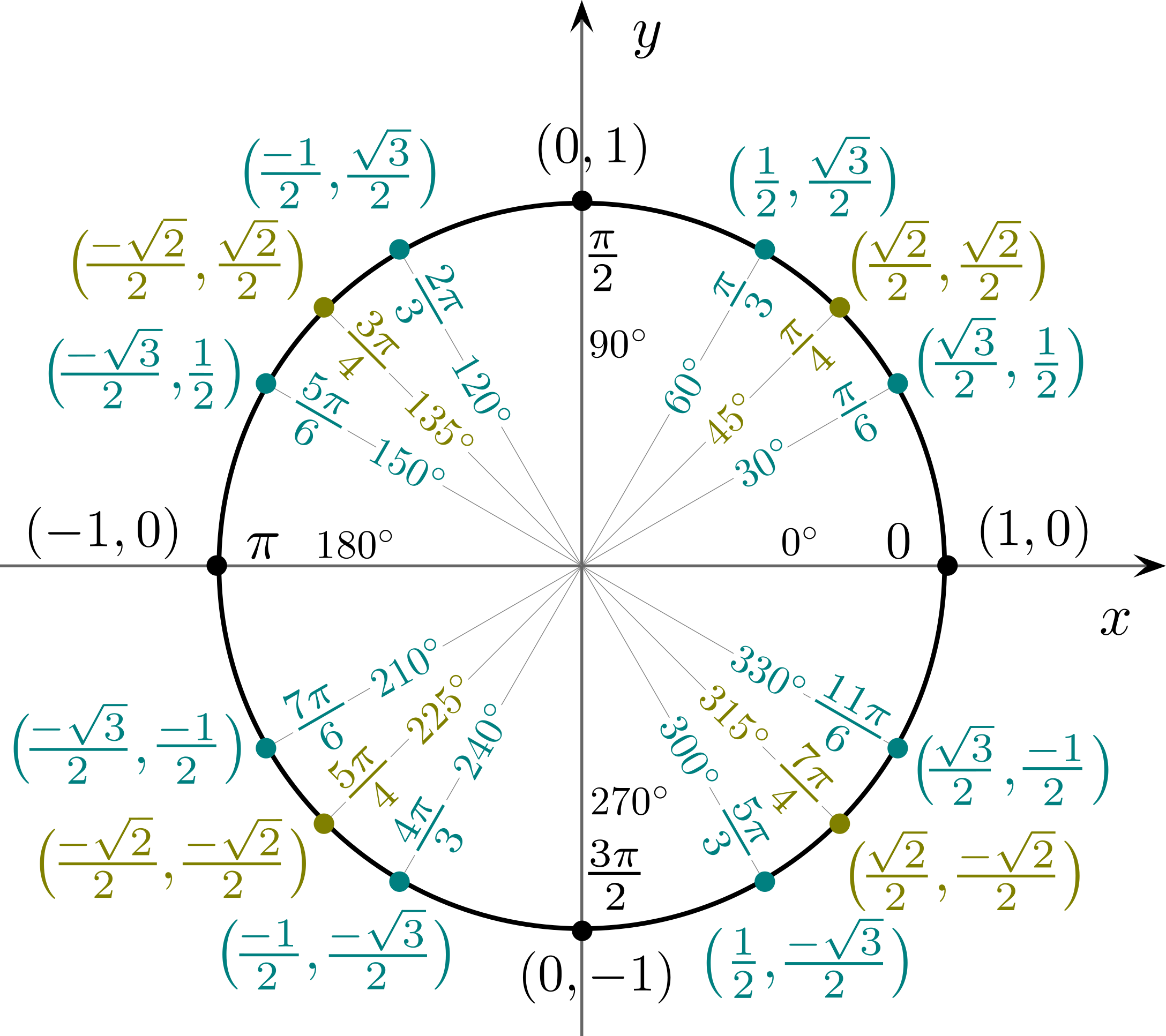
Hodnoty goniometrických funkcií
Často používané hodnoty goniometrických funkcií ilustruje tento obrázok jednotkovej kružnice – x-ová súradnica bodu zodpovedá hodnote \cos daného uhla, y-ová súradnica bodu zodpovedá hodnote \sin daného uhla.
Goniometrické funkcie: vzťahy a vzorce
Pre goniometrické funkcie platí celý rad vzťahov a vzorcov. Výber tých základných:
- Záporné hodnoty uhlov:
- \sin(-x) = -\sin(x) (nepárna funkcia)
- \cos(-x) = \cos(x) (párna funkcia)
- \tan(-x) = -\tan(x) (nepárna funkcia)
- Posuny:
- \sin(x+2\pi) = \sin(x) (perióda 2\pi)
- \sin(x+\pi) = -\sin(x)
- \sin(x+\frac{\pi}{2}) = \cos(x)
- Súčtové vzorce goniometrických funkcií:
- \sin(x+y) = \sin(x)\cos(y)+\cos(x)\sin(y)
- \sin(x-y) = \sin(x)\cos(y)-\cos(x)\sin(y)
- \cos(x+y) = \cos(x)\cos(y)-\sin(x)\sin(y)
- \cos(x-y) = \cos(x)\cos(y)+\sin(x)\sin(y)
- Dvojnásobný argument:
- \sin(2x) = 2\sin(x)\cos(x)
- \cos(2x) = \cos^2(x)-\sin^2(x)
- \tan(2x) = \frac{2\tan(x)}{1-\tan^2(x)}
Vlastnosti goniometrických funkcií
Pre obe funkcie \sin(x) a \cos(x) platí:
- definičný obor je množina reálnych čísel,
- obor hodnôt je interval \langle -1, 1 \rangle,
- funkcia je obmedzená,
- funkcia je periodická s periódou 2\pi,
- funkcia nie je prostá.
Pre funkciu \sin(x) platí:
- je nepárna,
- nulové hodnoty nadobúda v bodoch x=k\pi.
Pre funkciu \cos(x) platí:
- je párna,
- nulové hodnoty nadobúda v bodoch x=(2k+1)\frac{\pi}{2}.
Pre funkciu \tan(x) platí:
- definičný obor je \{x \in \mathbb{R}: x \neq (2k+1)\frac{\pi}{2} \},
- obor hodnôt je množina reálnych čísel,
- funkcia je nepárna,
- funkcia je periodická s periódou \pi,
- funkcia je neobmedzená,
- nulové hodnoty nadobúda v bodoch x=k\pi.


 Slovenčina
Slovenčina Angličtina
Angličtina Informatika
Informatika Vieme to
Vieme to Nemčina
Nemčina Biológia
Biológia Zemepis
Zemepis Chémia
Chémia
