Geometria
Nárys, pôdorys, bokorys
Nárys, bokorys a pôdorys sa používajú k dvojrozmernému zakresleniu trojrozmerného objektu pomocou pravouhlého premietania. Každý z nich zachycuje pohľad na objekt z iného smeru:
- Nárys je pohľad z prednej strany.
- Bokorys je pohľad z bočnej strany.
- Pôdorys je pohľad zhora.
Počty vrcholov, strán, hrán
Pre počet vrcholov v, hrán h a stien s konvexného mnohostenu platí Eulerova veta: v - h + s = 2.
Počty vrcholov, stien a hrán pre pravidelné mnohosteny:
| mnohosten | počet stien | počet vrcholov | počet hrán |
|---|---|---|---|
| štvorsten | 4 | 4 | 6 |
| kocka | 6 | 8 | 12 |
| osemsten | 8 | 6 | 12 |
| dvanásťsten | 12 | 20 | 30 |
| dvadsaťsten | 20 | 12 | 30 |
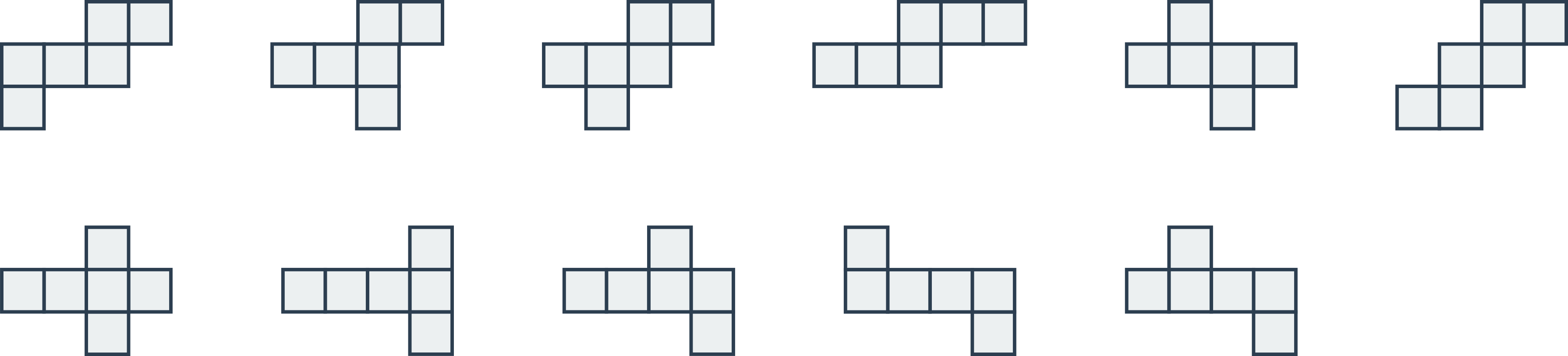
Sieť kocky
Sieť kocky môžeme zakresliť 11 rôznymi spôsobmi:
Siete telies
Sieť telesa je rovinné zakreslenie, z ktorého je možné poskladať plášť telesa. Príklady sietí:
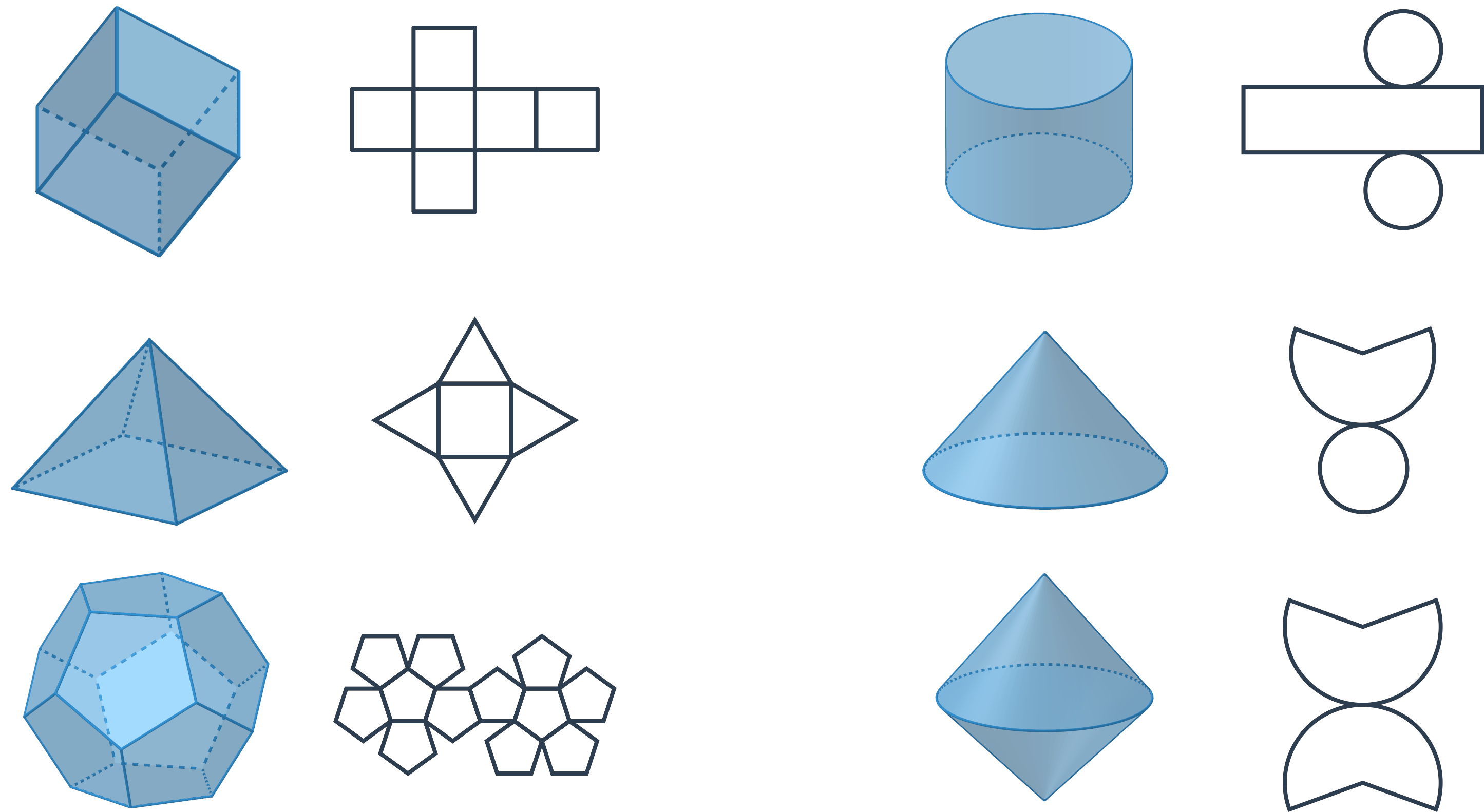
Sieť telesa je väčšinou možné zakresliť mnohými rôznymi spôsobmi. Sieť kocky môžeme zakresliť takto:

Geometrické pojmy
Na rozdiel od bežného jazyka, kde majú slová väčšinou niekoľko významov, v matematike používáme pojmy s presne definovaným významom. To je veľmi užitočné, pretože sa vďaka tomu môžeme vyjadrovať stručne a pritom jednoznačne. V geometrii sa využíva celý rad pojmov.
| téma | príklady pojmov |
|---|---|
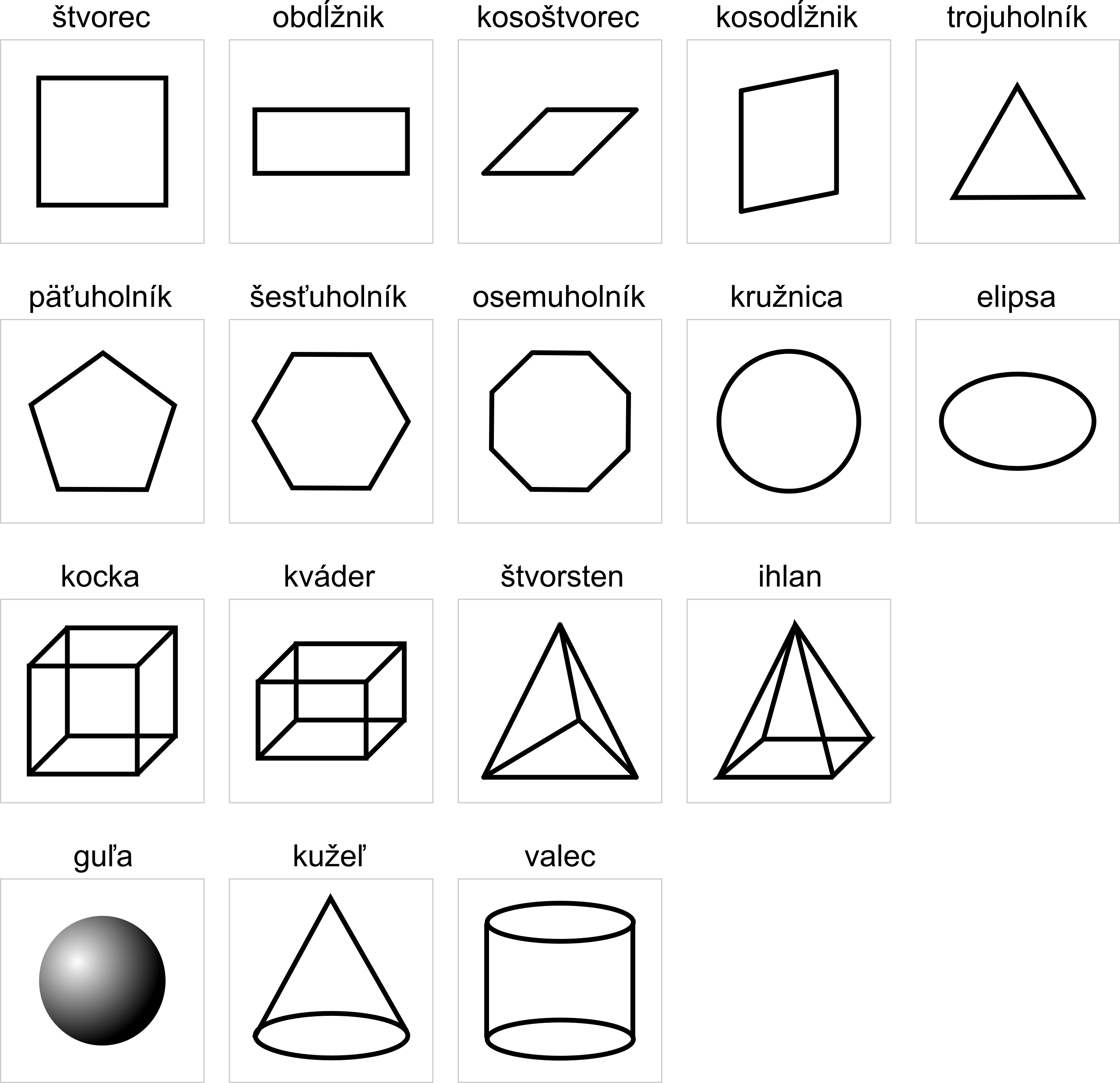
| Názvy geometrických útvarov a telies | obdĺžnik, kosodĺžnik, trojuholník, kružnica, kocka, kváder, ihlan, guľa |
| Pojmy súvisiace s uhlami | uhol tupý, ostrý, pravý, plný, striedavý, vrcholový |
| Pojmy súvisiace s trojuholníkom | ťažisko, výška, prepona, odvesna, kružnica vpísaná, rovnoramenný trojuholník |
| Pojmy súvisiace s kružnicou | priemer, polomer, tetiva, dotyčnica, sečnica, výsek, odsek, stredový uhol |
| Kuželosečky: pojmy | elipsa, hyperbola, parabola, os, vrchol, stred, asymptota |
Názvy útvarov
Pojmy súvisiace s uhlami
| plný uhol | uhol s veľkosťou 360° |
| priamy uhol | uhol s veľkosťou 180° |
| pravý uhol | uhol s veľkosťou 90° |
| ostrý uhol | uhol menší než 90° |
| tupý uhol | uhol väčší než 90° a menší než 180° |
| konvexný uhol | uhol menší alebo rovný 180° |
| nekonvexný, konkávny uhol | uhol väčší než 180° |
| vrcholové uhly | dvojice uhlov, ktorých ramená sú opačné polpriamky |
| vedľajšie uhly | dvojice uhlov, ktorých jedno rameno je spoločné a druhé ramená sú opačné polpriamky |
| súhlasné uhly | dvojice uhlov, ktorých prvé ramená ležia na jednej priamke a druhé ramená sú rovnobežné, pritom smer príslušných ramien je rovnaký |
| striedavé uhly | dvojice uhlov, ktorých prvé ramená ležia na jednej priamke a druhé ramená sú rovnobežné, pritom smer príslušných ramien je opačný |
Pojmy súvisiace s trojuholníkom
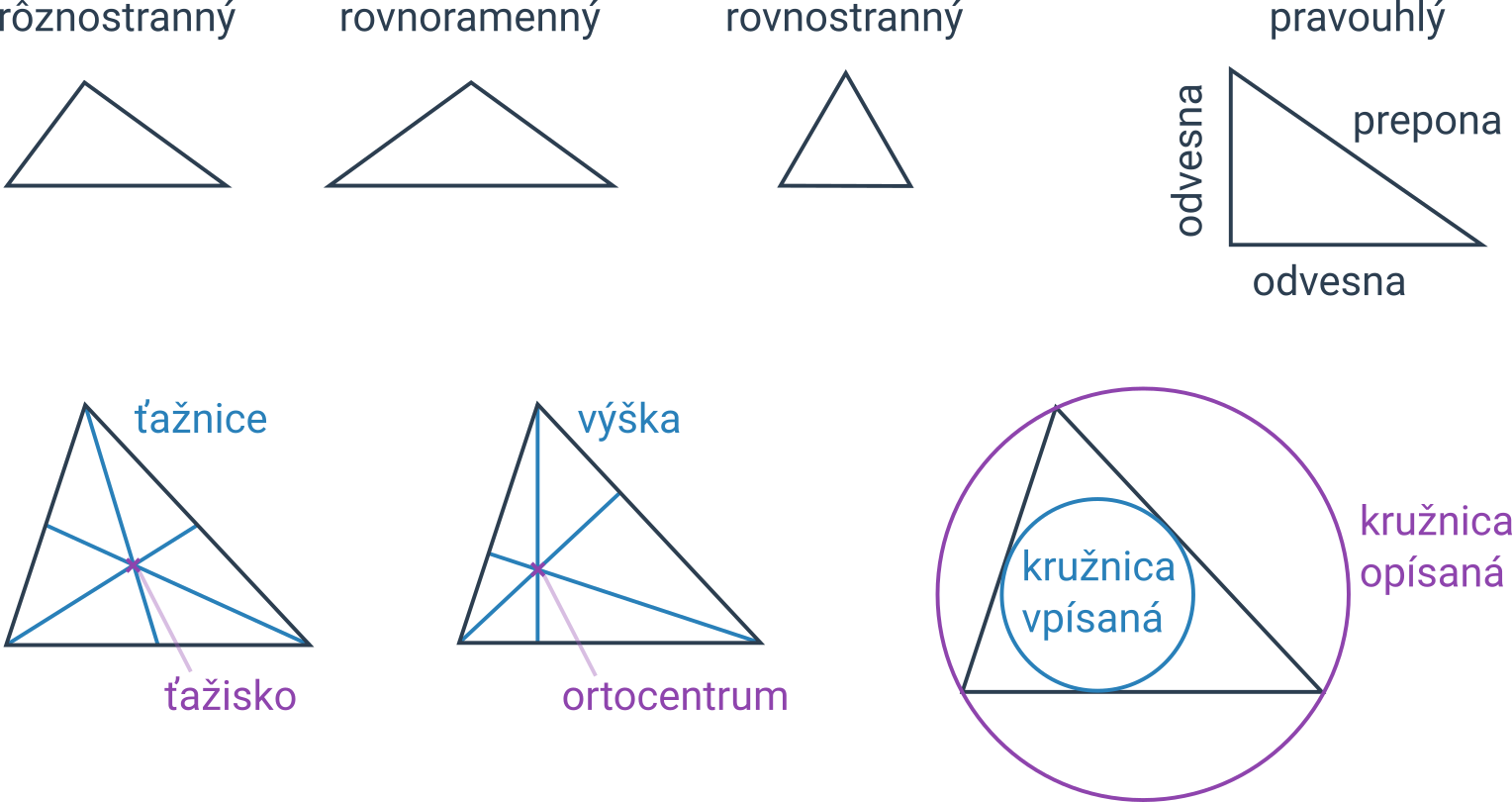
| všeobecný (rôznostranný) trojuholník | trojuholník, v ktorom nie sú žiadne dve strany zhodné |
| rovnoramenný trojuholník | trojuholník, ktorý má dve strany zhodné |
| rovnostranný trojuholník | trojuholník, ktorý má všetky tri strany zhodné |
| pravouhlý trojuholník | trojuholník, ktorý má jeden uhol pravý |
| odvesna | strana susediaca s pravým uhlom v pravouhlom trojuholníku |
| prepona | strana protiľahlá k pravému uhlu v pravouhlom trojuholníku |
| ťažnica | úsečka spájajúca stred strany a protiľahlý vrchol trojuholníka |
| ťažisko | priesečník ťažníc |
| výška | úsečka spájujúca vrchol trojuholníka a pätu kolmice vedenej týmto vrcholom na protiľahlú stranu |
| ortocentrum | priesečník výšok |
| opísaná kružnica | kružnica, ktorá prechádza všetkými vrcholmi trojuholníka |
| vpísaná kružnica | kružnica, ktorá sa dotýká všetkých strán trojuholníka |
| stred opísanej kružnice | priesečník osí strán |
| stred vpísanej kružnice | priesečník osí uhlov |
Pozn. Presné definície rovnoramenného trojuholníka sa líšia: niektorí autori vyžadujú „aspoň“ dve strany zhodné, iní „presne“ dve strany zhodné. Rozdiel je v tom, či rovnostranné trojuholníky považujeme za rovnoramenné.
Pojmy súvisiace s kružnicou
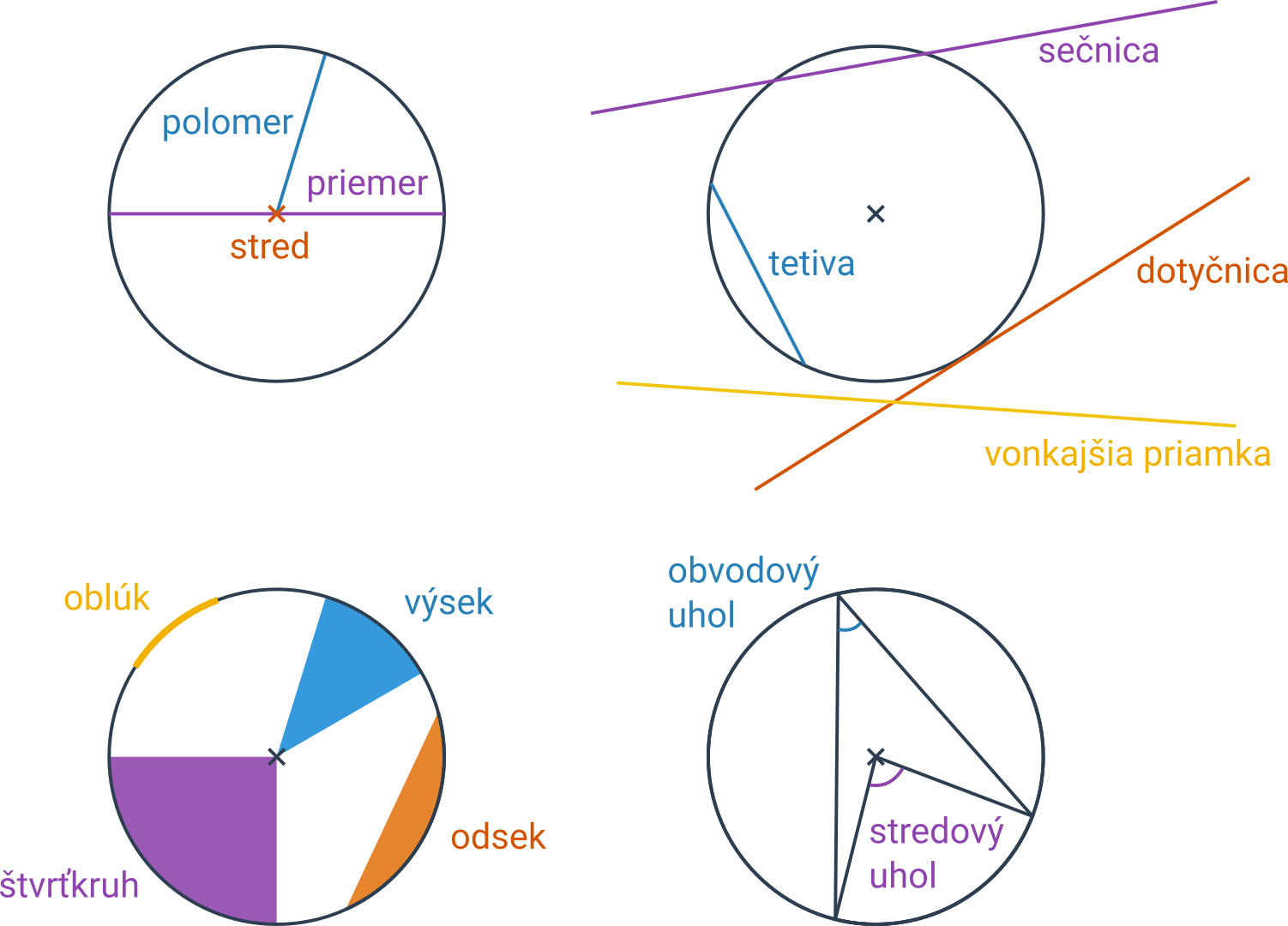
| polomer | úsečka, ktorej jeden koncový bod leží na kružnici a druhý koncový bod v strede kružnice |
| priemer | úsečka, ktorá prechádza stredom kružnice a ktorej oba krajné body ležia na tejto kružnici |
| dotyčnica | priamka, ktorá sa kružnice dotýka presne v jednom bode |
| sečnica | priamka, ktorá kružnicu pretína v dvoch bodoch |
| vonkajšia priamka | priamka, ktorá kružnicu nepretína |
| tetiva | úsečka spájajúca dva body na kružnici |
| kruhová výseč | časť kruhu príslušná stredovému uhlu |
| medzikružie | plocha medzi dvomi sústrednými kružnicami |
| polkruh | výseč príslušná priamemu uhlu (180°) |
| štvrťkruh | výseč príslušná pravému úhlu (90°) |
| odsek | časť kruhu vymedzená tetivou a kruhovým oblúkom vzniknutá rozdelením kruhu sečnicou |
| stredový uhol | uhol, ktorého vrcholom je stred kružnice a ktorého ramená prechádzajú krajnými bodmi oblúka |
| obvodový uhol | uhol, ktorého vrchol leží na kružnici a ramená prechádzajú krajnými bodmi oblúka |
Pytagorova veta
Pytagorova veta popisuje vzťah, ktorý platí medzi dĺžkami strán pravouhlého trojuholníka. Veta znie: Obsah štvorca zostrojeného nad preponou pravouhlého trojuholníka je rovný súčtu obsahov štvorcov nad obomi jeho odvesnami. Pytagorovu vetu môžeme zapísať vzťahom c^2 = a^2 + b^2, kde c označuje dĺžku prepony pravouhlého trojuholníka a dĺžky odvesien sú a, b.
Nasledujúci obrázok znázorňuje graficky znenie vety a tiež „obrázkový dôkaz“ tejto vety:
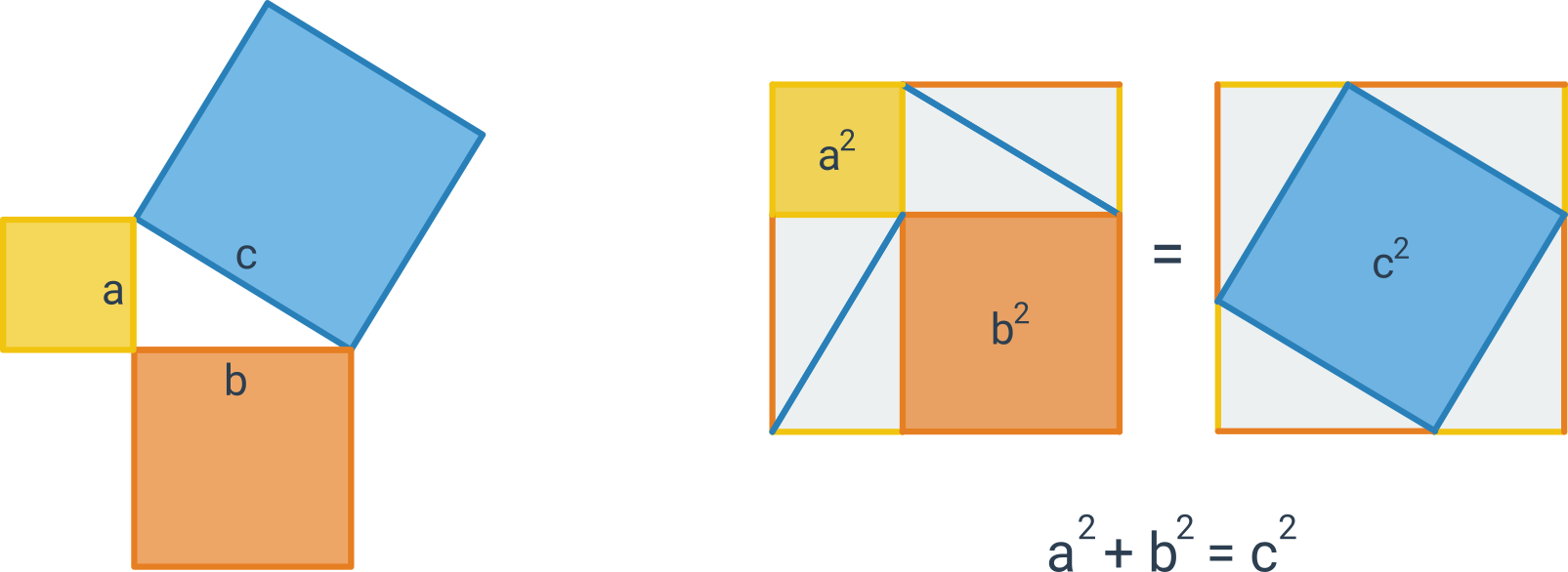
Platí aj opačný smer: Ak má trojuholník strany dĺžok a, b, c, ktoré spĺňajú rovnosť c^2 = a^2 + b^2, potom musí ísť o pravouhlý trojuholník s preponou c.
Pytagorova veta: základné použitie
Pytagorova veta umožňuje dopočítať dĺžku tretej strany pravouhlého trojuholníka, pri ktorom poznáme dĺžky dvoch zvyšných strán:
Dĺžka odvesny c = \sqrt{a^2 + b^2}. Ak má pravouhlý trojuholník odvesny s dĺžkou 3 metre a 6 metrov, prepona má dĺžku \sqrt{3^2+6^2} = \sqrt{9+36} = \sqrt{45} \doteq 6,41 metra.
Dĺžka prepony a = \sqrt{c^2-b^2}. Ak má trojuholník preponu s dĺžkou 8 metrov a jedna z odvesien má dĺžku 4 metre, druhá odvesna má dĺžku \sqrt{8^2-4^2} = \sqrt{64-16} = \sqrt{48} \doteq 6,93 metra.
Pytagorejské trojice sú trojice celých čísel, ktoré spĺňajú a^2+b^2=c^2, teda trojuholník s príslušnými dĺžkami strán je pravouhlý. Typickým príkladom pytagorejskej trojice je (3, 4, 5): 3^2 + 4^2 = 9+16 = 25 = 5^2.
Ďalšie príklady pytagorejských trojíc: (5, 12, 13); (8, 15, 17); (7, 24, 25); (20, 21, 29); (9, 40, 41). Medzi pytagorejské trojice patria tiež všetky násobky týchto trojíc, napr. (6, 8, 10); (9, 12, 15); (10, 24, 26). Ak si zapamätáme niektoré základné pytagorejské trojice, predovšetkým najjednoduchšiu trojicu (3, 4, 5), tak nám to môže uľahčiť výpočty.
Pytagorova veta: aplikácie
Pytagorova veta má v geometrii veľmi široké využitie, pretože môžeme veľa zložitejších útvarov rozložiť na pravouhlé trojuholníky.
Typickým príkladom aplikácie Pytagorovej vety je výpočet dĺžky uhlopriečky štvorca alebo výšky rovnostranného trojuholníka:
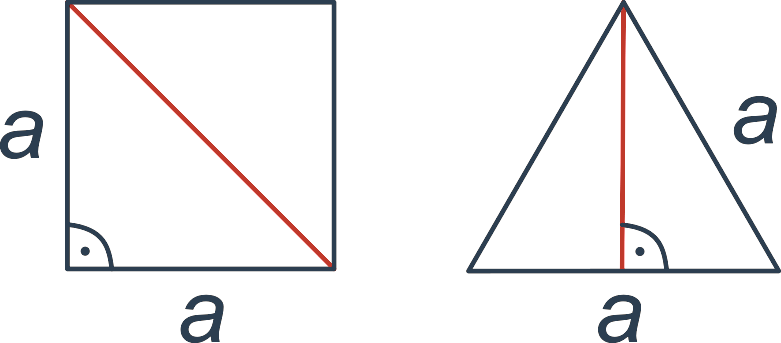
V prípade štvorca so stranou a tvorí uhlopriečka preponu pravouhlého trojuholníka s odvesnami s dĺžkou a. Pre dĺžku uhlopriečky u teda platí u^2 = a^2 + a^2. Po úpravách: u = \sqrt{a^2+a^2} = \sqrt{2a^2} = a\sqrt{2}. Napríklad štvorec so stranou 10 cm má teda uhlopriečku s dĺžkou 10\cdot \sqrt{2} \doteq 14,1 metra.
V prípade rovnostranného trojuholníka so stranou a tvorí výška odvesnu pravouhlého trojuholníka s preponou s dĺžkou a a odvesnou s dĺžkou \frac{a}{2}. Pre dĺžku výšky v teda platí v^2 + \large(\frac{a}{2}\large)^2 = a^2. Po úpravách dostávame v^2 = a^2 - \frac{a^2}{2^2} = \frac{3}{4}a^2, v = a\frac{\sqrt{3}}{2}. Napríklad v rovnostrannom trojuholníku so stranou 5 metrov má teda výška dĺžku \frac{\sqrt{3}}{2}\cdot 5 \doteq 4,33 metra.
Euklidove vety
Euklidove vety sú dve tvrdenia o vlastnostiach pravouhlého trojuholníka.
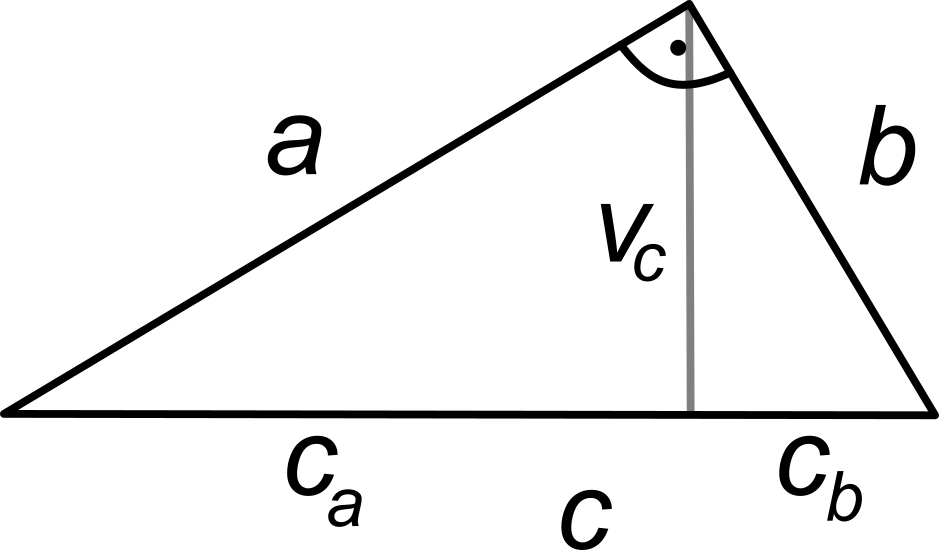
Euklidova veta o výške
Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z oboch úsekov prepony:
v_c^2 = c_a\cdot c_b
Euklidova veta o odvesne
Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z prepony a úseku prepony priľahlej k tejto odvesne.
- a^2 = c\cdot c_a
- b^2 = c\cdot c_b
Lichobežník
Lichobežník je štvoruholník, ktorého dve protiľahlé strany sú rovnobežné (hovoríme im základne) a zvyšné dve protiľahlé strany sú rôznobežné.
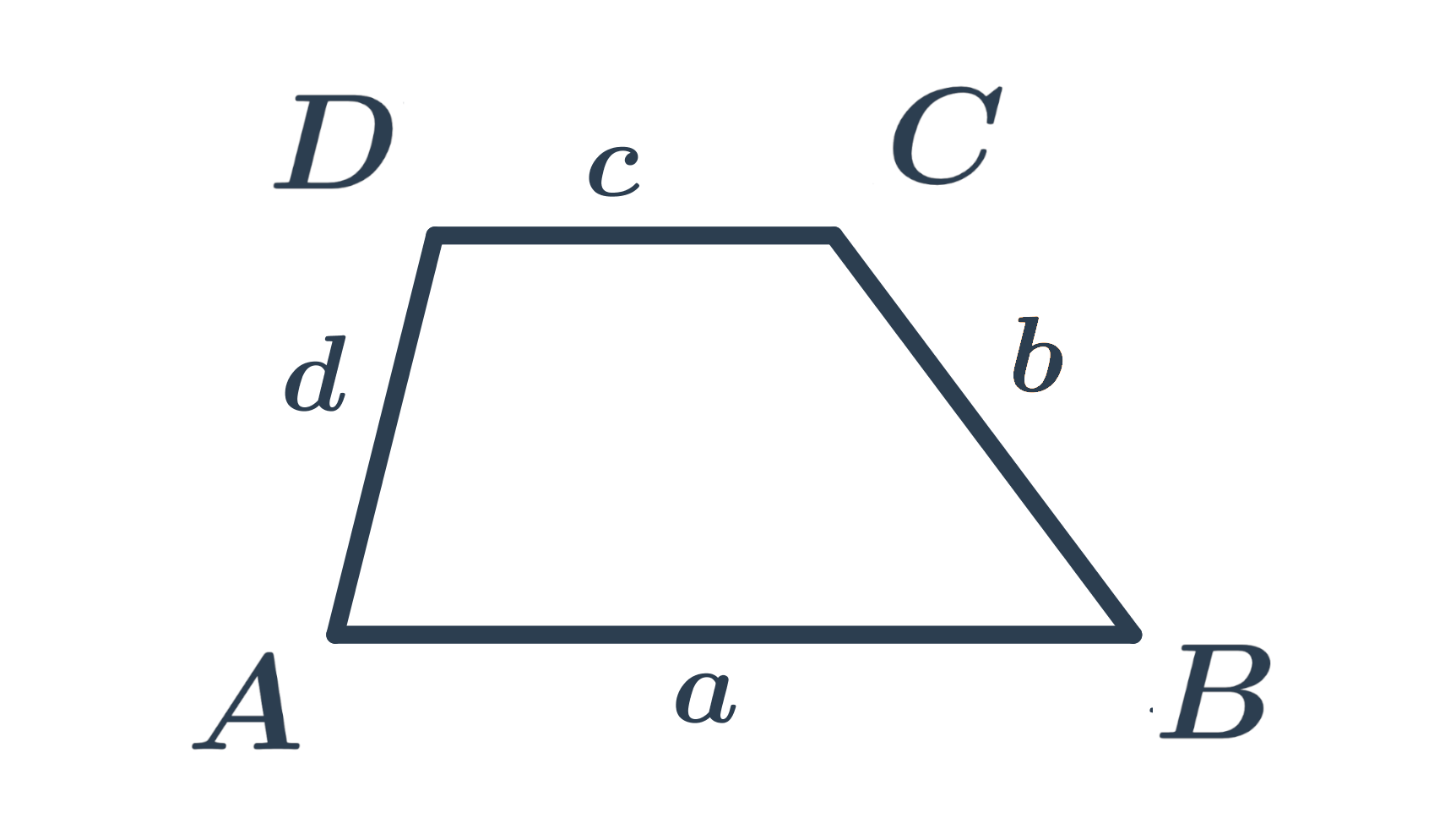
Pravouhlý lichobežník má dva z vnútorných uhlov pravé (základne lichobežníka sú rovnobežné, ak je jeden vnútorný uhol pravý, musí byť jeho doplnok do 180^{\circ} pri druhej základni tiež pravý).
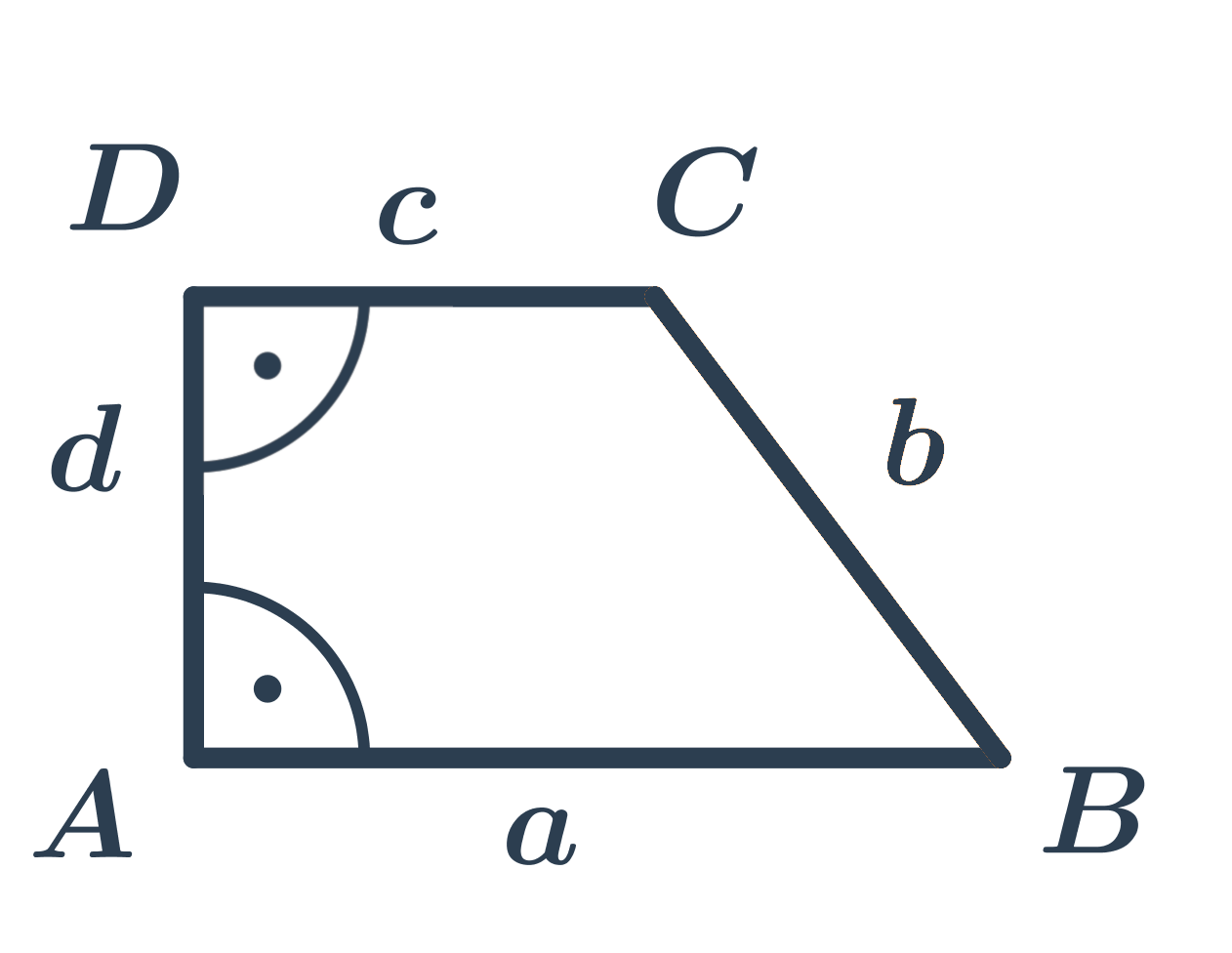
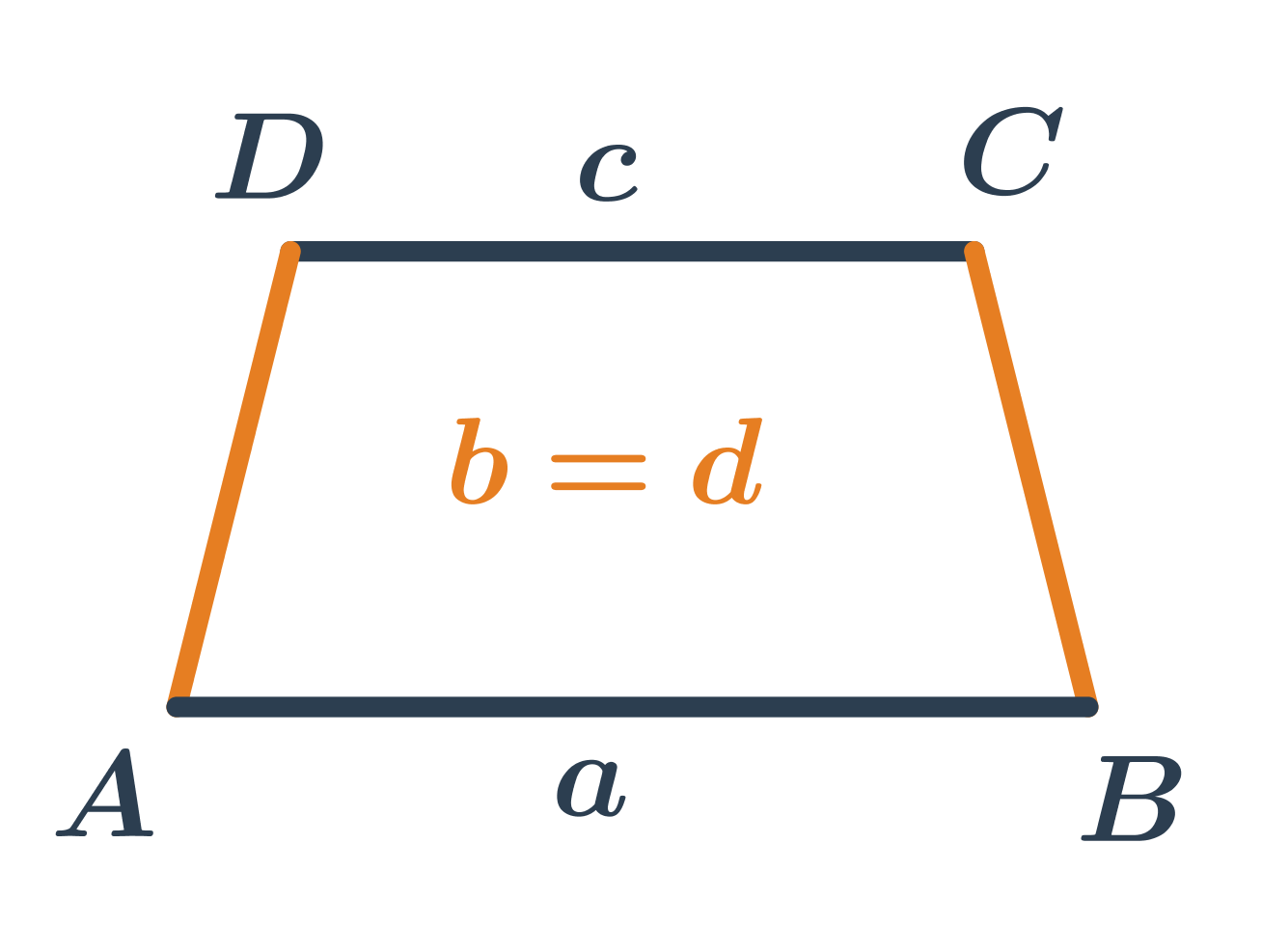
Rovnoramenný lichobežník má ramená rovnakej dĺžky.
Kruh a kružnica
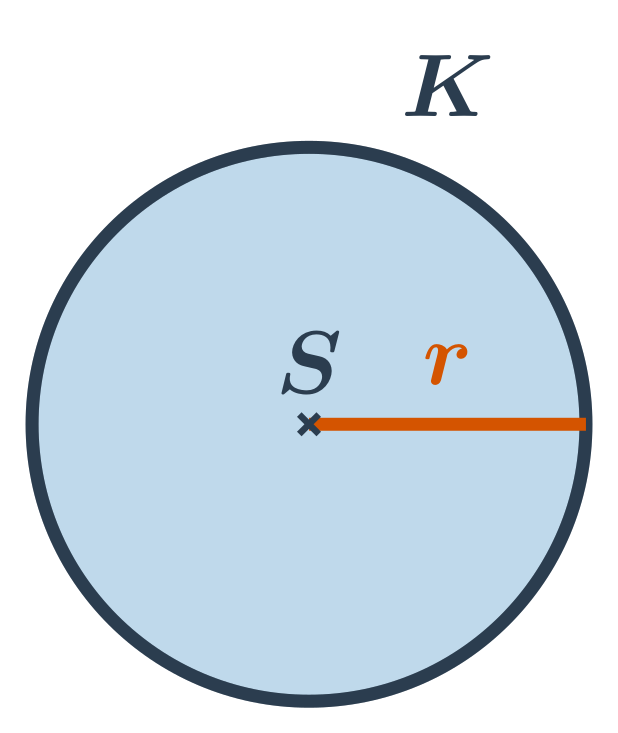
Kružnica s daným stredom S a polomerom r je tvorená všetkými bodmi v rovine, ktoré sú od stredu vzdialené presne o r. V prípade každého bodu v rovine potom môžeme určiť, kde ležia:
- na kružnici (ich vzdialenosť od S je rovná r)
- vo vnútornej oblasti kružnice (ich vzdialenosť od S je menšia než r, tieto body neležia na kružnici)
- vo vnútornej oblasti kružnice (ich vzdialenosť od S je väčšia než r, tieto body tiež neležia na kružnici)
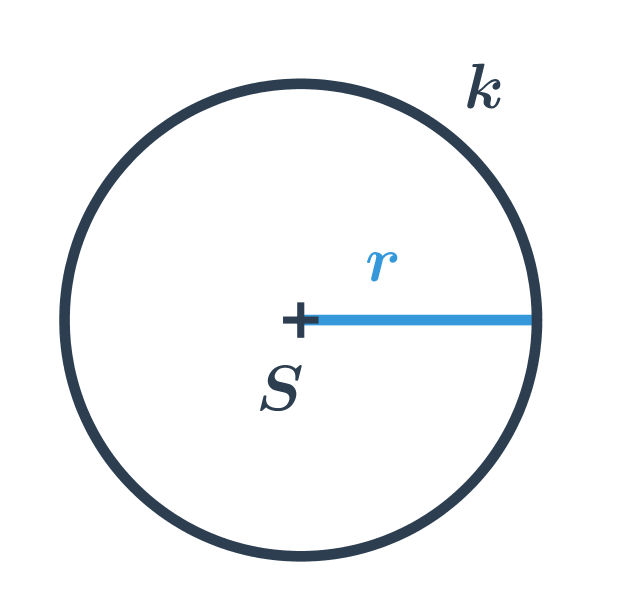
Kruh s daným stredom S a polomerom r je tvorený všetkými bodmi v rovine, ktoré sú od stredu vzdialené najviac o r. Kruh s daným stredom a polomerom je teda zjednotenie kružnice s rovnakým stredom a polomerom a jej vnútornou oblasťou. Stred S kruhu je bod, ktorý patrí do kruhu. (Zatiaľ čo stred kružnice neleží na kružnici, ale v jej vnútornej oblasti.)
Kocka, kváder
Kocka a kváder sú priestorové geometrické útvary, ktoré patria medzi mnohosteny, špeciálnejšie ide o zvláštne prípady hranolov.
Kocka je priestorový útvar, ktorý má šesť stien, tvar každej steny je štvorec. Všetky hrany kocky majú rovnakú dĺžku a všetky vnútorné uhly sú pravé, teda ich veľkosť je 90°. Príklady kocky v bežnom živote zahŕňajú kocky cukru alebo Rubikovu kocku.
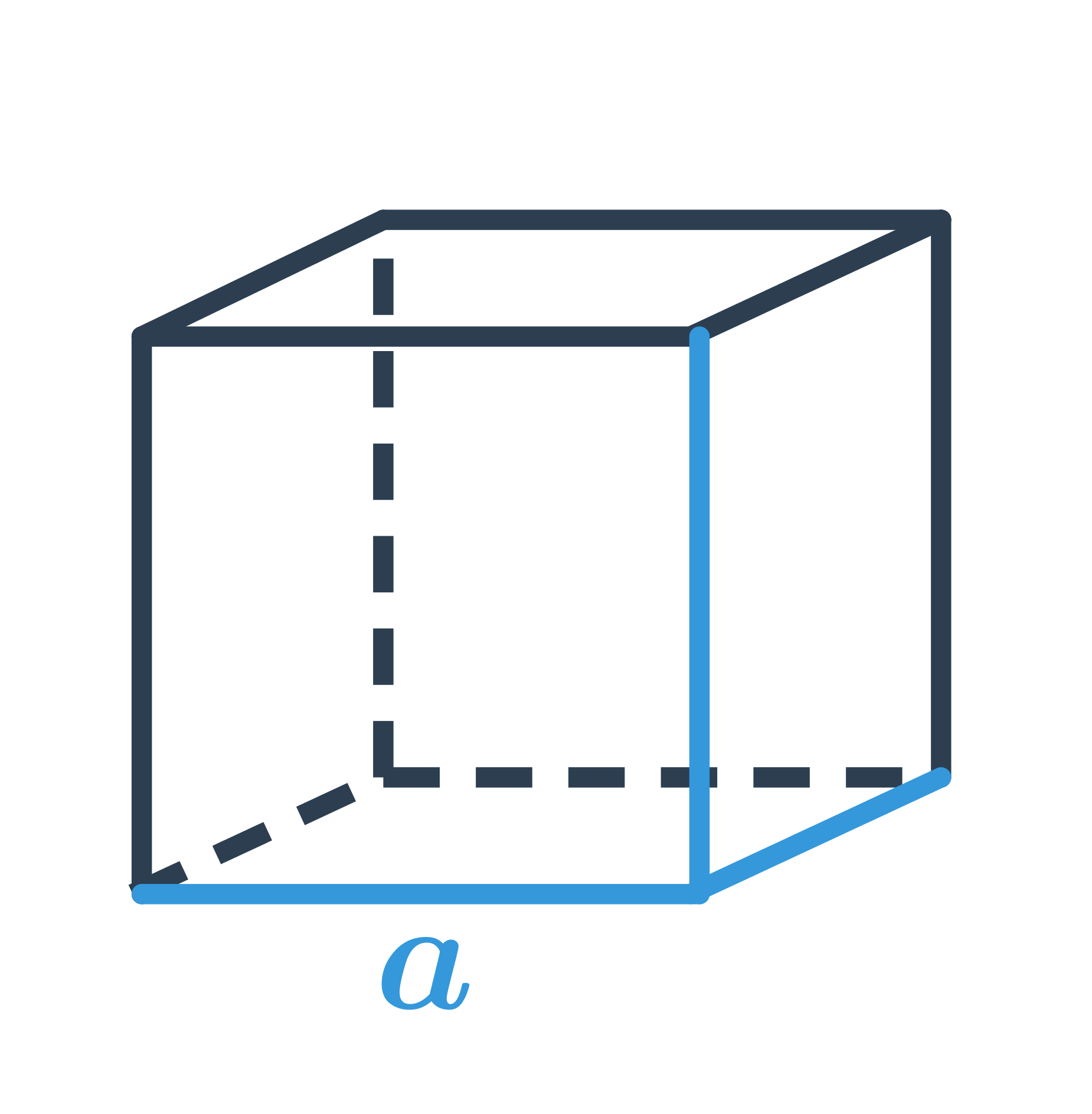
Na výpočet objemu kocky použijeme vzorec V = a^3, kde a je dĺžka hrany kocky.
Povrch kocky s dĺžkou hrany a sa vypočíta pomocou vzorca S = 6a^2.
Kváder je tiež hranol, ale na rozdiel od kocky majú jeho steny tvar obdĺžnikov. Kváder má tri rozmery: šírku, dĺžku a výšku, ktoré nemusia byť rovnaké, ako je tomu v prípade kocky. Kváder má šesť stien, tvar každej steny je obdĺžnik alebo štvorec, ak sú všetky steny tvaru štvorca, ide o kocku.
Príklady kvádrov v bežnom živote zahŕňajú krabice, knihy alebo tehly.
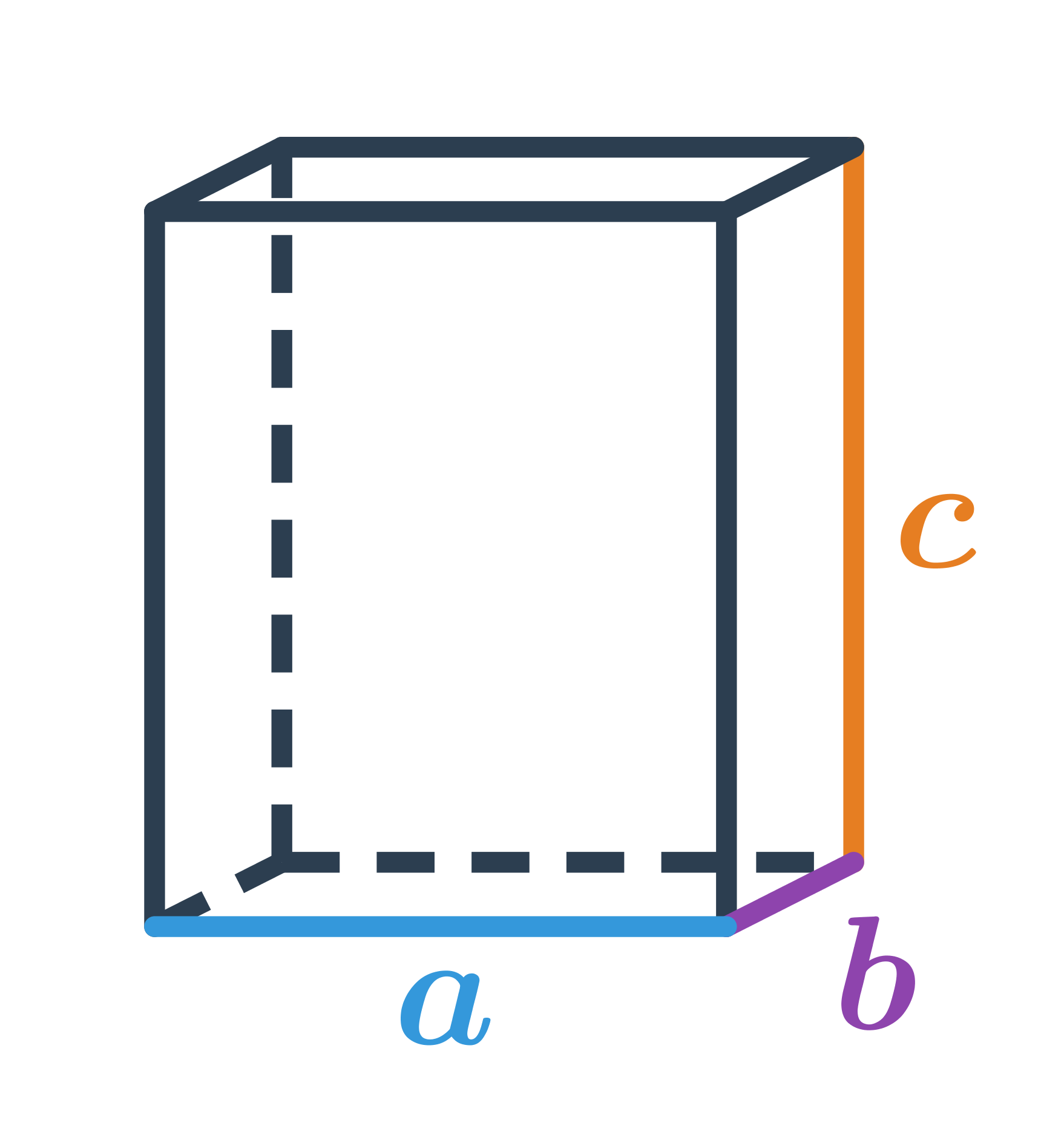
Objem kvádra získame vzorcom V = a \cdot b \cdot c, kde a,b,c sú rozmery kvádra.
Povrch kvádra vypočítame ako súčet obsahov všetkých jeho šiestich obdĺžnikových stien S = 2(ab + bc + ac). Dvojice protiľahlých stien sú zhodné obdĺžniky, preto majú rovnaké obsahy.
Hranol je priestorový geometrický útvar, ktorý má dve zhodné podstavy umiestnené v rôznych rovinách. Budeme sa zaoberať kolmými hranolmi, v ktorých sú zodpovedajúce strany podstavy vždy spojené bočnou stenou tvaru obdĺžnika alebo štvorca. (Pre kosé hranoly sú bočné steny rovnobežníky.) Podstavy hranola môžu mať rozličné tvary, napríklad môžu byť trojuholníkové, štvorcové, obdĺžnikové alebo aj mnohouholníkové.
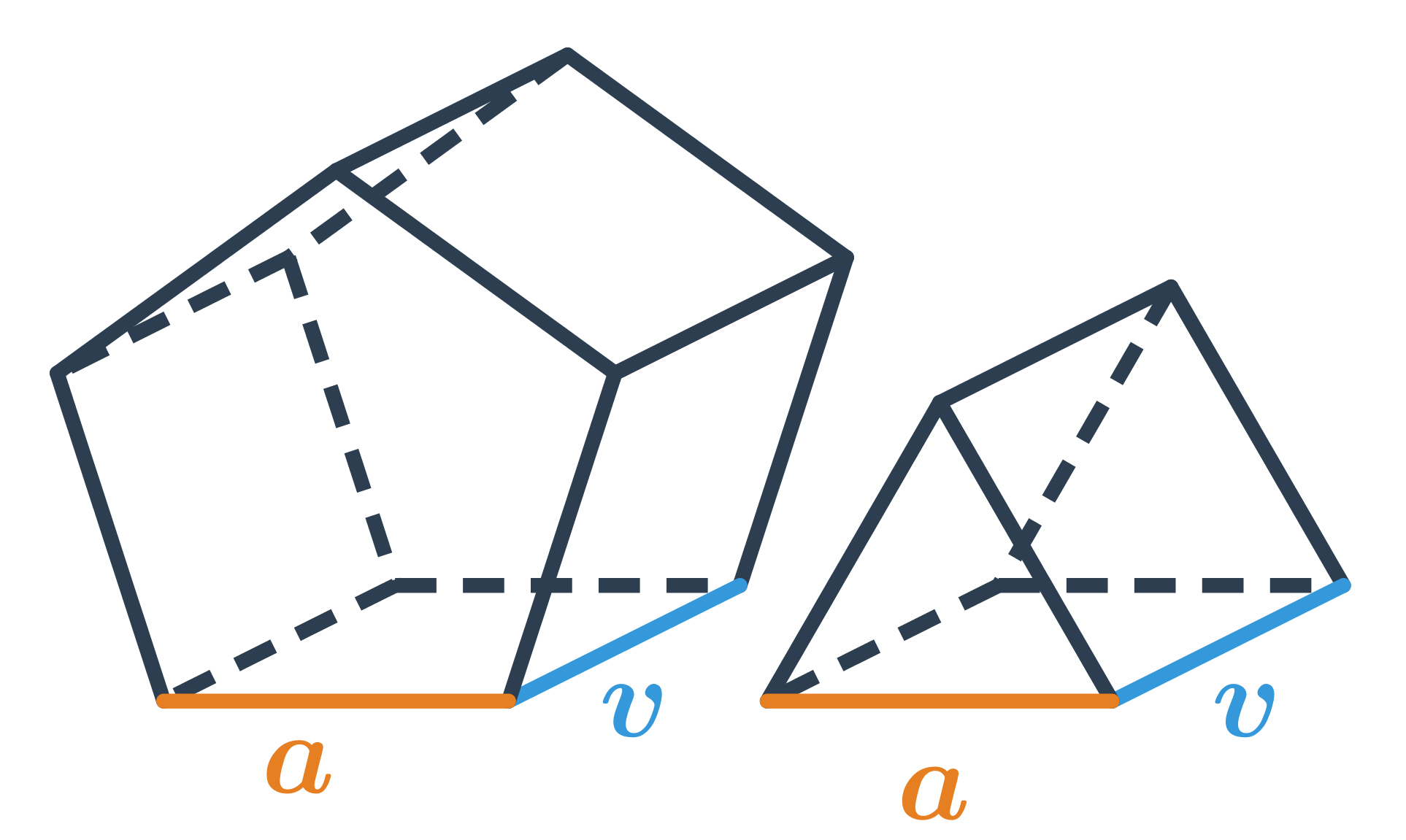
Vzorčeky pre objem a povrch hranola
Pre výpočet objemu hranola používame vzorec V = S_p \cdot v, kde S_p je obsah jednej podstavy a v je výška hranola.
Sieť hranola sa skladá z dvoch podstáv a plášťa, preto jeho povrch vypočítame ako súčet obsahov podstáv a obsahu plášťa: S = 2S_p + S_{pl}, kde S_{pl} je obsah plášťa, čo je súčet obsahov všetkých obdĺžnikových alebo štvorcových stien tvoriacich plášť.
Príklady hranolov
Pravidelný n-boký hranol má ako podstavy dva pravidelné n-uholníky.
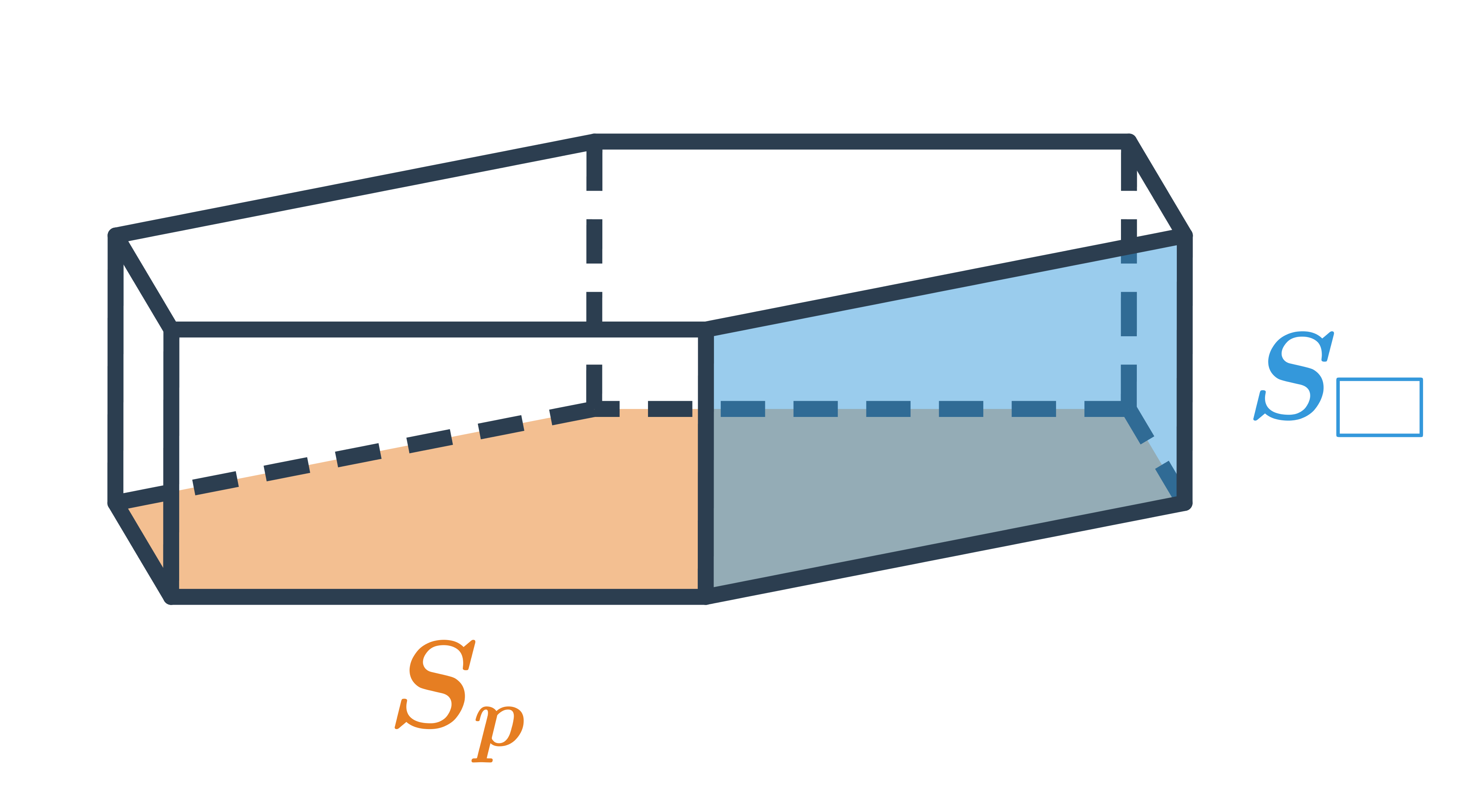
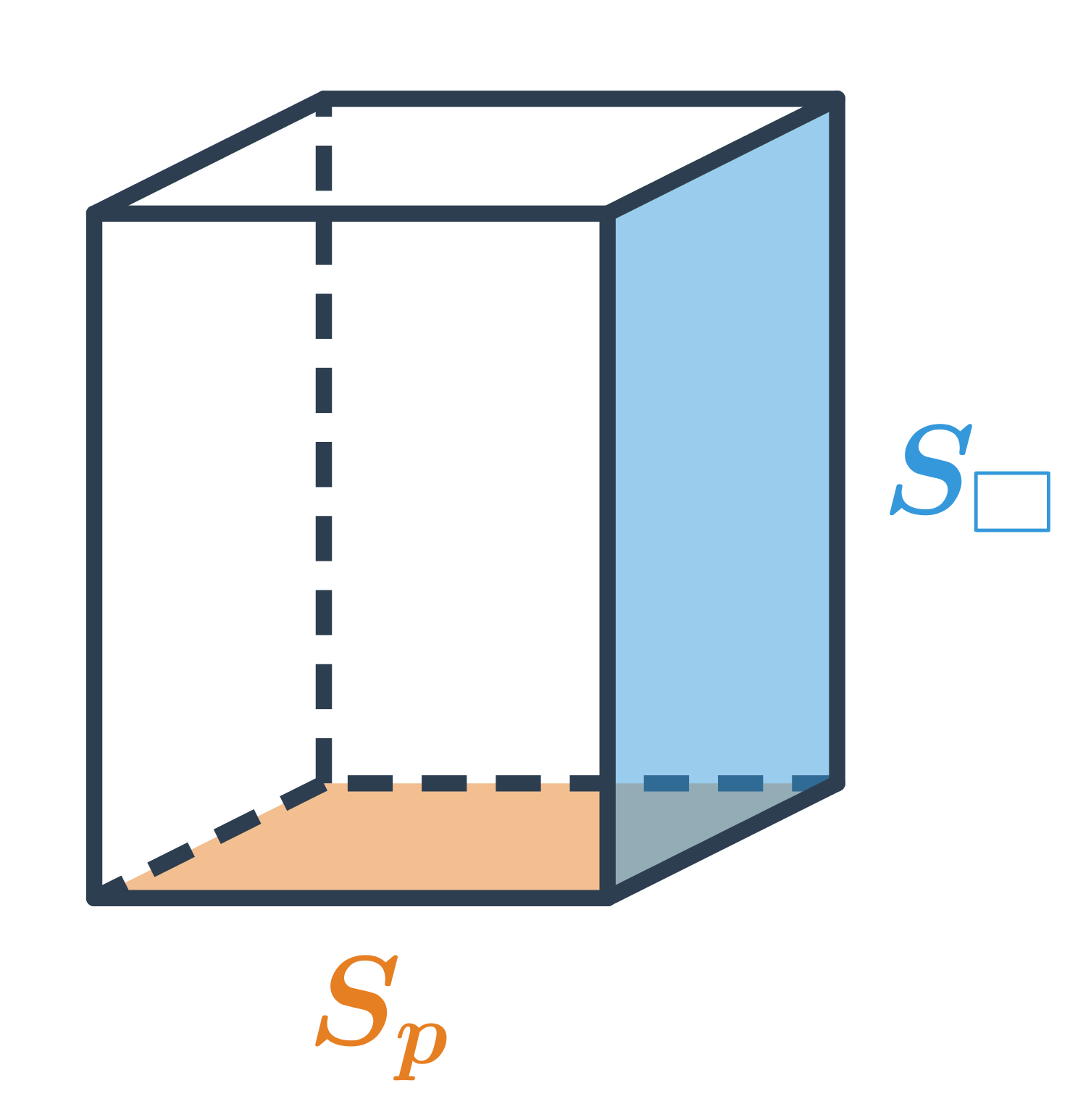
Špeciálne prípady štvorbokých hranolov sú kváder a kocka. Kváder môže a nemusí byť pravidelný štvorboký hranol. Kocka je pravidelný štvorboký hranol, ktorý navyše spĺňa a=v.
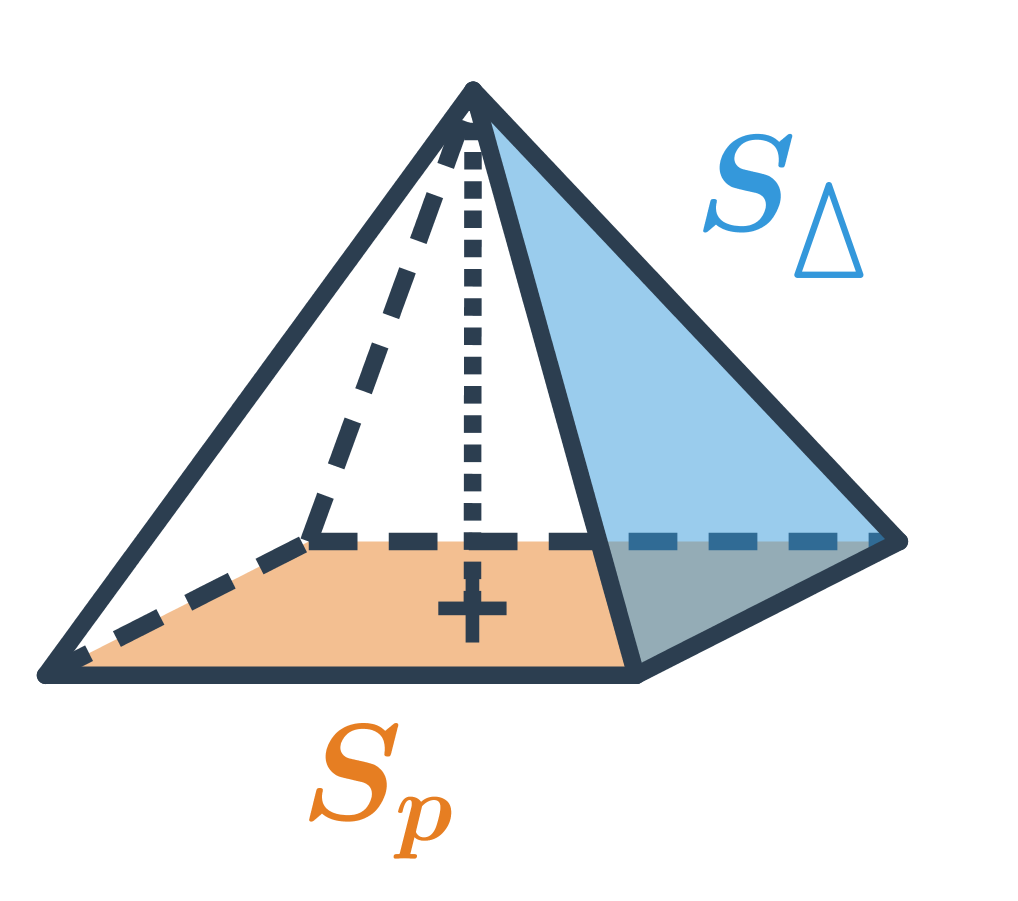
Ihlan je priestorový geometrický útvar, ktorý má jednu podstavu a plášť tvorený trojuholníkmi. Podstava ihlanu môže byť ľubovoľný mnohouholník (napríklad štvorec, obdĺžnik alebo trojuholník) a všetky bočné steny (plášť) sa stretávajú v jednom spoločnom bode nazývanom vrchol ihlanu. Príkladom ihlanov sú pyramídy zo starovekého Egypta, vypadajú zhruba ako ihlany so štvorcovou podstavou a štyrmi trojuholníkovými bočnými stenami.
Vzorce pre objem a povrch
Objem ihlanu V = \frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy a v je výška ihlanu, čo je vzdialenosť vrcholu od roviny podstavy. (Veľkosť výšky ihlanu získame ako dĺžku úsečky, ktorá vedie od vrcholu k rovine podstavy a je kolmá na túto rovinu.)
Povrch ihlanu získame ako súčet obsahu podstavy a obsahu plášťa S_p (obsah plášťa je rovný súčtu obsahov všetkých bočných trojuholníkových stien ihlanu). Celkovo je povrch ihlanu S = S_p + S_{pl}, v prípade pravidelného šesťbokého ihlanu na obrázku je: S=Sp + 6 \cdot S_{\Delta}
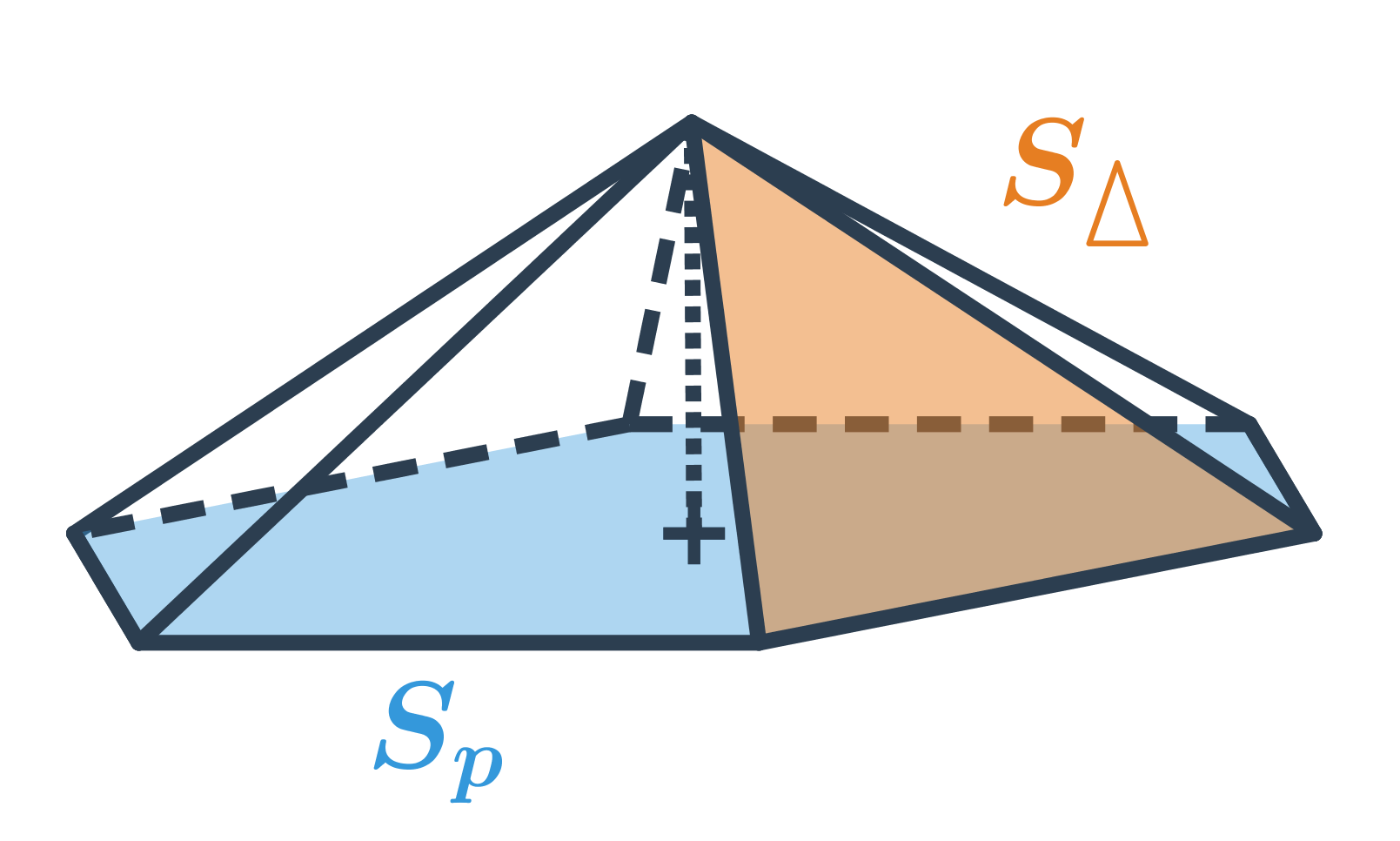
Niektoré ihlany majú pravidelnú podstavu, vrchol umiestnený priamo nad stredom podstavy a všetky trojuholníkové steny z plášťa rovnaké, ale všeobecne sa môže výpočet obsahu každej z týchto trojuholníkových stien líšiť v závislosti od tvaru podstavy ihlanu.
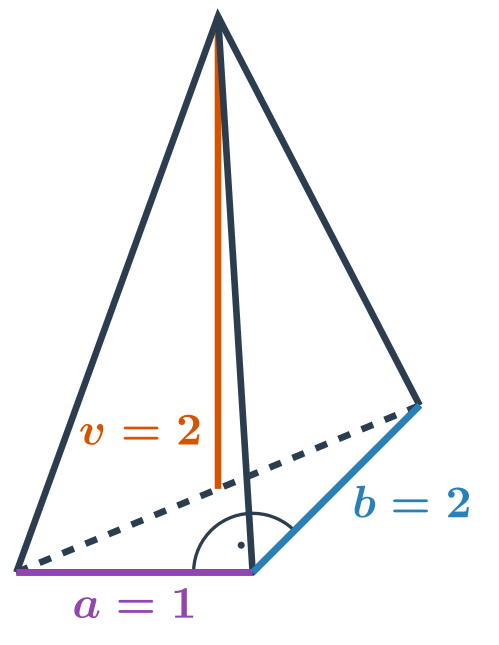
Špeciálne prípady
Pravidelný štvorsten je ihlan, ktorého základňa aj všetky tri bočné steny sú rovnostranné trojuholníky. Je jedným z Platónskych telies.
Ak máme pravidelný štvorsten, ktorého steny sú rovnostranné trojuholníky s dĺžkou každej strany a, vieme si pomocou Pytagorovej vety vypočítať výšku každého z týchto rovnostranných trojuholníkov \frac{\sqrt{3}}{2} a.
Povrch pravidelného štvorstenu
- Obsah podstavy pravidelného štvorstenu so stranou s dĺžkou a je obsah jedného zo štyroch rovnakých rovnostranných trojuholníkov: S_p = \frac{1}{2} \cdot a \cdot \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{4} a^2.
- Povrch pravidelného štvorstenu so stranou dĺžky a je: 4 \cdot S_p = \sqrt{3} \cdot a^2
Objem pravidelného štvorstenu
- V rovnostrannom trojuholníku leží ťažnica na výškach a zároveň na osách vnútorných uhlov. Vrchol pravidelného štvorstenu leží na priamke, ktorá je kolmá k jeho podstave a pretína ju v ortocentre (čo je zároveň tiež ťažisko rovnostranného trojuholníka).
- Môžeme teda pomocou Pytagorovej vety vypočítať nie len výšku trojuholníkov, ktoré tvoria steny pravidelného štvorstenu, ale tiež výšku celého telesa:
- v^2 = a^2 - (\frac{2}{3} \cdot \frac{\sqrt{3}}{2} a )^2 = (1-\frac{1}{\sqrt{3}})\cdot a^2
- v = \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a
- Objem pravidelného štvorstenu so stranou s dĺžkou a je:
- \frac{1}{3} S_p \cdot v = \frac{1}{3}\cdot \frac{\sqrt{3}}{4} a^2 \cdot \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a = \frac{1}{4\cdot \sqrt{3}}\cdot \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a^3
Pravidelný n-boký ihlan má ako podstavu pravidelný n-uholník, jeho plášť tvorí n rovnoramenných trojuholníkov. Napríklad podstava pravidelného štvorbokého ihlanu je štvorec, jeho plášť tvoria štyri rovnoramenné trojuholníky.
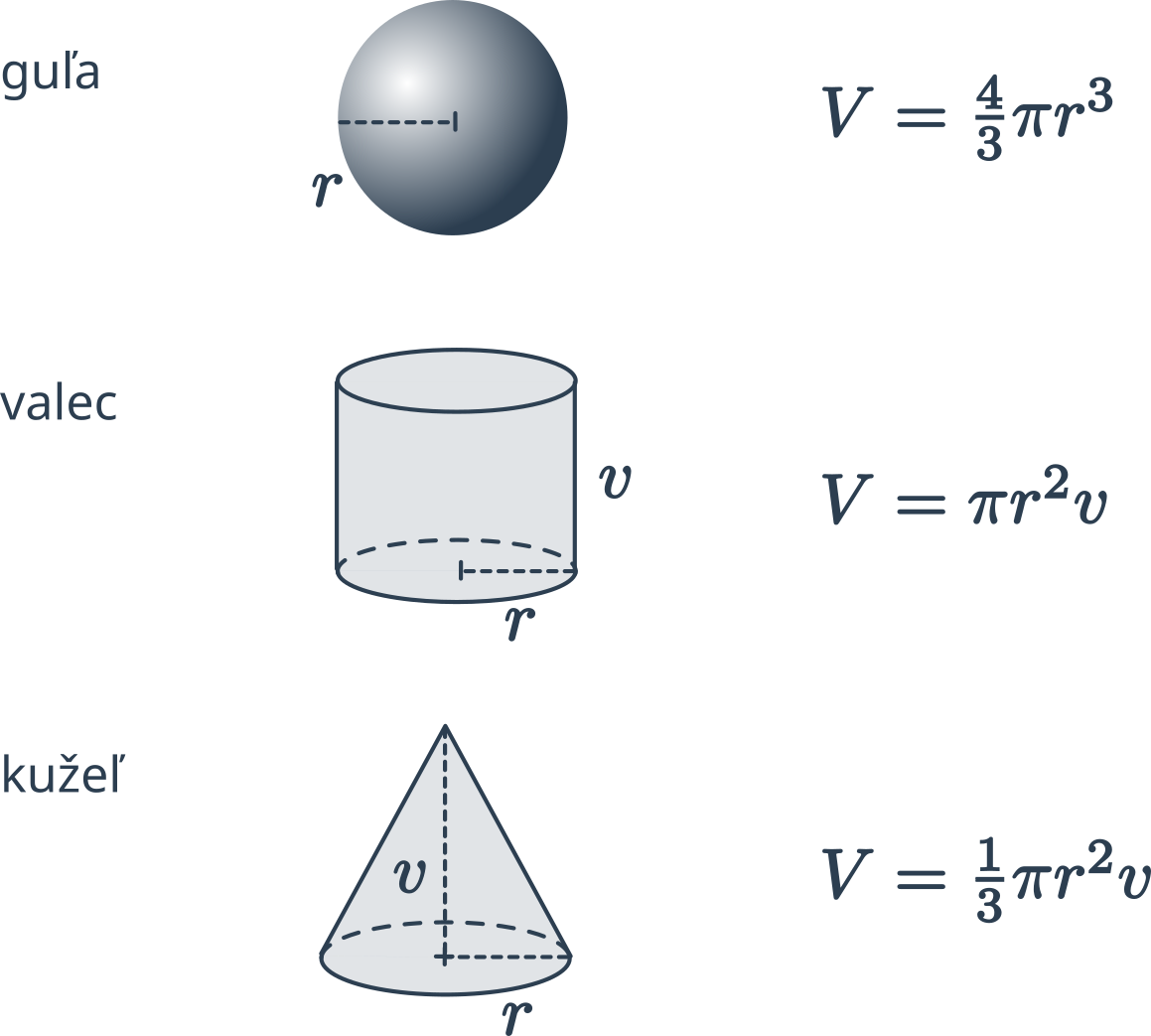
Guľa je priestorový geometrický útvar, ktorý má tvar dokonale guľatého telesa. Všetky body na povrchu gule sú rovnako ďaleko od stredu, táto vzdialenosť sa nazýva polomer gule. Guľa je symetrická vo všetkých smeroch, čo znamená, že nezáleží na tom, ako ju otočíme, jej tvar zostane rovnaký.
Príklady gule v bežnom živote zahŕňajú basketbalovú loptu, zemeguľu alebo guľôčku z ložiska.
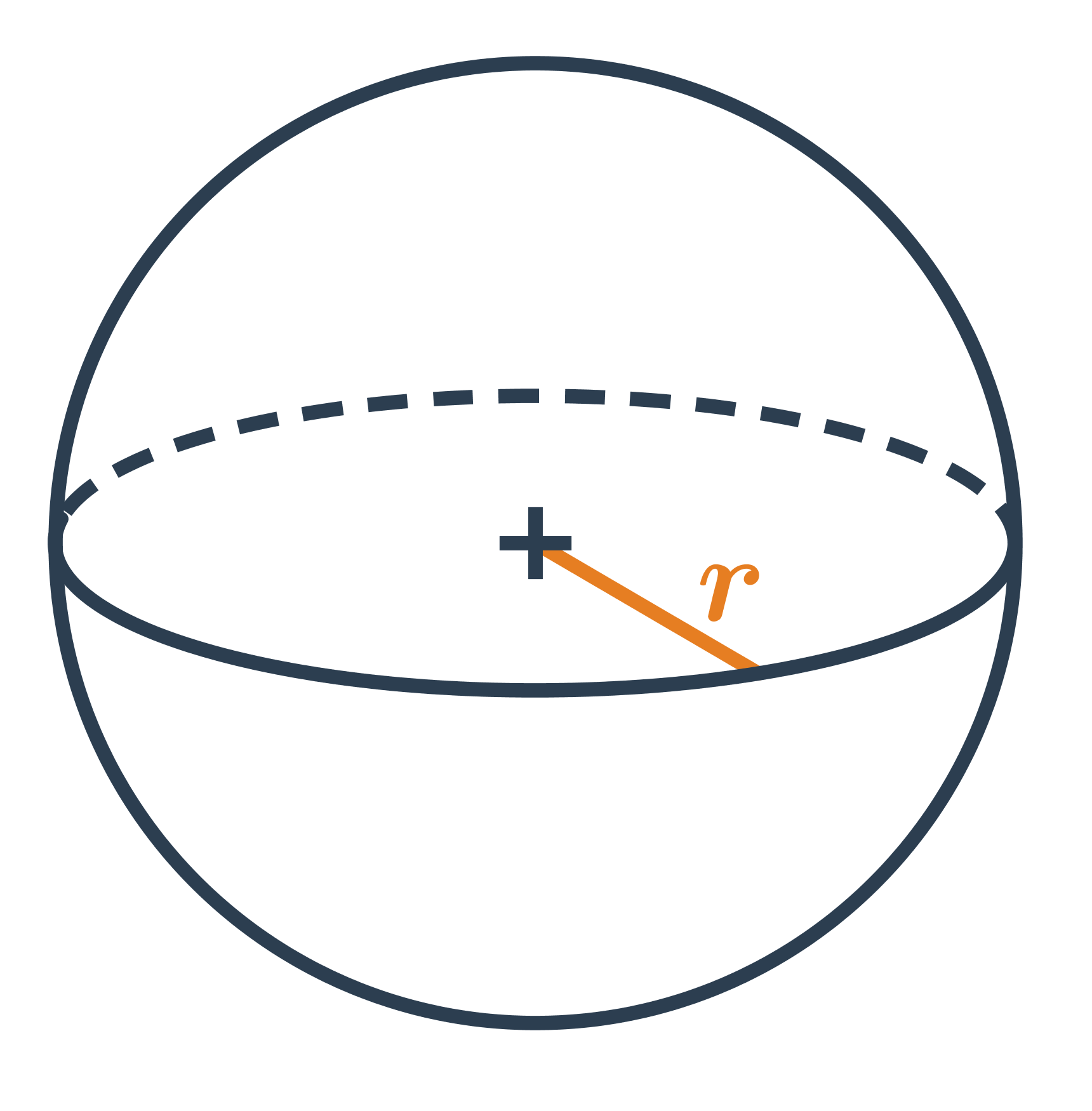
Na výpočet objemu gule používame vzorec V = \frac{4}{3} \pi r^3, kde r je polomer gule.
Povrch gule sa vypočíta pomocou vzorca S = 4 \pi r^2, kde zase r značí polomer gule.
Guľa nemá rohy ani hrany, čo ju odlišuje od mnohých iných geometrických útvarov. Táto jedinečná vlastnosť dáva guli významnú rolu v rôznych oblastiach, vrátane fyziky, kde sa používa napríklad na modelovanie ideálnych telies v teórii gravitácie. Predmetom štúdia v neeuklidovskej geometrii môžu zase byť útvary, ktoré nie sú časťou roviny, ale guľovej plochy (potom ide o sférickú geometriu, teda geometriu na sfére).
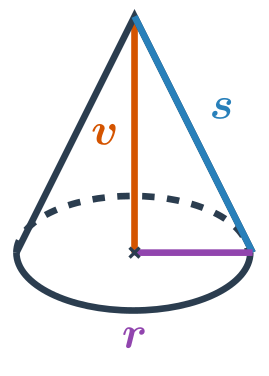
Kužeľ je priestorový geometrický útvar s kruhovou podstavou. Zužuje sa smerom k jednému bodu zvanému vrchol. Ide o útvar, ktorý vznikne, keď sa okolo svojej osi otáča rovnoramenný trojuholník. Príkladom kužeľa v bežnom živote je kornút zmrzliny alebo dopravný kužeľ.
Vzorce pre objem a povrch
Objem kužeľa je možné vypočítať pomocou vzorca: V = \frac{1}{3} \pi \cdot r^2 \cdot v, kde r je polomer podstavy a v je výška kužeľa, čo je vzdialenosť vrcholu od roviny, v ktorej leží podstava kužeľa.
Povrch kužeľa získame sčítaním obsahu základne a obsahu plášťa S = \pi \cdot r^2 + \pi \cdot r s, kde s je tzv. strana kužeľa, čo je dĺžka úsečky spájajúca vrchol kužeľa s okrajom jeho základne.
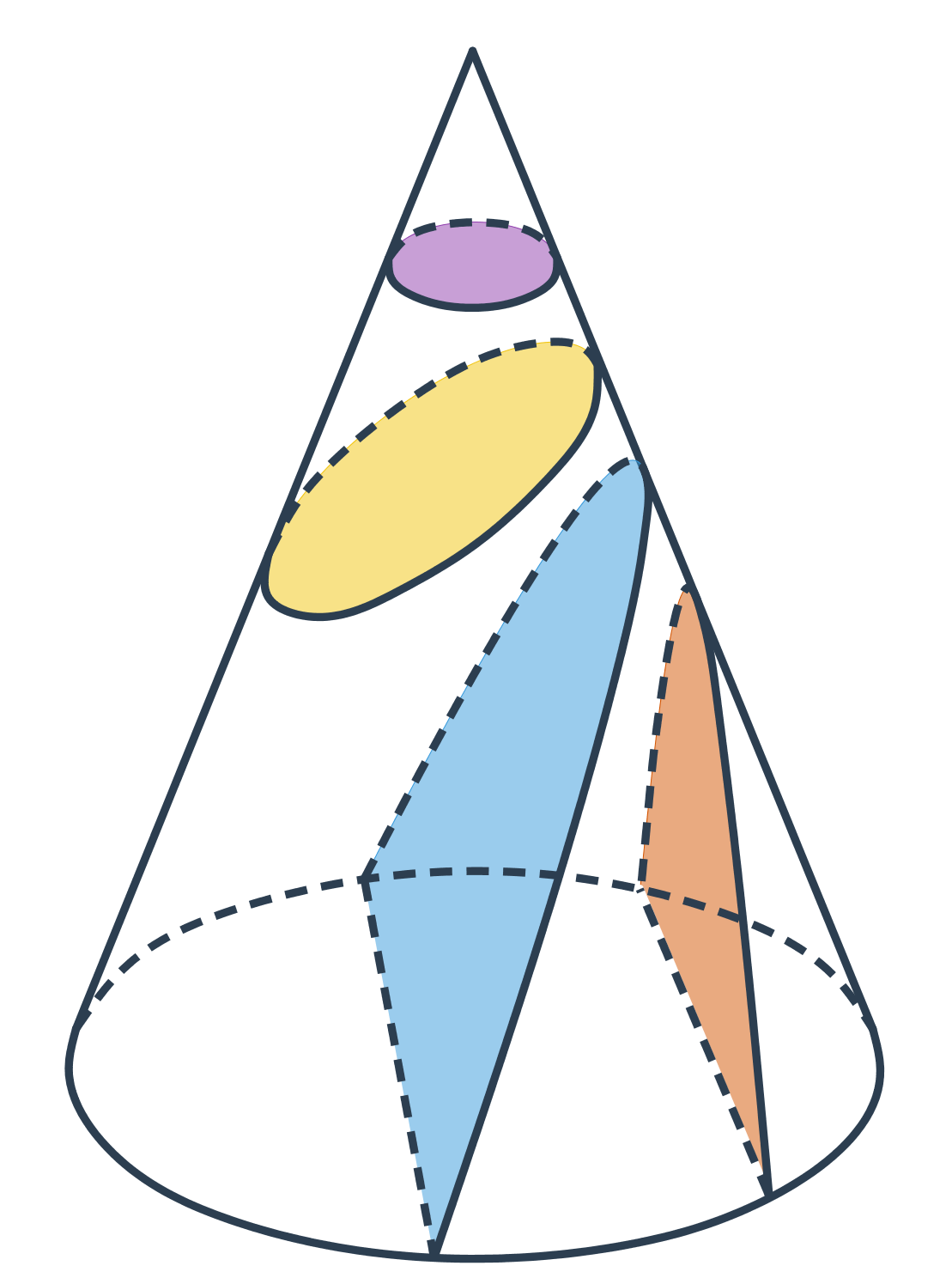
Kužeľosečky
Krivky, ktoré vznikajú prienikom kužeľového povrchu s rovinou sa nazývajú kužeľosečky. Patria medzi ne napríklad kružnica, elipsa, parabola a hyperbola.
Obsah a obvod
Obsah značíme S. Obsah vyjadruje, koľko „miesta v rovine“ útvar zaberá. Meria sa v jednotkách obsahu.
Obvod značíme o. Obvod je súčet dĺžok čiar, ktoré útvar vymedzujú. Obvod sa meria v jednotkách dĺžky.
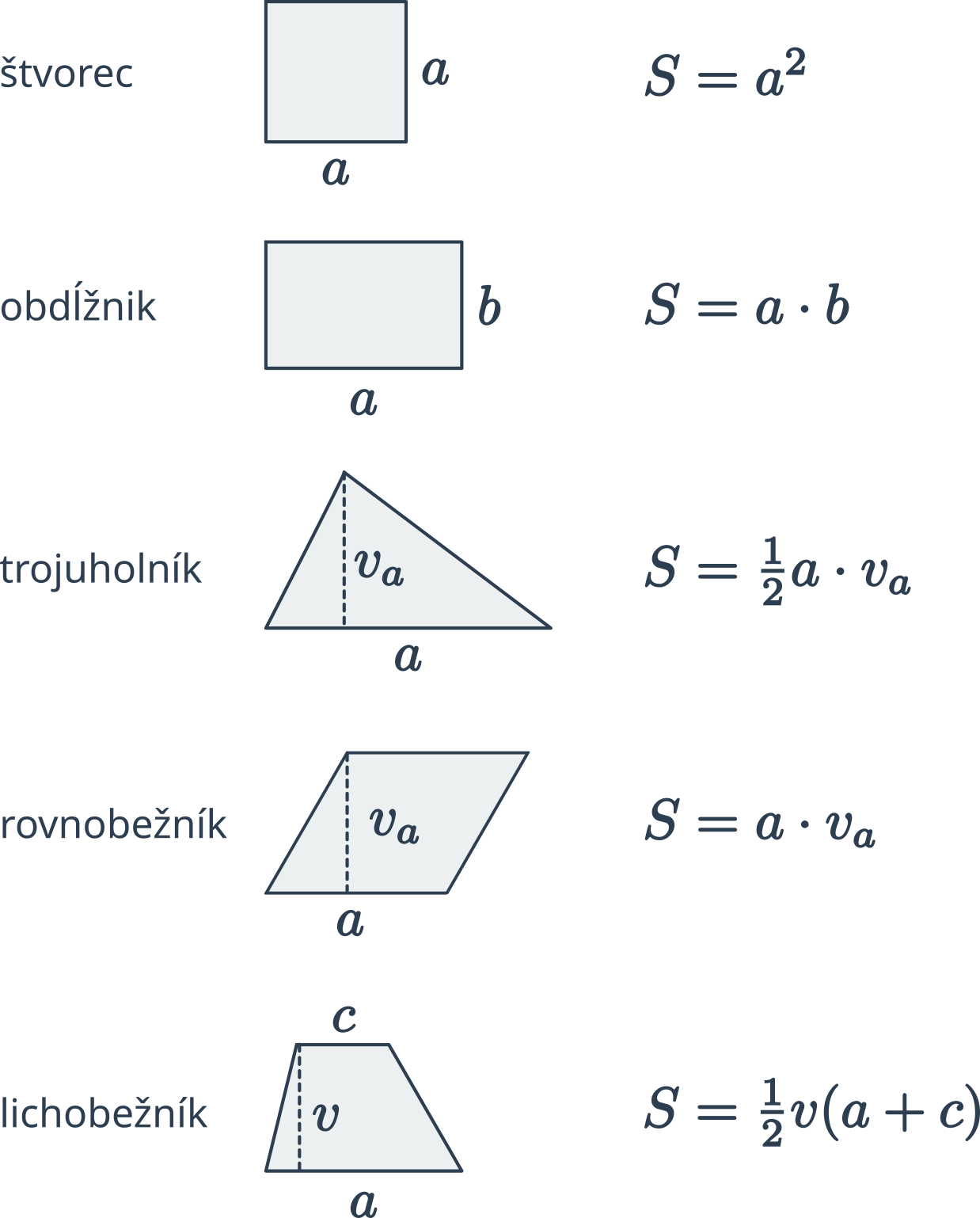
Prehľad vzorcov pre obsah a obvod základných geometrických útvarov:
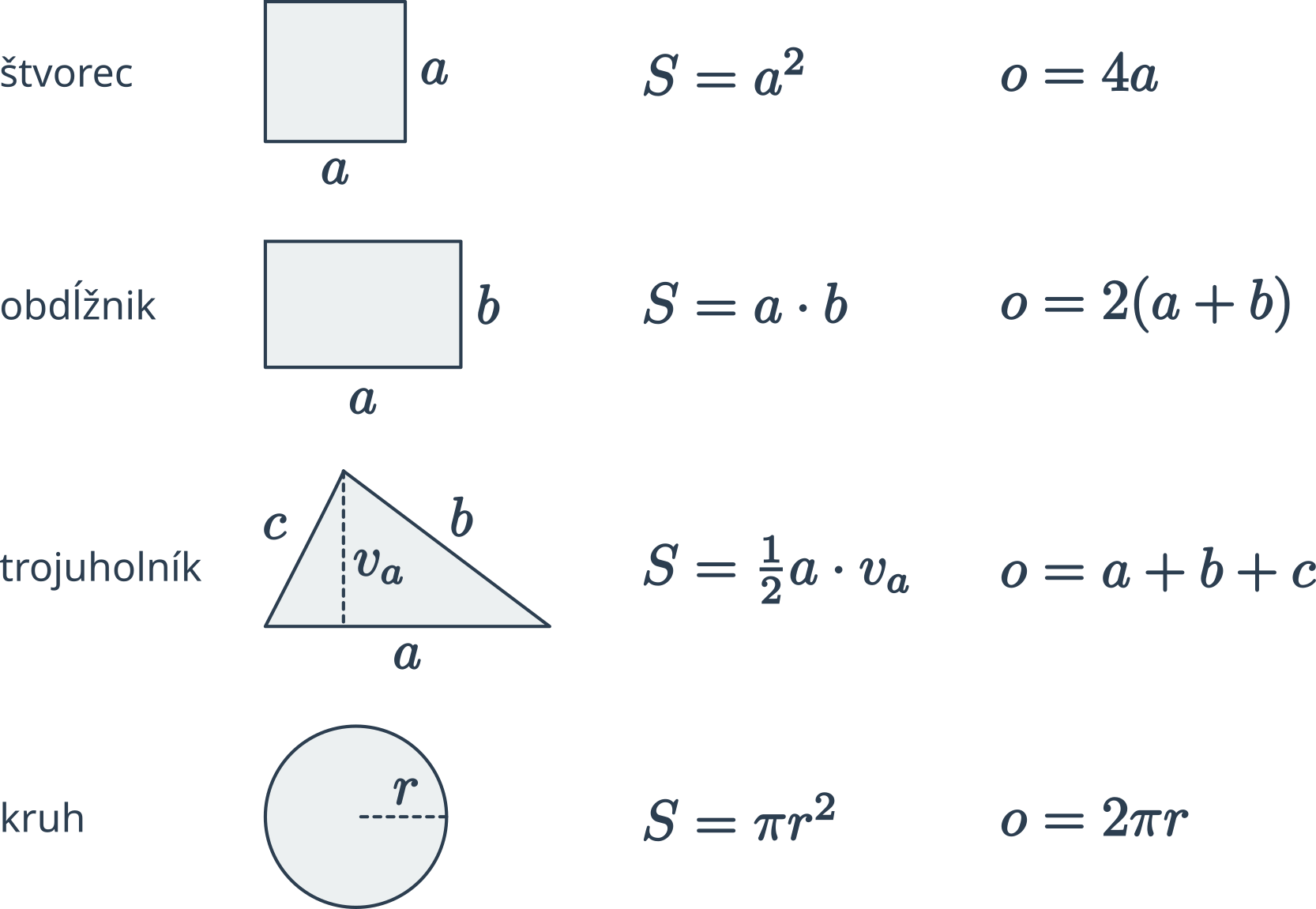
Dĺžka oblúka
Dĺžka oblúka
Dĺžku oblúka, ktorý na kružnici s polomerom r zodpovedá stredovému uhlu \alpha vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Príklady
- Dĺžka oblúka na obrázku je: \frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
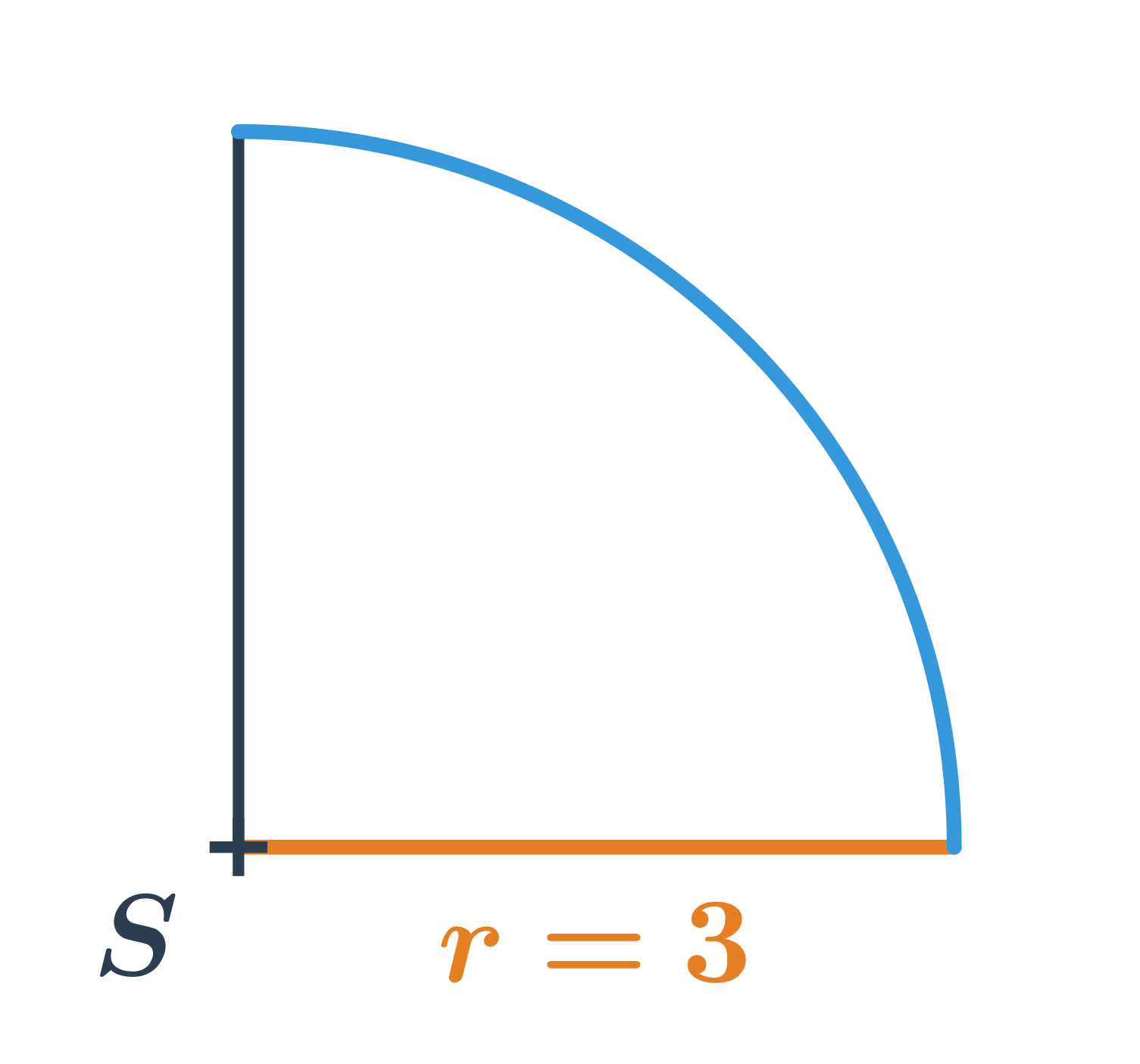
- Dĺžka celej kružnice (teda pre celých 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r
Obvod: mix
Obvod trojuholníkov a štvoruholníkov je jednoducho súčet dĺžok ich strán.
| Útvar | Vlastnosti | Obvod |
|---|---|---|
| trojuholník | strany a, b, c | o = a + b + c |
| štvorec | strana a | o = 4a |
| obdĺžnik | strany a, b | o = 2(a+b) |
| rovnobežník | strany a, b | o = 2(a+b) |
| všeobecný štvoruholník | strany a, b, c, d | o = a+b+c+d |
Obsah kruhu
Vzorce
Obvod kruhu (aj kružnice) s polomerom r je o=2\pi r. Pre priemer d platí o = \pi d.
Obsah kruhu s polomerom r je S=\pi r^2. Pre priemer d platí S = \frac{1}{4} \pi d^2.
Konštanta \pi sa nazýva tiež Ludolfovo číslo. \pi je iracionálne číslo, čo znamená, že ho nie je možné vyjadriť zlomkom ani zapísať presne v desiatkovej sústave. Približná hodnota \pi je 3,14159265.
Pri výpočte obsahu a obvodu kruhu dávame dobrý pozor na to, či vychádzame zo znalosti polomeru alebo priemeru. Zámena priemeru za polomer je častou chybou.
Intuícia
Základnú intuíciu za vzorcami na výpočet obsahu a obvodu kruhu približuje nižšie uvedený obrázok. Žlté štvorce majú obsah r^2. Oranžový štvorec sa skladá zo štyroch žltých štvorcov, takže má obsah 4\cdot r^2. Kruh má „o trochu menší“ obsah než oranžový štvorec, čo zodpovedá tomu, že obsah kruhu je približne 3{,}14 \cdot r^2. Obvod oranžového štvorca je 8\cdot r. Obvod kruhu je zase „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Príklady
- Majme kruh s polomerom 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm. Jeho obsah je \pi \cdot 3^2 \approx 3{,}14\cdot 9 \approx 28,3 cm².
- Kružnica s priemerom 2 cm má obvod \pi \cdot 2 \approx 6,3 cm. Jej vnútro má obsah \frac{1}{4} \pi \cdot 2^2 = \pi \approx 3,14 cm².
- Stredový kruh na futbalovom ihrisku má polomer 9{,}1 metru. Ak ho chceme obísť po jeho okrajovej čiare, prejdeme 2 \pi \cdot 9{,}1 \approx 57 metrov. Ak by sme chceli všetku trávu v kruhu nafarbiť na ružovo, museli by sme nafarbiť \pi \cdot 9{,}1^2 \approx 260 m² trávy.
Obsah kruhového výseku
Obsah kruhového výseku
Obsah kruhového výseku so stredovým uhlom \alpha a polomerom r vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2
Dĺžka oblúka
Podobne, dĺžku oblúka, ktorý na kružnici s polomerom r a zodpovedá stredovému uhlu \alpha vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Príklady
- Kruhový výsek na obrázku má obsah: \frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi
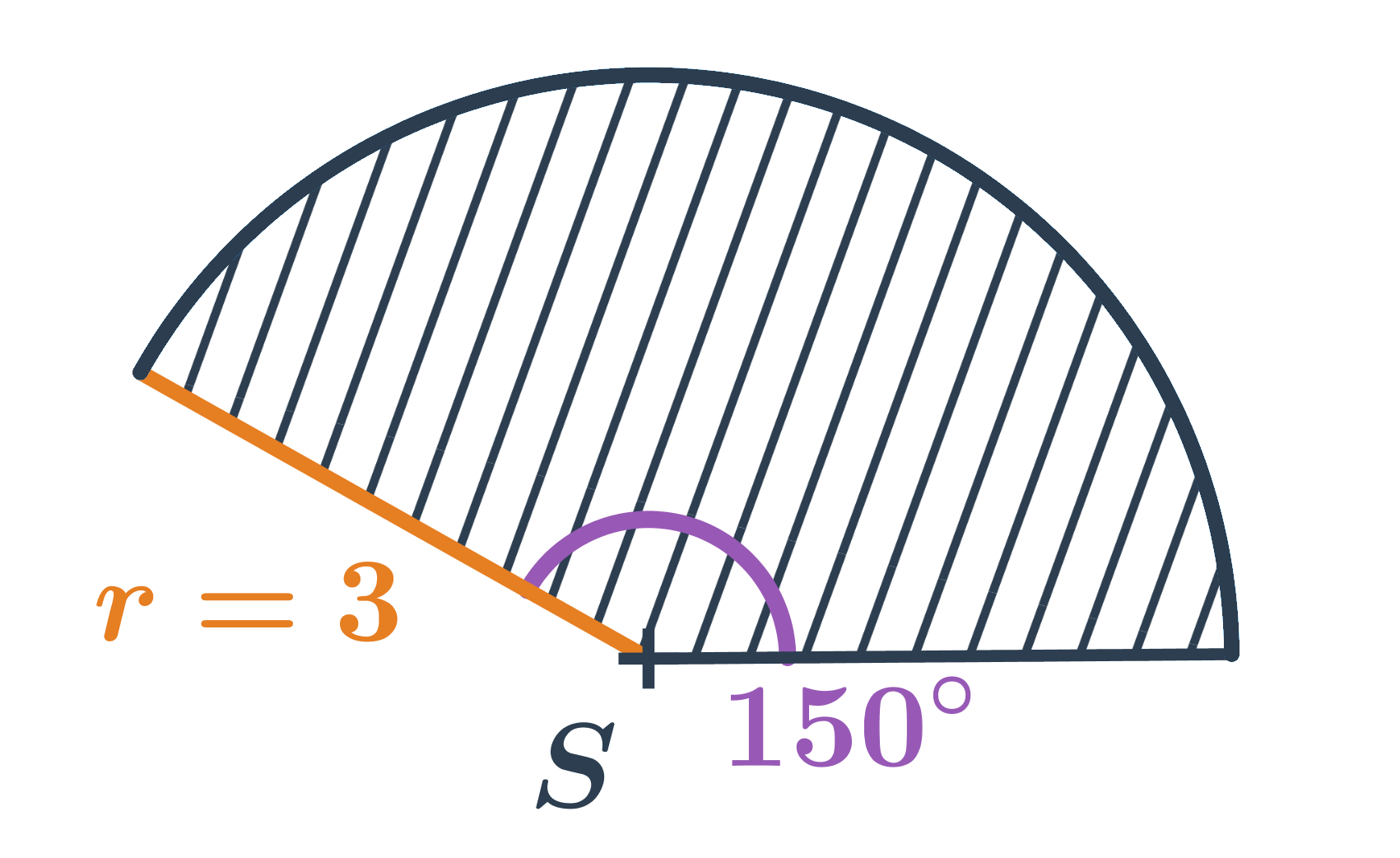
- Obsah celého kruhu (výseku so stredovým uhlom 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2
- Dĺžka oblúka na obrázku je: \frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
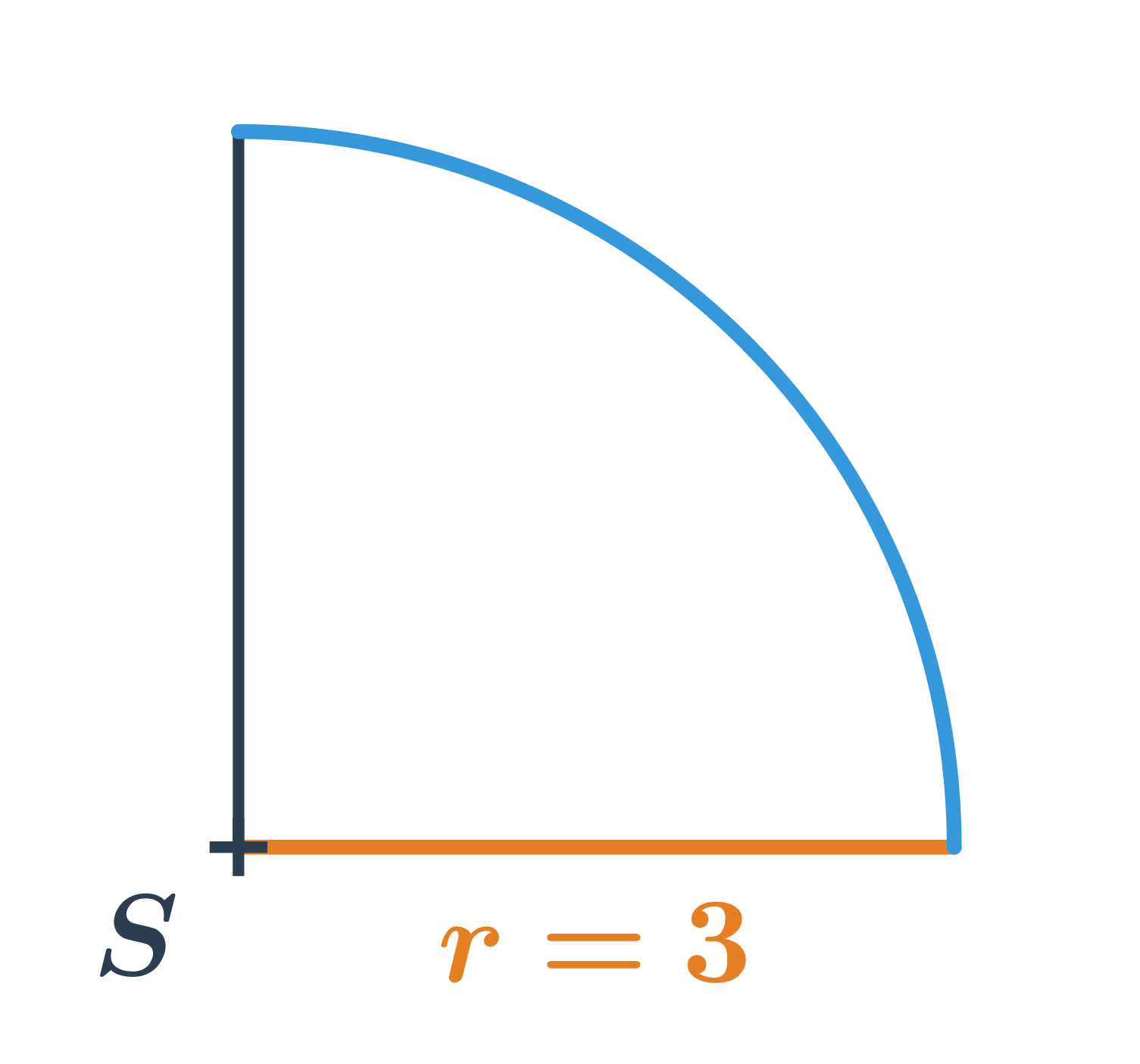
- Dĺžka celej kružnice (teda pre celých 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r
Obsah: mix
| Útvar | Vlastnosti | Obsah |
|---|---|---|
| trojuholník | strana a, príslušná výška v_a | S = \frac12 \cdot a\cdot v_a |
| štvorec | strana a | S = a^2 |
| obdĺžnik | strany a, b | S = a\cdot b |
| rovnobežník | strana a, príslušná výška v_a | S = a\cdot v_a |
| lichobežník | základne a, c, výška v | S = \frac12 \cdot (a+c) \cdot v |
Objem a povrch
Objem telesa vyjadruje, koľko miesta v priestore teleso zaberá. Môžeme si ho predstaviť ako množstvo vody, ktoré by sme potrebovali, keby sme chceli teleso „napustiť“. Na vyjadrenie objemu využívame jednotky objemu.
Povrch telesa je súčet obsahov všetkých plôch, ktoré teleso ohraničujú. Môžeme si ho predstaviť ako veľkosť farebného papiera, ktorý potrebujeme na „polepenie“ telesa. Na vyjadrenie povrchu využívame jednotky obsahu.
Značenie vo vzorcoch
| V | objem |
| S | povrch |
| S_p | obsah podstavy |
| S_{pl} | obsah plášťa |
| a, b, c | dĺžky strán |
| r | polomer |
| v | výška |
| s | strana kužeľa |
Vzorce
| Útvar | Objem | Povrch | |
|---|---|---|---|
| kocka | V = a^3 | S=6a^2 | |
| kváder | V = abc | S = 2(ab+ac+bc) | |
| guľa | V=\frac43\pi r^3 | S=4\pi r^2 | |
| valec | V=S_p\cdot v =\pi r^2 v | S=2S_p+S_{pl} =2\pi r(r+v) | |
| kužeľ | V=\frac{1}{3}S_p\cdot v =\frac13 \pi r^2 v | S =S_p+S_{pl} =\pi r(r+\sqrt{r^2+v^2})=\pi r^2 +\pi rs | |
| ihlan | V=\frac{1}{3}S_p\cdot v | S=S_p+S_{pl} | |
| pravidelný štvorboký ihlan | V=\frac{1}{3}S_p\cdot v=\frac{1}{3} a^2v | ||
| hranoľ | V= S_p\cdot v | S=2\cdot S_p+S_{pl} |
Povrch hranatých telies
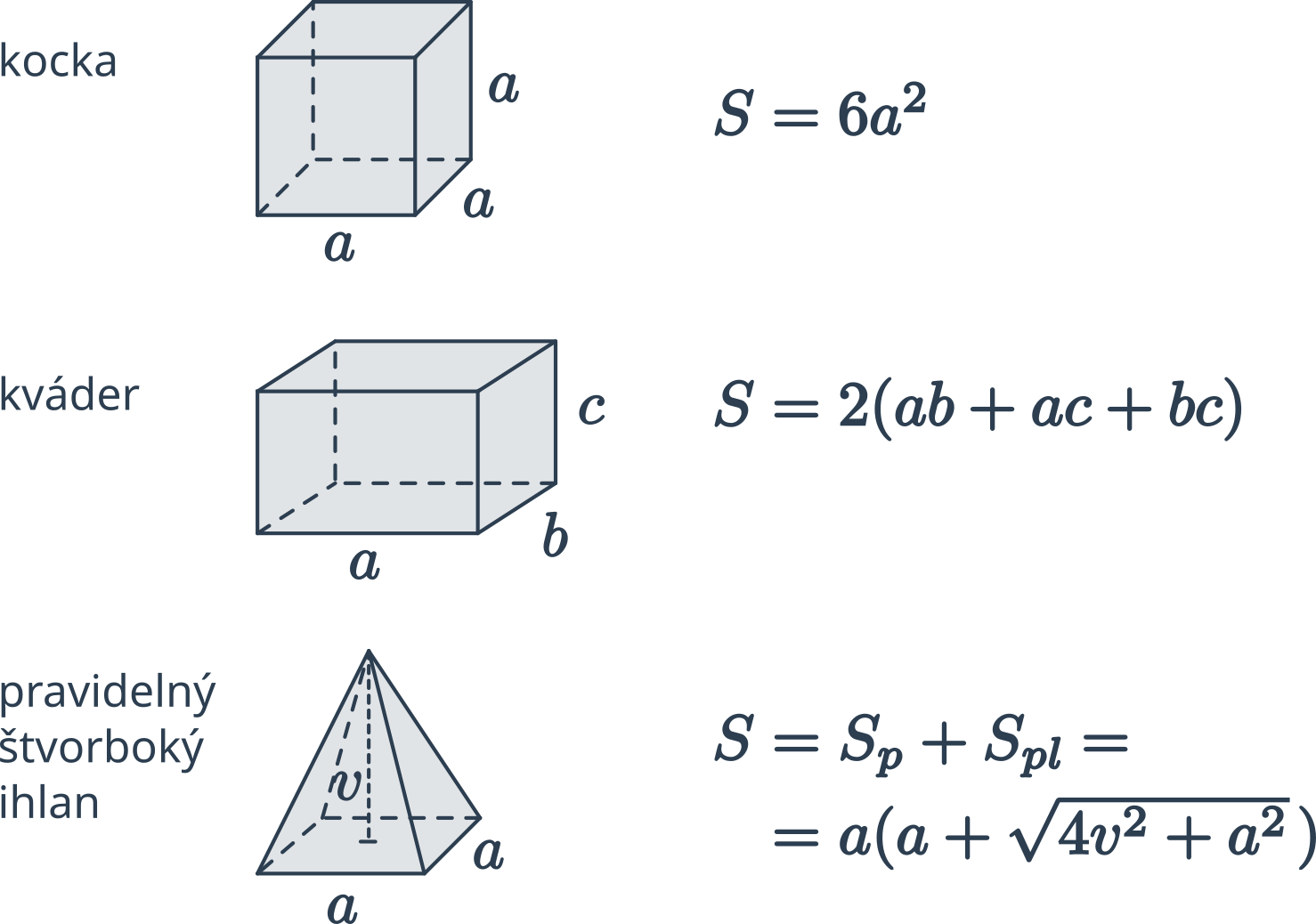
Povrch „hranatých“ telies je jednoducho súčet obsahov jednotlivých strán.
Hranol má dve rovnaké podstavy a plášť, povrch je teda S=2\cdot S_p+S_{pl}. Ihlan má jednu podstavu a plášť, povrch je teda S=S_p+S_{pl}.
Steny kvádra sú obdĺžniky, pričom sú vždy dve rovnako veľké. Povrch teda vypočítame ako S = 2(ab+ac+bc).
Kocka má šesť stien a všetky sú tvorené rovnakým štvorcom. Povrch je S=6a^2.
Povrch okrúhlych telies
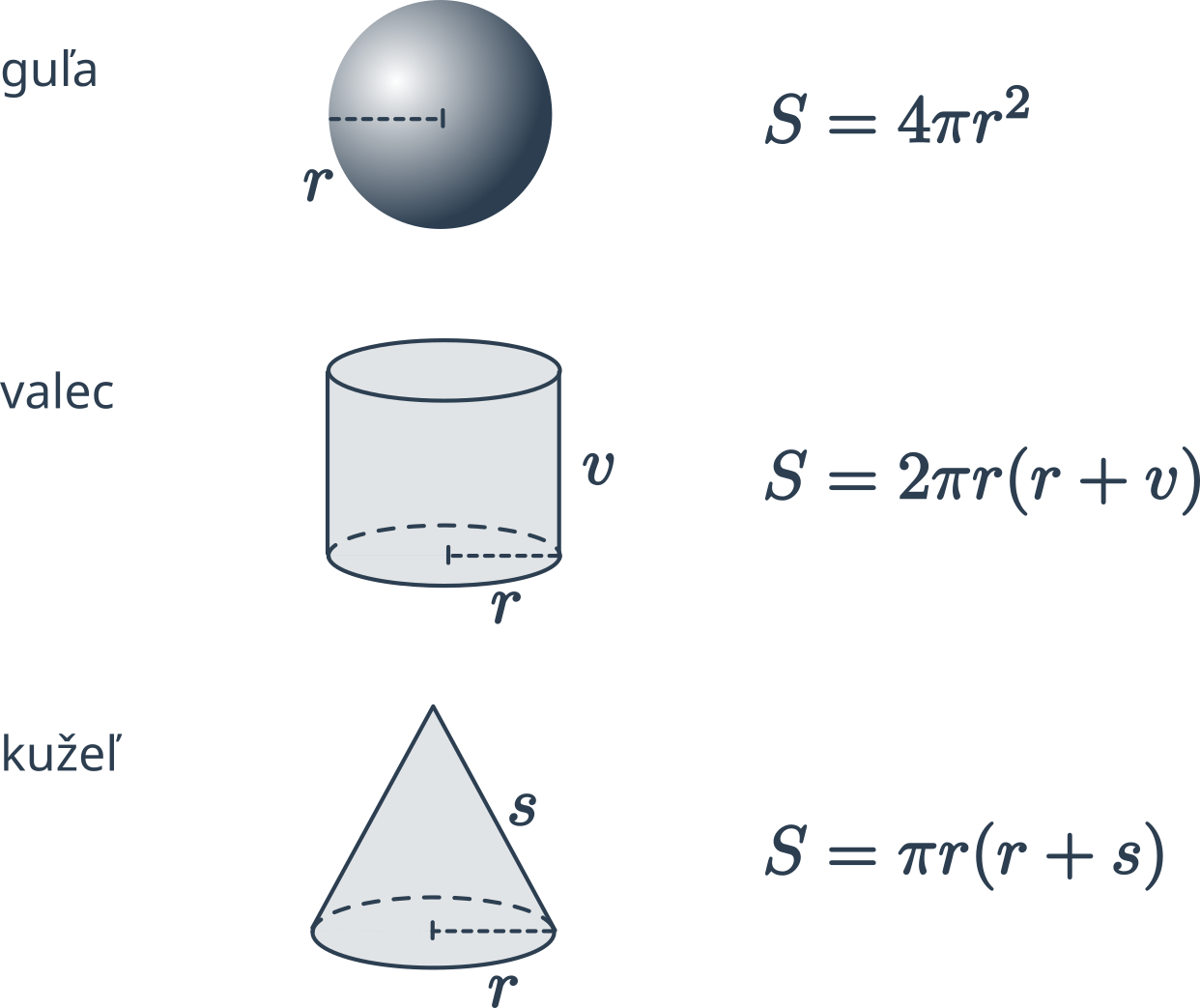
Povrch „guľatých“ telies vypočítame s využitím konštanty \pi \approx 3{,}14159265. Vo vzorcoch označuje r polomer (gule či podstavy), v výšku valca, s stranu kužeľa.
- Povrch gule je S = 4\pi r^2.
- Povrch valca sa skladá z podstavy (dvakrát) a plášťa: S = 2\cdot \pi r^2 + 2\pi r v = 2\pi r (r+v).
- Povrch kužeľa sa skládá z podstavy a plášťa: S = \pi r^2 + \pi rs= \pi r(r+s).
Objem hranatých telies
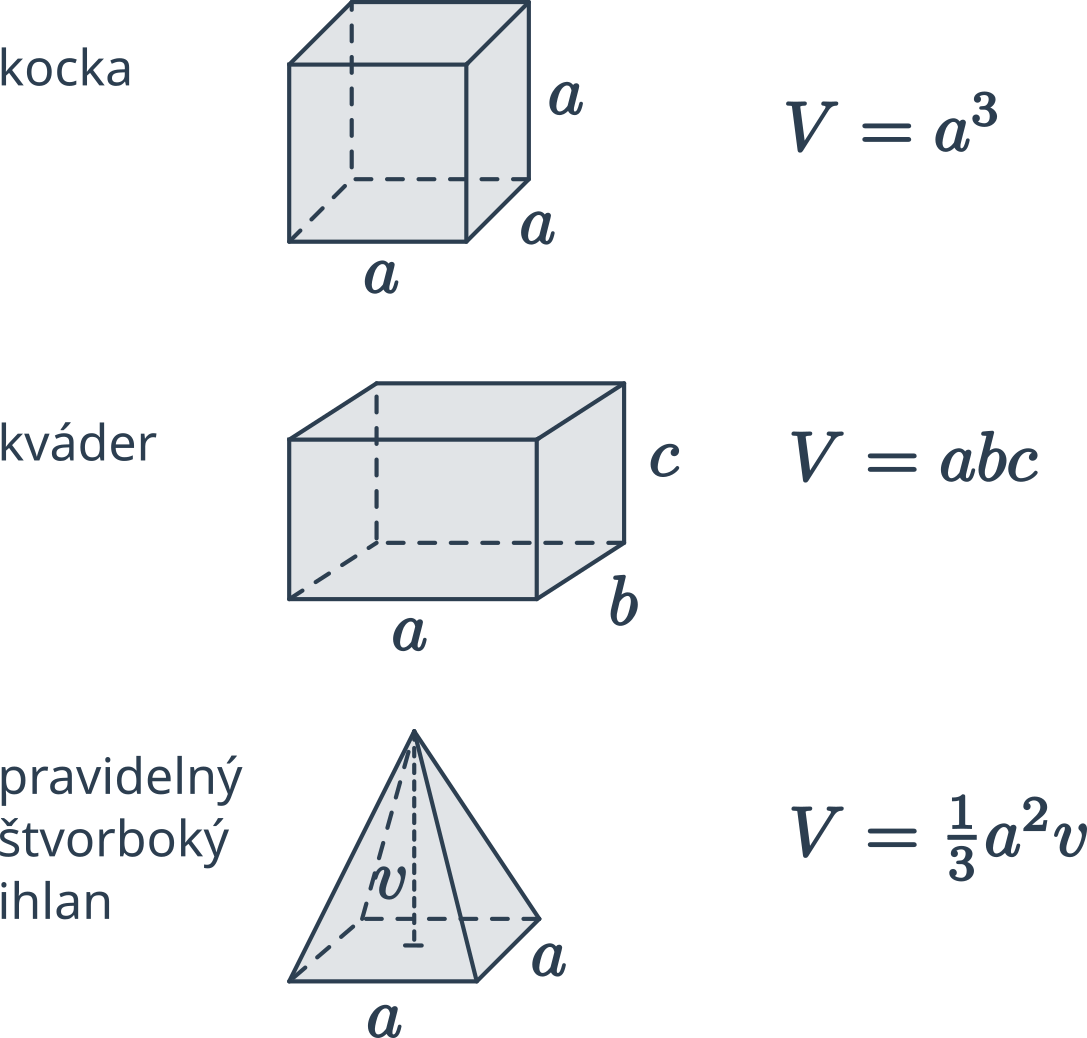
Vzorce pre objem „hranatých“ telies vychádzajú z obsahu podstavy a výšky telesa.
Objem ľubovoľného hranola je súčin obsahu podstavy a výšky: V=S_p\cdot v.
Kváder a kocka sú špeciálne prípady hranola, ktorých podstava je obdĺžnik (štvorec) a výška je zvyšná hrana. Objem kvádra je teda súčin dĺžok jeho hrán: V = abc. Objem kocky vypočítame rovnakým spôsobom. Keďže sú v kocke všetky hrany rovnako dlhé, výraz sa zjednoduší na V = a^3.
Objem ihlanu je jedna tretina súčinu obsahu podstavy a výšky, teda V=\frac{1}{3}S_p\cdot v. Pre pravideľný štvorboký ihlan potom teda V=\frac{1}{3} a^2v.
Príklady:
- Kocka s hranou 4 m má objem V = 4^3 = 64 m³.
- Kváder s hranami 3, 6 a 10 cm má objem V = 3\cdot 6 \cdot 10 = 180 cm³.
- Pravidelný štvorboký ihlan s podstavou s hranou 6 cm a výškou 4 cm má objem V=\frac{1}{3} 6^2 \cdot 4 = 48 cm³.
Objem okrúhlych telies
Objem „guľatých“ telies vypočítame s využitím konštanty \pi \approx 3{,}14159265. Vo vzorcoch označuje r polomer (gule či podstavy) a v výšku valca.
- Objem gule je V = \frac43 \pi r^3.
- Objem valca je obsah (kruhovej) podstavy vynásobený výškou, teda V = S_p \cdot v = \pi r^2 v.
- Objem kužeľa je jedna tretina obsahu podstavy vynásobeného výškou, teda V = \frac13 S_p \cdot v = \frac13 \pi r^2 v.
Uhol je časť roviny vymedzená dvomi polpriamkami. Veľkosť uhla meriame najčastejšie v stupňoch, pričom plný uhol má veľkosť 360°. Uhly využívame v mnohých oblastiach geometrie a majú bohaté praktické využitie vo fyzike, navigácii (azimuty) a v podstate kdekoľvek, kde sa niečo stavia.
Pri práci s uhlami je prvý krok základné rozpoznávanie uhlov – potrebujeme získať základnú predstavu o uhloch a schopnosť odhadnúť veľkosť uhlu podľa obrázka. Ďalší krok je potom znalosť pojmov súvisiacich s uhlami, medzi ktoré patrí napríklad uhol ostrý, tupý, pravý, plný, vrcholový alebo striedavý.
Na získanie zbehlosti v práci s uhlami môže poslúžiť atraktívne cvičenie Korytnačia grafika na Vieme informatiku.
Keď zvládneme základy práce s uhlami, môžeme sa pustiť do práce s uhlami v rovinových objektoch:
Určovanie uhlov
Plný uhol je 360°. Často používané uhly ukazuje obrázok:
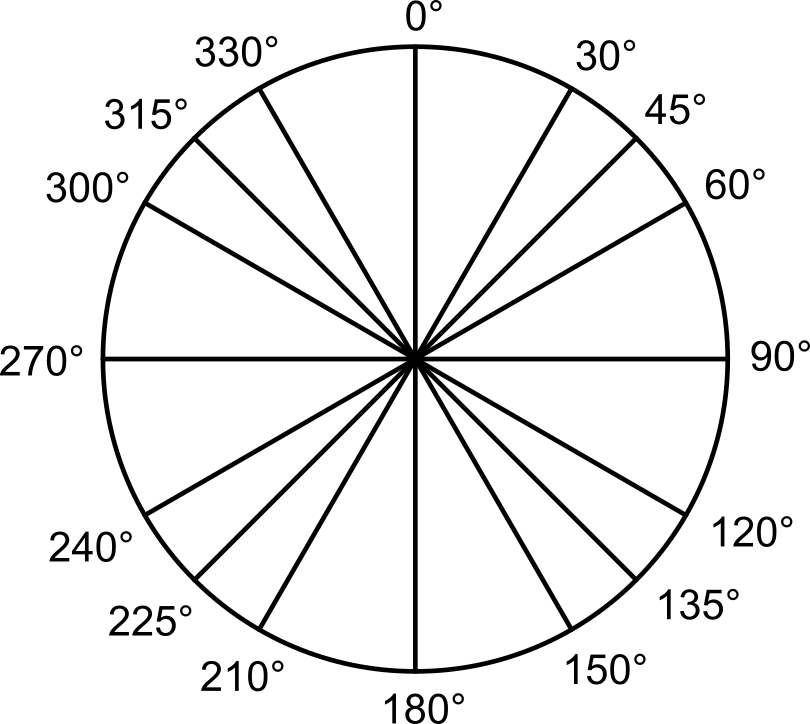
Uhly v trojuholníku
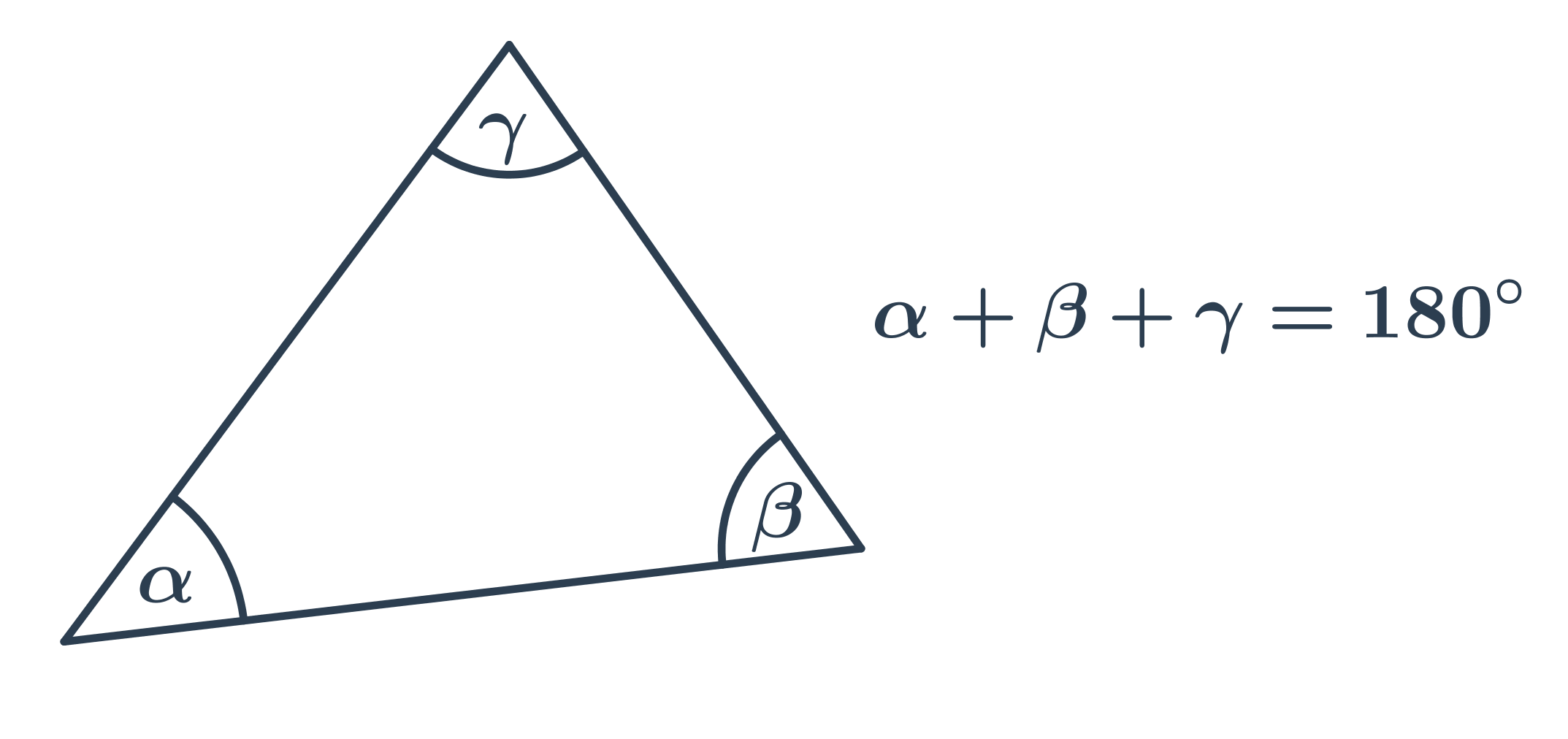
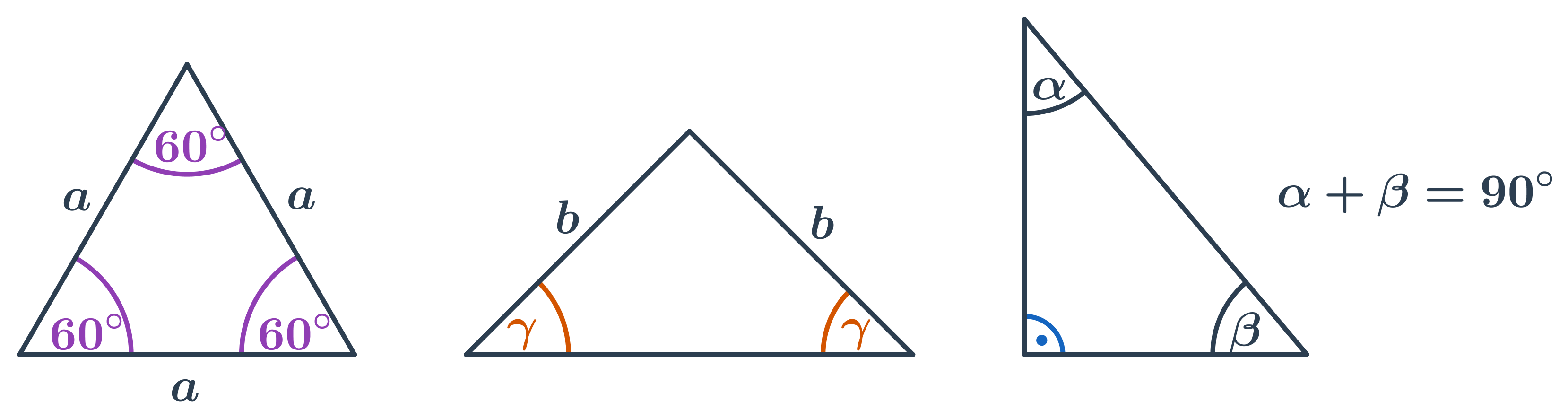
Špeciálne prípady:
- V rovnostrannom trojuholníku majú všetky vnútorné uhly veľkosť 60°.
- V rovnoramennom trojuholníku sú oba uhly pri základni rovnaké.
- V pravouhlom trojuholníku je veľkosť jedného uhla 90°, súčet veľkostí zvyšných dvoch uhlov je tiež 90°.
Pri výpočte je možné využiť aj vrcholových a vedľajších uhlov.
Príklad: Určite veľkosť oranžového uhla.
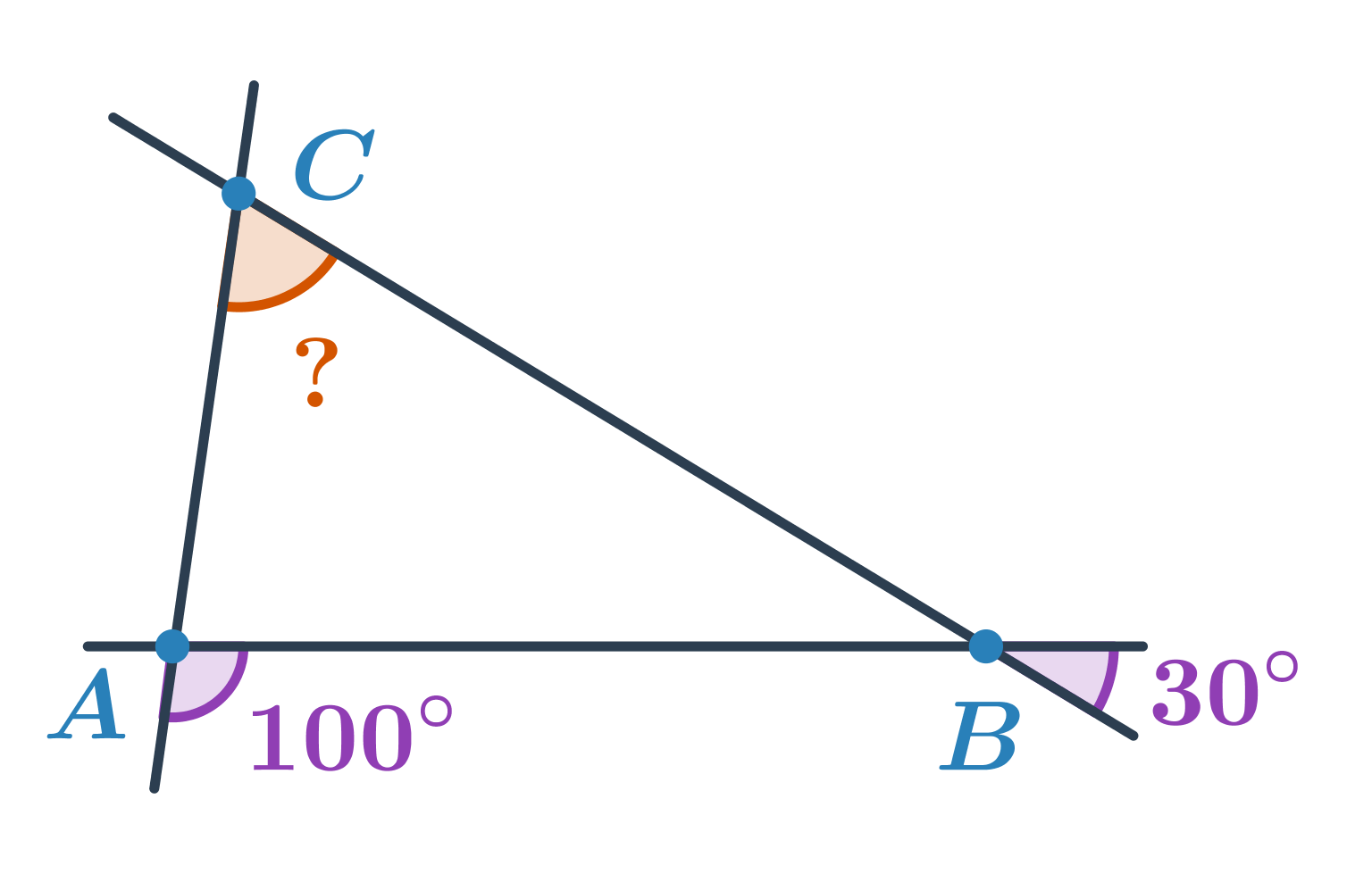
Uhol s vrcholom B tvorí s uhlom s veľkosťou 30° dvojicu vrcholových uhlov. Jeho veľkosť je teda 30°. Uhol pri vrchole A tvorí s uhlom s veľkosťou 100° dvojicu vedľajších uhlov. Jeho veľkosť je teda 180°-100°=80°. Pre veľkosť neznámeho uhla pri vrchole C potom platí: 180°-80°-30°=70°
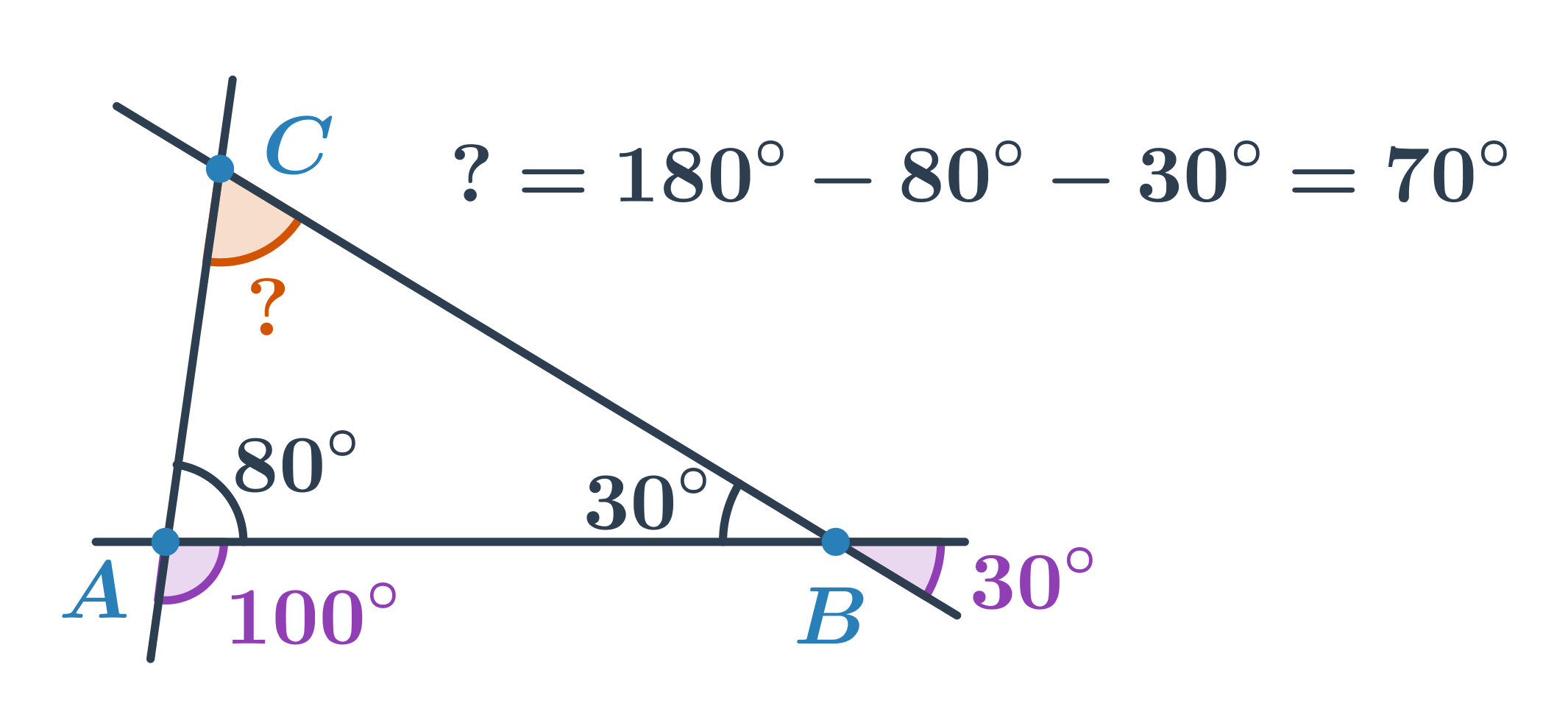
Uhly v štvoruholníku
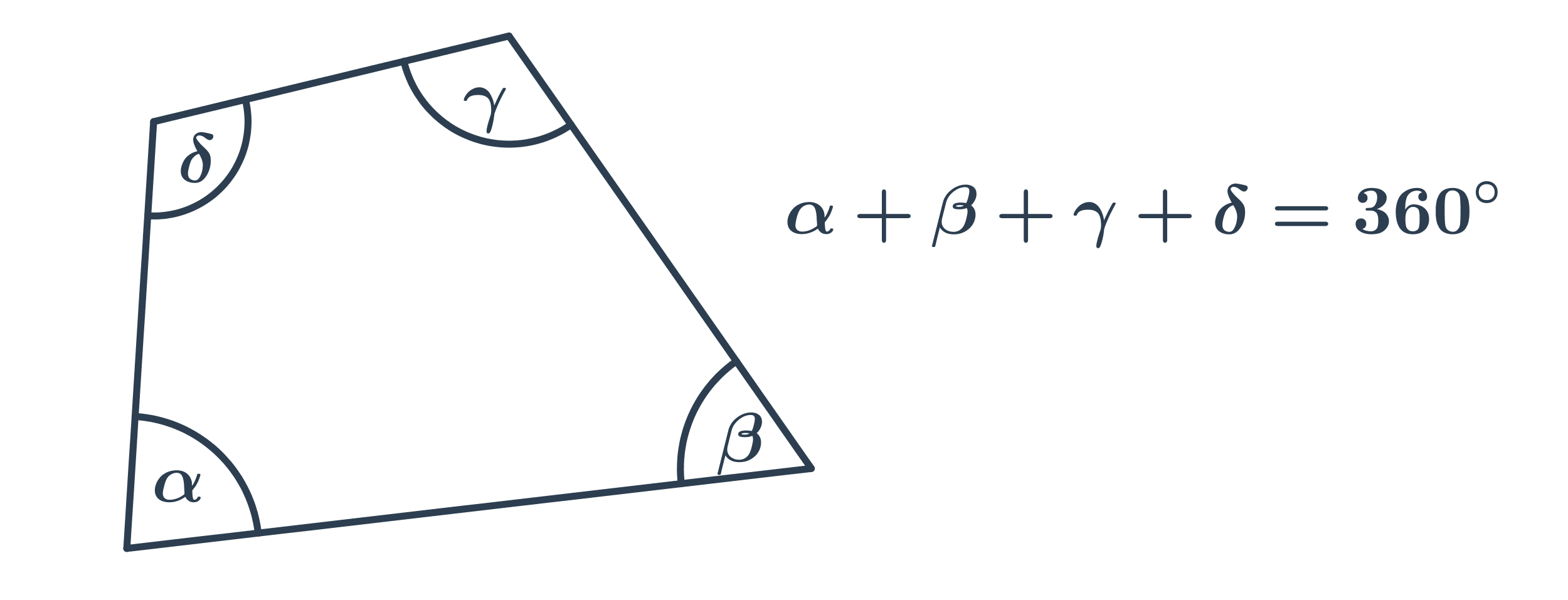
Štvorec, obdĺžnik
- V štvorci aj obdĺžniku je veľkosť všetkých vnútorných uhlov 90°.
- V štvorci zvierajú uhlopriečky uhol s veľkosťou 90°.
Rovnobežník
- Protiľahlé uhly majú rovnakú veľkosť.
- Súčet veľkostí susedných uhlov je 180°.
- Špeciálnym prípadom rovnobežníka je kosoštvorec, ktorého uhlopriečky zvierajú pravý uhol.
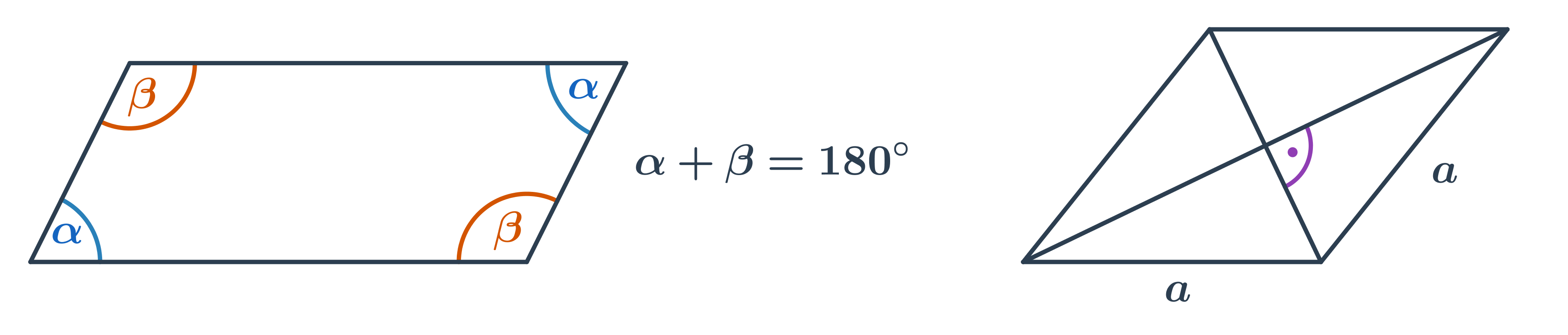
Lichobežník
- Súčet veľkostí vnútorných uhlov pri ramenách je 180°.
- V rovnoramennom lichobežníku sú uhly pri základniach zhodné.
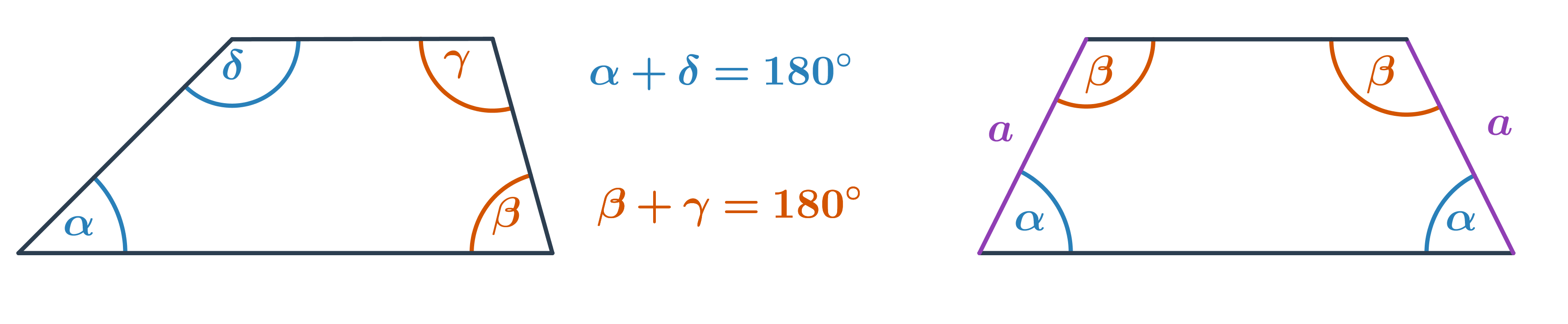
Pri výpočte neznámeho uhla môžeme tiež daný štvoruholník rozdeliť na niekoľko trojuholníkov a tiež je možné využiť aj vrcholové a vedlajšie uhly.
Príklad: Určite veľkosť oranžového uhla v rovnobežníku ABCD.
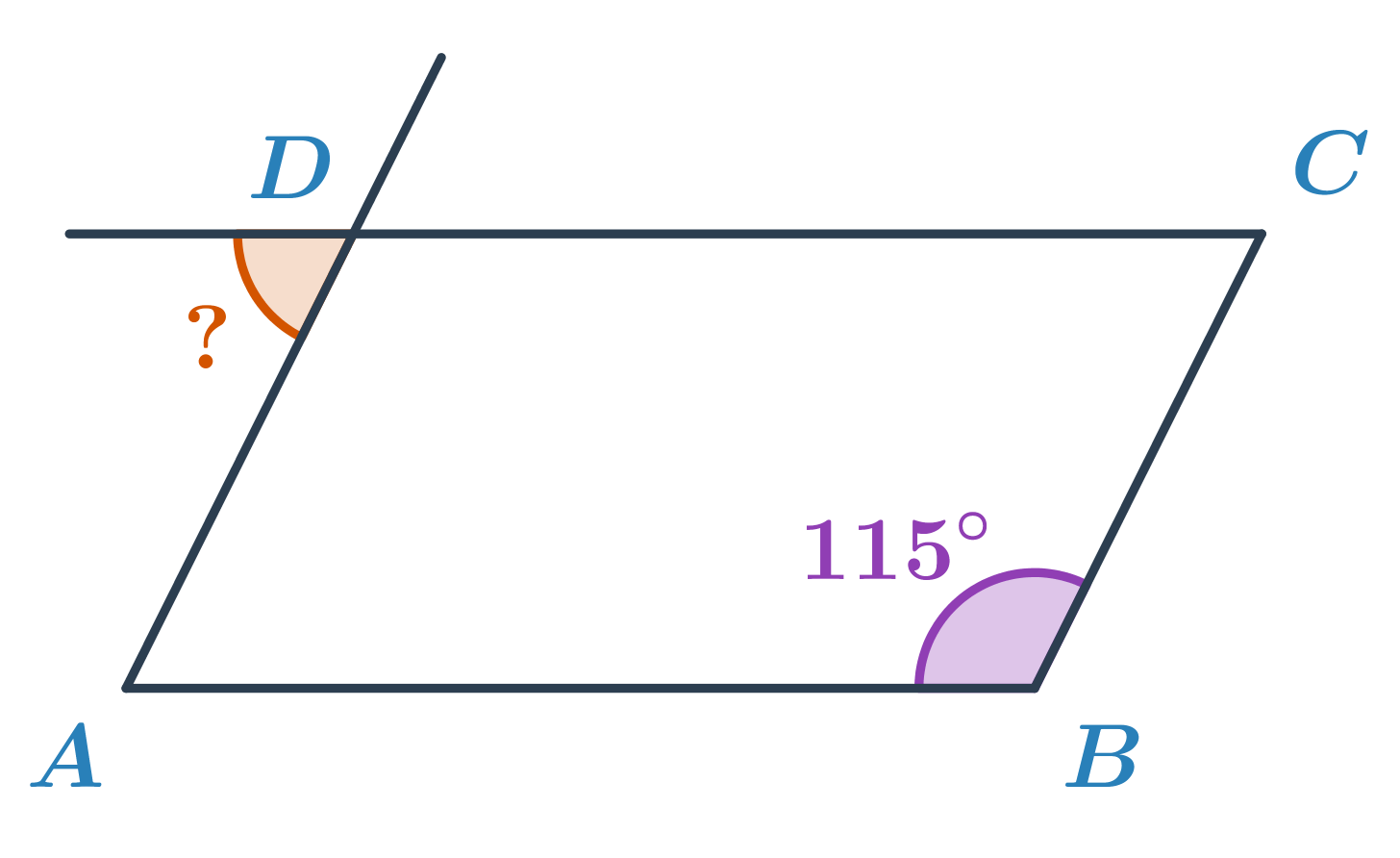
V rovnobežníku majú protiľahké uhly rovnakú veľkosť, uhol ADC má teda veľkosť 115°. Uhol ADC tvorí s neznámym uhlom dvojicu vedľajších uhlov. Veľkosť neznámeho uhla je teda 180°-115°=65°.
Uhly a mnohouholníky
Súčet vnútorných uhlov vo všeobecnom mnohouholníku s n stranami (teda n-uholníku) je 180^\circ\cdot(n-2). Napríklad v päťuholníku je súčet vnútorných uhlov 180^\circ(5-2)=540^\circ. Každý vnútorný uhol potom môže mať inú veľkosť.
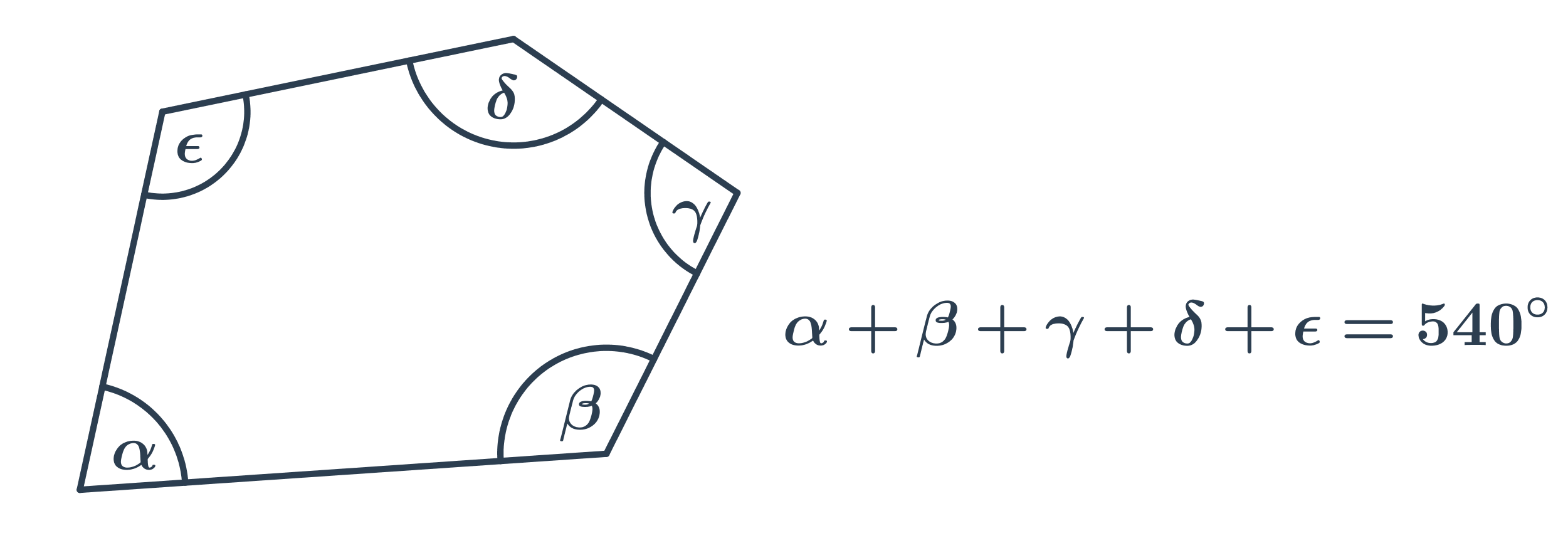
Pravidelné mnohouholníky
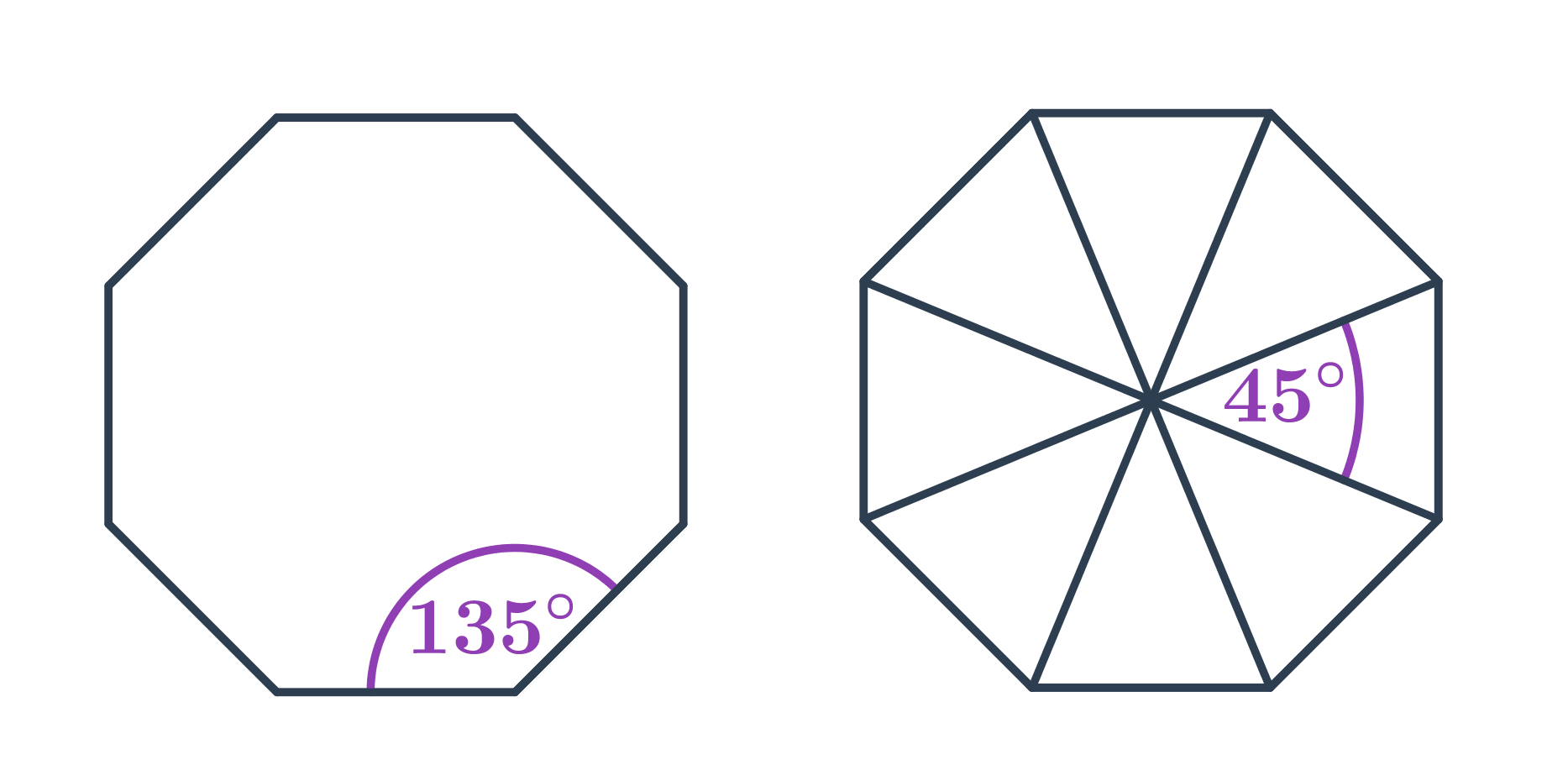
- Každý vnútorný uhol v pravidelnom mnohouholníku s n vrcholmi má veľkosť 180^\circ\cdot\frac{n-2}{n}. Napríklad v pravidelnom osemuholníku má každý vnútorný uhol veľkosť 180^\circ\cdot\frac{8-2}{6}=135^\circ.
- Veľkosť stredového uhla pravidelného n-uholníka je \frac{360^\circ}{n}. Napríklad v pravidelnom osemuholníku má každý stredový uhol veľkosť \frac{360^\circ}{8}=45^\circ.
Pri výpočte neznámeho uhla v mnohouholníku je možné využiť aj vrcholových a vedľajších uhlov.
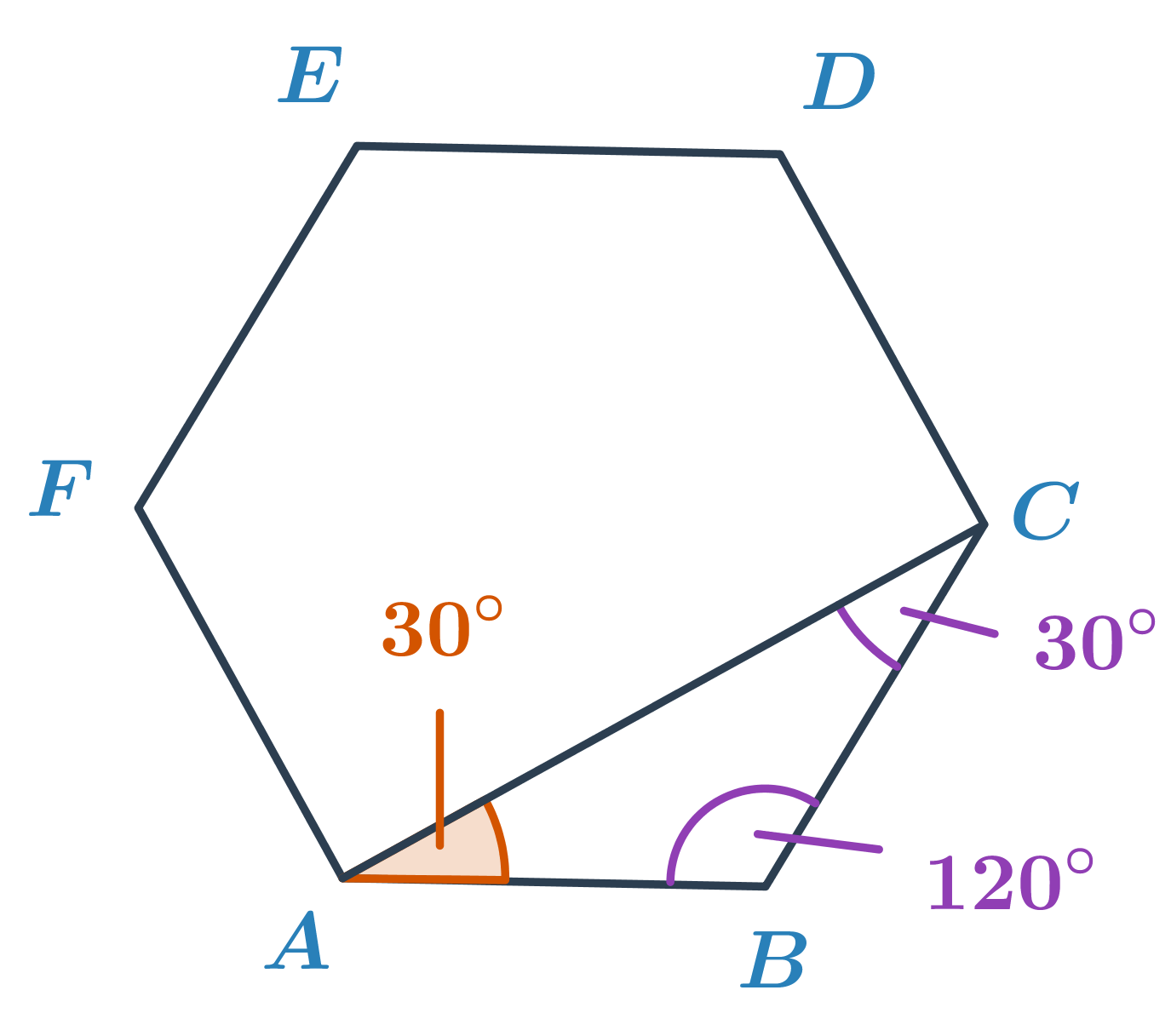
Príklad: Určite veľkosť oranžového uhla v pravidelnom šesťuholníku ABCDEF.
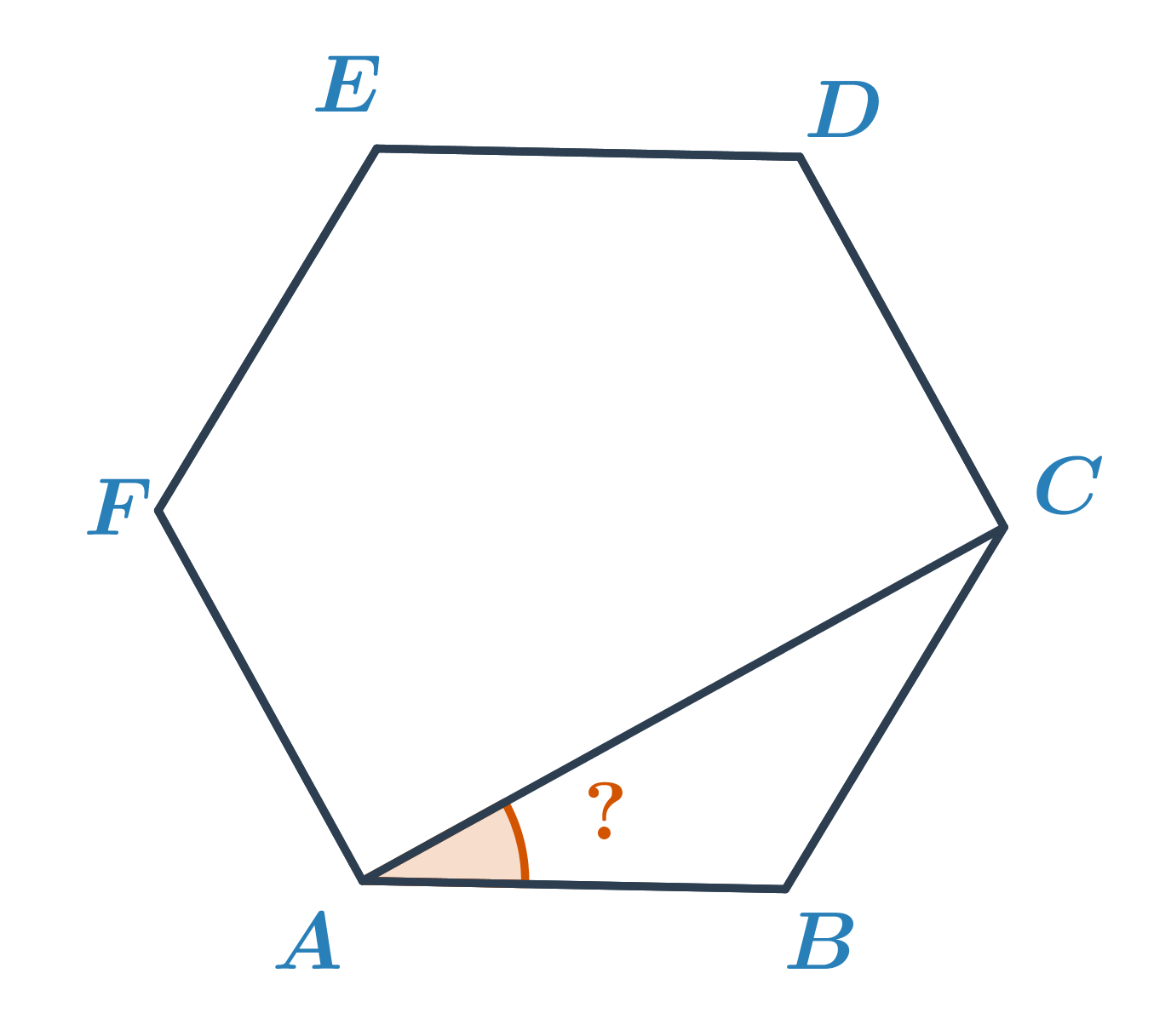
V pravidelnom šesťuholníku má každý uhol rovnakú veľkosť, a to 180^\circ\cdot\frac{6-2}{6}=120^\circ. Uhol ABC má teda veľkosť 120^\circ. Trojuholník ABC je rovnoramenný, uhly pri vrcholoch A a C sú potom zhodné. Ich veľkosť je (180^\circ-120^\circ):2=30^\circ.
Uhly a kružnice
Stredový uhol
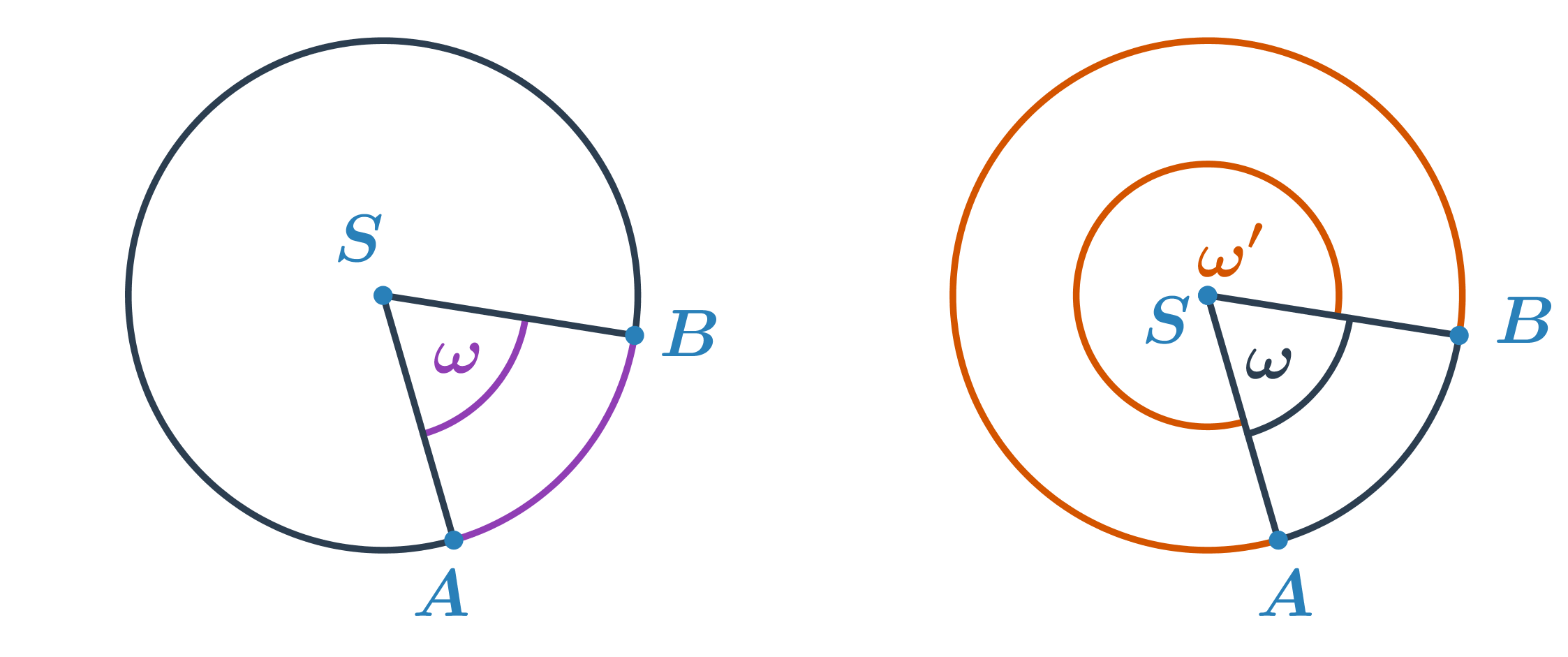
- Uhol s vrcholom v strede S kružnice k, ktorého ramená prechádzajú krajnými bodmi A, B oblúka kružnice k.
- Pre každé dva body na kružnici je možné určiť dva stredové uhly. Každý prináleží tomu oblúku, ktorý v danom uhle leží.
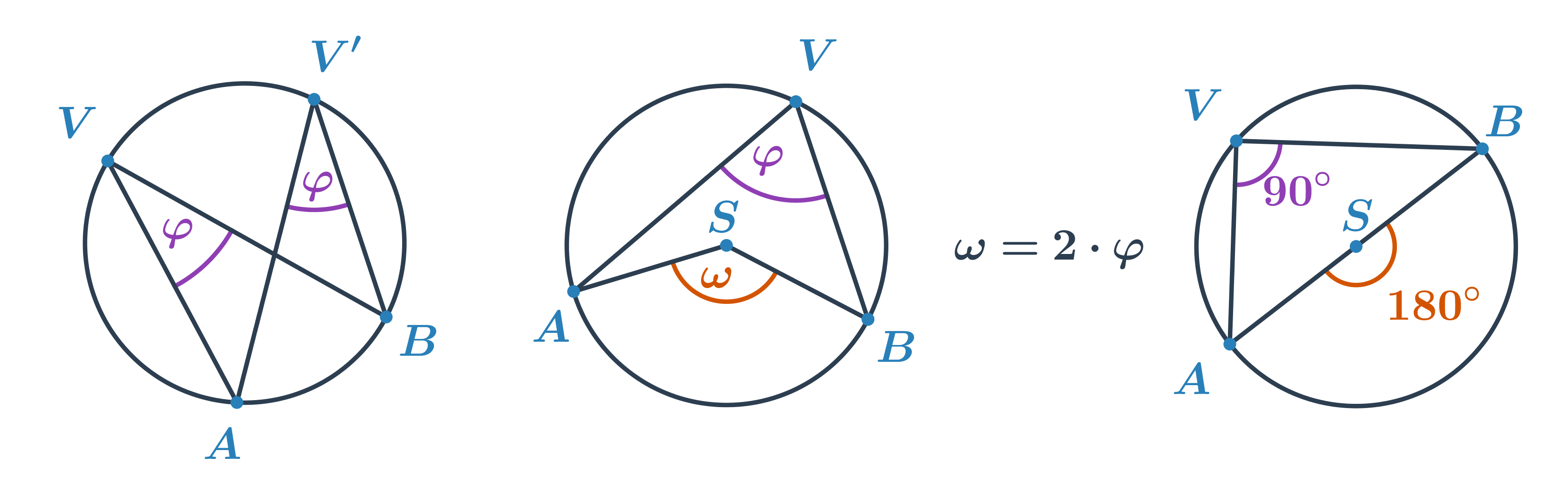
Obvodový uhol
- Uhol, ktorého vrchol V leží na kružnici k a jeho ramená prechádzajú bodmi A, B oblúka kružnice k (A \neq V \neq B)
- Všetky obvodové uhly prináležiace oblúku AB s vrcholom V, ktorý na oblúku neleží, majú rovnakú veľkosť.
- Veľkosť stredového uhla \omega sa rovná dvojnásobku veľkosti obvodového uhla \varphi príslušného k rovnakému oblúku, \omega = 2\cdot\varphi.
- Tálesova veta: Obvodový uhol nad priemerom kružnice je pravý.
Úsekový uhol
- Uhol, ktorý zviera tetiva AB kružnice k s dotyčnicou t kružnice v bode A alebo B.
- Veľkost úsekového uhla je rovnaká ako veľkosť obvodového uhla nad oblúkom AB.
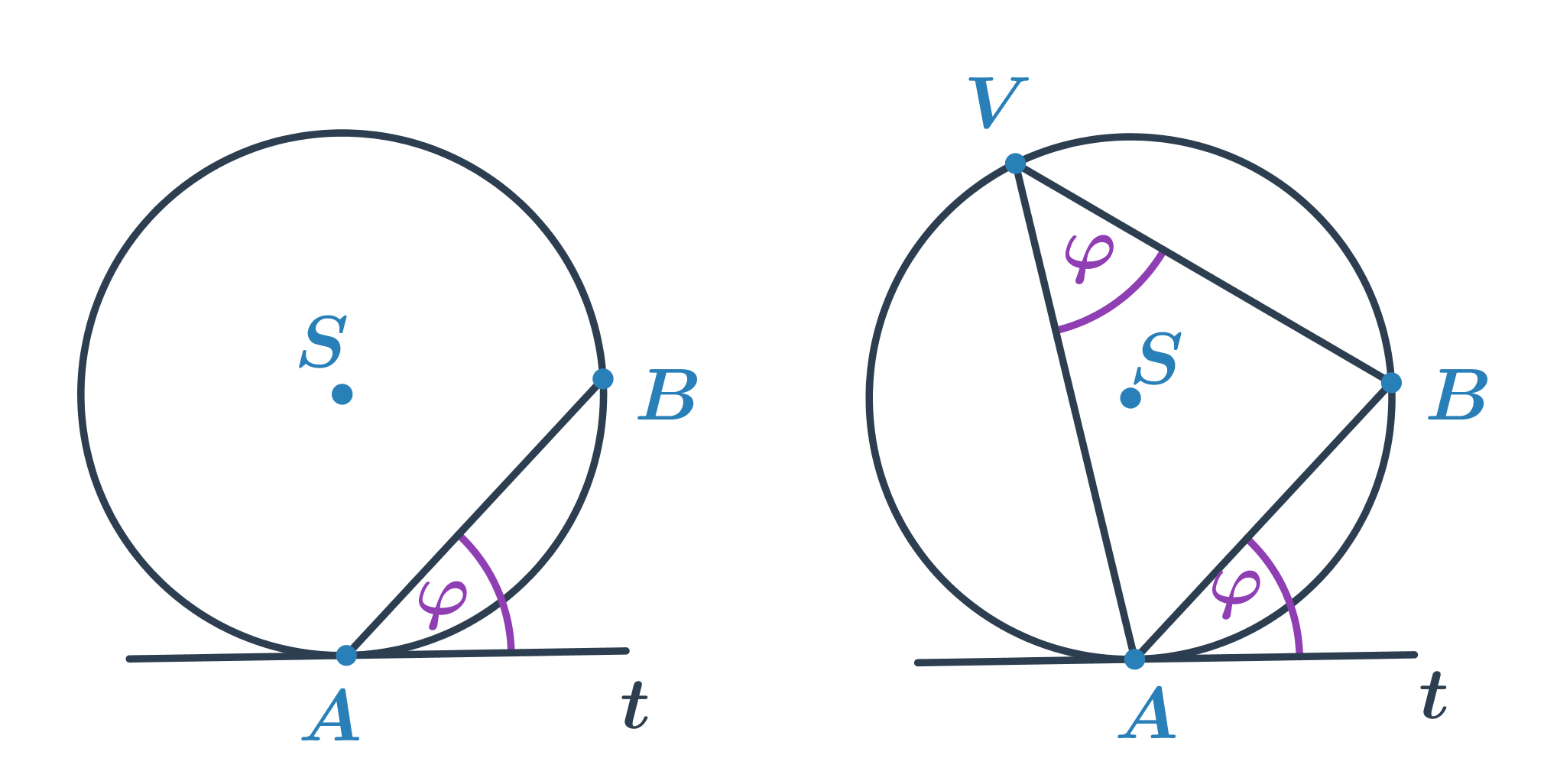
Príklad 1: Určite veľkost oranžového uhla.
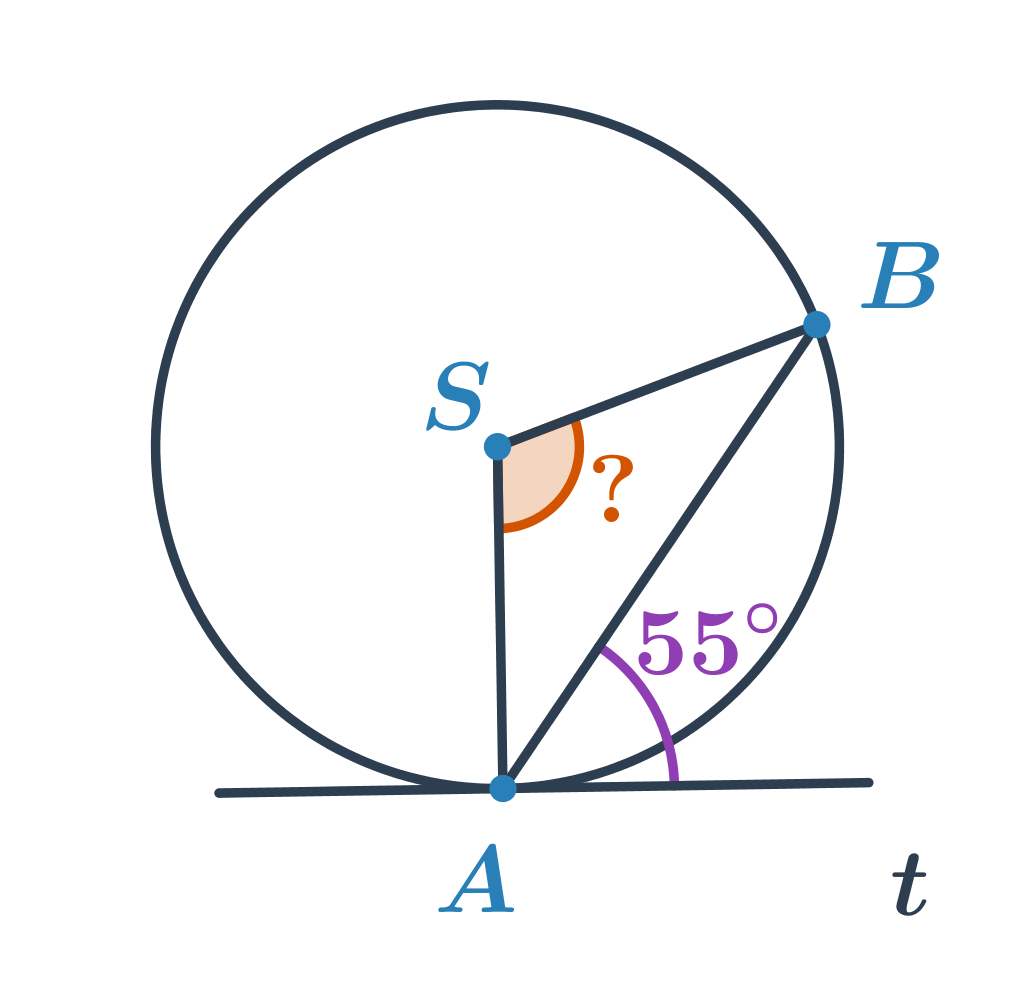
Uhol s veľkosťou 55^\circ je úsekový uhol prináležiaci tetive AB. Vieme, že veľkosti úsekového a príslušného obvodového uhla sú rovnaké, teda 55^\circ. Neznámy uhol je stredový uhol prináležiaci menšiemu oblúku AB. Jeho veľkosť je dvojnásobkom veľkosti obvodového uhla, teda 2\cdot55^\circ=110^\circ.
Príklad 2: Určite veľkosť oranžového uhla.
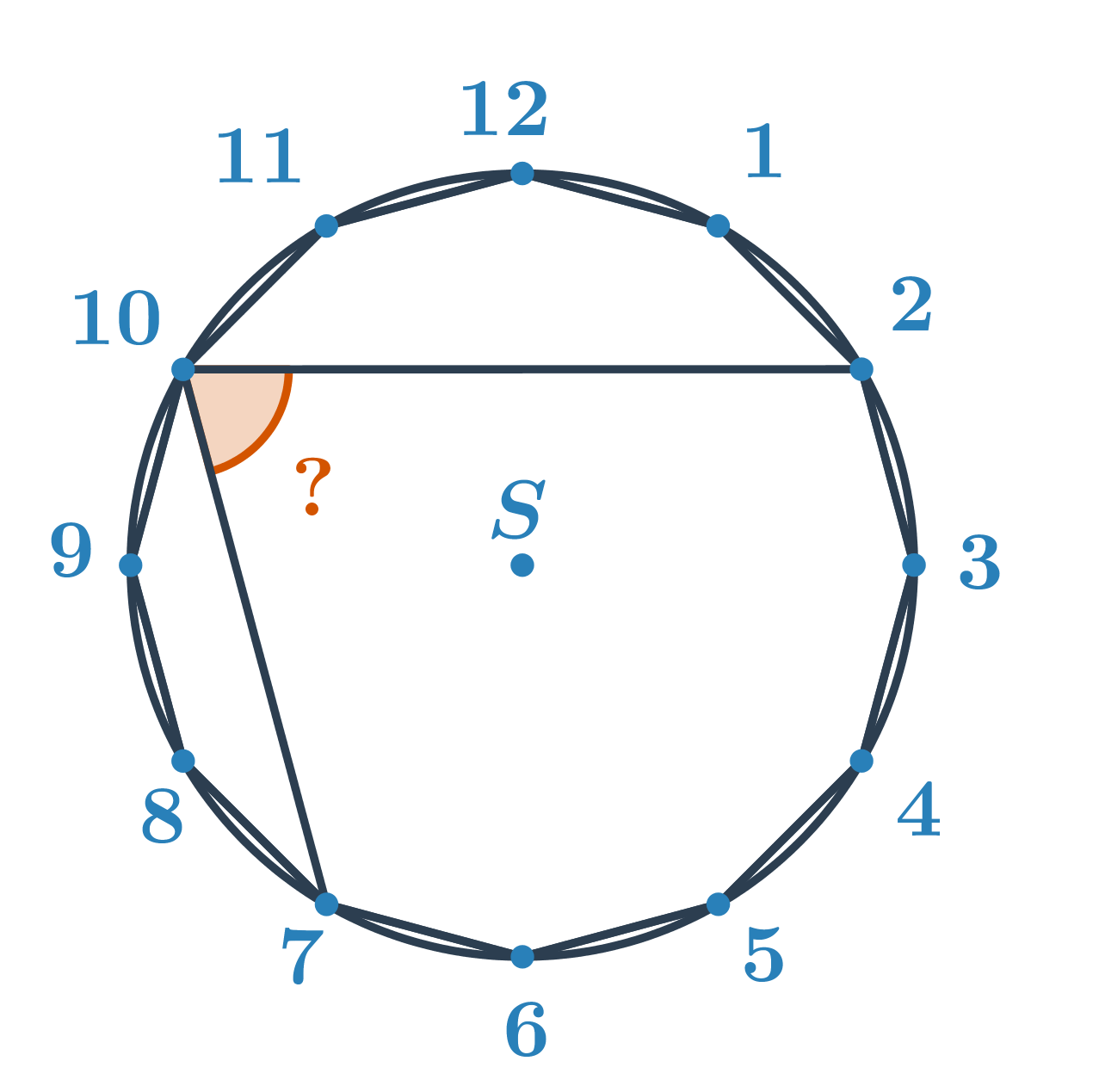
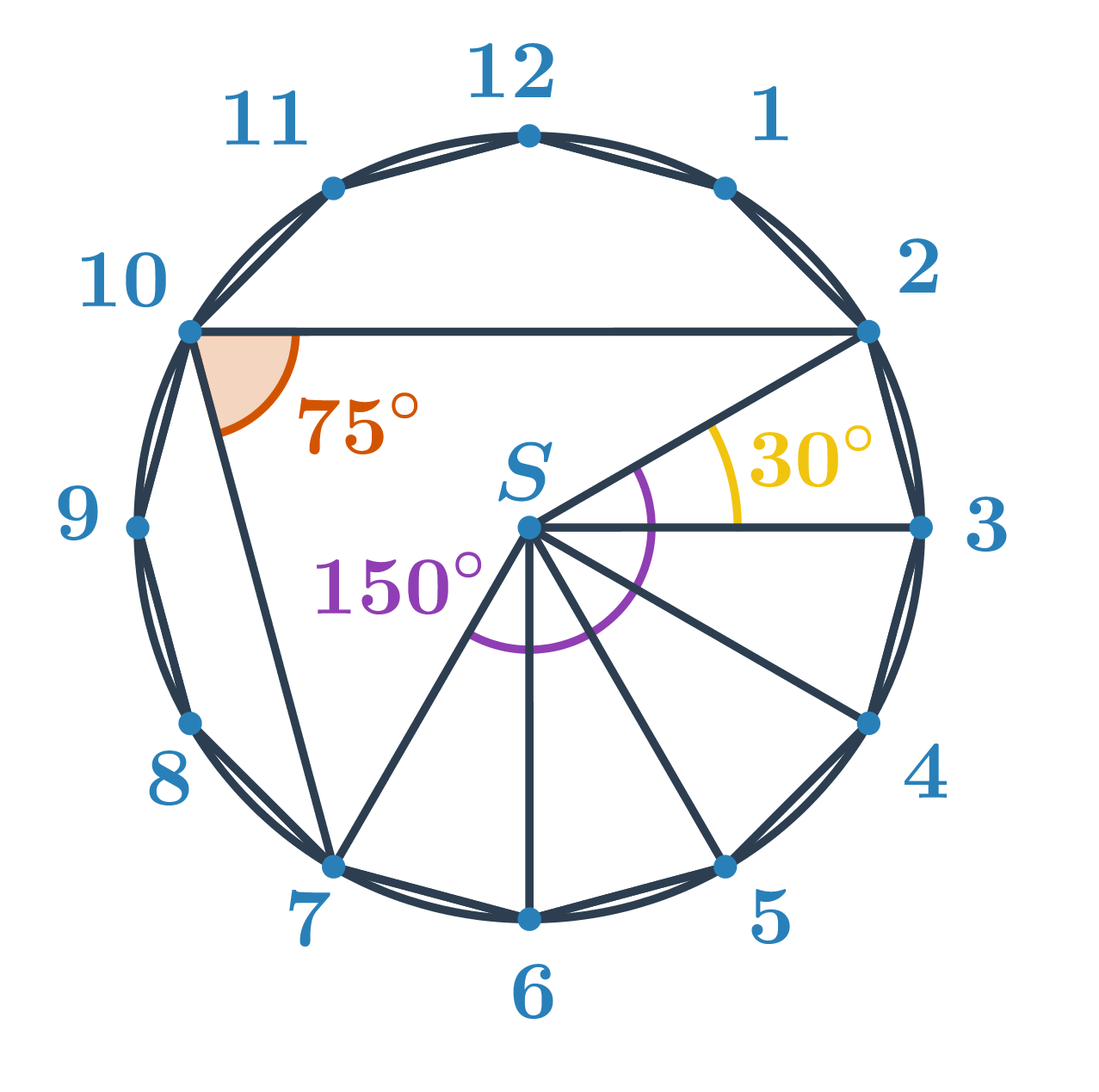
Neznámy uhol je obvodovým uhlom nad menším oblúkom s koncovými bodmi 2 a 7. Určíme veľkosť príslušného stredového uhla. Z kapitoly uhly a mnohouholníky vieme, že veľkosť stredového uhla pravidelného n-uholníka je \frac{360^\circ}{n}. Pre pravidelný dvanásťuholník je teda uhol medzi spojnicami dvoch vedľajších vrcholov a stredu \frac{360^\circ}{12}=30^\circ. Stredový uhol príslušný oblúku 2 a 7 je potom 5\cdot30^\circ=150^\circ. Hľadaný obvodový uhol má polovičnú veľkosť, teda 150^\circ:2=75^\circ.
Geometrické konštrukcie
Ako konštručnú úlohu chápeme takú, v ktorej chceme zostrojiť určitý geometrický útvar (aspoň jeden, prípadne všetky) spĺňajúci dané podmienky. Inými slovami, pomocou pravítka, kružidla a prípadne aj uhlomeru zostrojíme geometrický útvar (trojuholník, obdĺžnik atď.), pre ktorý poznáme dĺžky jeho strán, veľkosti uhlov či iné vlastnosti.
Pred rysovaním je dobré si ujasniť:
- body značíme veľkými písmenami, napr. bod A
- priamky značíme malými písmenami, napr. priamka p
Riešenie konštrukčnej úlohy sa väčšinou skladá z niekoľkých krokov.
Náčrtok: Od ruky si nakreslíme obrázok hľadaného útvaru so všetkým, čo poznáme zo zadania. To nám pomôže predstaviť si výsledok. V rámci prehľadnosti si môžeme jednotlivé prvky vyznačiť farebne. Nezabudnite, náčrtky robíme veľké a prehľadné, aby sme v nich všetko pekne videli.
Popis konštrukcie: Popis jednotlivých krokov, ktoré musíme urobiť, aby sme dospeli k výsledku. Popis píšeme preto, aby každý mohol náš postup zopakovať. Z výsledného obrázku to nie je vždy ľahko možné. Pre zápis konštrukcie používame geometrické značenie. Popis konštrukcie väčšinou riešime až vo vyšších ročníkoch.
Konštrukcia: Je rysovanie príkladu.
Skúška správnosti: Mali by sme si overiť, či obrázok skutočne spĺňa všetky podmienky zo zadania.
Počet riešení (diskusia): Zistíme počet výsledkov, ktoré vyhovujú zadaniu úlohy. Nie vždy musíme všetky výsledky narysovať.
Geometrické konštrukcie: značenie
| Značka | Význam |
|---|---|
| p \parallel q | rovnobežné priamky |
| p \perp q | kolmé priamky |
| \sphericalangle BAC | uhol pri vrchole A |
| \triangle ABC | trojuholník ABC |
| \vert AB\vert | dĺžka úsečky AB |
| A \in p | A leží na priamke p |
| A \notin p | A neleží na priamke p |
| \leftrightarrow AB | priamka prechádzajúca bodmi A, B |
| \mapsto AB | polpriamka začínajúca v bode A, prechádzajúca bodom B |
| \mapsto ABC | polrovina s hraničnou priamkou AB, obsahujúca bod C |
| \mapsto pK | polrovina s hraničnou priamkou p, obsahujúca bod K |
| \leftrightarrow ABC | rovina určená bodmi A, B, C |
| (p, q) | pás roviny, ohraničený rovnobežkami p, q |
Ďalej využívame pre zápis geometrických konštrukcií množinové operácie, predovšetkým prienik (\cap) a zjednotenie (\cup).
Polpriamky a polroviny
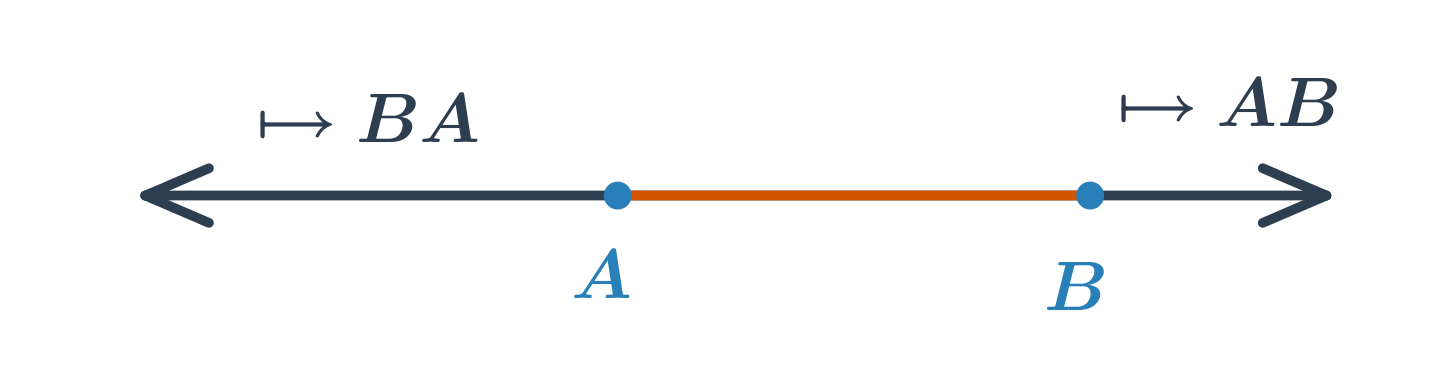
Polpriamka je časť priamky, ktorá vznikne rozdelením priamky jedným jej bodom. Tento bod sa nazývá počiatočný. Polopriamku s počiatočným bodom A prechádzajúcu bodom B značíme \mapsto AB. Každý bod rozdeluje priamku na dve opačné polpriamky so spoločným počiatočným bodom.
Základné vlastnosti * Zjednotením dvoch opačných polpriamok je priamka. * Prienikom dvoch opačných polpriamok je bod. * Prienikom polpriamok \mapsto AB a \mapsto BA je úsečka AB.
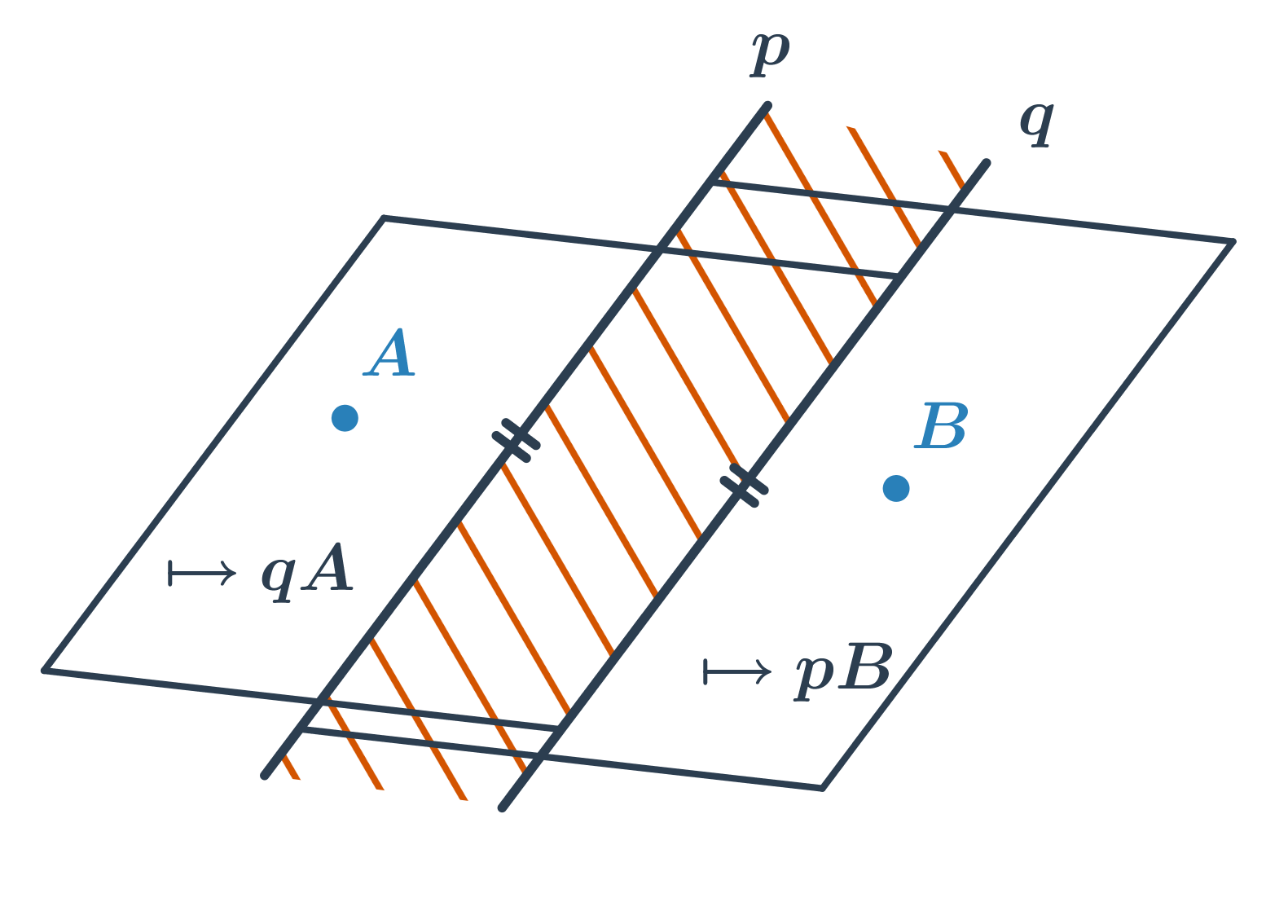
Polrovina je časť roviny, ktorá vznikne rozdelením roviny jednou priamkou. Táto priamka sa nazýva hraničná. Polrovinu s hraničnou priamkou p prechádzajúcu bodom K značíme \mapsto pK. Ak je priamka p určená bodmi A, B, môžeme tiež písať \mapsto ABK. Každá priamka rozdeluje rovinu na dve opačné polroviny so spoločnou hraničnou priamkou.
Základné vlastnosti * Zjednotením dvoch opačných polrovín je rovina. * Prienikom dvoch opačných polrovín je hraničná priamka. * Prienikom dvoch polrovín s rovnobežnými hraničnými priamkami je pás rovnobežiek.
Pre zápis geometrických konštrukcií používame množinové operácie, hlavne prienik (\cap) a zjednotenie (\cup).
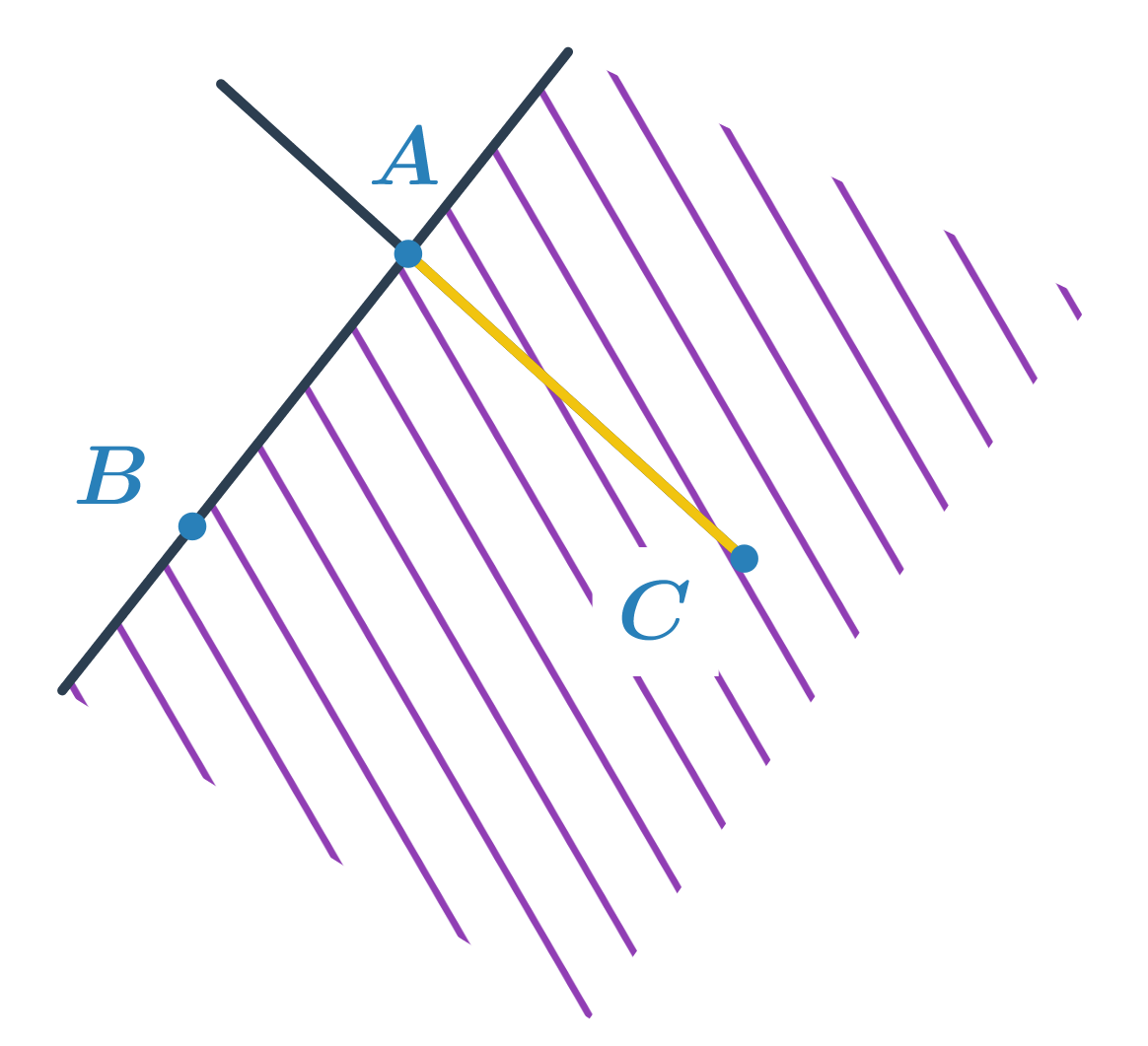
Príklad: Rozhodnite, čo je prienikom polpriamky CA a polroviny ABC.
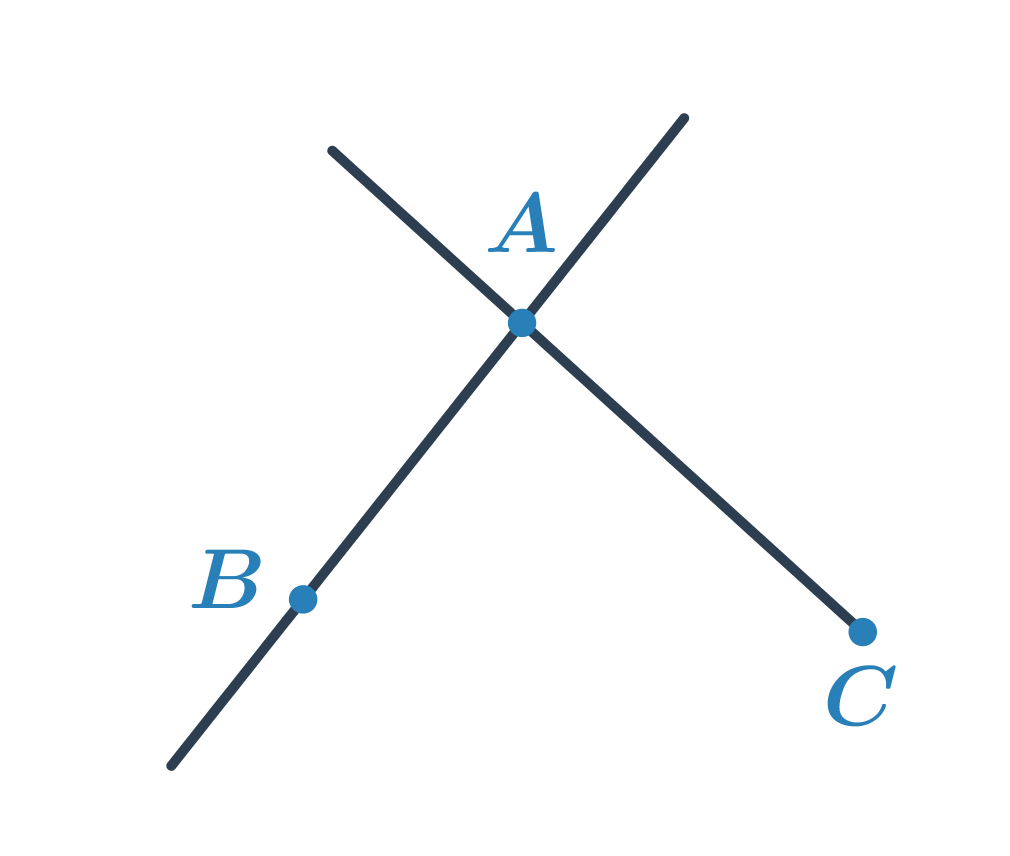
Polrovina ABC je určená hraničnou priamkou AB a bodom C. Polpriamka CA má počiatočný bod C a prechádza bodom A. Prienikom je potom úsečka AC. Matematicky by sme úlohu zapísali: AC = \mapsto ABC \cap \mapsto CA.
Rovnobežky a kolmice
Rovnobežky sú dve priamky ležiace v rovnakej rovine, ktoré sa nikde nepretínajú. Rovnobežnosť priamok p a q zapisujeme p \parallel q.
Kolmica je priamka, ktorá pretína inú priamku a zviera s ňou uhol 90°. Kolmosť priamok p a q zapisujeme p \perp q.
Dve priamky, ktoré sú kolmé na nejakú tretiu priamku a súčasne obe ležia v jednej rovine, sú rovnobežky.
Konštrukčné úlohy: trojuholníky
Pri riešení jednoduchších úloh zostrojujeme trojuholníky, pre ktoré poznáme dĺžky strán. Nesmieme pritom zabúdať, že platí tzv. trojuholníková nerovnosť, teda že súčet dvoch strán je väčší než tretia strana. Jednoducho povedané, ak je súčet dvoch najkratších strán väčší než tretia strana, trojuholník sa dá zostrojiť.
Pri zložitejších príkladoch využívame vety o zostrojiteľnosti trojuholníkov (kde s značí stranu a u uhol):
- Veta sss — v trojuholníku sú dané dĺžky všetkých strán, platí trojuholníková nerovnosť.
- Veta sus — v trojuholníku sú dané dĺžky dvoch strán a veľkosť uhla, ktorý zvierajú (menší než 180°).
- Veta usu — v trojuholníku je daná dĺžka jednej strany a veľkosti 2 uhlov k nej priliehajúcich (súčet veľkostí daných uhlov je menší než 180°).
Tieto vety tiež používame pri určení zhodnosti trojuholníkov.
Pri najťažších príkladoch využívame pri konštrukcii ďalšie pojmy súvisiace s trojuholníkom, napríklad výška, ťažnica, či množiny bodov daných vlastností.
Konstrukčné úlohy prierezovo
Pri riešení zložitejších konštrukčných úloh budeme využívať aj množiny bodov daných vlastností. Pripomeňme si tie najdôležitejšie.
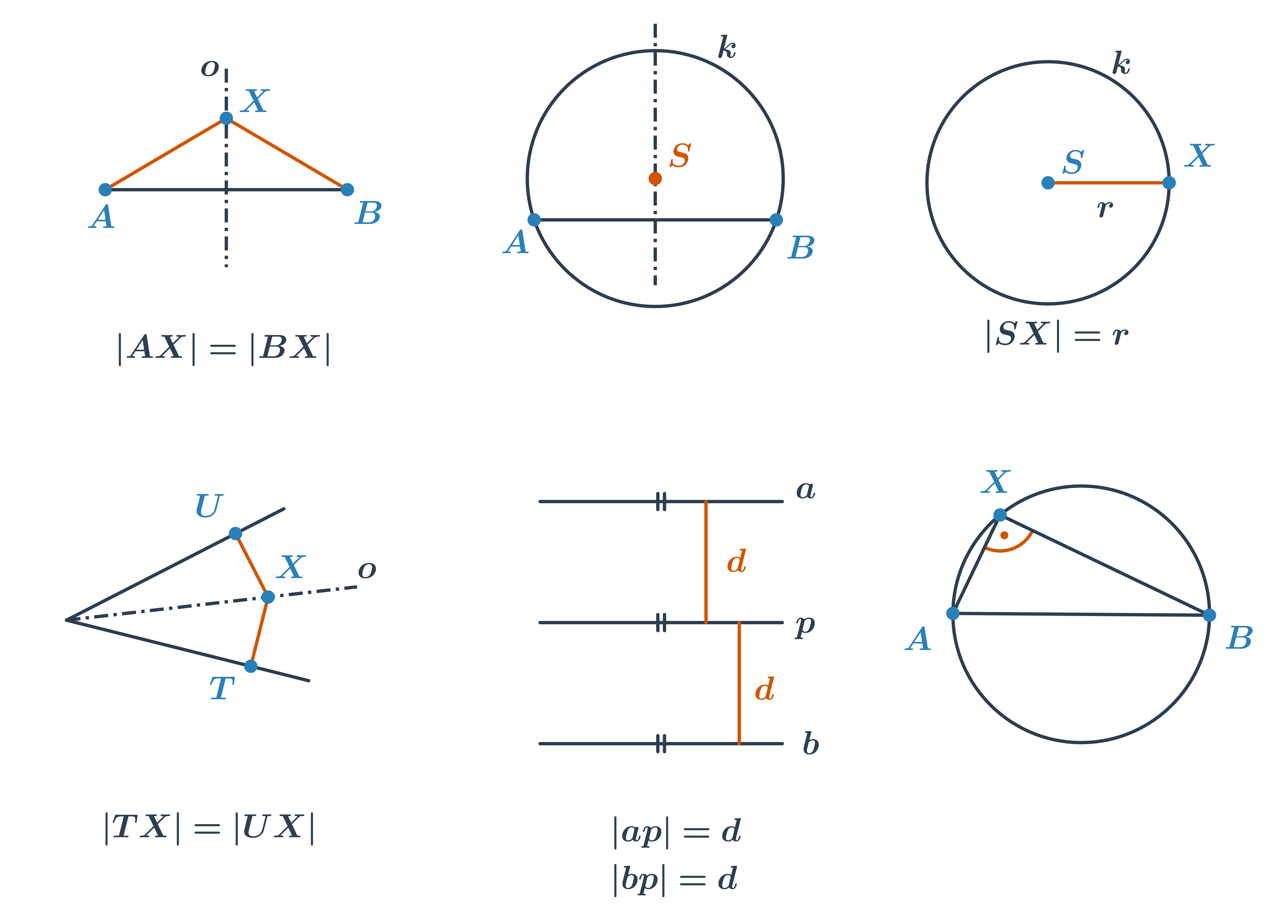
| os úsečky AB | množina všetkých bodov, ktoré majú od bodov A, B rovnakú vzdialenosť |
| os úsečky AB | množina stredov všetkých kružníc, ktoré prechádzajú bodmi A, B |
| kružnica | množina všetkých bodov, ktoré majú od bodu S rovnakú vzdialenosť (polomer r) |
| os uhla | množina všetkých bodov, ktoré majú od ramien uhla rovnakú vzdialenosť |
| rovnobežky | množiny všetkých bodov, ktoré majú od priamky p rovnakú vzdialenosť |
| Tálesova kružnica nad úsečkou AB | množina všetkých vrcholov pravých uhlov, ktorých ramená prechádzajú bodmi A, B |
Operácie a vlastnosti v rovine
Základná intuitívna predstava pre jednotlivé operácie a vlastnosti:
- Osová súmernosť: robíme „zrkadlový“ obraz útvaru podľa priamky.
- Stredová súmernosť: preklápame útvar podľa bodu.
- Rotácia: otočíme útvar okolo určitého bodu o nejaký uhol.
- Zhodnosť: dva útvary sú zhodné, ak „majú rovnaký tvar a veľkosť“ (môžu sa líšiť natočením a umiestnením).
- Podobnosť: dva útvary sú podobné, ak „majú rovnaký tvar“ (môžu sa líšiť veľkosťou, natočením a umiestením).
Téma určenie zobrazení v rovine sa potom zaoberá rozlišovaním medzi jednotlivými zobrazeniami.
Osová súmernosť
Osová súmernosť je daná priamkou o a priraďuje každému bodu X mimo os taký bod X', že priamka o je osou úsečky XX'. Inými slovami: obraz má od osi rovnakú vzdialenosť ako pôvodný bod a spojnica bodov je kolmá na os. Osová súmernosť zachováva vzdialenosti aj uhly, ide teda o druh zhodnosti.
Príklady
Modré a oranžové útvary sú vzájomne osovo súmerné podľa osi o:
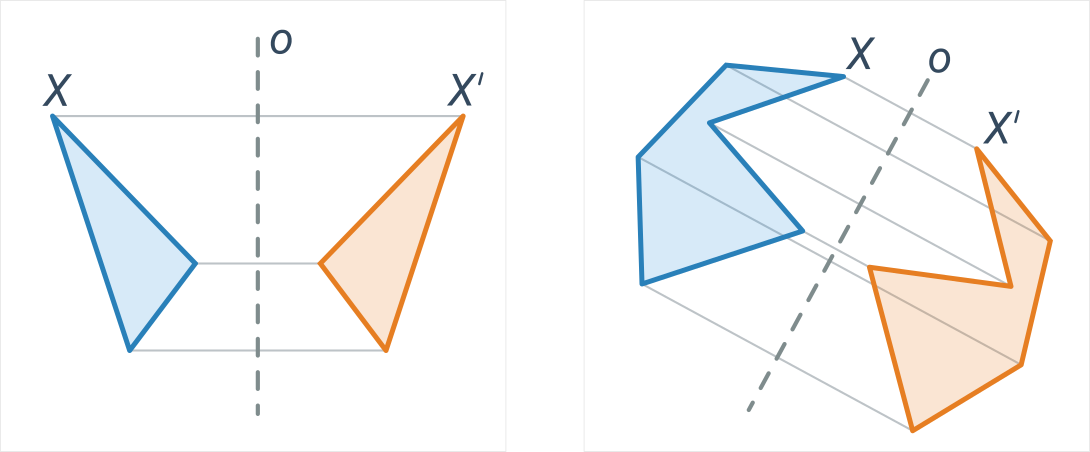
Pre lepšie pochopenie môže byť užitočné porovnať osovú a stredovú súmernosť.
Osovo súmerný útvar
Útvar označujeme za osovo súmerný, ak je v nejakej osovej súmernosti obrazom seba samého. Os tejto súmernosti potom nazývame osou útvaru. Obrázok uvádza príklady útvarov osovo súmerných (zelené, s vyznačenými osami súmernosti) aj tých nesúmerných (červené):
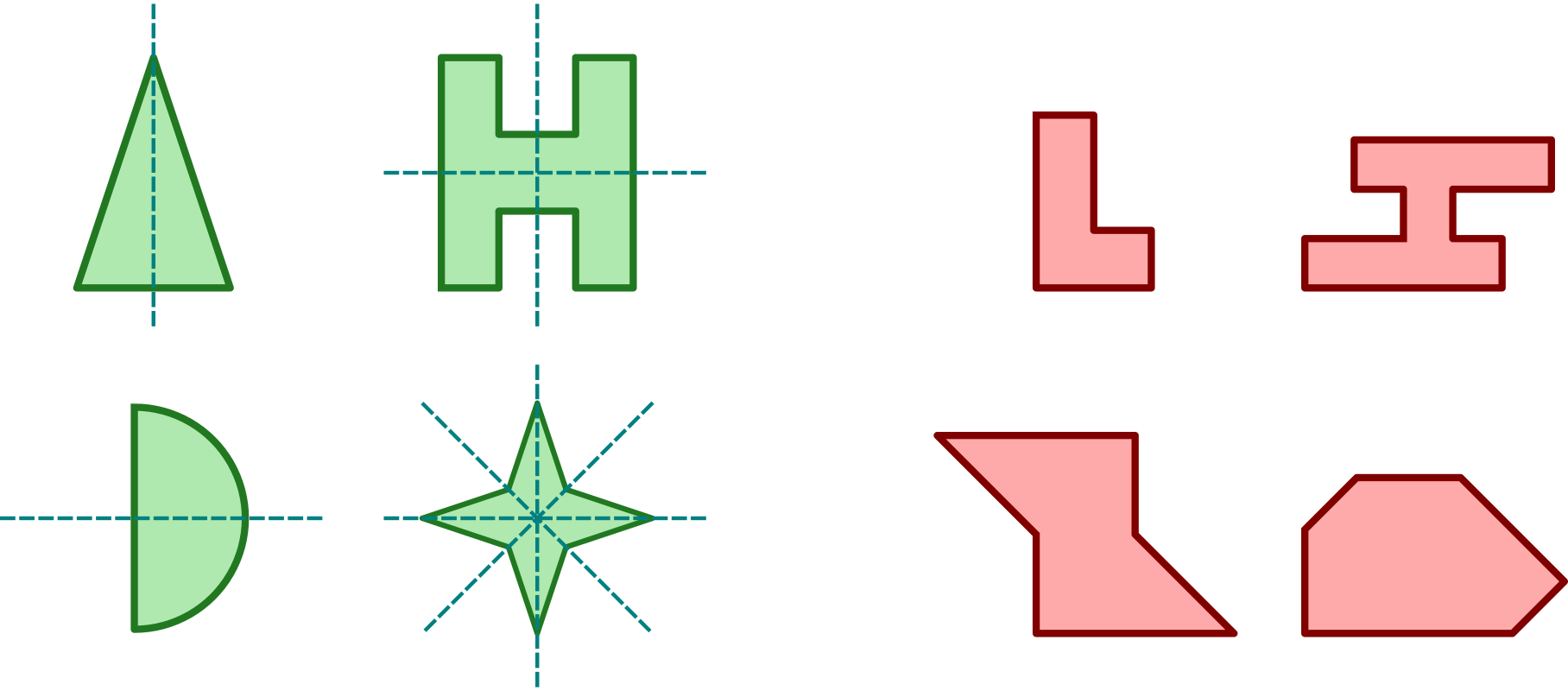
Ďalšie príklady:
- Úsečka je osovo súmerná a má v rovine jedinú os súmernosti (kolmicu v jej strede).
- Rovnoramenný trojuholník je osovo súmerný.
- Trojuholník, ktorý nie je rovnoramenný, nie je osovo súmerný.
- Všetky pravidelné mnohouholníky sú osovo súmerné. Počet osí súmernosti je rovný počtu vrcholov mnohouholníka.
- Kruh je osovo súmerný a má nekonečne veľa osí súmernosti.
Stredová súmernosť
Stredová súmernosť je daná bodom S a priraďuje každému bodu X taký bod X', že bod S je stredom úsečky XX'. Inými slovami: obraz má od stredu rovnakú vzdialenosť ako pôvodný bod a leží na polpriamke opačnej k SX.
Stredová súmernosť zachováva vzdialenosti aj uhly, ide teda o druh zhodnosti. Stredová súmernosť so stredom v bode S je zhodná s otočením o 180 stupňov podľa stredu S.
Príklady
Modré a oranžové útvary sú vzájomne stredovo súmerné podľa stredu S:
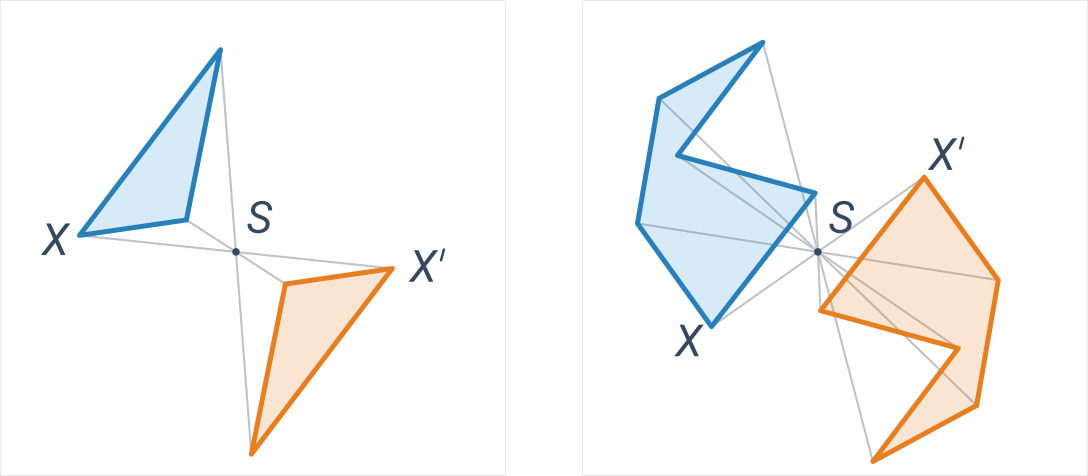
Pre lepšie pochopenie môže byť užitočné porovnať stredovú a osovú súmernosť.
Stredovo súmerný útvar
Útvar označujeme za stredovo súmerný, ak je v nejakej stredovej súmernosti obrazom seba samého. Stred tejto stredovej súmernosti potom nazývame stredom súmernosti objektu. Obrázok uvádza príklady útvarov stredovo súmerných (zelené, s vyznačeným stredom súmernosti) aj tých nesúmerných (červené):
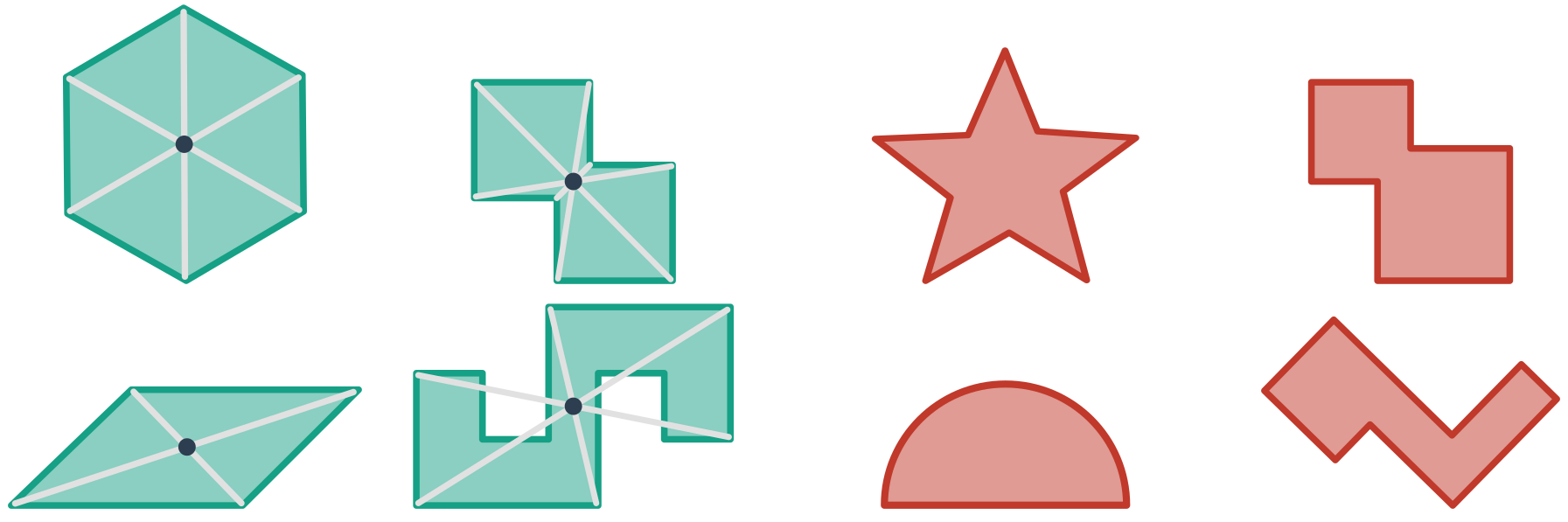
Ďalšie príklady:
Úsečka, obdĺžnik, štvorec, kosoštvorec, pravidelný šesťuholník a kruh sú stredovo súmerné.
Žiadny trojuholník nie je stredovo súmerný.
Analytická geometria
Analytická geometria nám dovoľuje zapísať geometrické problémy algebraicky a vyriešiť ich pomocou rovníc.
Najjednoduchšie objekty popísateľné analyticky sú body, úsečky a vektory v rovine alebo v priestore. Keď už dokážeme manipulovať s vektormi, môžeme ich použiť napríklad k popisu priamky alebo roviny.
V prípade priamok a rovín stále ešte ide o objekty popísateľné lineárnymi rovnicami alebo sústavami lineárnych rovníc. Ak sa začneme zaoberať aj kvadratickými rovnicami, dokážeme popísať aj kužeľosečky v rovine, napríklad kružnicu, elipsu, parabolu a hyperbolu.
Dva významné typy problémov, ktoré riešime v rámci analytickej geometrie sú polohové úlohy, v ktorých vyšetrujeme vzájomnú polohu geometrických objektov, a metrické úlohy, v ktorých počítame konkrétnu číselnú hodnotu výsledku, ako je napr. vzdialenosť dvoch bodov alebo uhol zvieraný dvomi pretínajúcimi sa priamkami.
Ak sa zaoberáme bodmi v rovine alebo v priestore, kde máme zavedenú kartézsku sústavu súradníc (v rovine s dvomi osami x,y alebo v priestore s tromi osami x,y,z), môžeme body popísať číselne súradnicami v rovine, prípadne súradnicami v priestore.
Pomocou súradníc potom dokážeme vypočítať vzdialenosť dvoch bodov „vzdušnou čiarou“ – dĺžku úsečky v rovine, prípadne v priestore.
Dĺžka úsečky v rovine
Dĺžku úsečky v rovine vypočítame rovnako ako vzdialenosť bodov v rovine.
Ak sú dané súradnice A[x_A; y_A], B[x_B; y_B], je dĺžka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}
Vzorec vychádza z Pytagorovej vety.
Je nutné počítať rozdiel súradnic v poradí „druhý bod mínus prvý“?
- Nie je. Výrazy x_B-x_A a x_A-x_B nie sú rovnaké. Ale sú opačné a vo vzorci počítame ich druhé mocniny, ktoré sa rovnajú.
- Naviac geometricky je dĺžka úsečky AB rovnaká ako dĺžka úsečky BA.
- Dôvodom zápisu práve v tomto tvare je fakt, že dĺžka úsečky je rovná veľkosti vektora \overrightarrow{AB} a pri vektore sa jeho veľkosť vždy počíta „koncový bod mínus počiatočný“.
Príklad: Dĺžka úsečky EF: E[0;-1], F[-4;2]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2}
- Dosadíme súradnice bodov E[0;-1] a F[-4;2]: \sqrt{(-4-0)^2 + (2-(-1))^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5
- Dĺžka úsečky je: |EF|=5
Dĺžka úsečky v priestore
Dĺžku úsečky v priestore vypočítame rovnako ako vzdialenosť bodov v priestore.
Ak sú dané súradnice A[x_A; y_A;z_A], B[x_B; y_B;z_B], je dĺžka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2+(z_B-z_A)^2}
Príklad: Dĺžka úsečky EF: E[-2;0;1], F[-4;2;0]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2+ (z_F-z_E)^2}
- Dosadíme súradnice bodov EF; E[-2;0;1], F[-4;2;0]:
\sqrt{(-4-(-2))^2 + (2-0)^2+(0-1)^2}=\sqrt{(-2)^2 + 2^2+(-1)^2}=\sqrt{4+4+1}=\sqrt{9}=3 - Dĺžka úsečky je: |EF|=3
Metrické úlohy
V metrických úlohách v analytickej geometrii býva úlohou vypočítať konkrétnu číselnú hodnotu veličín ako je:
- vzdialenosť dvoch objektov, napr. vzdialenosť bodu od priamky,
- odchýlka dvoch priamok v rovine.
Kužeľosečky
Ako už názov napovedá, majú kužeľosečky spoločný pôvod. Vzniknú ako rez rotačnej kuželovej plochy rovinou. 
- Kružnica vznikne rezom roviny kolmej na os kuželovej plochy.
- Ak rovinu rezu trochu nakloníme, vznikne elipsa.
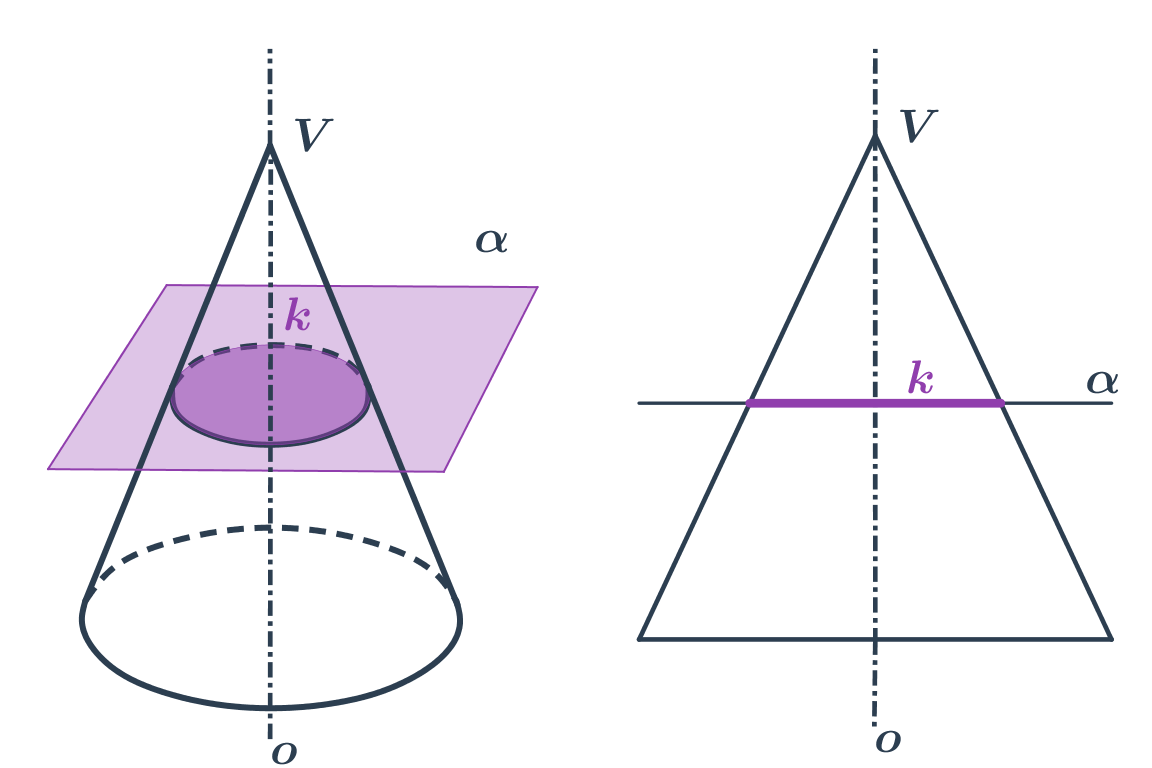
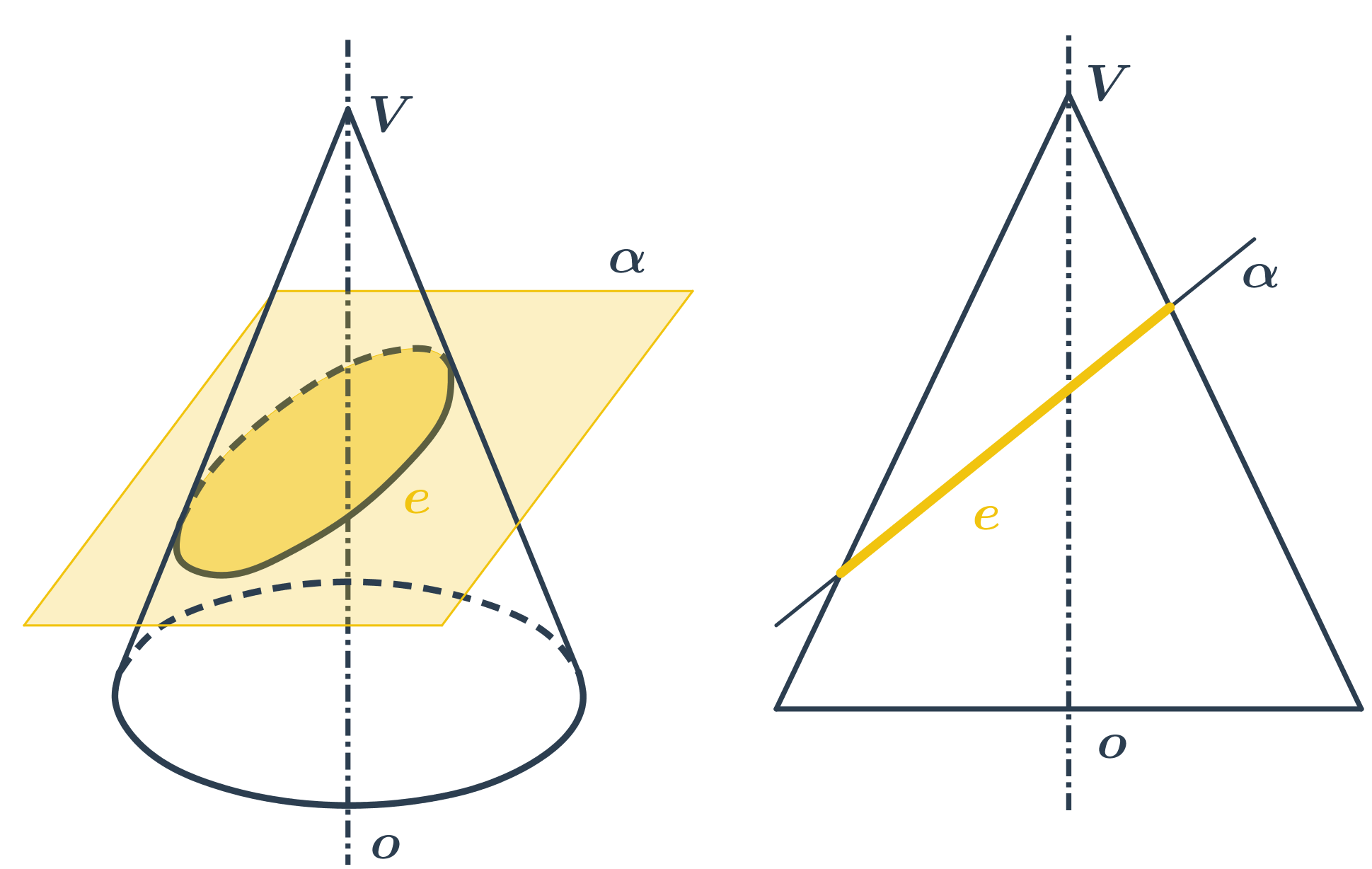
- Ak rovinu rezu nakloníme toľko, že bude rovnobežná s niektorou z priamok na kužeľovej ploche, vznikne parabola.
- Pri ďalšom nakláňaní už rovina rezu pretne obe časti kužeľovej plochy a vnikne dvojdielna hyperbola.
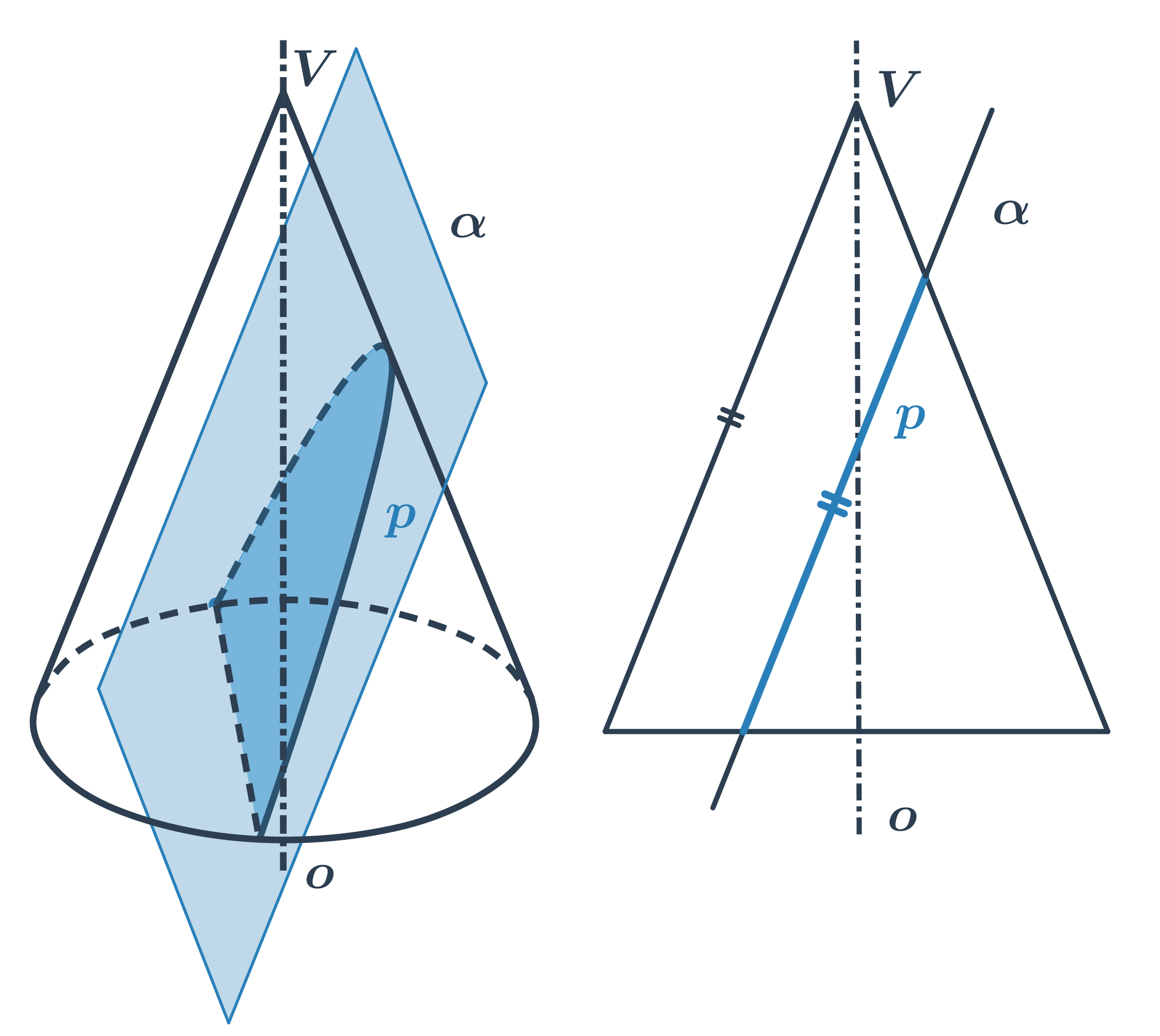
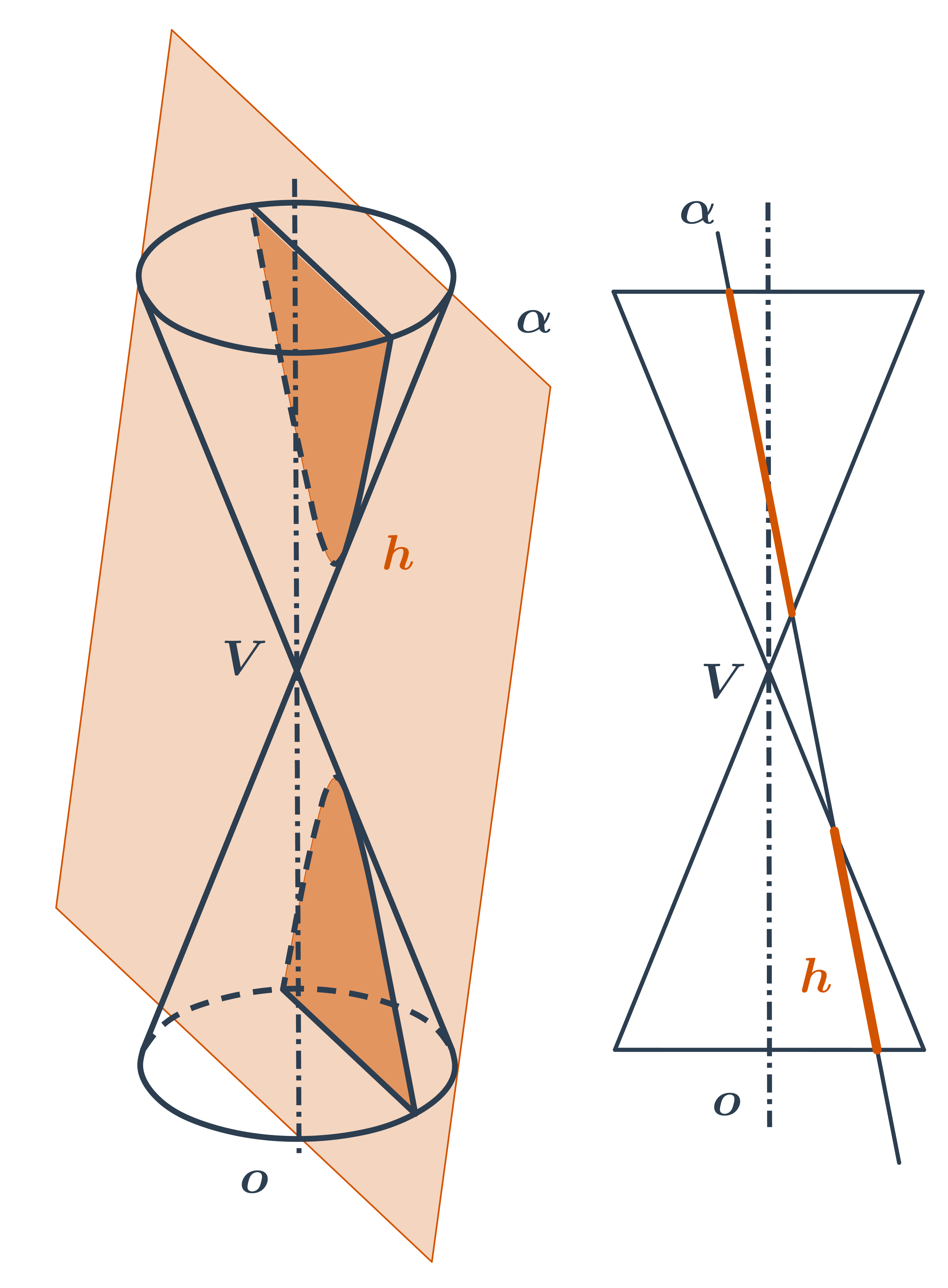
Kužeľosečky môžeme tiež chápať ako množiny bodov danej vlastnosti. V analytickej geometrii často zapisujeme tieto množiny pomocou rovníc.
Kružnica (kužeľosečka)
Kružnica je množina všetkých bodov v rovine, ktoré majú od daného pevného bodu S rovnakú vzdialenosť r. Bod S nazývame stred kružnice, hodnotu r nazveme polomer kružnice. 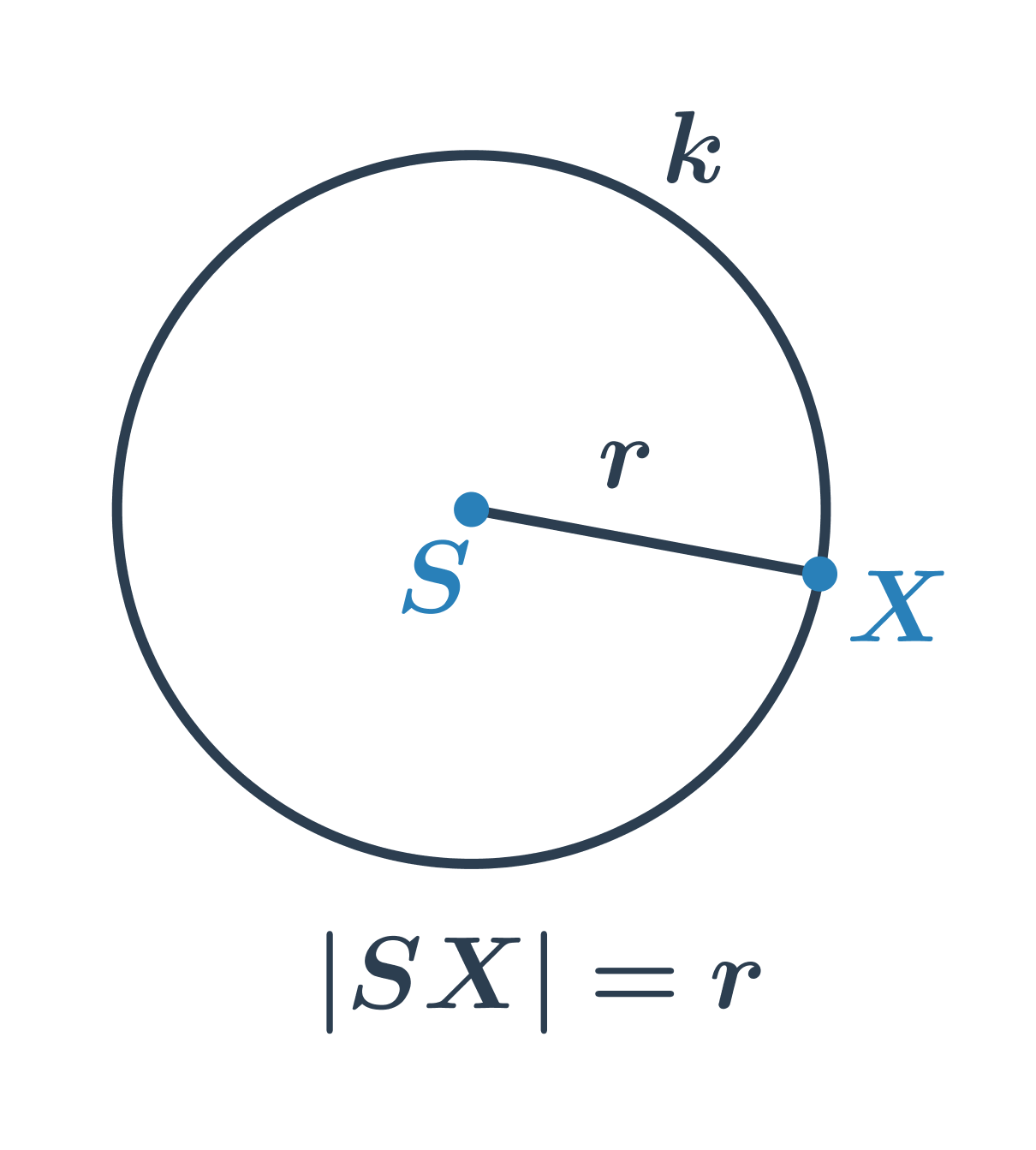
Stredová rovnica kružnice
Stredová rovnica kružnice so stredom S[m;n] a polomerom r je v tvare: (x-m)^2 +(y-n)^2=r^2 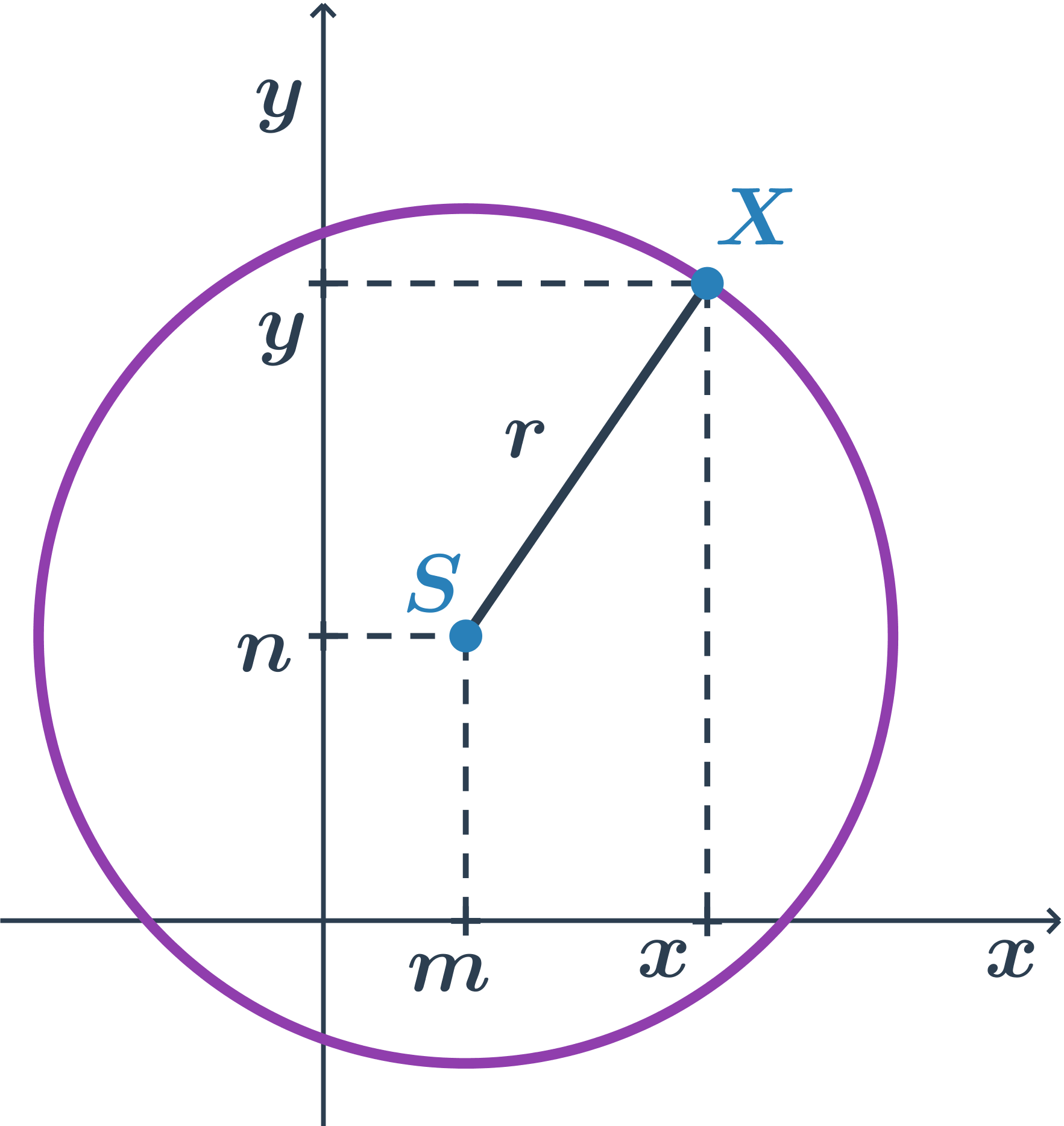
Príklad: Určite stredovú rovnicu kružnice so stredom v bode S[-1;2] a polomerom r=3.
- Stredová rovnica je v tvare: (x-m)^2 +(y-n)^2=r^2
- Dosadíme súradnice stredu a polomer. Pri dosadení si dáme pozor na to, že súradnice stredu v stredovej rovnici odčítame: (x-(-1))^2 +(y-2)^2=3^2
- Po úprave: (x+1)^2 +(y-2)^2=9
Všeobecná rovnica kružnice
Podobne ako existuje niekoľko tvarov rovníc priamky, môžeme aj rovnicu kružnice zapísať rôznymi spôsobmi. Všeobecná rovnica kružnice je v tvare: x^2 +y^2-2mx-2ny+p=1.
Každá rovnica v tomto tvare ale nemusí ešte byť všeobecnou rovnicou kružnice. Pre všeobecnú rovnicu kružnice musí platiť, že výraz m^2+n^2-p je kladný. Praktické overenie, či ide o kružnicu, ale väčšinou vykonávame prevedením na stredovú rovnicu kružnice.
Príklad: Nájdite stred a polomer kružnice danej všeobecnou rovnicou x^2+y^2+4x+6y-12=0.
- Najskôr si usporiadame členy podľa premenných: x^2+4x+y^2-6y-12=0.
- Našim ďalším cieľom je upraviť výraz na ľavej strane ako súčet dvoch druhých mocnín (štvorcov), podľa vzorcov a^2\pm 2ab+b^2=(a\pm b)^2.
- K obom stranám rovnice pripočítame konštanty 4 a 9, aby sme súčty členov s premennými x a y mohli upraviť na druhé mocniny (prevedieme v oboch prípadoch doplnenie na štvorec): x^2+4x+4+y^2-6y+9-12=4+9
- A upravíme: (x+2)^2 +(y-3)^2-12=13
- Na záver ešte prevedieme -12 na druhú stranu rovnice: (x+2)^2 +(y-3)^2=25
- Týmto sme previedli všeobecnú rovnicu kružnice na stredovú rovnicu kružnice.
- Polomer kružnice je r=\sqrt{25}=5.
- Súradnice stredu S[m,n] odčítame v stredovej rovnici od premenných x a y, majú teda opačné znamienka než konštanty v zátvorkách v stredovej rovnici \Rightarrow S[-2;3].
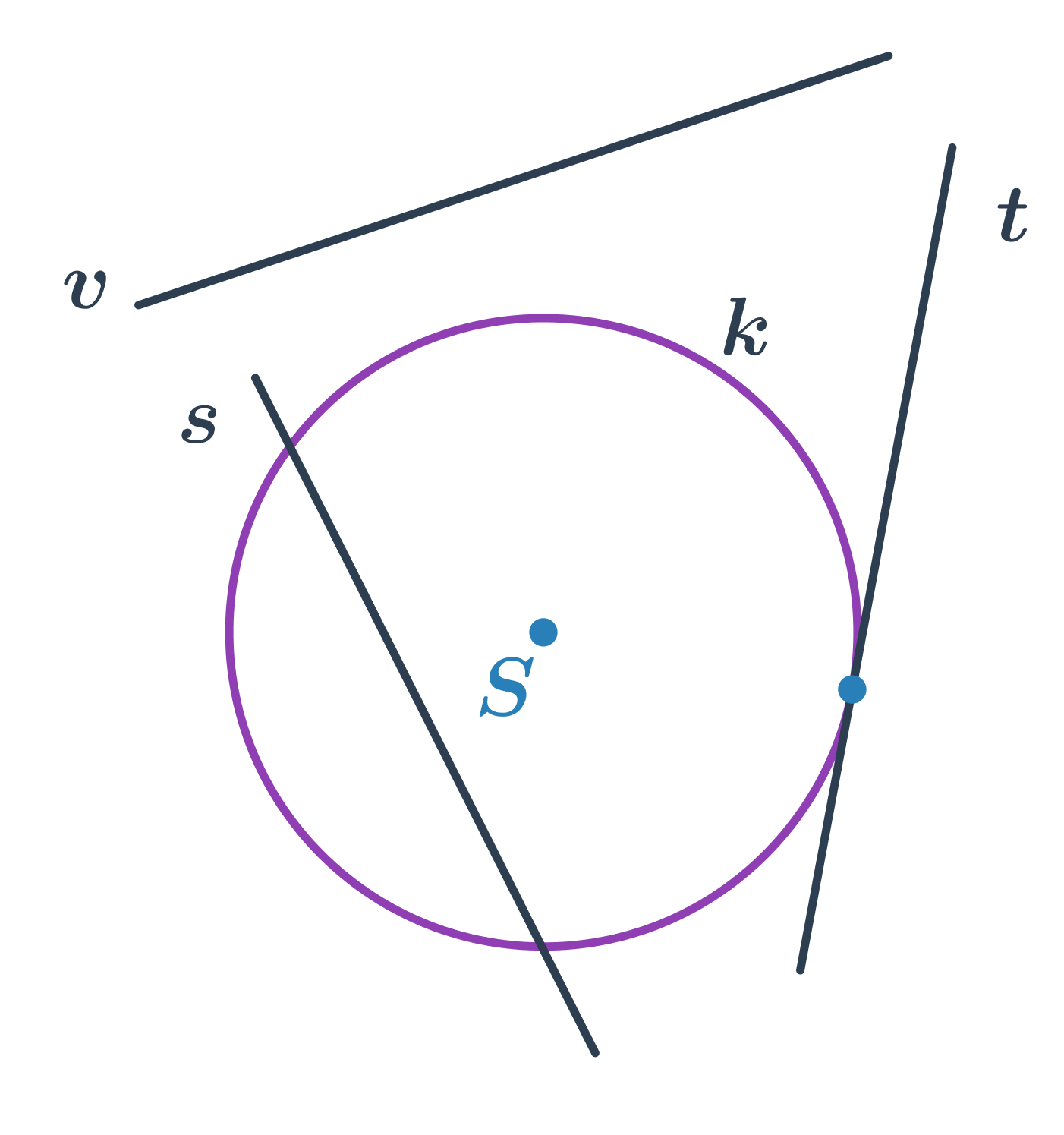
Kružnica a priamka
- priamka s pretína kružnicu v dvoch bodoch – sečnica kružnice
- priamka t pretína kružnicu v jednom bode – dotyčnica kružnice
- priamka v kružnici nepretína – vonkajšia priamka kružnice
Rovnice dotyčnice kružnice v bode, ktorý leží na kružnici
Kružnica daná rovnicou (x-m)^2 +(y-n)^2=r^2 má v bode T[x_0;y_0] dotyčnicu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2.Ako si zapamätať rovnicu dotyčnice
- Stredová rovnica je v tvare (x-m)^2 +(y-n)^2=r^2.
- Zátvorky rozložíme na súčiny dvojčlenov (x-m)(x-m) +(y-n)(y-n)=r^2.
- V každom súčine zameníme jedno x za x_0 a jedno y za y_0
- Dostaneme rovnicu dotyčnice (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
Príklad: Určite rovnicu dotyčnice kružnice (x-1)^2+(y+2)^2=13 v jej bode T[3;1].
- Overíme, či bod T leží na kružnici: (3-1)^2+(1+2)^2=13 \Rightarrow 4+9=13
- Dotyčnica má rovnicu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
- Dosadíme súradnice bodu T: (3-1)(x-1) +(1+2)(y+2)=13
- Roznásobíme zátvorky: 2x-2 +3y+6=13
- A dostaneme všeobecnú rovnicu dotyčnice 2x+3y-9=0
Polára kružnice
Z bodu R mimo kružnicu môžeme zostrojiť dve dotyčnice k danej kružnici. Priamka určená bodmi dotyku dotyčníc sa nazýva polára kružnice vzhľadom k bodu R. 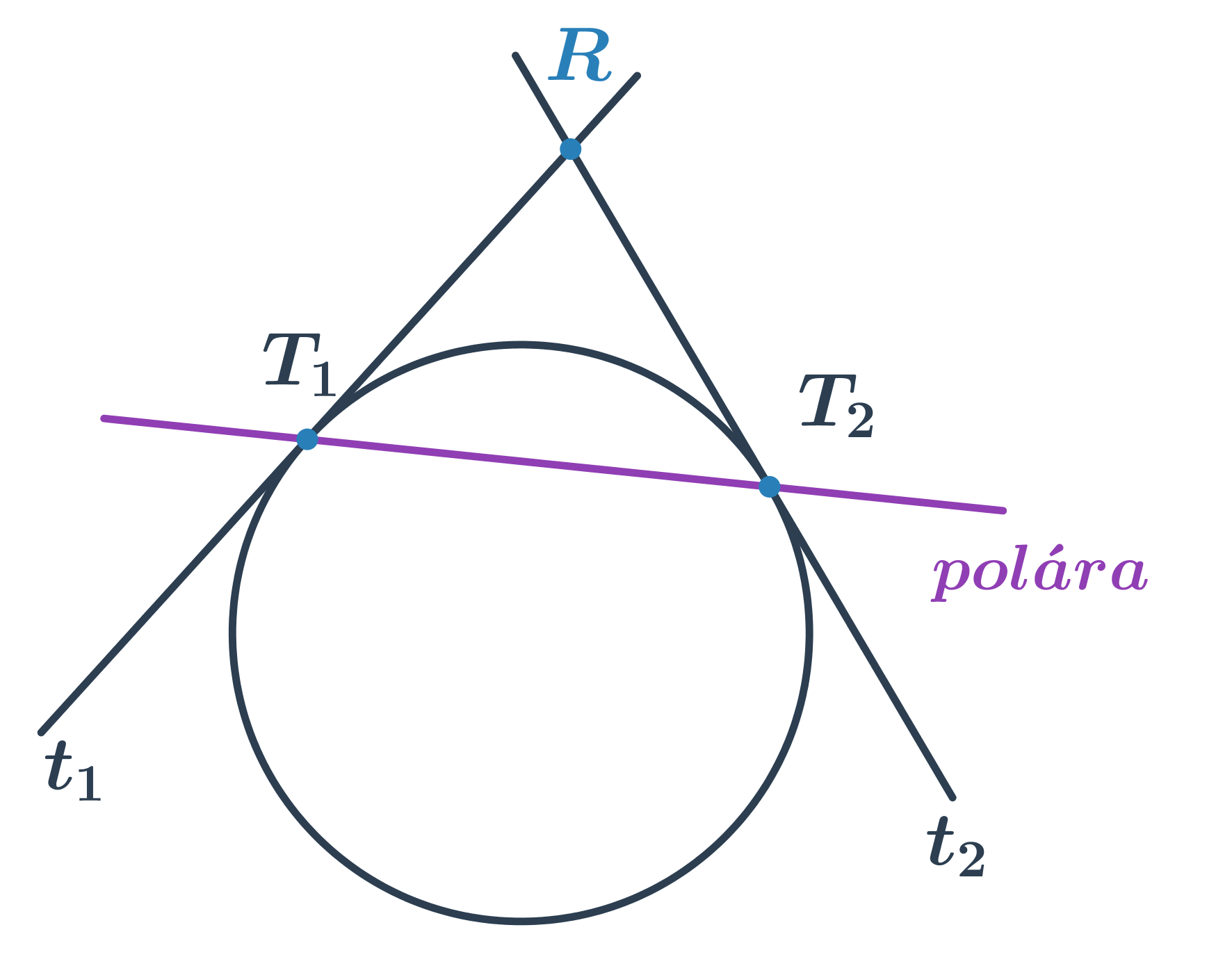
Rovnica poláry kružnice (x-m)^2 +(y-n)^2=r^2 vzhľadom k bodu R[r_1;r_2] je (r_1-m)(x-m) +(r_2-n)(y-n)=r^2.
Na čo poláru použijeme?
- Poláru využívame na konštrukciu dotyčníc ležiacich z bodu mimo kružnicu.
- Podľa vzorca určíme rovnicu poláry, teda priamky.
- Nájdeme priesečníky poláry a kružnice – to sú body dotyku hľadaných dotyčníc.
- Keď poznáme body dotyku, určíme podľa vzťahu pre rovnicu dotyčnice v bode kružnice všeobecné rovnice oboch dotyčníc.
Elipsa je množina všetkých bodov v rovine, ktoré majú od dvoch rôznych bodov (ohnísk) stály súčet vzdialeností 2a, ktorý je väčší než vzdialenosť ohnísk.
Stredová rovnica elipsy
Tvar stredovej rovnice elipsy so stredom S[m;n] s veľkosťami hlavnej a vedľajšej polosi a a b závisí od polohy hlavnej osi:
hlavná os je rovnobežná s osou x, rovnica je v tvare: \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1
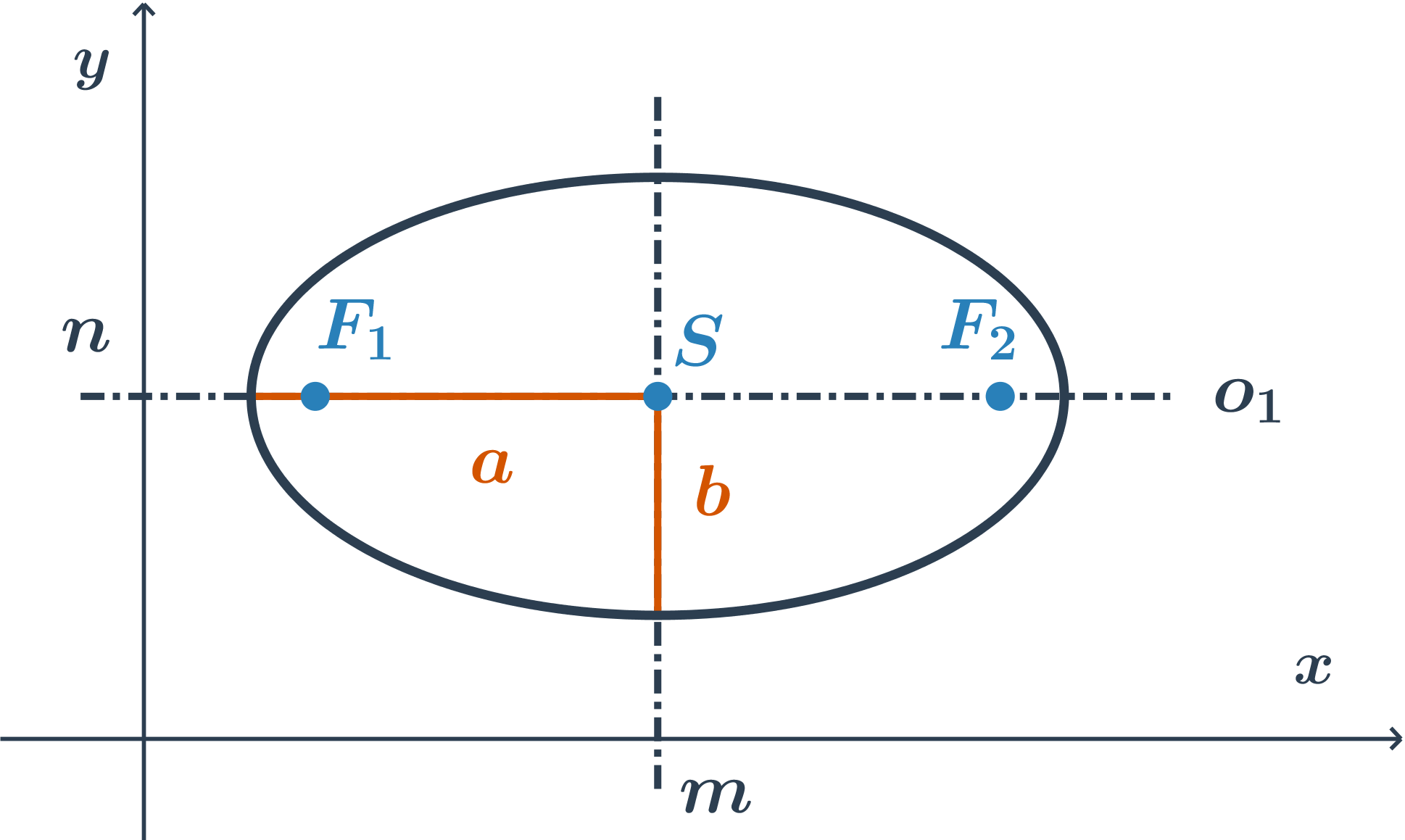
hlavná os je rovnobežná s osou y, rovnica je v tvare: \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1
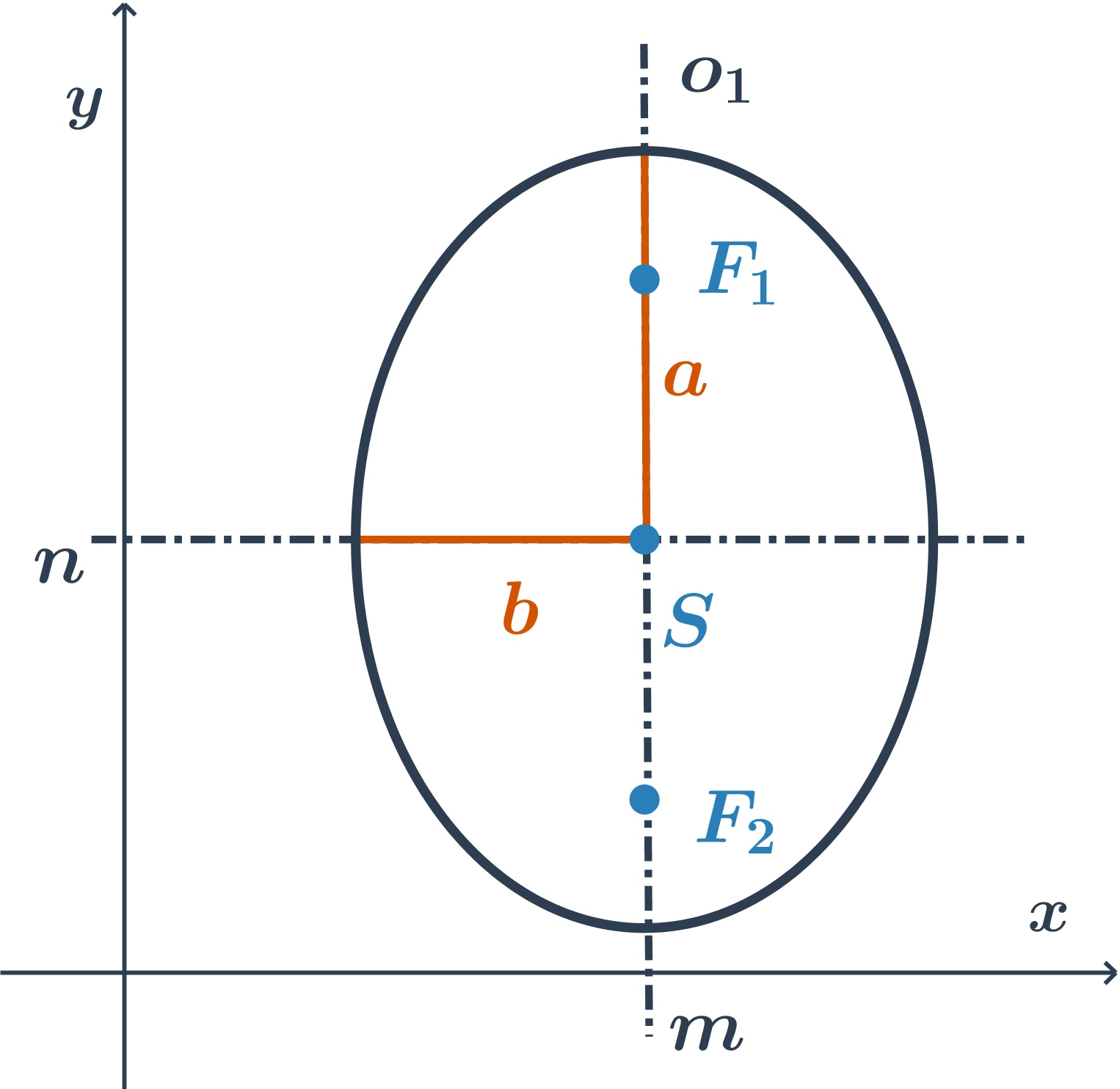
Návod: ako z rovnice zistiť, s ktorou súradnicovou osou je rovnobežná hlavná os elipsy
- Pozrieme sa do menovateľov.
- Väčší menovateľ je druhá mocnina veľkosti hlavnej polosi (a menší menovateľ je druhá mocnina veľkosti vedľajšej polosi).
- Premenná v danom čitateli (zlomku s väčším menovateľom) potom určuje, s ktorou osou je hlavná os elipsy rovnobežná.
- Stručne povedané: ak je väčšie číslo napríklad v menovateli s premennou x, je hlavná os rovnobežná s osou x.
Príklad: určenie stredovej rovnice elipsy s daným stredom, veľkosťami polôs a smerom hlavnej osi
Určite stredovú rovnicu elipsy so stredom v bode S[-2;3], je‑li a=3, b=2 ak hlavná os je rovnobežná s osou y.
- Stredová rovnica je v tvare \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1.
- Dosadíme súradnice stredu a veľkosti hlavnej a vedľajšej polosi. Pri dosadení si dáme pozor na to, že súradnice stredu odčítame: \frac{(x-(-2))^2}{2^2} +\frac{(y-3)^2}{3^2}=1
- Po úprave: \frac{(x+2)^2}{4} +\frac{(y-3)^2}{9}=1
Všeobecná rovnica elipsy
Podobne ako existuje niekoľko rovníc priamky, môžeme aj rovnicu elipsy zapísať iným spôsobom. Všeobecná rovnica elipsy je v tvare:
Ax^2 +By^2+Cx+Dy+E=1, A\ne B, A\cdot B>0.
Každá rovnica v tomto tvare ale nemusí byť všeobecnou rovnicou elipsy. Praktické overenie, či ide o elipsu vykonávame prevedením na stredovú rovnicu.
Príklad: určuje daná rovnica elipsu?
Rozhodnite, či rovnica x^2+3y^2+8x-18y+31=0 určuje elipsu.
- Najskôr si usporiadame členy: x^2+8x+3y^2-18y+31=0.
- Z členov s premennou y vytkneme 3: x^2+8x+3(y^2-6y)+31=0
- K obom stranám rovnice pripočítame konštanty 16 a 27, aby sme členy s premennými x a y mohli upraviť podľa vzťahu (a\pm b)^2=a^2 \pm 2ab +b^2.
- Máme: x^2+8x+16+3(y^2-6y+9)+31=16+27
- A upravíme: (x+4)^2 +3(y-3)^2+31=43
- Prevedieme konštantu 31 na druhú stranu rovnice: (x+4)^2 +3(y-3)^2=12
- Na záver rovnicu vydelíme 12: \frac{(x+4)^2}{12} +\frac{(y-3)^2}{4}=1
- Ide teda o elipsu.
Elipsa a priamka
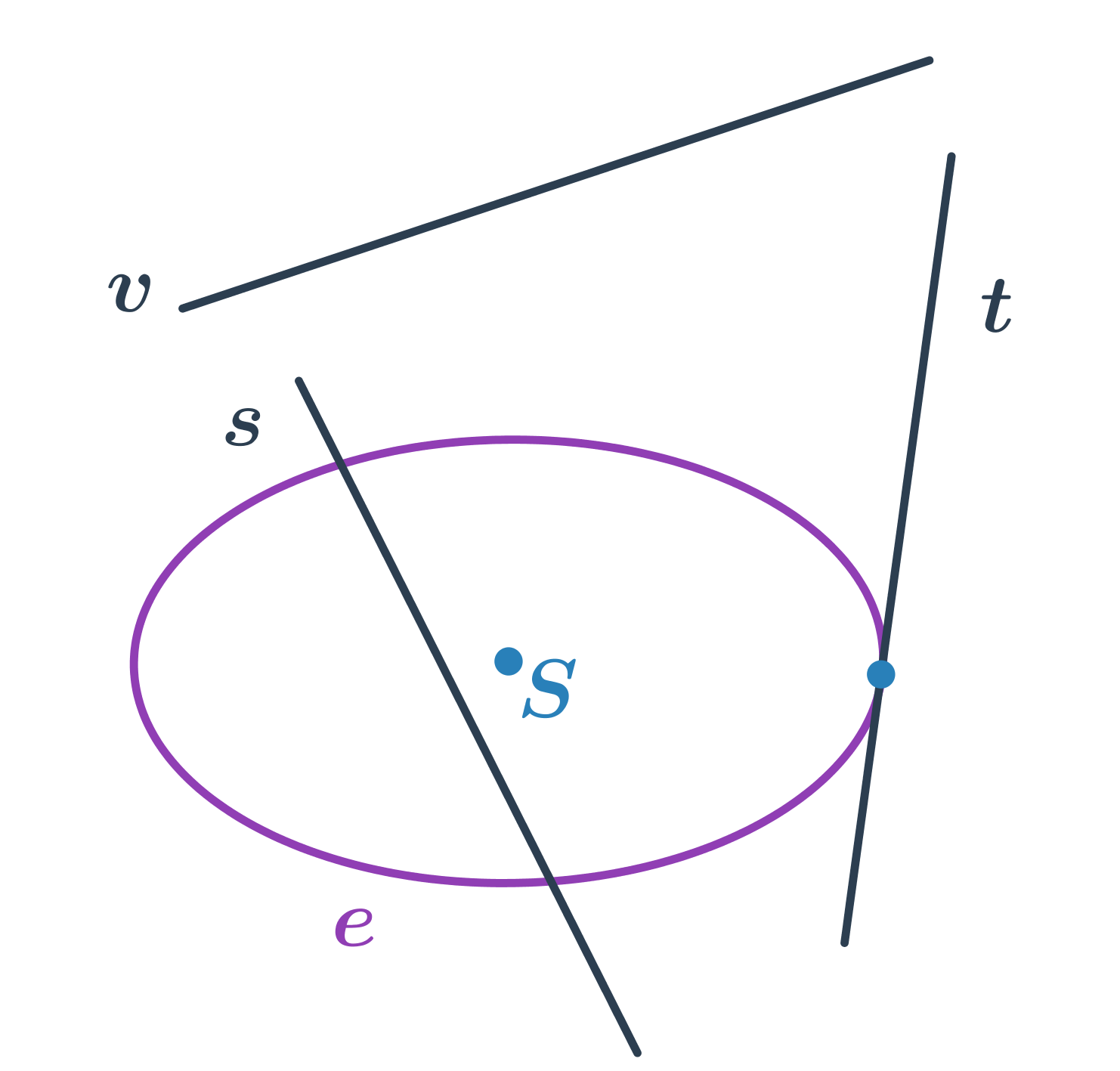
- priamka s pretína elipsu v dvoch bodoch – sečnica elipsy
- priamka t pretína elipsu v jednom bode – dotyčnica elipsy
- priamka v elipsu nepretína – vonkajšia priamka elipsy
Rovnice dotyčnice elipsy v bode, ktorý leží na elipse
Elipsa daná rovnicou \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1 má v bode T[x_0;y_0] dotyčnicu určenú rovnicou:
\frac{(x-m)(x_0-m)}{a^2} +\frac{(y-n)(y_0-n)}{b^2}=1
Podobne môžeme zapísať aj rovnicu dotyčnice elipsy, ktorá má hlavnú os rovnobežnú s osou y.
Príklad: určenie rovnice dotyčnice elipsy v jej danom bode
Určite rovnicu dotyčnice elipsy \frac{(x-2)^2}{9} +\frac{(y-2)^2}{18}=1 v jej bode T[1;-2].
- Overíme, či bod T leží na elipse: \frac{(1-2)^2}{9} +\frac{(-2-2)^2}{18}=1 \Rightarrow \frac19+\frac{16}{18}=1 \Rightarrow 1=1
- Dotyčnica má rovnicu \frac{(x-m)(x_0-m)}{b^2} +\frac{(y-n)(y_0-n)}{a^2}=1
- Dosadíme súradnice bodu T: \frac{(x-2)(1-2)}{9} +\frac{(y-2)(-2-2)}{18}=1
- Zbavíme sa zlomkov: 2(x-2)\cdot(-1) +(y-2)\cdot(-4)=18
- Roznásobíme zátvorky: -2x+4 -4y+8=18
- A dostaneme všeobecnú rovnicu dotyčnice: x+2y+3=0
Hyperbola
Hyperbola je množina všetkých bodov v rovine, ktoré majú od dvoch rôznych bodov (ohnísk) stály rozdiel vzdialeností 2a, ktorý je menší než vzdialenosť ohnísk. Hyperbola sa skladá z dvoch častí – vetiev hyperboly. Tieto dve vetvy sa blížia k priamkam, ktoré nazývame asymptoty.
Stredová rovnica hyperboly
Tvar stredovej rovnice hyperboly so stredom S[m;n] s veľkosťami hlavnej a vedľajšej polosi a,b závisí od polohy hlavnej osi.
Stredová rovnica hyperboly s hlavnou osou rovnobežnou s osou x
Ak je hlavná os rovnobežná s osou x, rovnica je v tvare \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1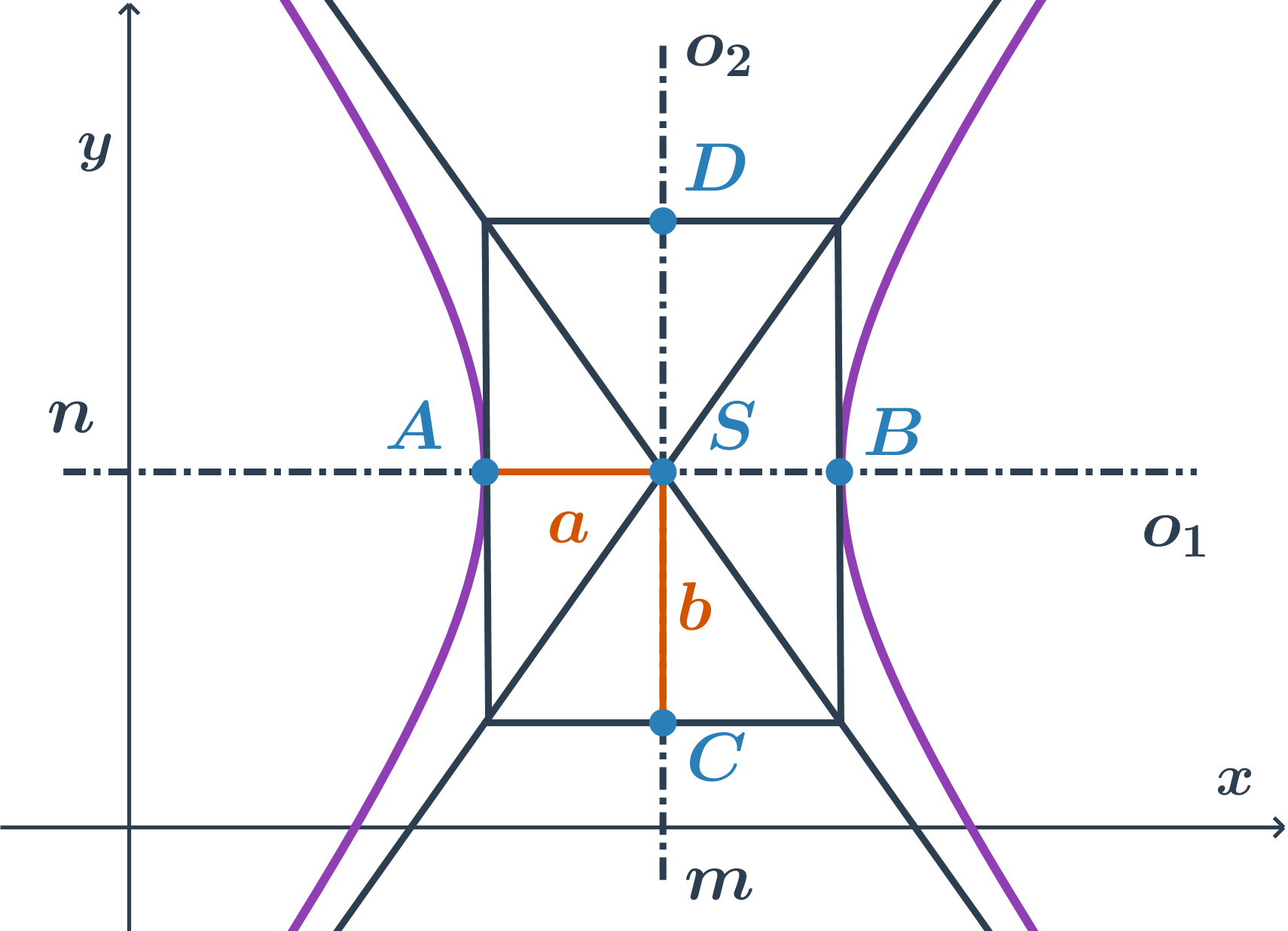
Stredová rovnica hyperboly s hlavnou osou rovnobežnou s osou y
Ak je hlavná os rovnobežná s osou y, rovnica je v tvare -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1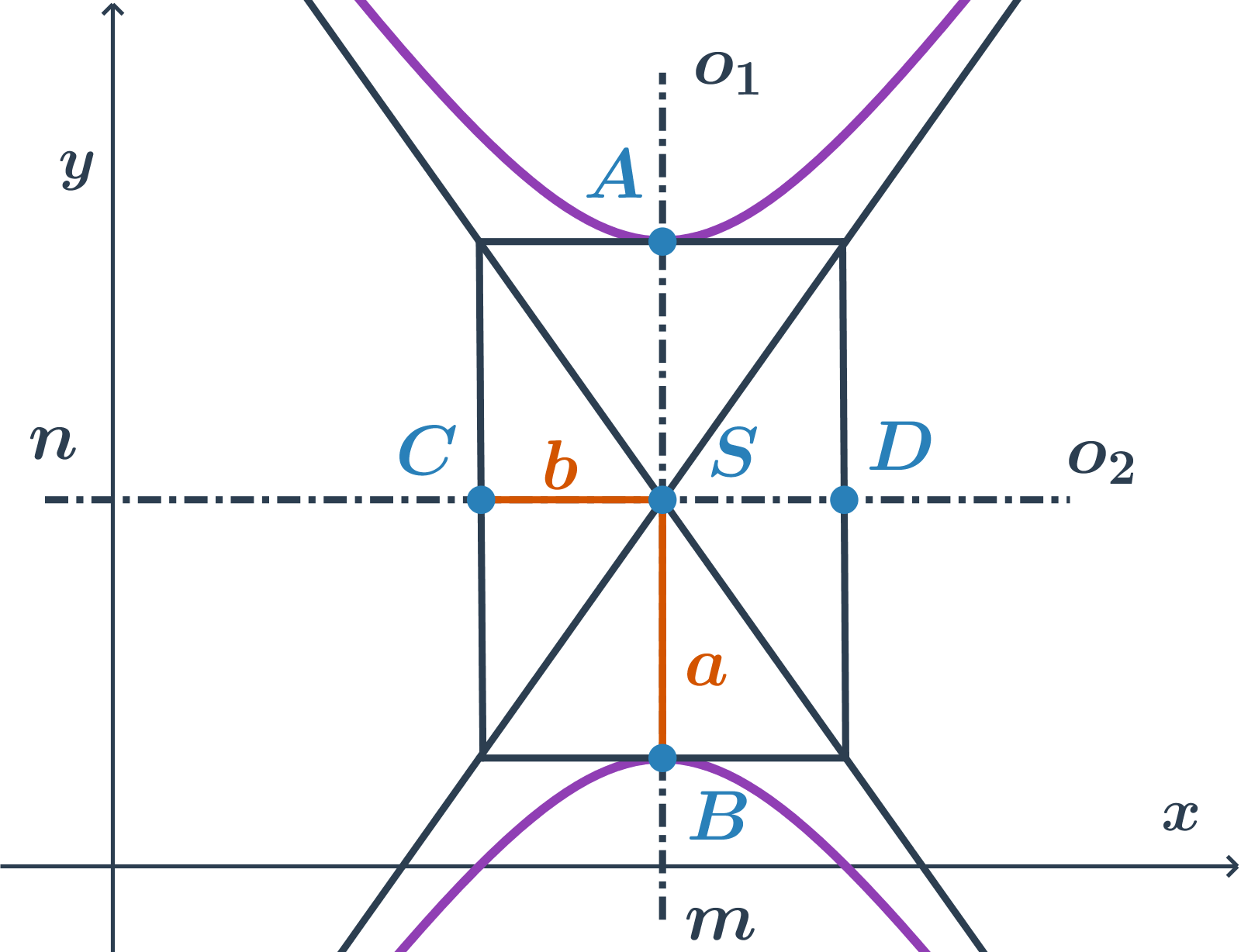
Oproti elipse, nemusí byť v prípade hyperboly vždy hlavná polos a dlhšia než vedľajšia polos b. Pre rovnoosú hyperbolu dokonca platí a=b.
Ako zo stredovej rovnice poznáme, s ktorou súradnicovou osou je rovnobežná hlavná os hyperboly?
- Pozrieme sa na znamienka členov s premennou x a y.
- Premenná v člene, ktorý má pred sebou znamienko plus udáva, s ktorou súradnicovou osou je rovnobežná hlavná os hyperboly.
- V menovateli danej premennej je potom (v druhej mocnine) veľkosť hlavnej polosi.
- Stručne povedané: ak je znamienko plus napríklad v prípade člena s premennou x, je hlavná os rovnobežná s osou x a v menovateli je druhá mocnina veľkosti hlavnej polosi a.
Príklad: Určenie stredovej rovnice hyperboly
Určite stredovú rovnicu hyperboly so stredom v bode S[1;-5], ak je veľkosť hlavnej polosi 2, veľkosť vedľajšej polosi 6 a hlavná os je rovnobežná s osou y.
- Stredová rovnica je v tvare -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1. Hlavná polos má veľkosť a, vedľajšia b.
- Dosadíme súradnice stredu a veľkosti hlavnej a vedľajšej polosi. Pri dosadení si dáme pozor na to, že súradnice stredu odčítame: -\frac{(x-1)^2}{6^2} +\frac{(y-(-5))^2}{2^2}=1
- Po úprave: -\frac{(x-1)^2}{36} +\frac{(y+5)^2}{4}=1
Rovnice asymptot
Už vieme, že asymptoty sú priamky, ku ktorým sa hyperbola blíži. Pomôžu pri vykreslení hyperboly. Rovnica asymptot závisí od tvaru stredovej rovnice hyperboly.
Pre hyperbolu danú rovnicou v tvare \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 sú rovnice asymptot:
y=\pm\frac{b}{a}(x-m)+n
Pre hyperbolu danú rovnicou v tvare -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1 sú rovnice asymptot:
y=\pm\frac{a}{b}(x-m)+n
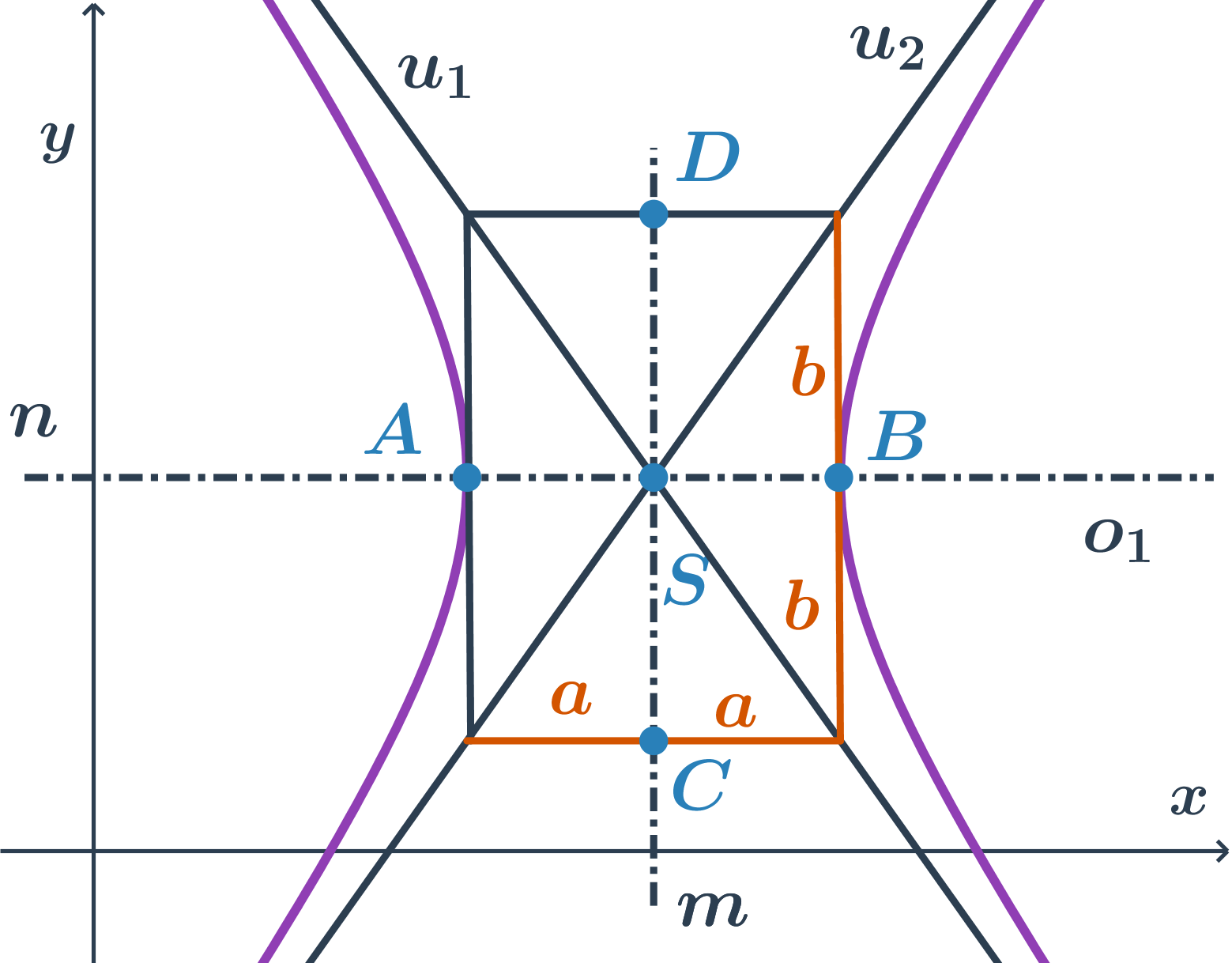
Ako načrtnúť hyperbolu?
- Najskôr si vyznačíme stred, hlavné a vedľajšie vrcholy.
- Potom zostrojíme charakteristický obdĺžnik hyperboly. To je obdĺžnik, ktorý má strany rovnobežné s osami a vrcholmi hyperboly sú stredy jeho strán. Dĺžky jeho strán sú teda 2a a 2b.
- Asymptoty sú uhlopriečky charakteristického obdĺžnika.
Všeobecná rovnica hyperboly
Podobne ako existuje niekoľko rovníc elipsy, môžeme aj rovnicu hyperboly zapísať rôznymi spôsobmi. Všeobecná rovnica hyperboly je v tvare: Ax^2 +By^2+Cx+Dy+E=1, A\cdot B<0. Podmienka A\cdot B<0 zaručuje, že konštanty A, B majú opačné znamienka. Každá rovnica v tomto tvare ale nemusí byť všeobecnou rovnicou hyperboly. Praktické overenie, či ide o hyperbolu vykonávame prevedením na stredovú rovnicu.
Príklad: Určuje daná rovnica hyperbolu?
Rozhodnite, či rovnica -x^2+2y^2+8x-18y+31=0 určuje hyperbolu.
- Najskôr si usporiadame členy: -x^2+8x+y^2-18y+40=0.
- Z členov s premennou x vytkneme -1: -(x^2-8x)+y^2-18y+40=0
- K obom stranám rovnice pripočítame konštantu 81 a odčítame konštantu 16, aby sme členy s premennými x a y mohli upraviť podľa vzťahu pre (a\pm b)^2: -(x^2-8x+16)+y^2-18y+81+40=81-16
- A upravíme: -(x-4)^2 +(y-9)^2+40=65
- Prevedieme konštantu 40 na druhú stranu rovnice: -(x-4)^2 +(y-9)^2 =25
- Na záver rovnice vydelíme 25: -\frac{(x-4)^2}{25} +\frac{(y-9)^2}{25}=1
- Ide teda o hyperbolu. Hlavná os je rovnobežná s osou y a a=b=5.
Hyperbola a priamka
- priamka s pretína hyperbolu v dvoch bodoch – sečnica hyperboly
- priamka t pretína hyperbolu v jednom bode – dotyčnica hyperboly
- priamka v hyperbolu nepretína – vonkajšia priamka hyperboly
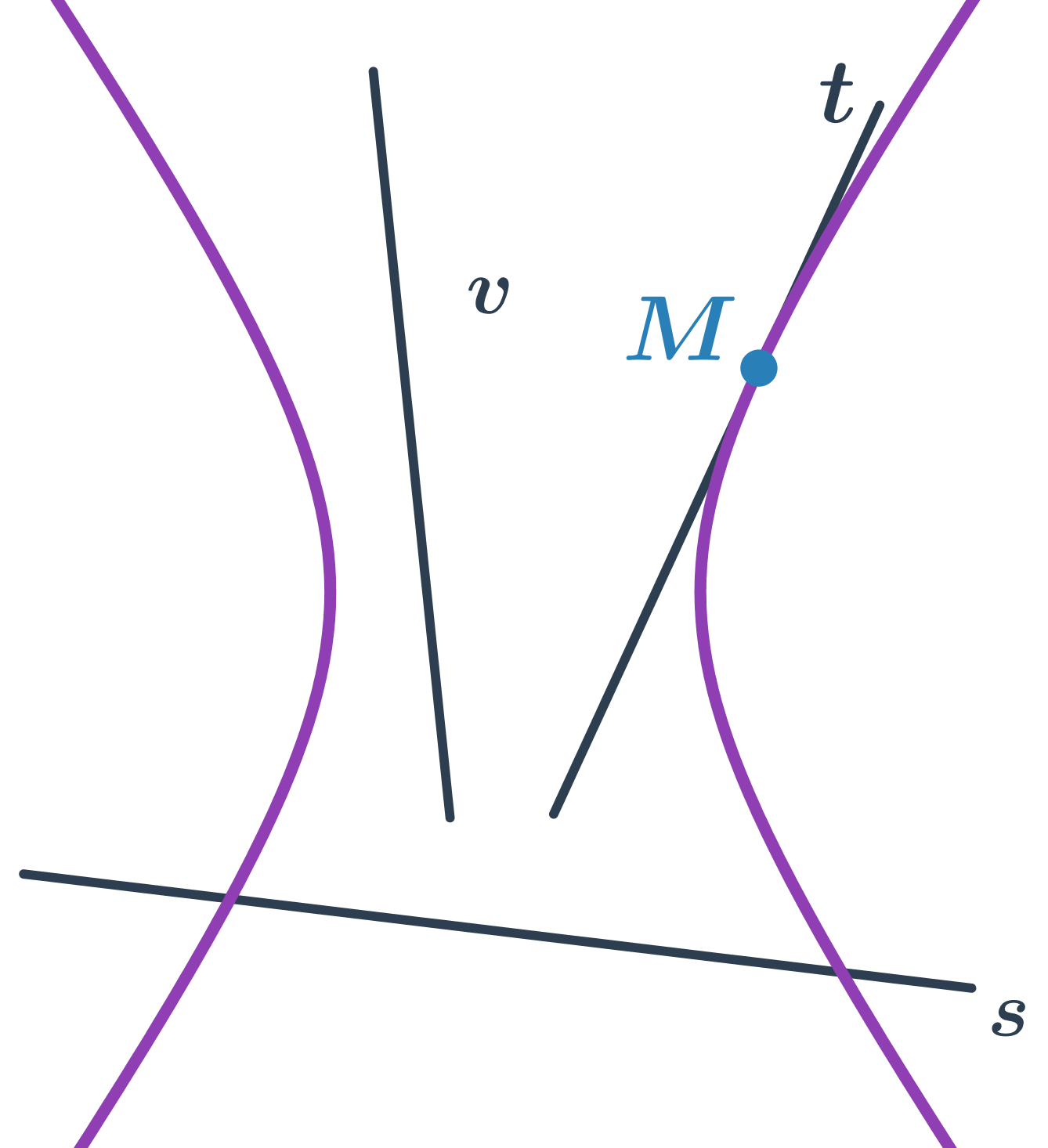
Špeciálnou polohou sečnice hyperboly je priamka, ktorá je rovnobežná s asymptotou. Taká sečnica potom pretína hyperbolu v jednom bode. 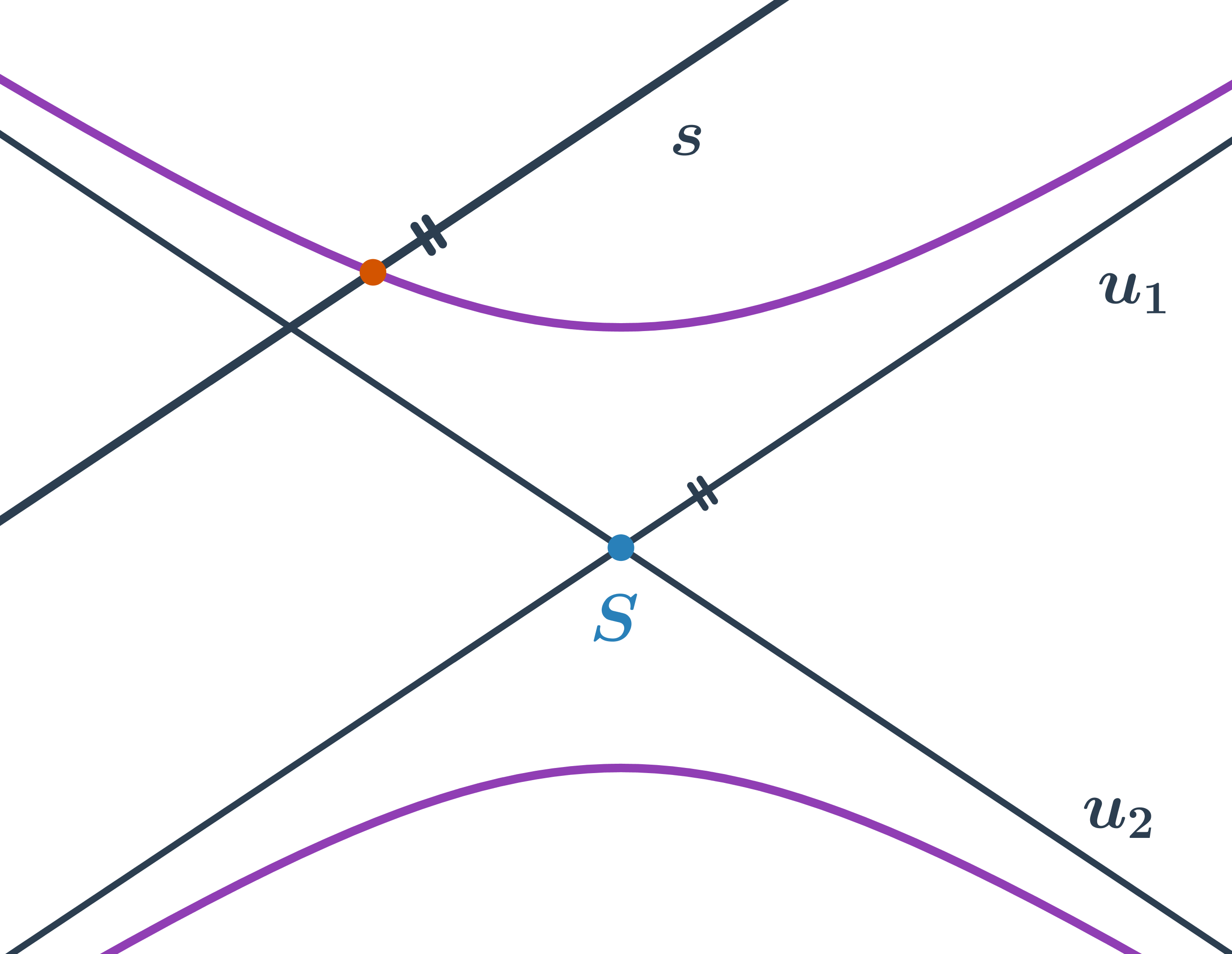
Ako rozlíšiť, či je priamka dotyčnica alebo sečnica?
- Najskôr určíme vzájomnú polohu priamky a hyperboly.
- Ak vyjdú dva priesečníky, ide o sečnicu vo všeobecnej polohe.
- Ak vyjde jeden priesečník, musíme ešte rozhodnúť, či je priamka rovnobežná s asymptotou. Ak nie, ide o dotyčnicu. V opačnom prípade ide o sečnicu.
Rovnica dotyčnice hyperboly v bode, ktorý leží na hyperbole
Hyperbola daná rovnicou \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 má v bode T[x_0;y_0] dotyčnicu danú rovnicou:
\frac{(x-m)(x_0-m)}{a^2} -\frac{(y-n)(y_0-n)}{b^2}=1.
Podobne môžeme zapísať aj rovnicu dotyčnice hyperboly, ktorá má hlavnú os rovnobežnú s osou y.


 Slovenčina
Slovenčina Angličtina
Angličtina Informatika
Informatika Vieme to
Vieme to Nemčina
Nemčina Biológia
Biológia Zemepis
Zemepis Chémia
Chémia
