Funkcia f je lineárna, ak ju je možné vyjadriť v tvare f(x) = a\cdot x + b, kde a a b sú konštanty. Grafom lineárnej funkcie je priamka. Parameter a je smernica (tiež nazývaná sklon), parameter b určuje jej zvislý posun (tiež nazývaný absolútny člen).
Príklady lineárnych funkcií:
- f(x) = 2x
- f(x) = -4x+8
- f(x) = \frac13 x + 1{,2}
Aby bola funkcia lineárna, nemusí byť nutne priamo zapísaná v tvare f(x) = a\cdot x + b. Stačí, keď ide na tento tvar upraviť. Príklady:
- f(x) = 2-x môžeme prepísať ako f(x)= -1x + 2, čo je lineárna funkcia so smernicou -1 a absolútnym členom 2.
- f(x) = 5(3-x) môžeme prepísať ako f(x)= -5x + 15, čo je lineárna funkcia so smernicou -5 a absolútnym členom 15.
- f(x) = x^2 + 7 - x(x-1) vyzerá na prvý pohľad ako kvadratická funkcia, ale môžeme ju upraviť na f(x)= x + 7 (kvadratický člen sa vyruší), takže ide o lineárnu funkciu.
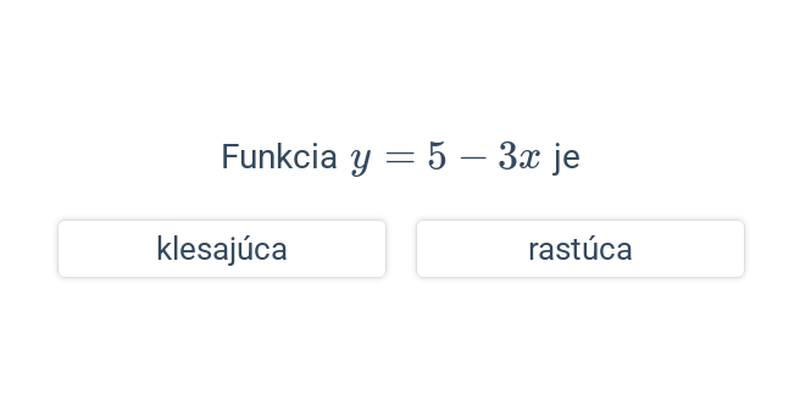
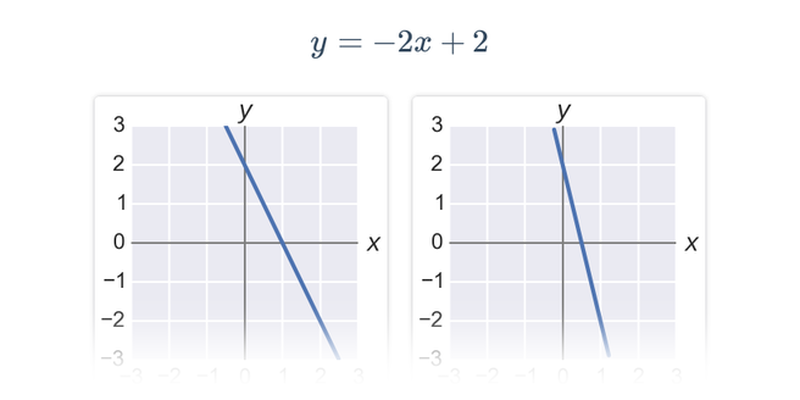
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.