







Výborne, je dosiahnutý %% štít
Priamky » Počítanie »
Priamky
Počítanie
QR kód
Kód / krátka adresa
Skopírujte kliknutím. Skopírované!
viemeto.eu/GNM
Vzájomná poloha priamok v rovine
Vzájomnú polohu dvoch priamok môžeme ľahko určiť, ak poznáme súradnice ich smerových, prípadne normálových vektorov. Rovnobežne priamky majú rovnaký smer, teda ich smerové vektory sú kolineárne. Normálové vektory dvoch rovnobežných priamok sú tiež kolineárne. V špeciálnom prípade môžu byť priamky totožné. Rôznobežné priamky majú jeden spoločný bod, tento bod musí spĺňať rovnice oboch priamok. Ich smerové vektory nie sú kolineárne, normálové vektory tiež nie sú kolineárne.
Rovnobežky zadané parametrickými rovnicami
Určite vzájomnú polohu dvoch priamok p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-3+3t\\y&=&\hspace{0.25cm}2+t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&1-3s\\y&=&2-s\\&&s\in\mathbb{R}\end{array}
- smerový vektor priamky p:\hspace{0.25cm}\vec{u}=(3;1)
- smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(-3;-1)
- Priamky p a q sú rovnobežné, pretože ich smerové vektory sú kolineárne.
- Overíme, že priamky nie sú totožné. Stačí určiť, či bod, ktorý leží na jednej priamke neleží na priamke druhej.
- Na priamke p leží napríklad bod A=[-3;2].
- Overíme, že tento bod neleží na priamke q dosadením súradníc bodu A do rovníc priamky q: \begin{array}{rrl}-3&=&1-3s \Rightarrow s=\frac{4}{3}\\2&=&2-\hspace{0.15cm}s\Rightarrow s=0\end{array}
- Vyšli rôzne hodnoty parametra s, takže bod A neleží na q \Rightarrow priamky nie sú totožné
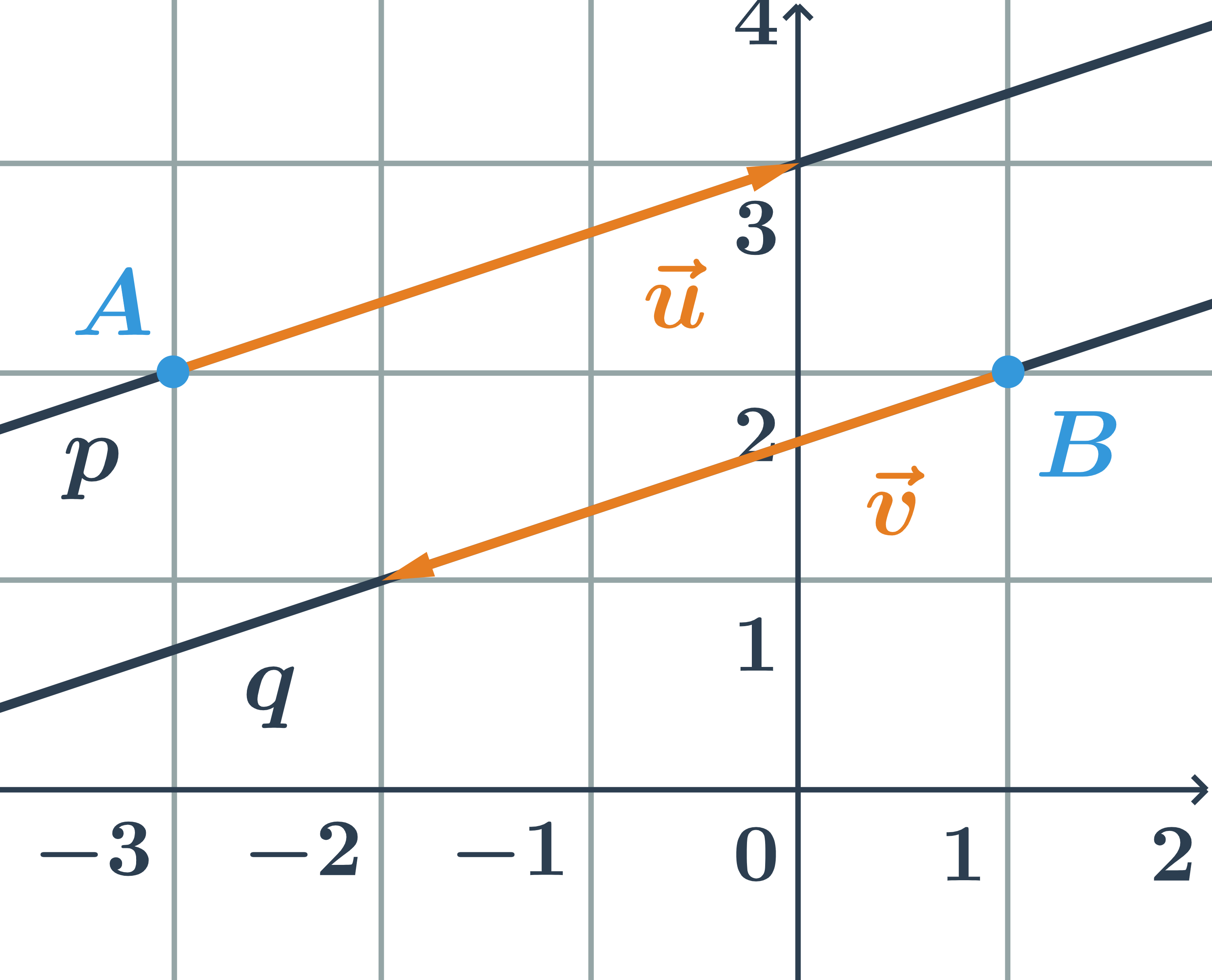
Rovnobežky zadané všeobecnými rovnicami
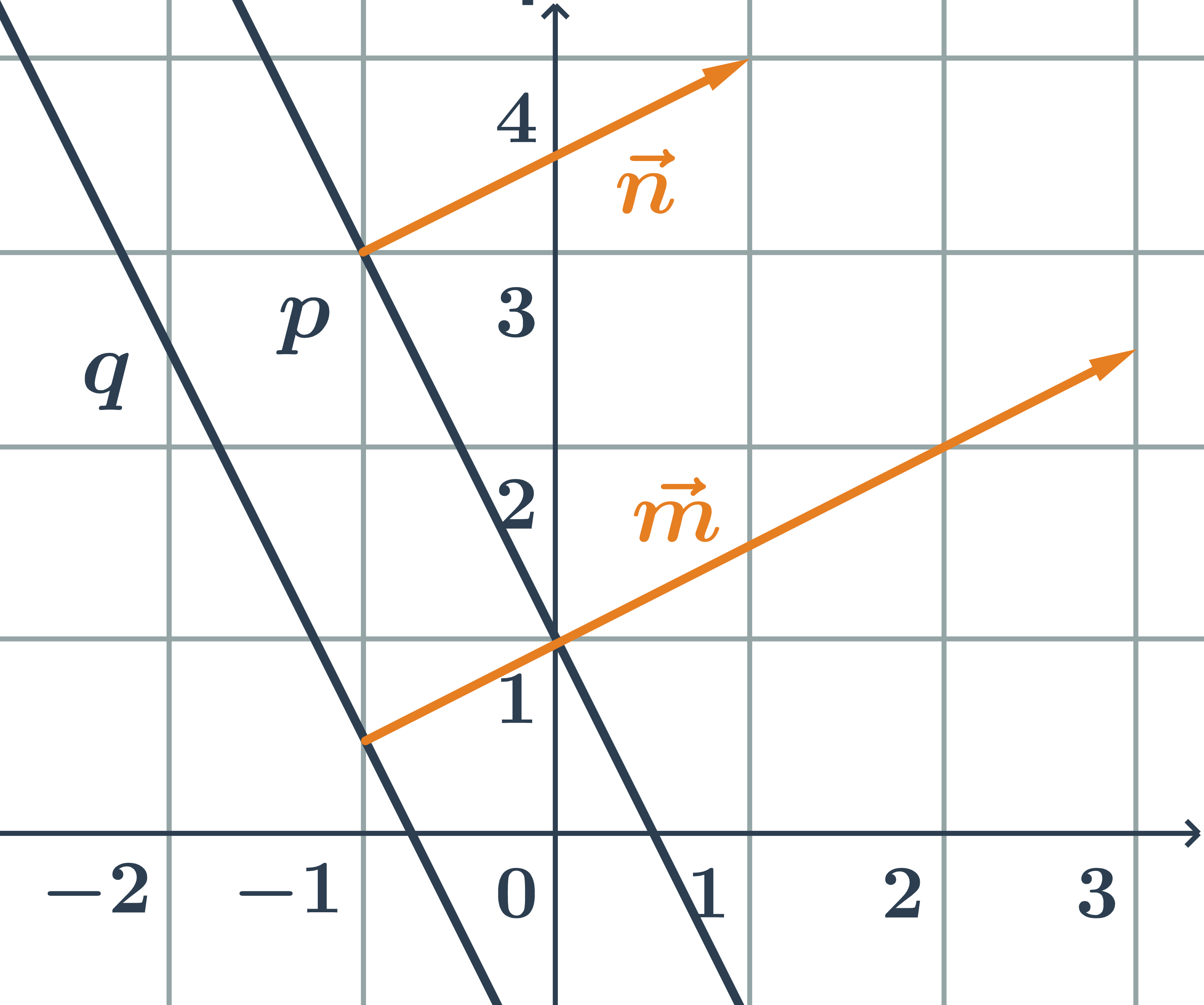
Určite vzájomnú polohu dvoch priamok daných všeobecnými rovnicami p: 2x+y-1=0 a q:4x+2y+3=0.
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor priamky q:\hspace{0.25cm}\vec{m}=(4;2)
- Priamky p a q sú rovnobežné, pretože ich normálové vektory sú kolineárne.
- Overíme, že priamky nie sú totožné. Stačí určiť, či bod, ktorý leží na jednej priamke neleží na priamke druhej.
- Na priamke p leží napríklad bod A=[0;1].
- Overíme, či A leží na p dosadením súradníc bodu A do rovnice priamky p: 4\cdot0+2\cdot1+3\neq 0
- A nespĺňa rovnicu, takže neleží na priamke q \Rightarrow priamky nie sú totožné
Rôznobežky zadané parametrickými rovnicami
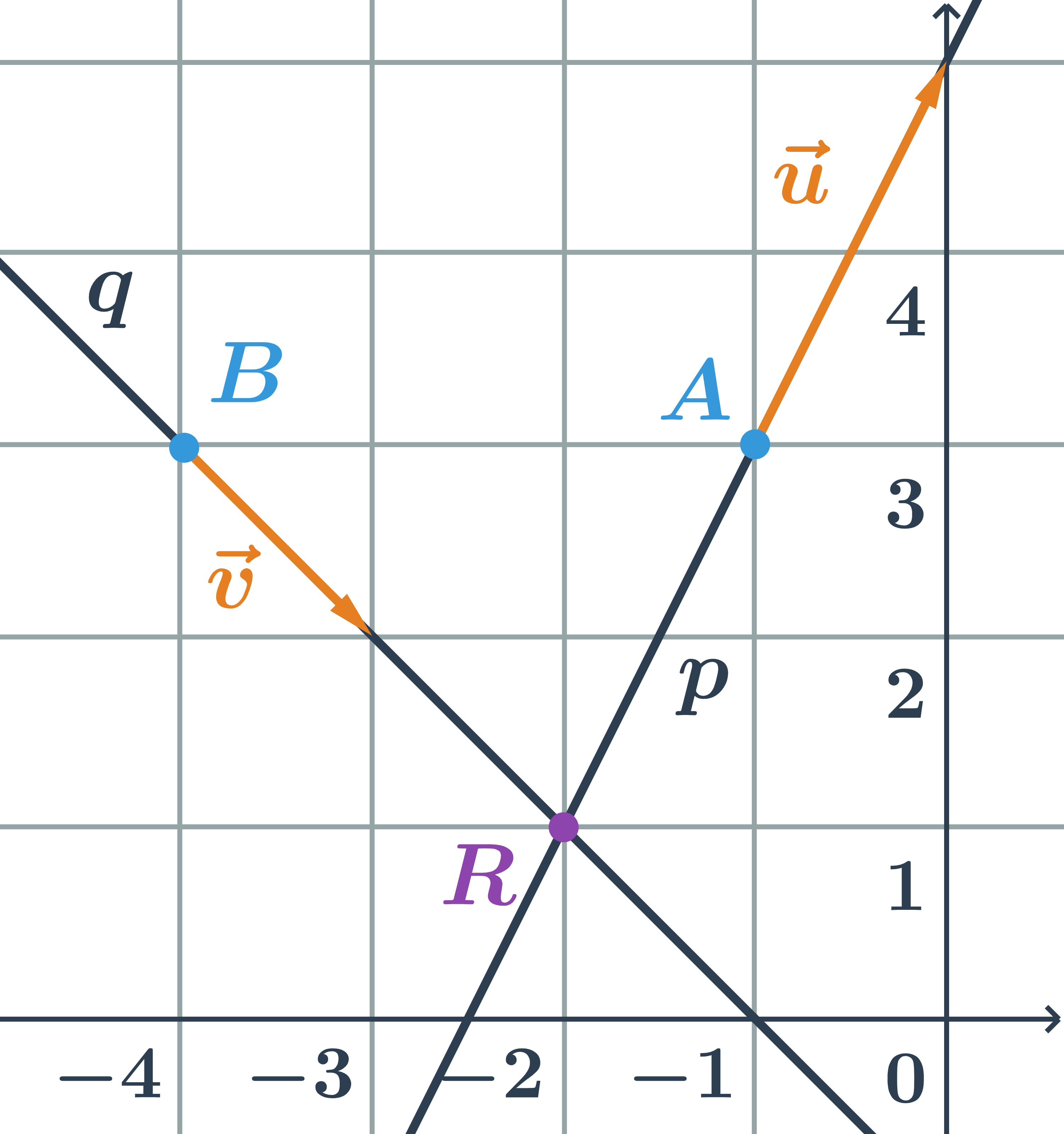
Určite vzájomnú polohu priamok p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-1+t\\y&=&\hspace{0.25cm}3+2t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&-4+s\\y&=&\hspace{0.25cm}3-s\\&&\hspace{0.25cm}s\in\mathbb{R}\end{array}
smerový vektor priamky p:\hspace{0.25cm}\vec{u}=(1;2)
smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(1;-1)
Priamky p a q sú rôznobežné, pretože ich smerové vektory nie sú kolineárne.
Priesečník priamok spĺňa rovnice oboch priamok, teda každú z jeho súradníc je možné vyjadriť dvomi spôsobmi, dostávame nasledujúcu sústavu rovníc: \begin{array}{lrr}-1+t&=&-4+s\\\hspace{0.25cm}3+2t&=&3-s\end{array}
Sústavu môžeme vyriešiť sčítaním oboch rovníc: 2+3t=-1\Rightarrow3+3t=0\Rightarrow t=-1
Výsledný parameter t dosadíme do parametrických rovníc ktorejkoľvek z priamok a dostaneme súradnice x,y priesečníka.
Priesečník priamok p a q je bod R=[-2;1].
Rôznobežky zadané všeobecnými rovnicami
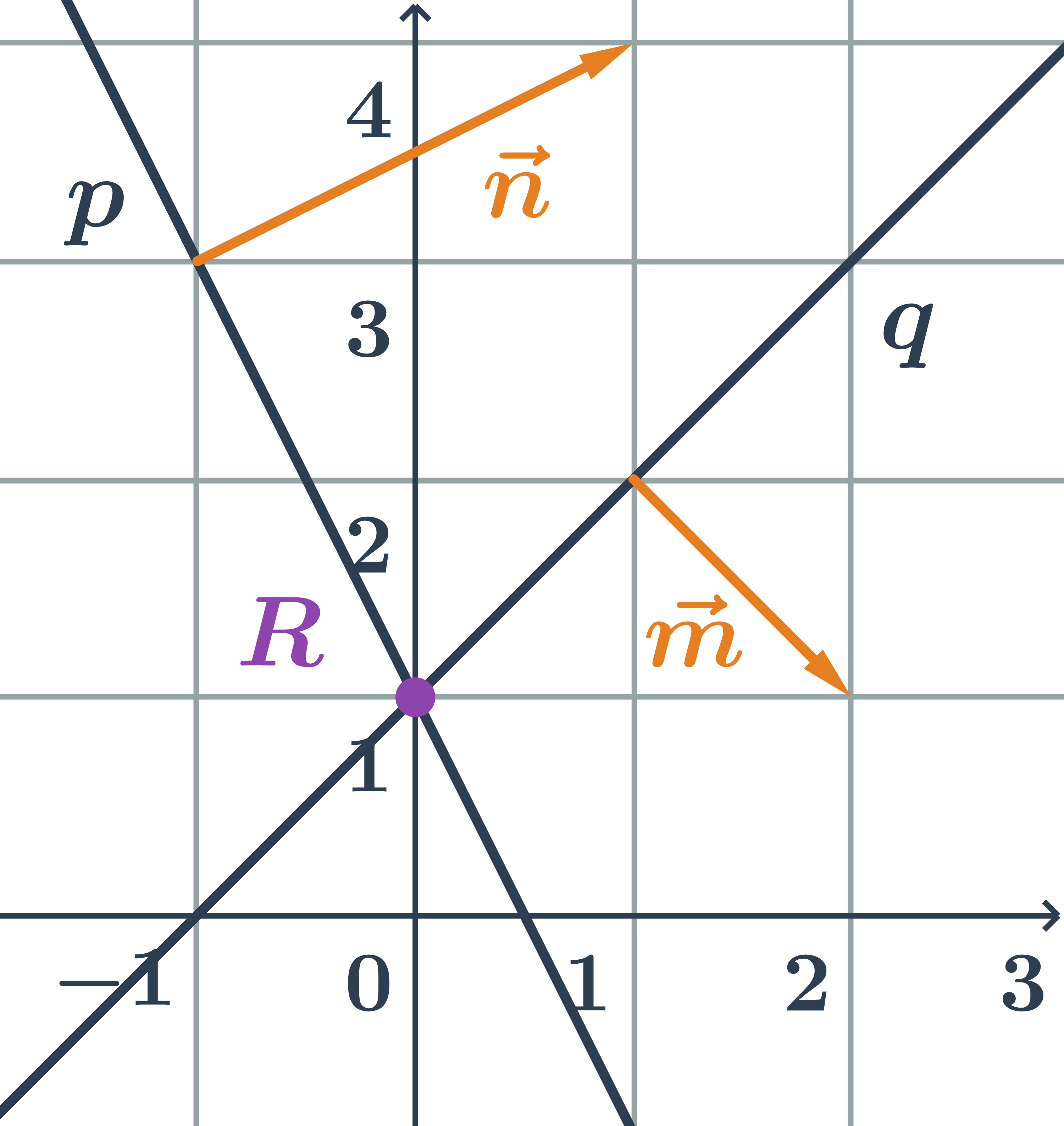
Určíme vzájomnú polohu dvoch priamok zadaných všeobecnými rovnicami p: 2x+y-1=0 a q:x-y+1=0.
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor priamky q:\hspace{0.25cm}\vec{m}=(1;-1)
- Priamky p a q sú rôznobežné, pretože ich normálové vektory nie sú kolineárne.
- Priesečník priamok spĺňa rovnice oboch priamok, teda jeho súradnice sú riešením sústavy: \begin{array}{rrr}2x+y-1&=&0\\x-y+1&=&0\end{array}
- Môžeme vyriešiť sčítaním oboch rovníc: 3x=0\Rightarrow x=0
- Priesečník priamok p a q je bod R=[0;1]
Priamka daná všeobecnou rovnicou a druhá parametricky – prvý príklad
Určite vzájomnú polohu priamok p,q zadaných takto:
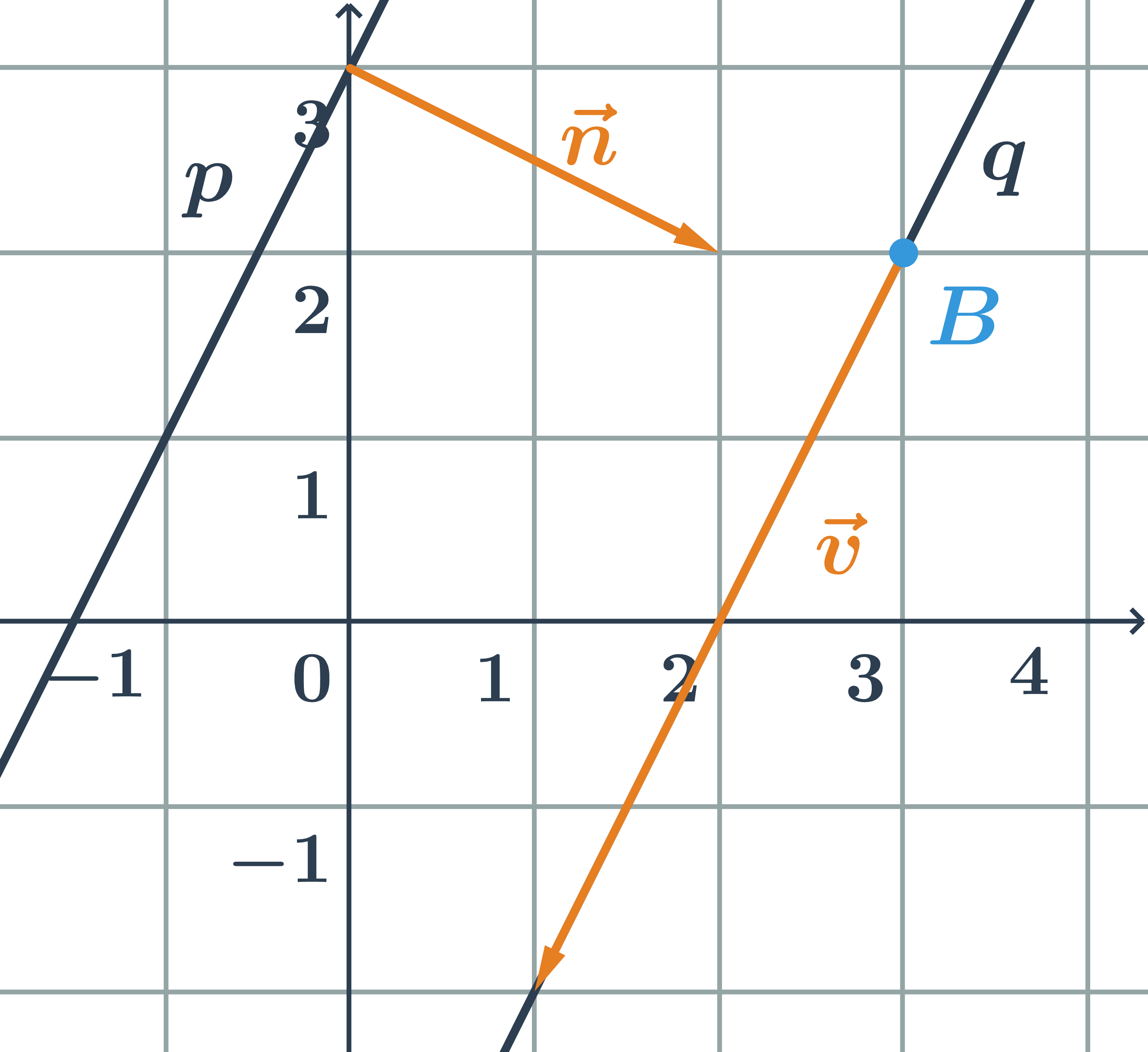
\hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\\&&t\in\mathbb{R}\end{array}
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(2;-1)
- smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(-2;-4)
- Priamky p a q sú rovnobežné, pretože ich smerové vektory sú kolineárne. Preto je normálový vektor jednej priamky kolmý na smerový vektor druhej priamky.
- Overíme, že priamky nie sú totožné: stačí určiť, či bod, ktorý leží na jednej priamke neleží na priamke druhej.
- Na priamke q leží napríklad bod B=[3;2].
- Na priamke p tento bod neleží, čo zistíme dosadením súradníc bodu B do rovnice priamky: 2\cdot3-2+3\neq 0
- Bod B nespĺňa rovnicu, takže neleží na priamke p \Rightarrow priamky nie sú totožné
Priamka daná všeobecnou rovnicou a druhá parametricky – druhý príklad
Určite vzájomnú polohu priamok p,q zadaných:
\hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\\&&\hspace{0.28cm}t\in\mathbb{R}\end{array}
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(1;-3)
- smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(1;2)
- Priamky p a q sú rôznobežné, pretože ich smerové vektory nie sú kolineárne. Vyplýva z toho, že normálový vektor jednej priamky nie je kolmý na smerový vektoru druhej priamky.
- Priesečník priamok spĺňa rovnice oboch priamok, teda jeho súradnice nájdeme tak, že parametrické vyjadrenie priamky q dosadíme do všeobecnej rovnice priamky p: \begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Priesečník priamok p a q je bod R=[3;2]
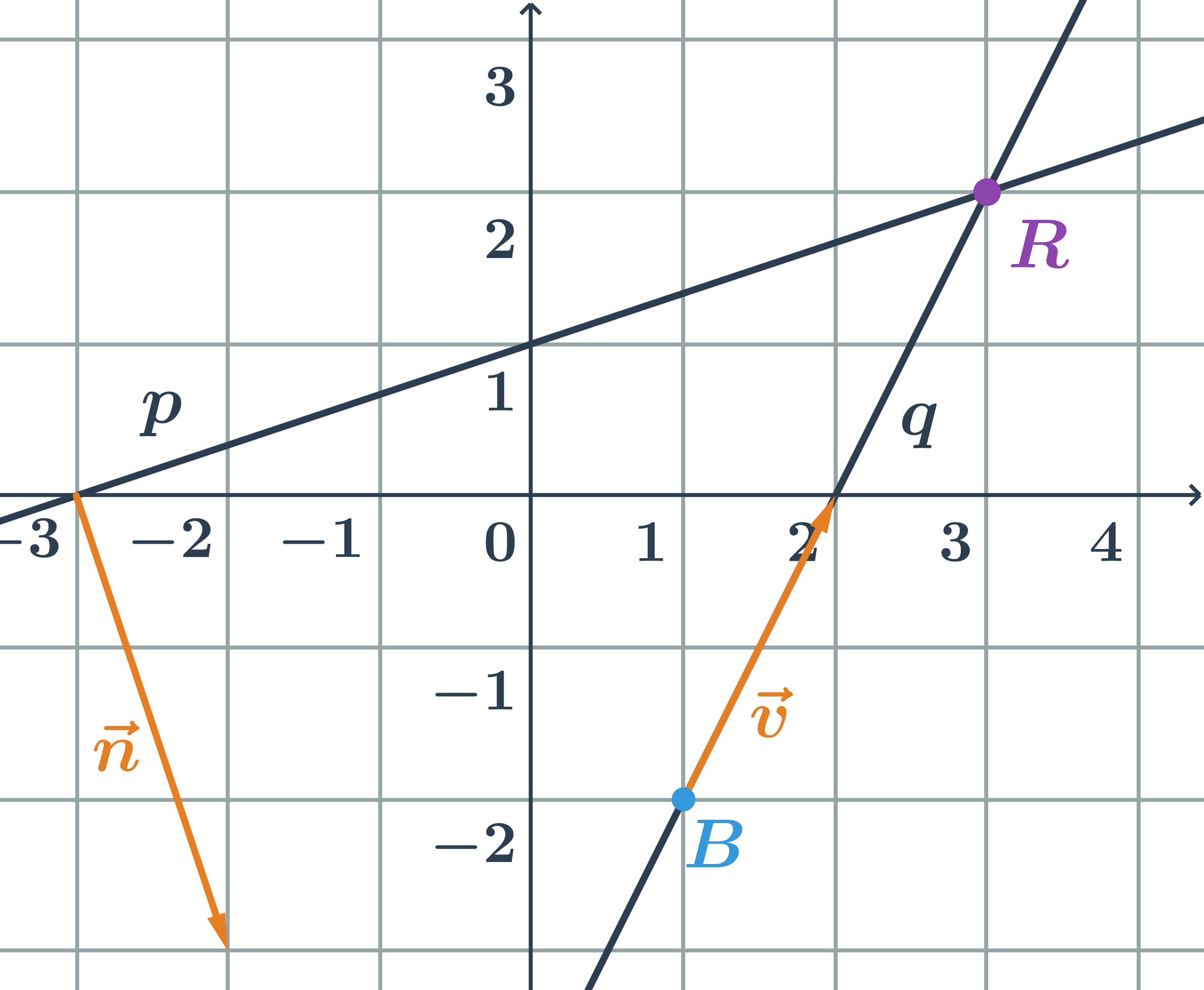
Súvislosť počtu spoločných bodov priamok s počtom riešení sústavy rovníc
Na určenie spoločného bodu (bodov) dvoch priamok, vždy riešime sústavu rovníc. Táto sústava môže mať:
- jedno riešenie – priamky sú rôznobežné
- žiadne riešenie – priamky sú rovnobežné
- nekonečne veľa riešení – priamky sú totožné
Počet spoločných bodov – prvý príklad
Hľadáme priesečník(y) priamok p,q zadaných ako: \hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\end{array}
- Dosadíme parametrické vyjadrenie do všeobecnej rovnice a riešime sústavu rovníc:
\begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Jedno riešenie \Rightarrow rôznobežné priamky
Počet spoločných bodov – druhý príklad
Hľadáme priesečník(y) priamok p,q zadaných ako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\end{array}
- Dosadíme parametrické vyjadrenie do všeobecnej rovnice a riešime sústavu rovníc:
\begin{array}{rrl}2(3-2t)-(2-4t)+3&=&0\\6-4t-2+4t+3&=&0\\7&=&0\end{array}
- Žiadne riešenie \Rightarrow rôzne rovnobežné priamky
Počet spoločných bodov – tretí príklad
Hľadáme priesečník(y) priamok p,q zadaných ako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3+t\\y&=&9+2t\end{array}
- Dosadíme parametrické vyjadrenie do všeobecnej rovnice a riešime sústavu rovníc:
\begin{array}{rrl}2(3+t)-(9+2t)+3&=&0\\6+2t-9-2t+3&=&0\\0&=&0\end{array}
- Nekonečne veľa riešení \Rightarrow totožné priamky
Vzájomná poloha priamok v rovine (ťažké)

