
Grafy lineárnych lomených funkcií

Grafom lineárnej lomenej funkcie je hyperbola, ktorá má asymptoty rovnobežné so súradnicovými osami x a y.
Asymptota rovnobežná s osou y prechádza bodom, ktorý nepatrí do definičného oboru a má teda rovnicu: x =-\frac{d}{c}.
Na nájdenie rovnice asymptoty rovnobežnej s osou x vydelíme čitateľa a menovateľa a funkčný predpis y =\frac{ax+b}{cx+d} upravíme na tvar y =\frac{a}{c}+\frac{n}{ax+b}. Asymptota rovnobežná s osou x má rovnicu: y =\frac{a}{c}.
Priesečník grafu s osou x je bod, pre ktorý ax+b=0. V tomto bode je hodnota funkcie nulová, teda čitateľ zlomku \frac{ax+b}{cx+d} je nulový.
Priesečník grafu s osou y je bod, ktorý dostaneme dosadením hodnoty x=0 do funkčného predpisu.
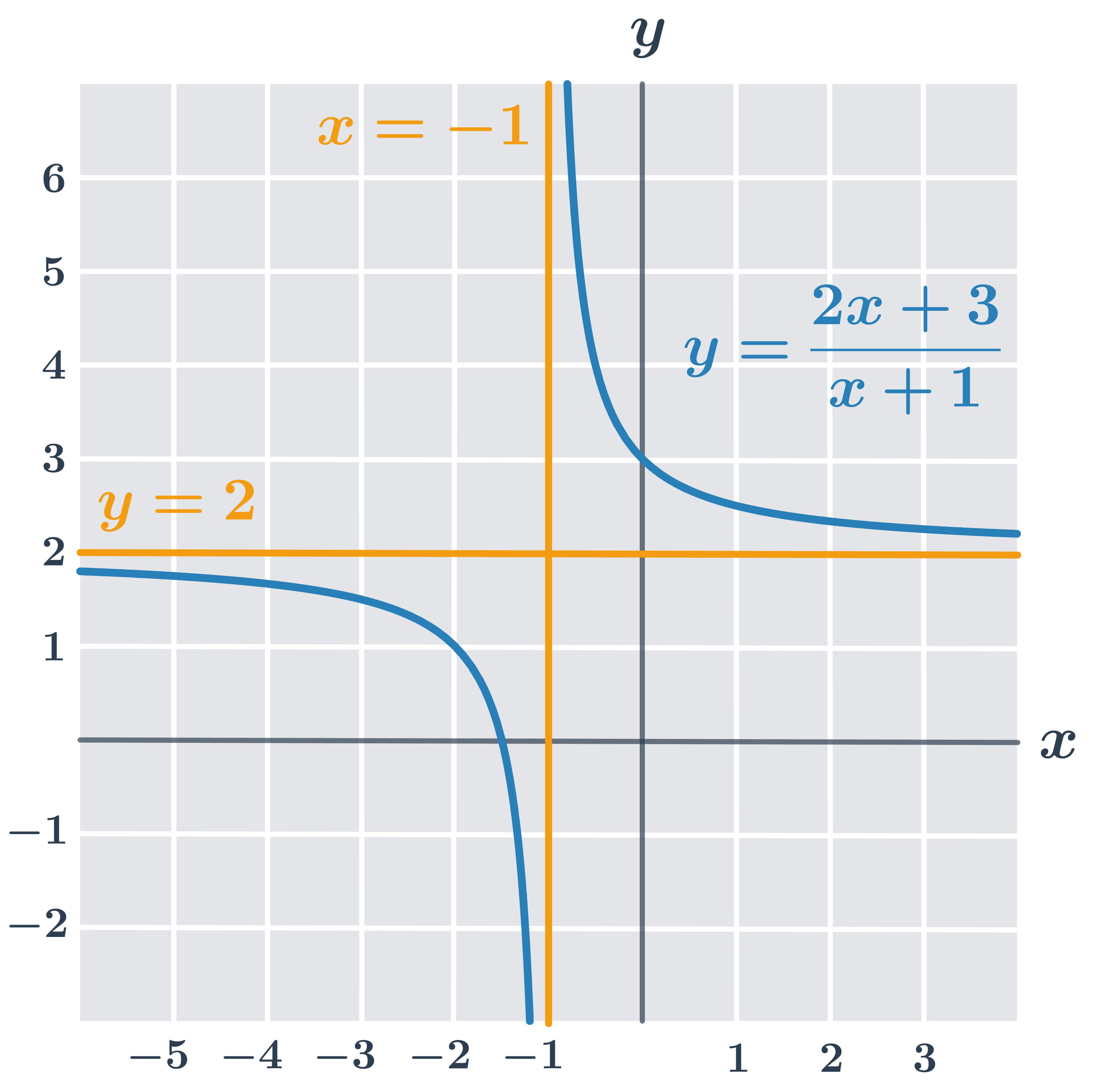
Príklad – funkcia y =\frac{2x+3}{x+1}
Rozoberme si graf funkcie z obrázka vyššie:
- definičný obor D(f)=\R - \{-1\}, pretože x+1\neq0
- asymptota rovnobežná s osou y má rovnicu x =-1 (pre x=-1 nie je funkcia definovaná, toto číslo neleží v jej definičnom obore)
- asymptota rovnobežná s osou x má rovnicu y =2, čo zistíme úpravou funkčného predpisu: y =\frac{2x+3}{x+1}=2+\frac{1}{x+1}
- priesečník grafu s osou x je bod [0;-\frac{3}{2}] (riešenie rovnice: 2x+3=0)
- priesečník grafu s osou y je bod [3;0], dosadením hodnoty x=0 do y =\frac{2x+3}{x+1}
Zatvoriť












