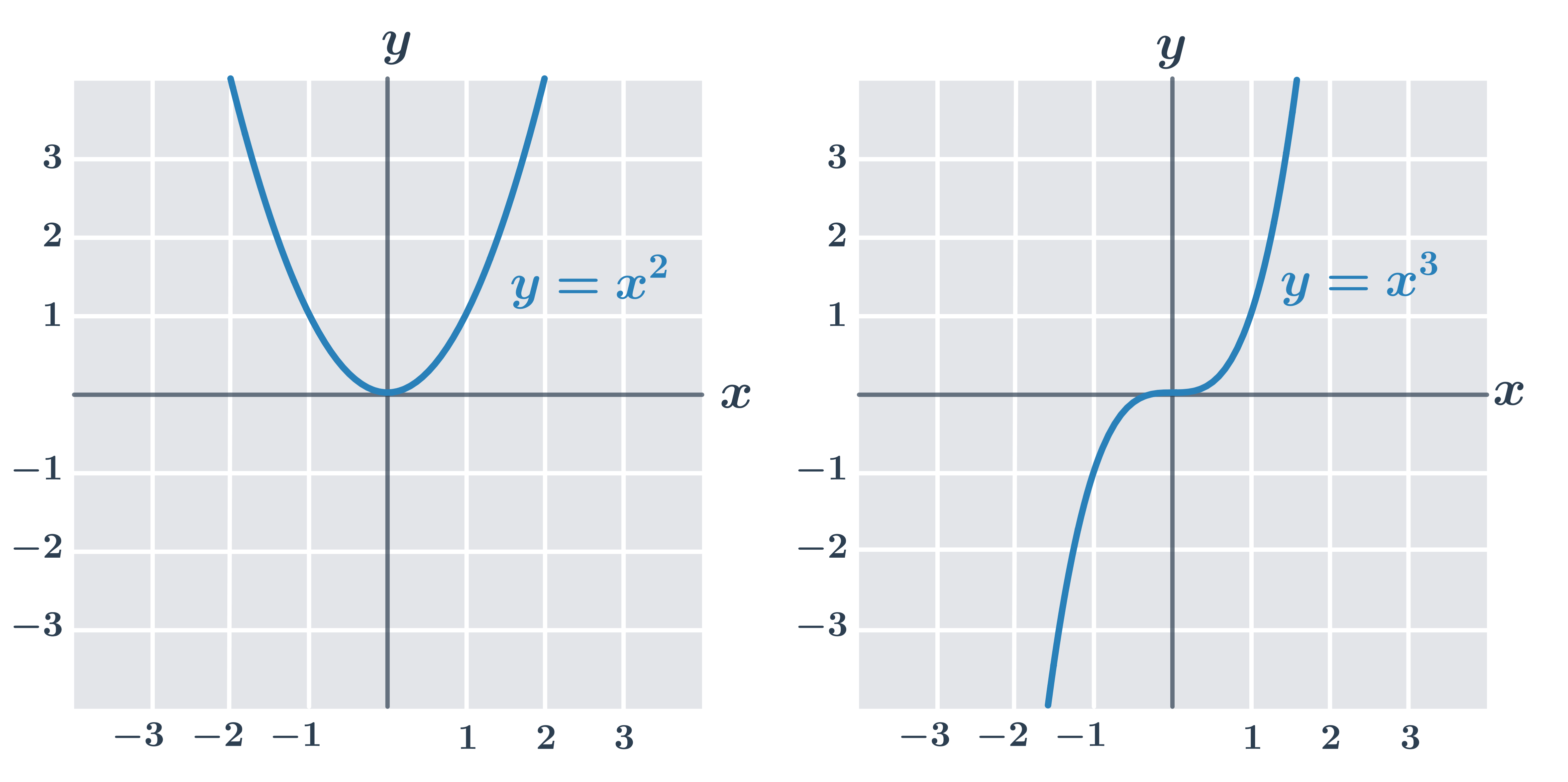Výborne, je dosiahnutý %% štít
Funkcie » Presúvanie »
Funkcie
Presúvanie
Precvičujte neobmedzeneVáš denný počet odpovedí je obmedzený. Pre navýšenie limitu alebo prístup do svojho účtu s licenciou sa prihláste.
Prihlásiť sa
G41QR kód
Kód / krátka adresa
Skopírujte kliknutím.
Grafy mocninových funkcií
Grafy základných mocninových funkcií y= x^n
pre párne n – graf je súmerný podľa osi y, D(f)=\R, H(f)=\langle0, \infty)
pre nepárne n – graf je súmerný podľa počiatku, D(f)=\R, H(f)=\R
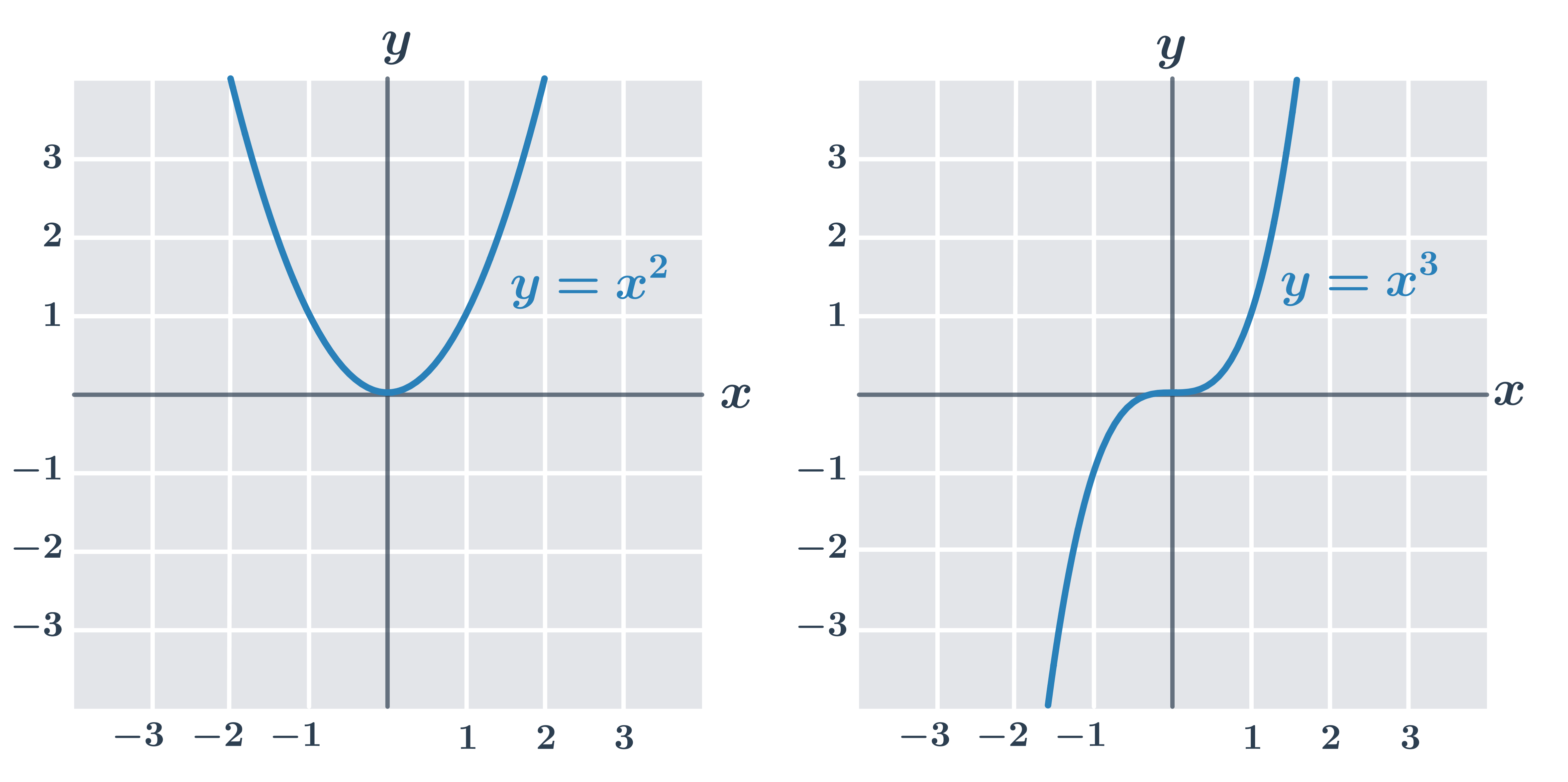
Grafy mocninových funkcií so záporným exponentom y= x^{-n}
pre párne n – graf súmerný podľa osi y, D(f)=\R- \{0\}, H(f)=\langle0, \infty)
pre nepárne n – graf súmerný podľa počiatku, D(f)=\R - \{0\}, H(f)=\R - \{0\}
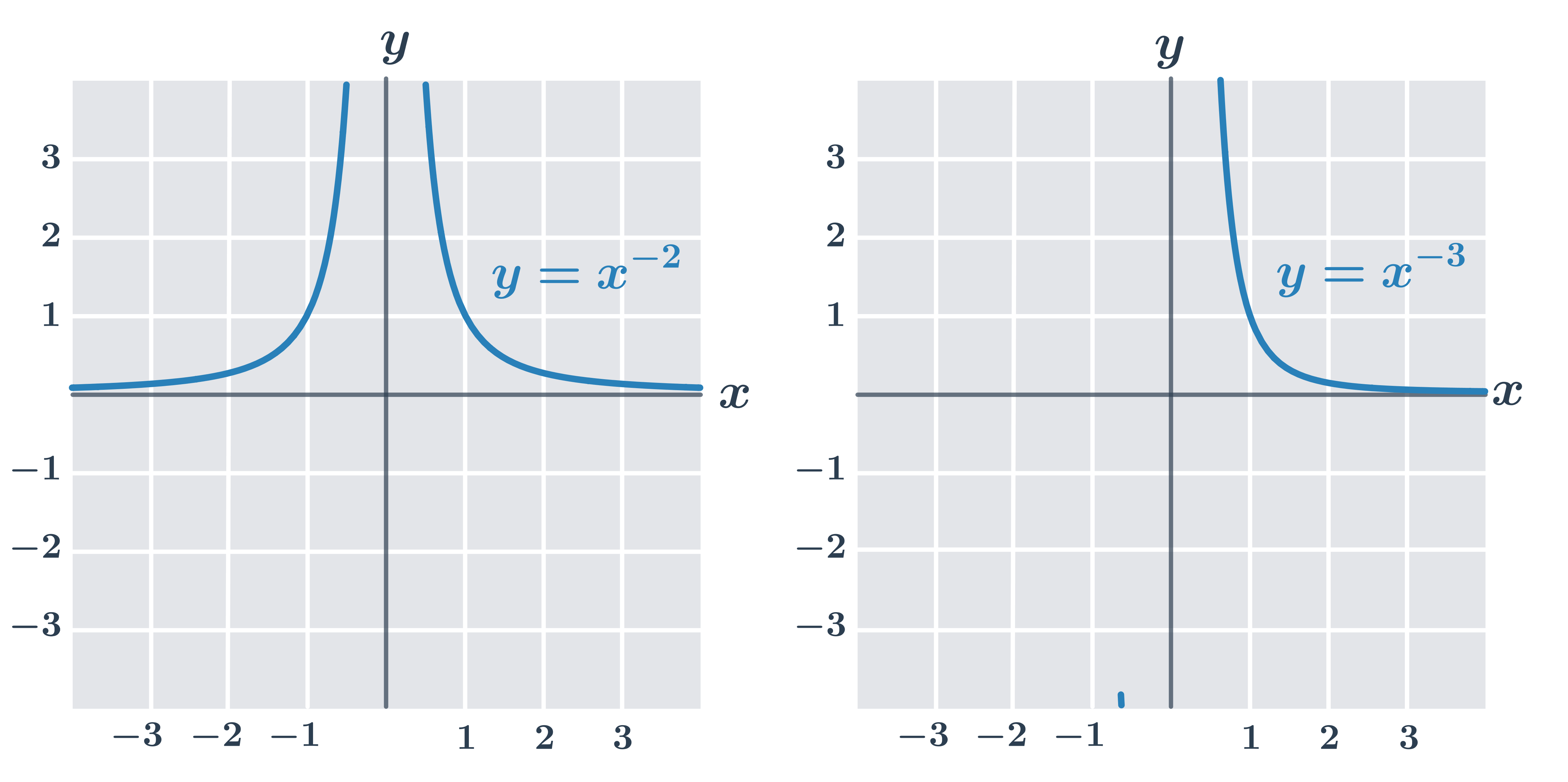
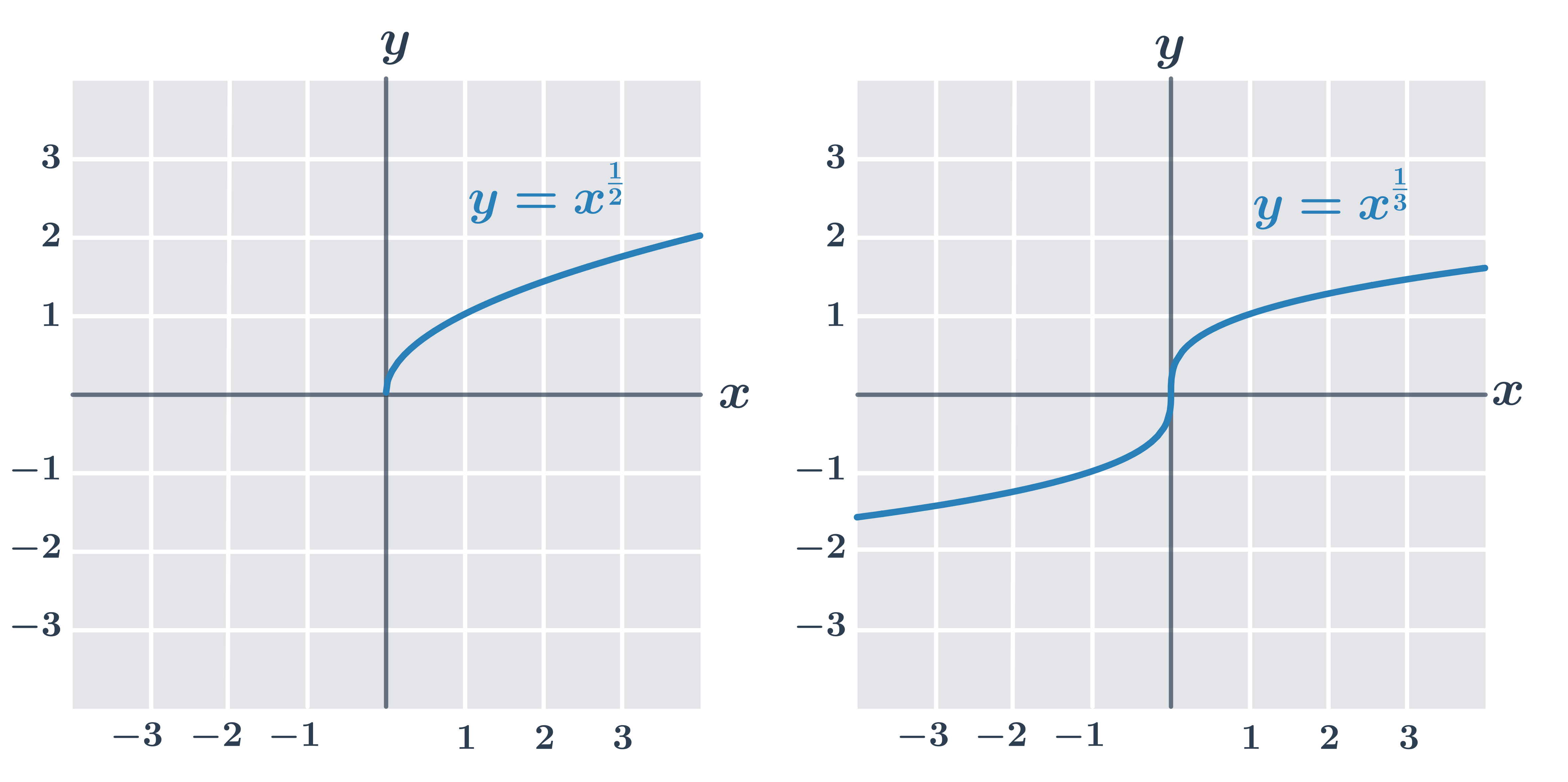
Grafy funkcií y= x^{\frac{1}{n}}:
pre párne n – funkcia y= x^{\frac{1}{n}} definovaná na kladných číslach, D(f)=\langle0, \infty), H(f)=\langle0, \infty)
pre nepárne n – funkcia y=x^n je jednoduchá, preto by sme mohli definovať n-tú odmocninu aj pre záporné čísla, ale často sa všetky n-té odmocniny pre párne aj nepárne n definujú pre jednoduchosť iba na intervale [0,\infty) (napr. ako príprava na prácu s mocninovými funkciami so všeobecnejšími racionálnymi exponentami) .
Poznámka: výpočty s mocninami a odmocninami
Pri výpočtoch s mocninami a odmocninami musíme byť obozretní; veľa pravidiel platí pre nezáporný základ (ak počítame s odmocninami), prípadne kladný základ (nulu môžeme odmocňovať, ale nesmieme deliť nulou). Príklady:
súčin odmocnín je odmocnina súčinu: pre nezáporné čísla ako základy odmocnín pravidlo platí, ak by sme chceli použiť pre záporný základ, nemusia nám v obore reálnych čísel vychádzať zmysluplné veci: \sqrt{-2} nie je definovaná, ale \sqrt{(-2)\cdot(-2)} je \sqrt{4} = 2
racionálne exponenty: malo by x^{\frac{2}{6}} byť to isté ako x^{\frac{1}{3}}? Exponent je „rovnaké racionálne číslo“, ale pre záporné x by vychádzali v prípade týchto dvoch predpisov iné funkčné hodnoty (6. odmocnina zo záporného x nie je definovaná, 6. odmocnina z druhej mocniny záporného čísla je kladná, a 3. odmocnina z x by bola pre záporné x záporná).
racionálne exponenty konkrétnejšie: čomu by sa malo rovnať (-8)^{\frac{2}{6}}? Máme (-8)^{\frac{1}{3}}=-2, ale zároveň \sqrt[6]{(-8)^2} = \sqrt[6]{64} = 2. Môžeme mať problém, keď budeme pravidlá, ktoré platia pre mocniny a odmocniny kladných a nezáporných čísel, skúšať používať aj pre záporné základy.
Vplyv úprav funkčného predpisu na graf mocninovej funkcie
Obrázok ukazuje niekoľko úprav funkcie y= x^3:
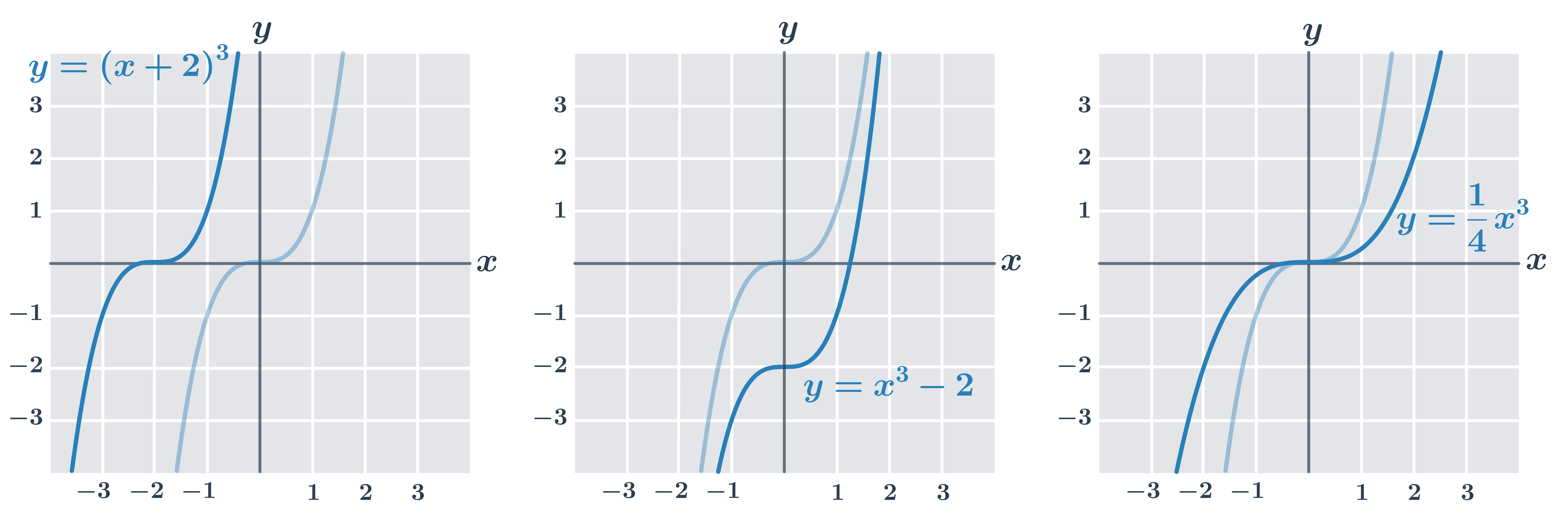
| y= (x+2)^3 | graf je posunutý v smere osi x |
| y=x^3-2 | graf je posunutý v smere osi y |
| y=\frac{1}{4} x^3 | graf bude natiahnutý alebo stlačený v smere osi y (v uvedenom grafe sa funkčné hodnoty zmenšia na štvrtinu, napríklad pre x=2 je hodnota funkcie y=\frac{1}{4} \cdot 2^3=2) |
Grafy mocninových funkcií (ťažké)
Teraz sa už môžu opakovať už vyriešené zadania.