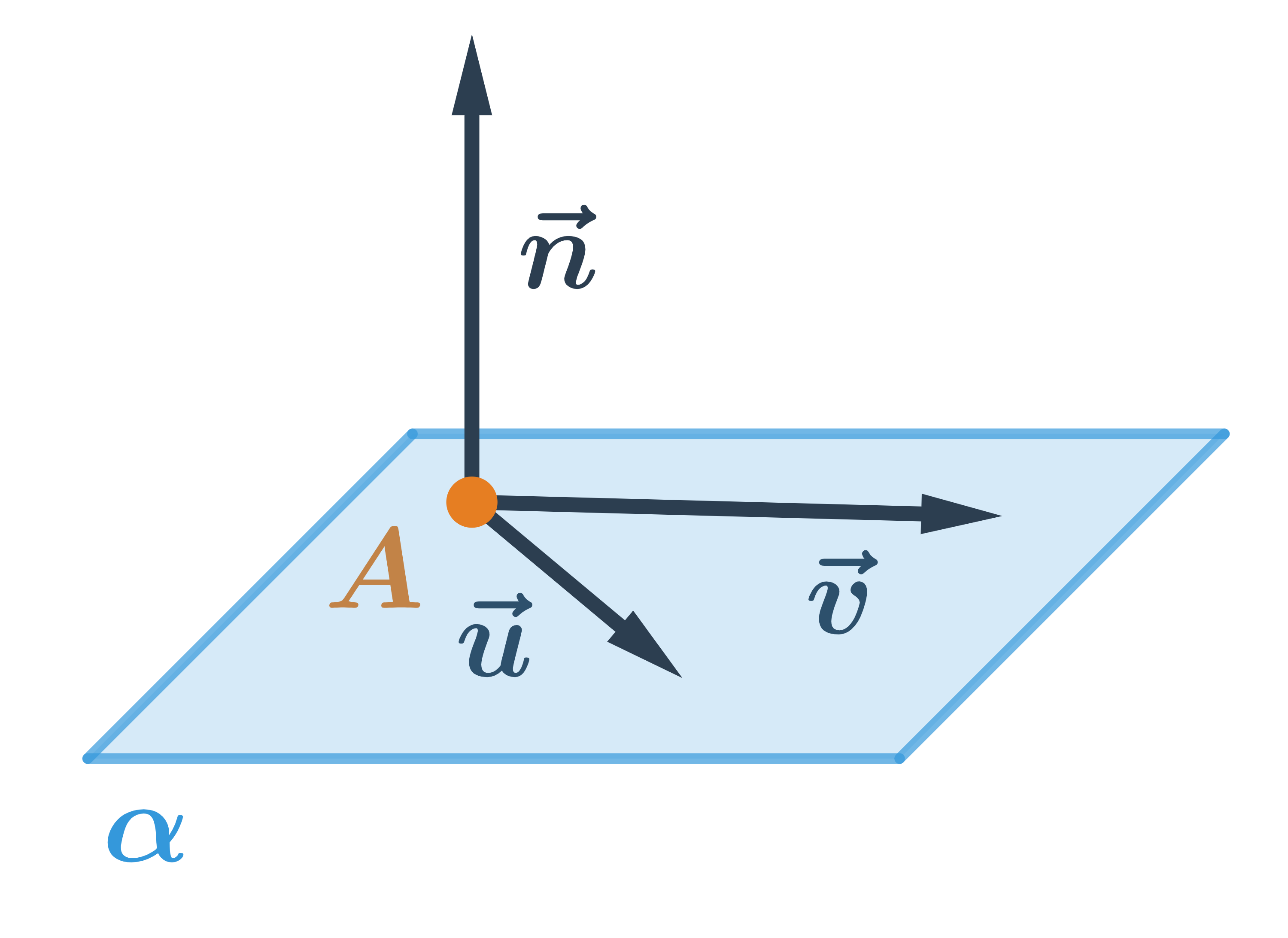
Priamka je jednoznačne určená bodom a dvomi vektormi, ktoré nie sú kolineárne. Na obrázku je rovina \alpha určená bodom A a vektormi \vec{u}, \vec{v}. Každý vektor, ktorý je kolmý na rovinu \alpha sa nazýva normálový vektor roviny \alpha. Na obrázku je normálový vektor \vec{n}.
Parametrické rovnice roviny
Rovina určená bodom A=[a_1;a_2;a_3] a vektormi \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Skrátene môžeme vyjadriť \alpha:X=A+t\vec{u}+s\vec{v}, kde t, s nazývame parametrami.
Všeobecná rovnica roviny
Všeobecná rovnica roviny je v tvare ax+by+cz+d=0, kde konštanty a, b, c sú súradnice normálového vektora a d reálne číslo.
Všeobecná rovnica roviny rovnobežnej s osami x a y
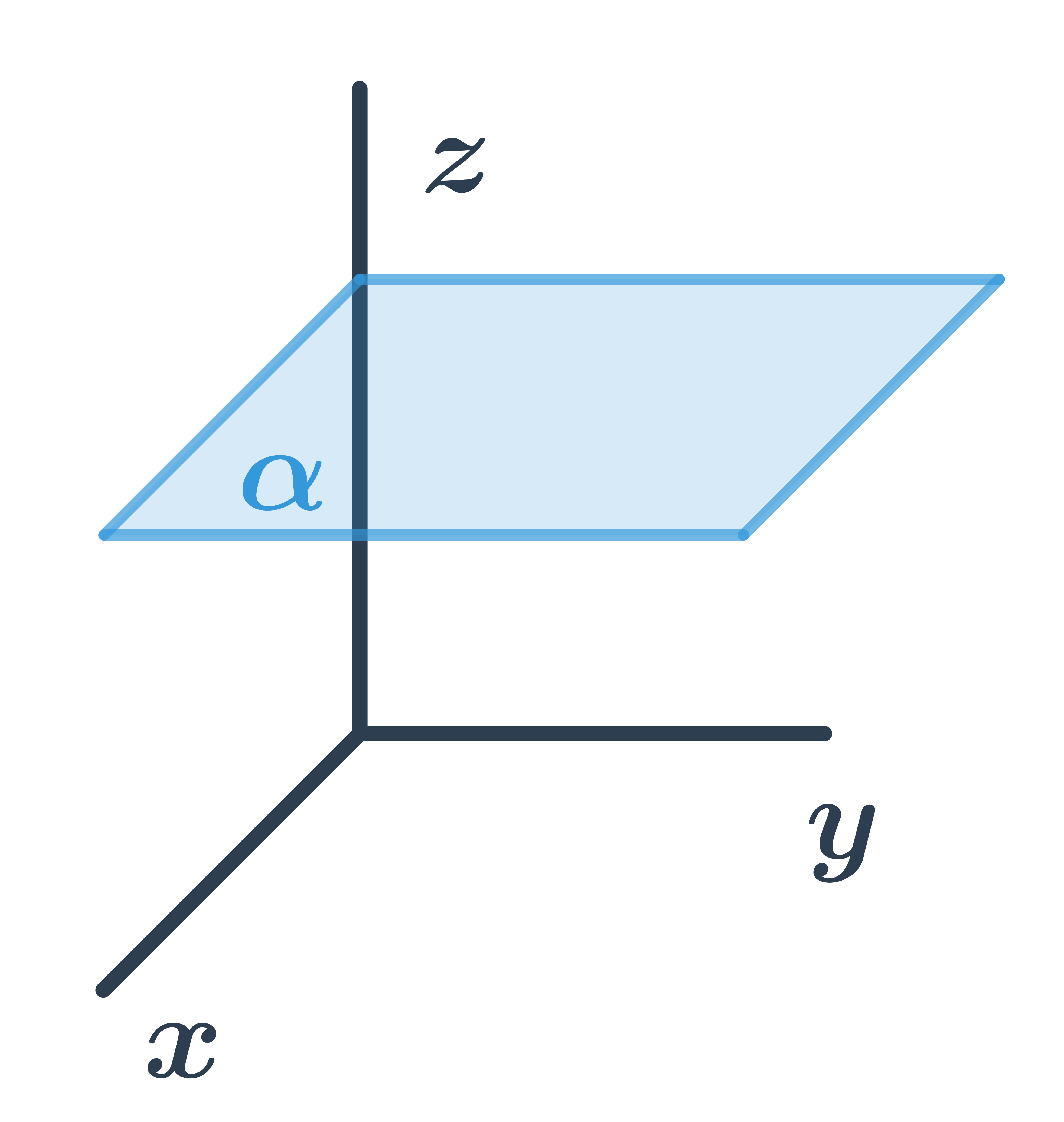
Pre všetky body ležiace v rovine je tretia súradnica rovnaká, teda rovina má všeobecnú rovnicu: z+d=0.
Všeobecná rovnica roviny rovnobežnej s osami x a z
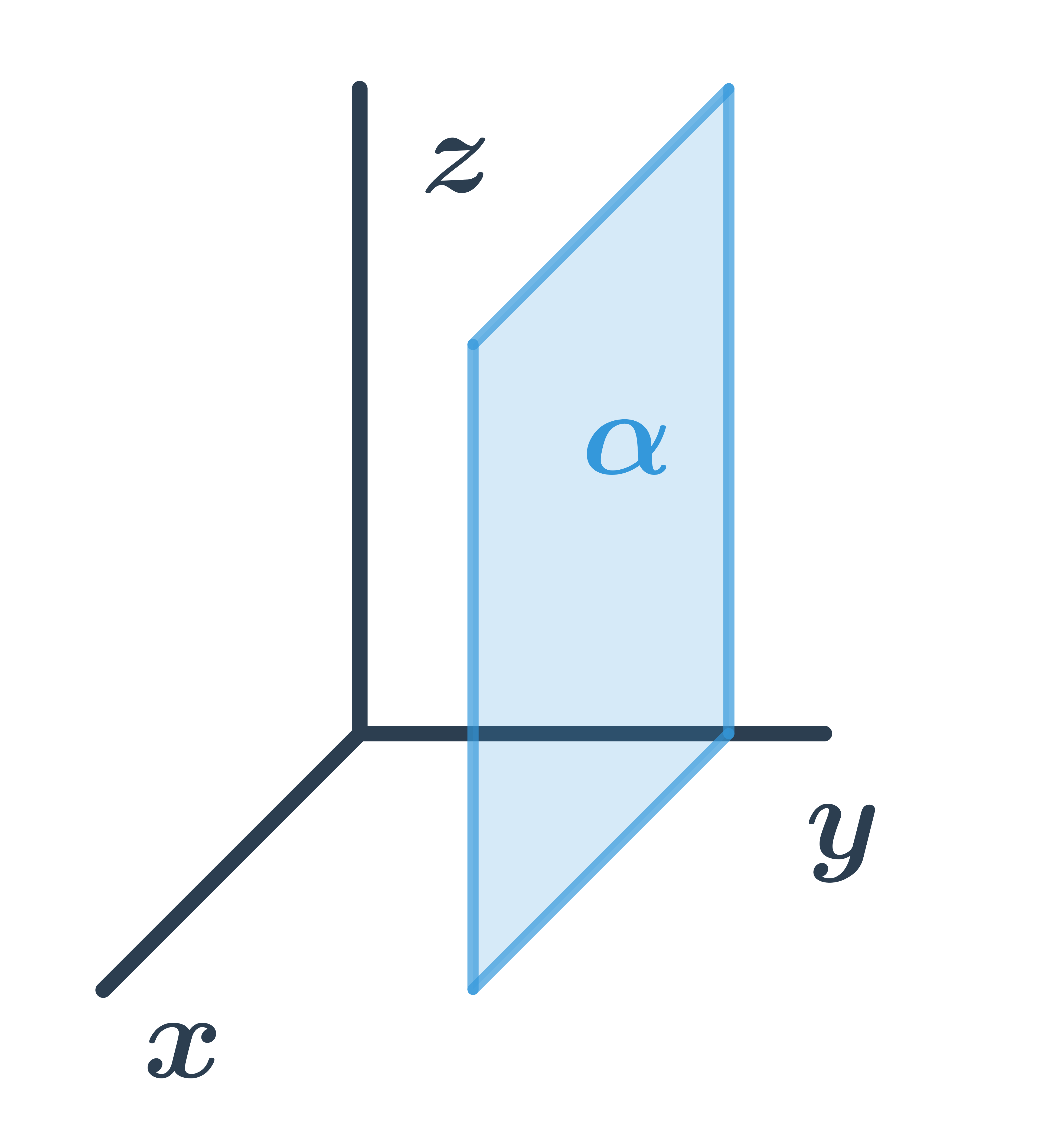
Pre všetky body ležiace v rovine je druhá súradnica rovnaká, teda rovina má všeobecnú rovnicu: y+d=0.
Všeobecná rovnica roviny rovnobežnej s osami y a z
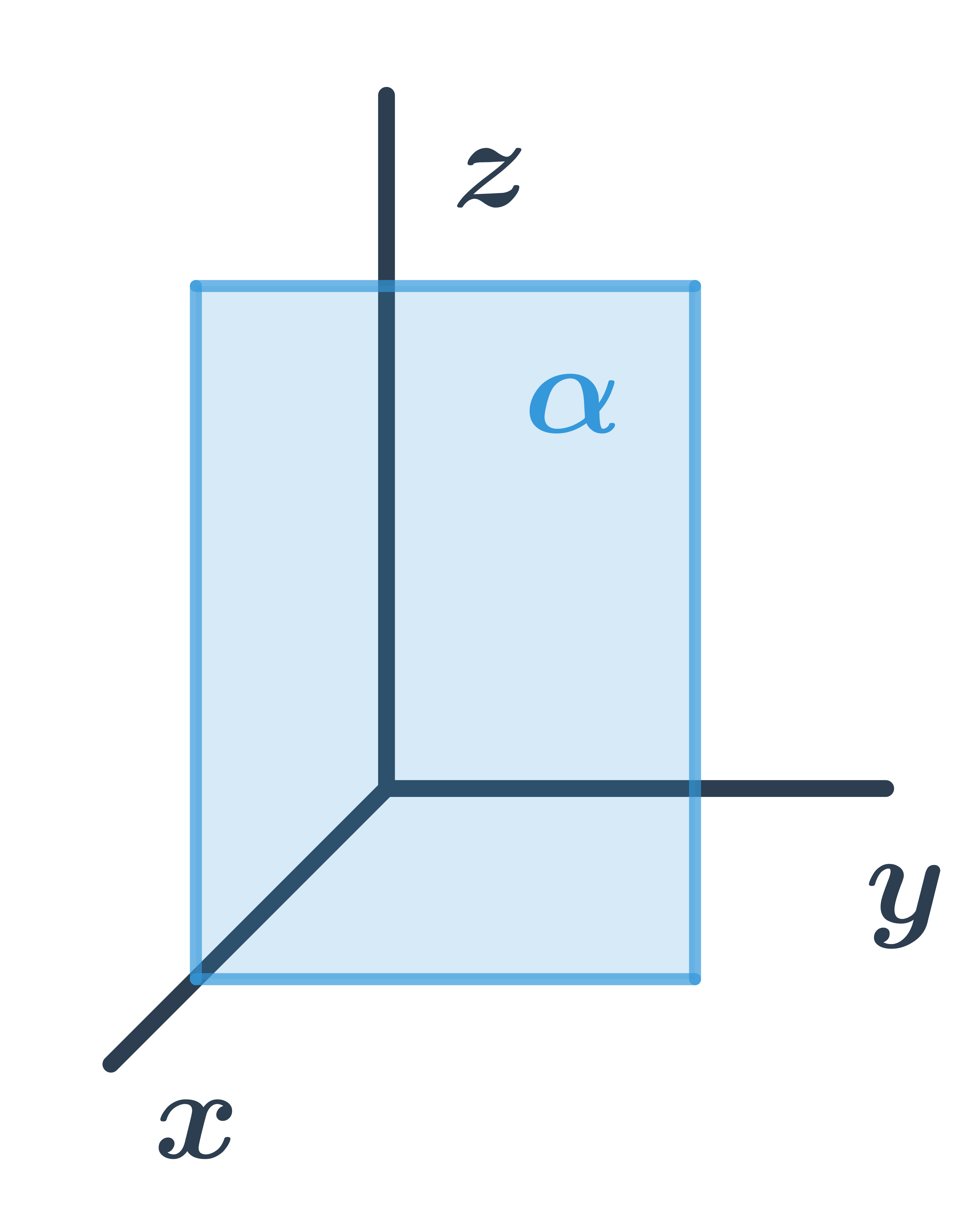
Pre všetky body ležiace v rovine je prvá súradnica rovnaká, teda rovina má všeobecnú rovnicu: z+d=0.
Bod a rovina
Bod M=[m_1;m_2;m_3] leží v rovine, ak jeho súradnice vyhovujú rovnici roviny.
- Ak je rovina daná všeobecnou rovnicou ax+by+cz+d=0, pre súradnice bodu, ktorý leží na priamke platí: a\cdot m_1+b\cdot m_2+c\cdot m_3+d=0
- Ak je rovina daná parametricky, po dosadení súradníc bodu do parametrických rovníc dostaneme sústavu troch rovníc pre dve neznáme t, s, ktorá má presne jedno riešenie (dvojicu reálnych čísel).
Všeobecná rovnica roviny, ktorá prechádza počiatkom
- Rovina prechádza bodom O=[0;0;0], musí teda platiť: a\cdot0+b\cdot0+c\cdot0+d=0\Rightarrow d=0.
- Rovina, ktorá prechádza počiatkom má všeobecnú rovnicu: ax+by+cz=0.
Dve rovnobežné roviny
Normálové vektory dvoch rovnobežných rovín \alpha: a_1x+b_1y+c_1z+d_1=0 a \beta: a_2x+b_2y+c_2z+d_2=0 sú kolineárne, teda súradnice jedného vektora sú k-násobok súradníc druhého vektora. Pre konštanty vo všeobecných rovniciach musí platiť:
\begin{array}{rll}a_2&=&k\cdot a_1\\ b_2&=&k\cdot b_1\\c_2&=&k\cdot c_1\\&&k\in\mathbb{R}\end{array}
Ak by platilo i d_2=k\cdot d_1 roviny sú totožné.













