
Odmocniny

Odmocňovanie v matematike je čiastočne inverznou (opačnou) operáciou k umocňovaniu. Druhá odmocnina z čísla x je také nezáporné číslo a, pre ktoré platí a^2 = x. Druhú odmocninu značíme \sqrt{x}. Príklady:
- \sqrt{9} = 3, pretože 3^2 = 9
- \sqrt{25} = 5, pretože 5^2 = 25
- \sqrt{100} = 10, pretože 10^2 = 100
Všeobecne potom n-tá odmocnina z x je také číslo a, pre ktoré platí a^n = x, n-tú odmocninu značíme \sqrt[n]{x}. Príklady:
- \sqrt[3]{125} = 5, pretože 5^3 = 25
- \sqrt[5]{32} = 2, pretože 2^5 = 32
- \sqrt[4]{10 000} = 10, pretože 10^4 = 10 000
Odmocňovanie má aj geometrický význam. Ak máme štvorec s obsahom S, potom má tento štvorec dĺžku strany rovnú druhej odmocnine \sqrt{S}. Ak máme kocku s objemom V, potom má táto kocka dĺžku hrany rovnú tretej odmocnine \sqrt[3]{V}. Odmocniny často využijeme napríklad pri aplikácii Pytagorovej vety.
Graf funkcie odmocnina
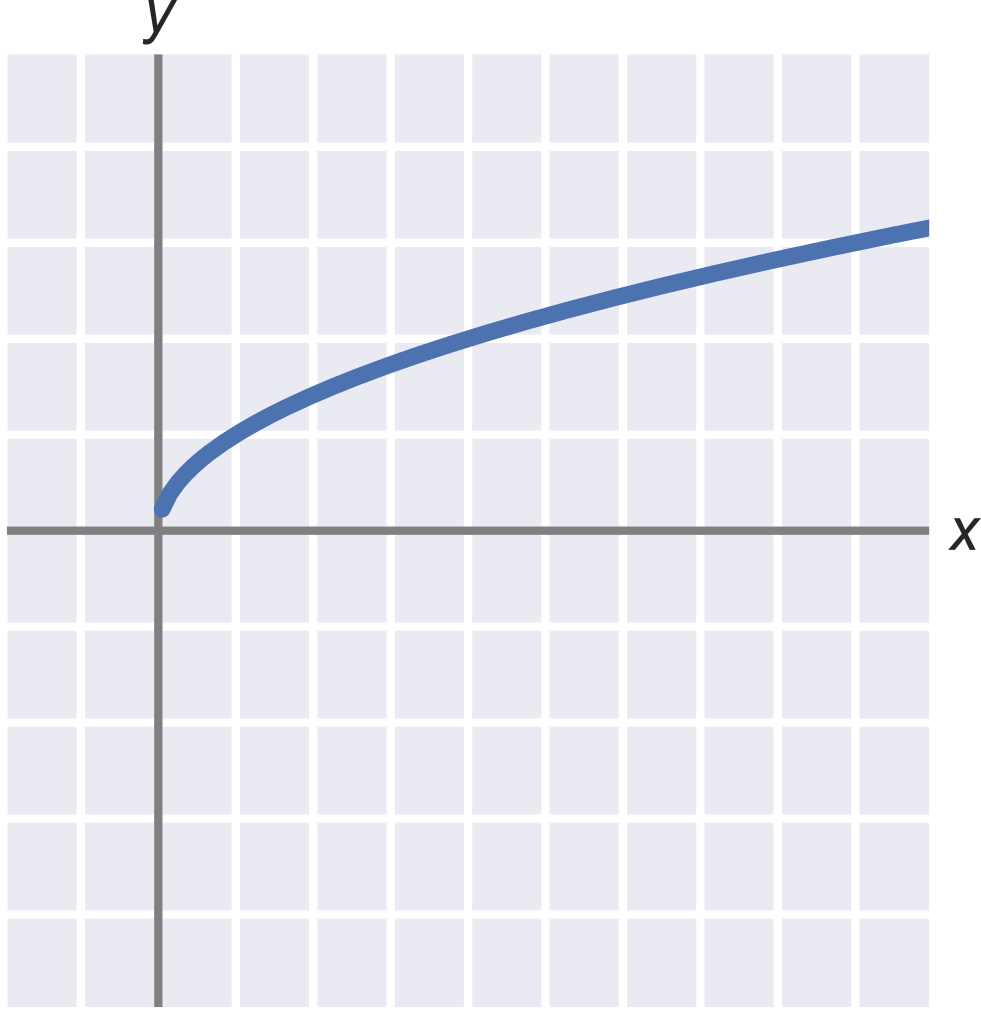
Odmocnina a záporné čísla
Keď hľadáme odmocninu napríklad z 25, tak hľadáme číslo, ktoré po umocnení dá 25. To spĺňa 5\cdot 5, ale tiež (-5)\cdot (-5). Odmocnina je však definovaná ako nezáporné číslo, takže \sqrt{25} = 5.
Druhú odmocninu môžeme počítať len z kladných čísel, pretože akékoľvek číslo umocnené na druhú je kladné. Odmocnina zo záporných čísel nie je definovaná. Alebo vlastne je, ale to musíme zaviesť komplexné čísla (čo je veľmi zaujímavý a užitočný nástroj, ale už trochu pokročilý, takže ho tu nebudeme rozoberať).
Pre bežné reálne čísla môžeme počítať odmocniny zo záporných čísel pre nepárne stupne n. Napríklad:
- \sqrt[3]{-8} = -2, pretože (-2)^3 = -8
- \sqrt[5]{-100 000} = -10, pretože (-10)^5 = -100 000
Zatvoriť










