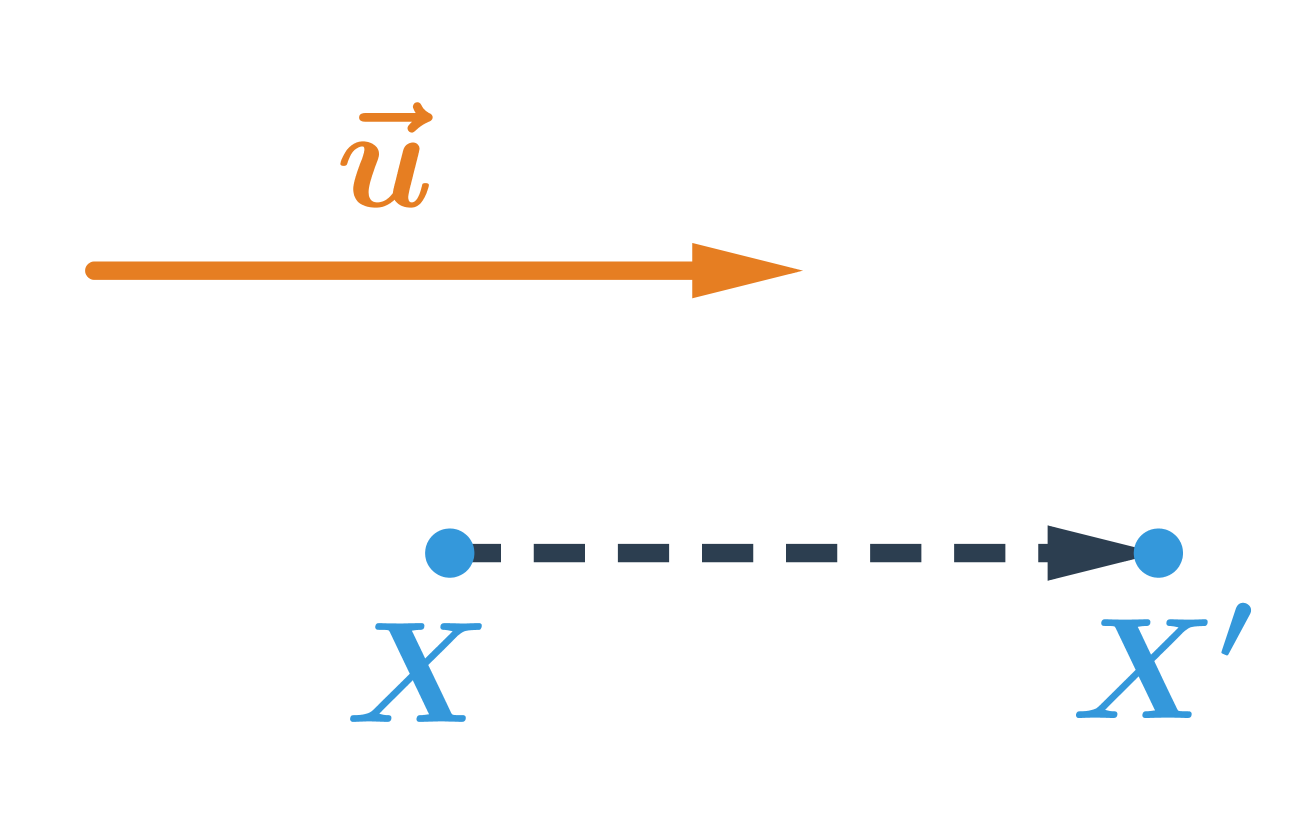Posunutie

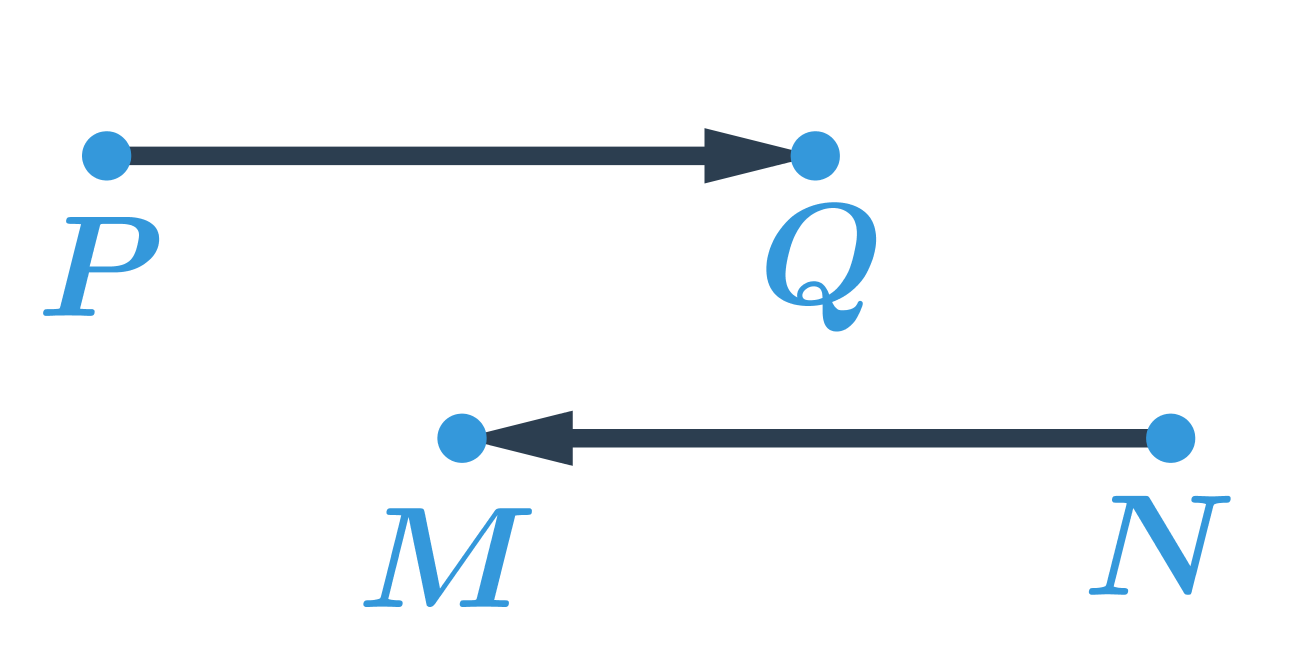
Posunutie je dané orientovanou úsečkou. Táto úsečka určuje smer a dĺžku posunutia. Orientovaná úsečka je úsečka, pri ktorej rozlišujeme, ktorý bod je počiatočný a ktorý koncový. Orientovanú úsečku označíme šípkou, ktorá určí jej smer. Zápis \overrightarrow{PQ} znamená, že počiatočným bodom orientovanej úsečky je bod P a koncovým bodom bod Q. Na obrázku sú orientované úsečky \overrightarrow{PQ} a \overrightarrow{NM}. Tieto úsečky majú rovnakú dĺžku, ale opačný smer.
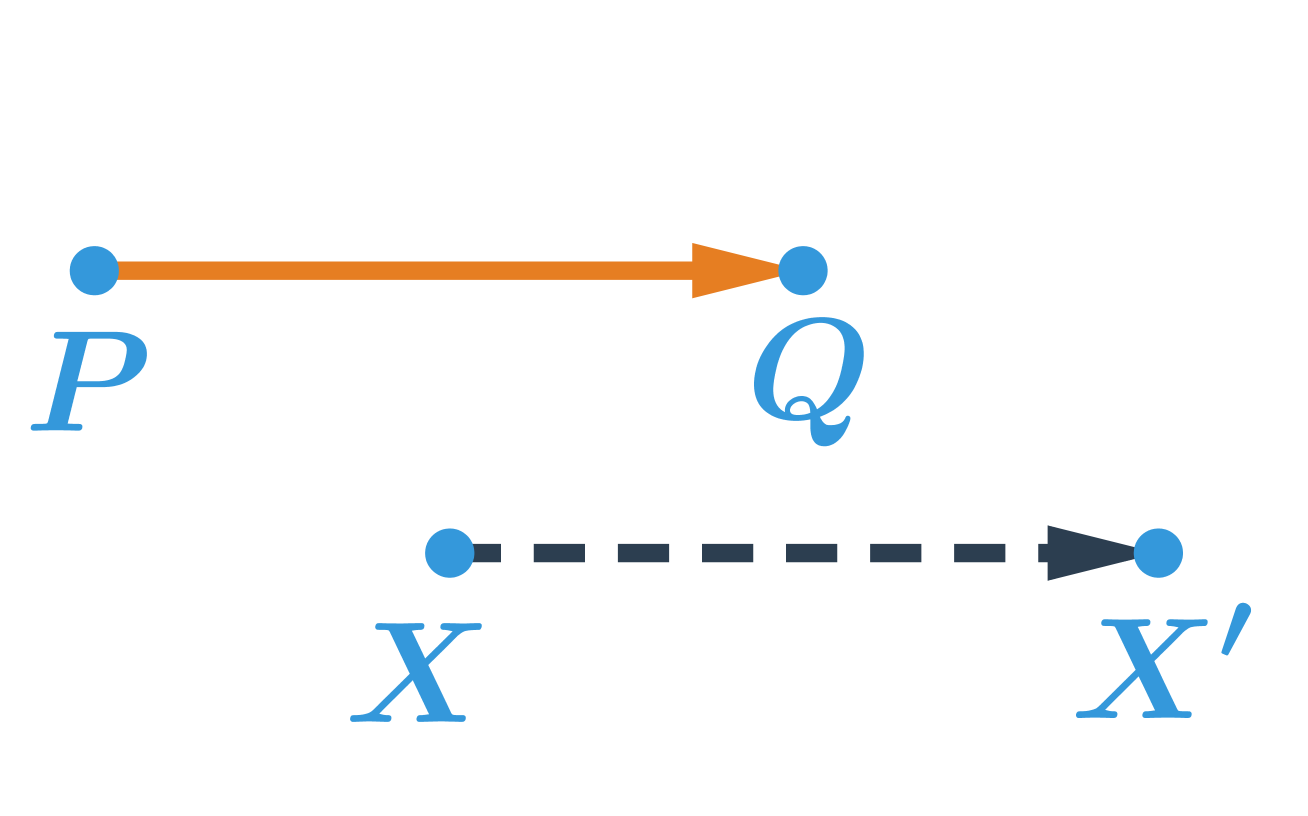
Obrazom bodu X v posunutí, ktoré je určené orientovanou úsečkou \overrightarrow{PQ}, je bod X', pre ktorý platí, že orientovaná úsečka \overrightarrow{XX'} má rovnakú veľkosť a rovnaký smer ako orientovaná úsečka \overrightarrow{PQ}.
Príklad: posunutie bodu
Obrazom bodu X v posunutí, ktoré je určené orientovanou úsečkou \overrightarrow{PQ}, je bod X':
Príklad: posunutie trojuholníka
Obrazom trojuholníka ABC v posunutí, ktoré je určené orientovanou úsečkou \overrightarrow{PQ}, je trojuholník A'B'C': 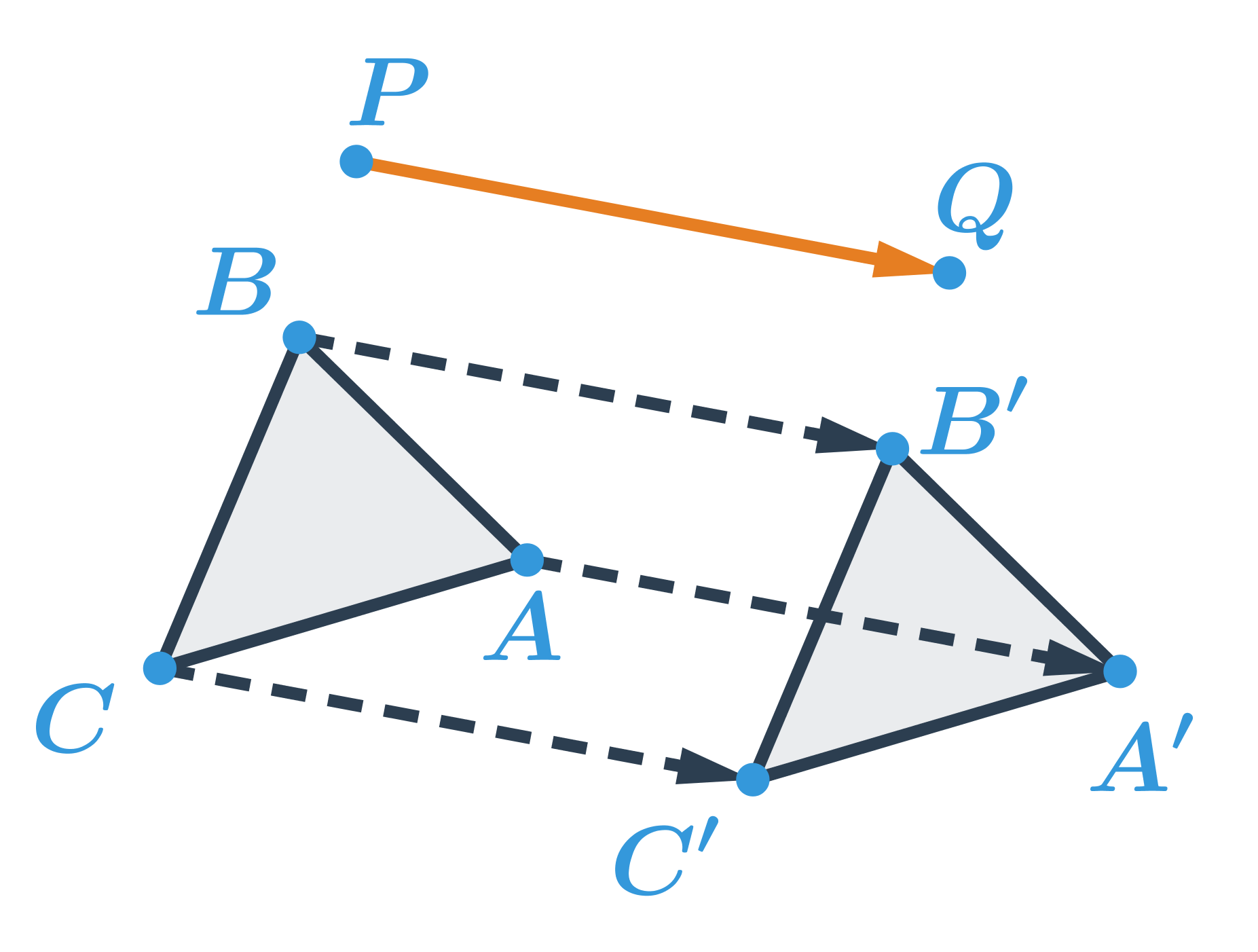
Posunutie zachováva vzdialenosti aj uhly, ide teda o druh zhodnosti.
Posunutie s použitím vektorov
Posunutie môžeme definovať ešte druhým spôsobom, ak poznáme vektory. Posunutie je potom dané vektorom posunutia \vec{u}. Obrazom bodu X je bod X', pre ktorý platí, že vektor \overrightarrow{XX'} má rovnakú veľkosť a rovnaký smer ako vektor \vec{u}.
Príklad: posunutie bodu dané vektorom
Obrazom bodu X v posunutí, ktoré je určené vektorom \vec{u}, je bod X':
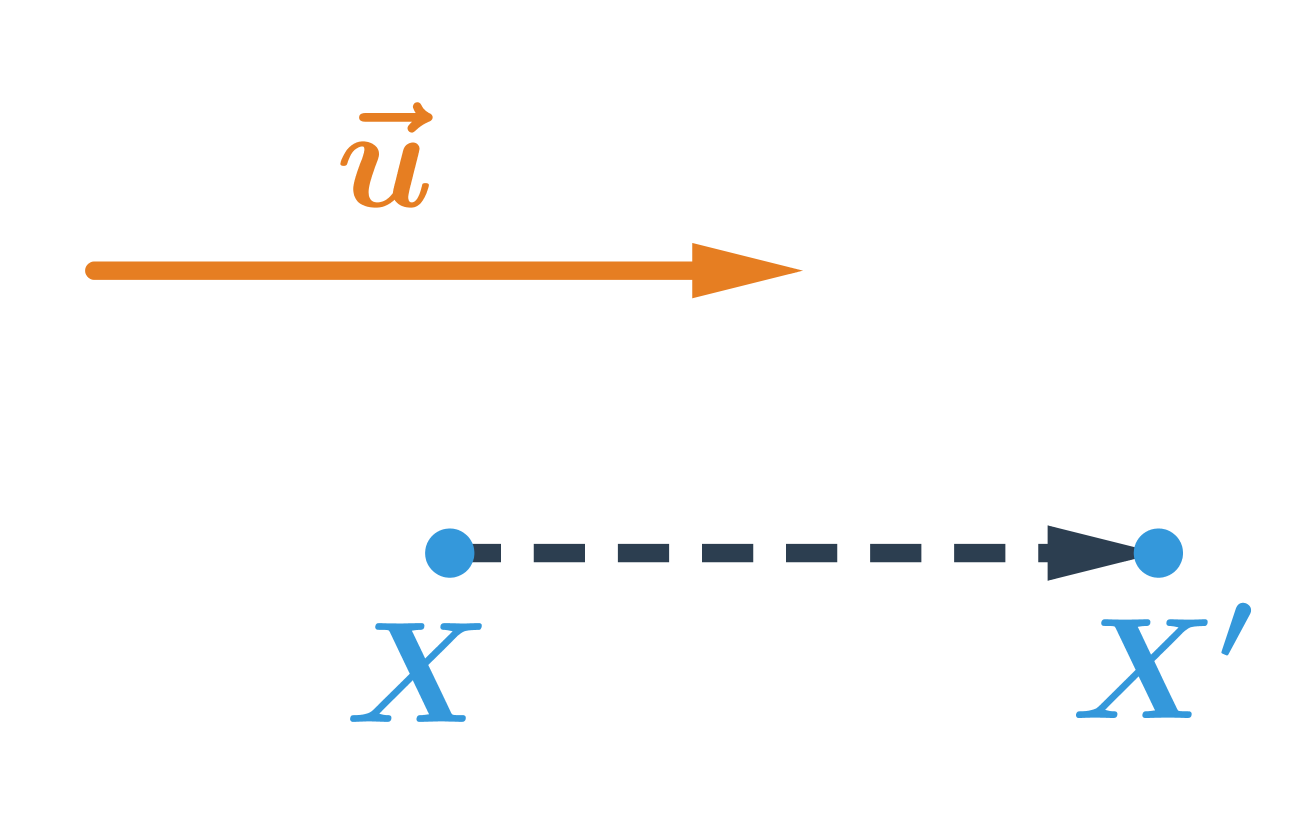
Príklad: posunutie trojuholníka dané vektorom
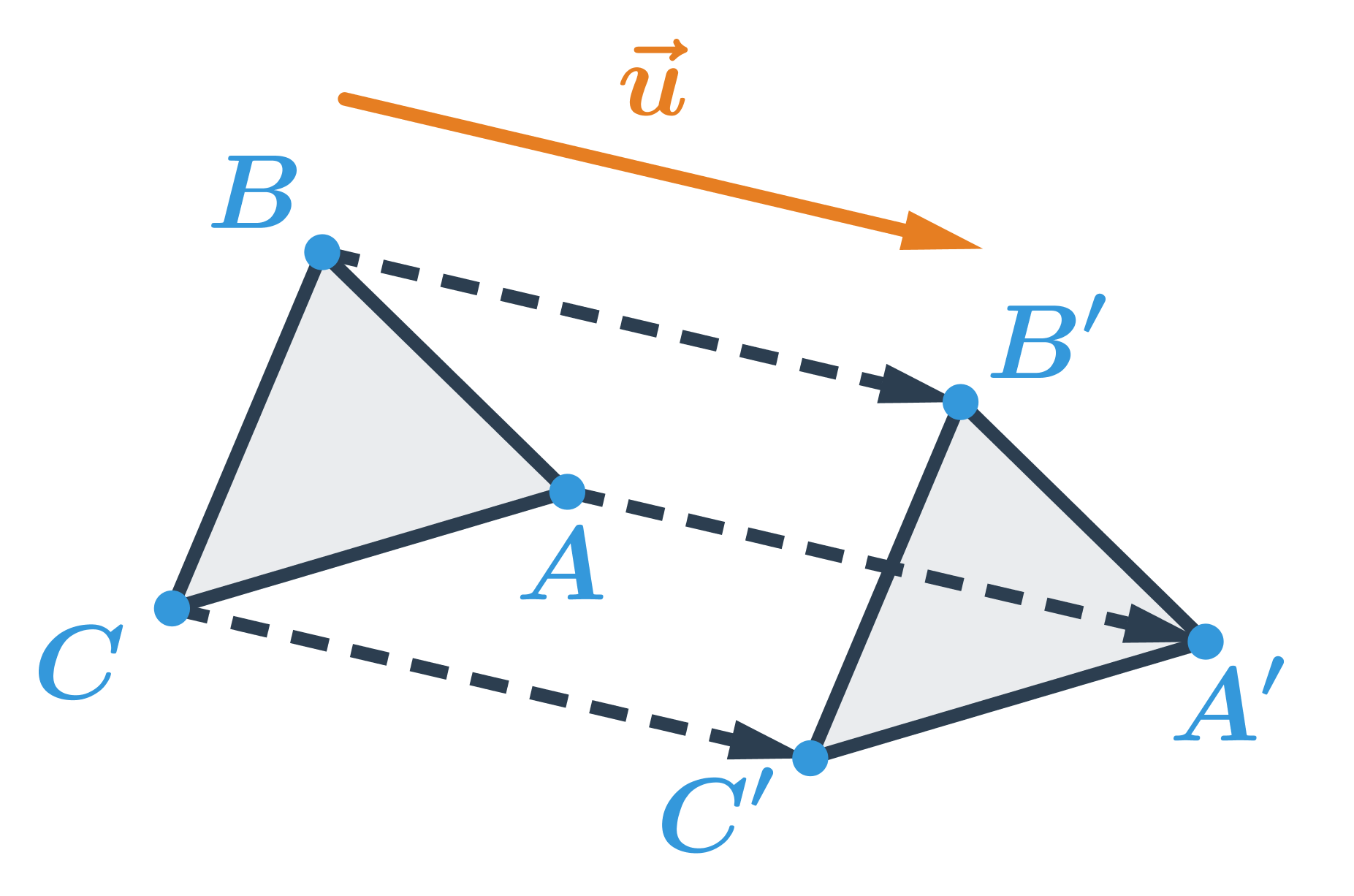
Obrazom trojuholníka ABC v posunutí, ktoré je určené vektorom \vec{u}, je trojuholník A'B'C':
Zatvoriť