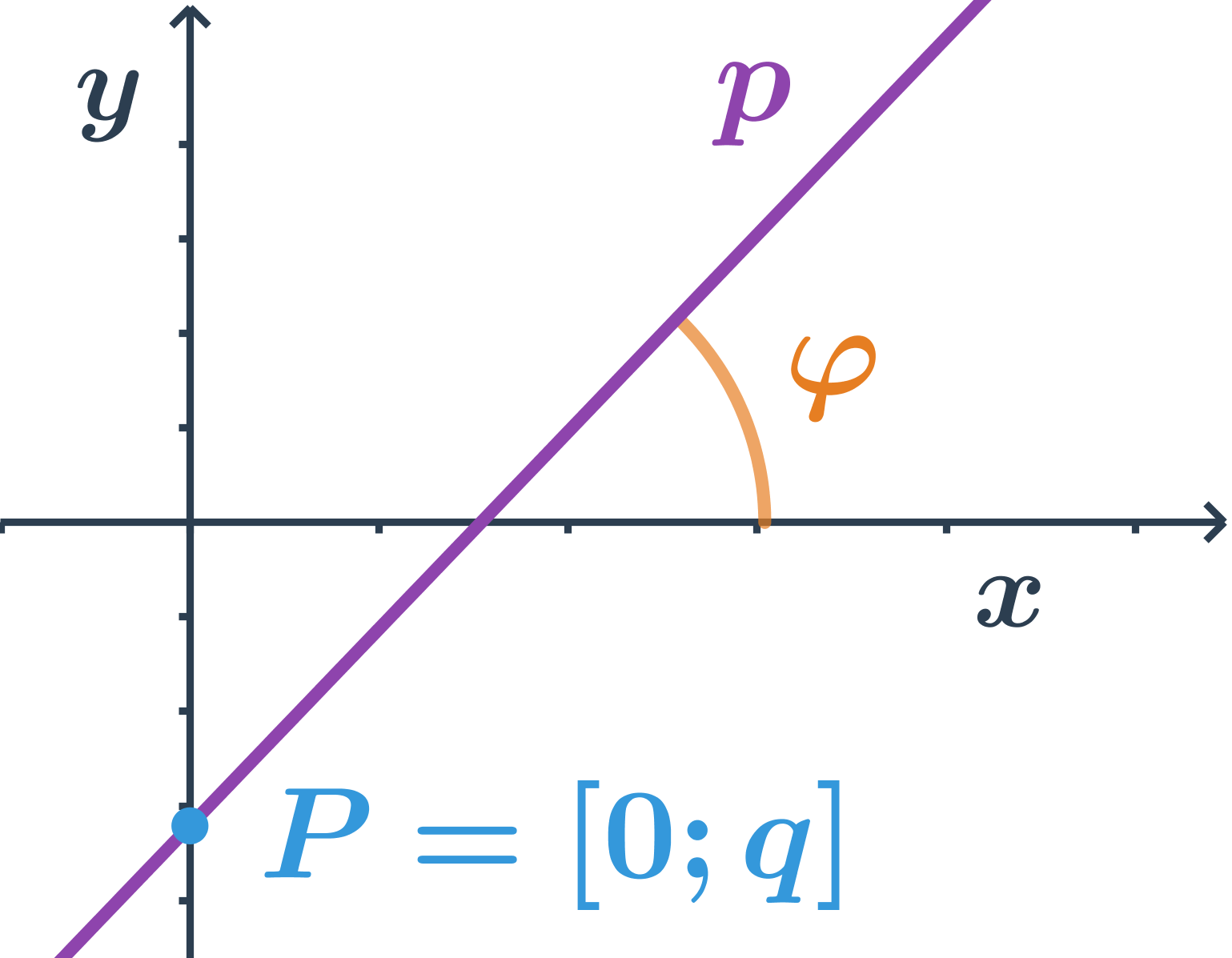Slovenčina
Angličtina
Informatika
Vieme to
Nemčina
Biológia
Zemepis
Chémia
Fyzika
Aritmetika
Zlomky, percentá, desatinné čísla
Geometria
Elementárna algebra
Funkcie
Jednotky, miery
Diskrétna matematika
Finančná gramotnosť
Rozhodovačka
Pexeso
Krok za krokom
Počítanie
Grafár
Porozumenie
Označovanie
Presúvanie
Mriežkovaná
Rozdeľovačka
Pokazená kalkulačka
Roboti
Strieľačka
Príšerky
Preteky
Územia
Tipovačka
Tímovka
Môj účet
Odhlásiť sa
Rozhodovačka
Geometria
Precvičujte neobmedzeneVáš denný počet odpovedí je obmedzený. Pre navýšenie limitu alebo prístup do svojho účtu s licenciou sa prihláste.
Prihlásiť sa
GUD
QR kód
Kód / krátka adresa
Skopírujte kliknutím.
Nastavenie cvičení
Pozor, nastavenie je platné iba pre toto cvičenie a predmet.
Smernicový tvar rovnice priamky
Každú priamku p, ktorá nie je rovnobežná s osou y môžeme vyjadriť v tvare: y=kx+q, kde k,q\in\mathbb{R}.
Tento tvar sa nazýva smernicový tvar rovnice priamky.
Konštanta k sa nazýva smernica a jej hodnota je tangens uhla, ktorý zviera priamka p s kladnou časťou osi x, teda: k=\tan \varphi.
Konštanta q určuje priesečník priamky p s osou y, súradnice priesečníka sú: P=[0;q]. Pre priamku, ktorá prechádza počiatkom je q=0, teda smernicový tvar jej rovnice je: y=kx.
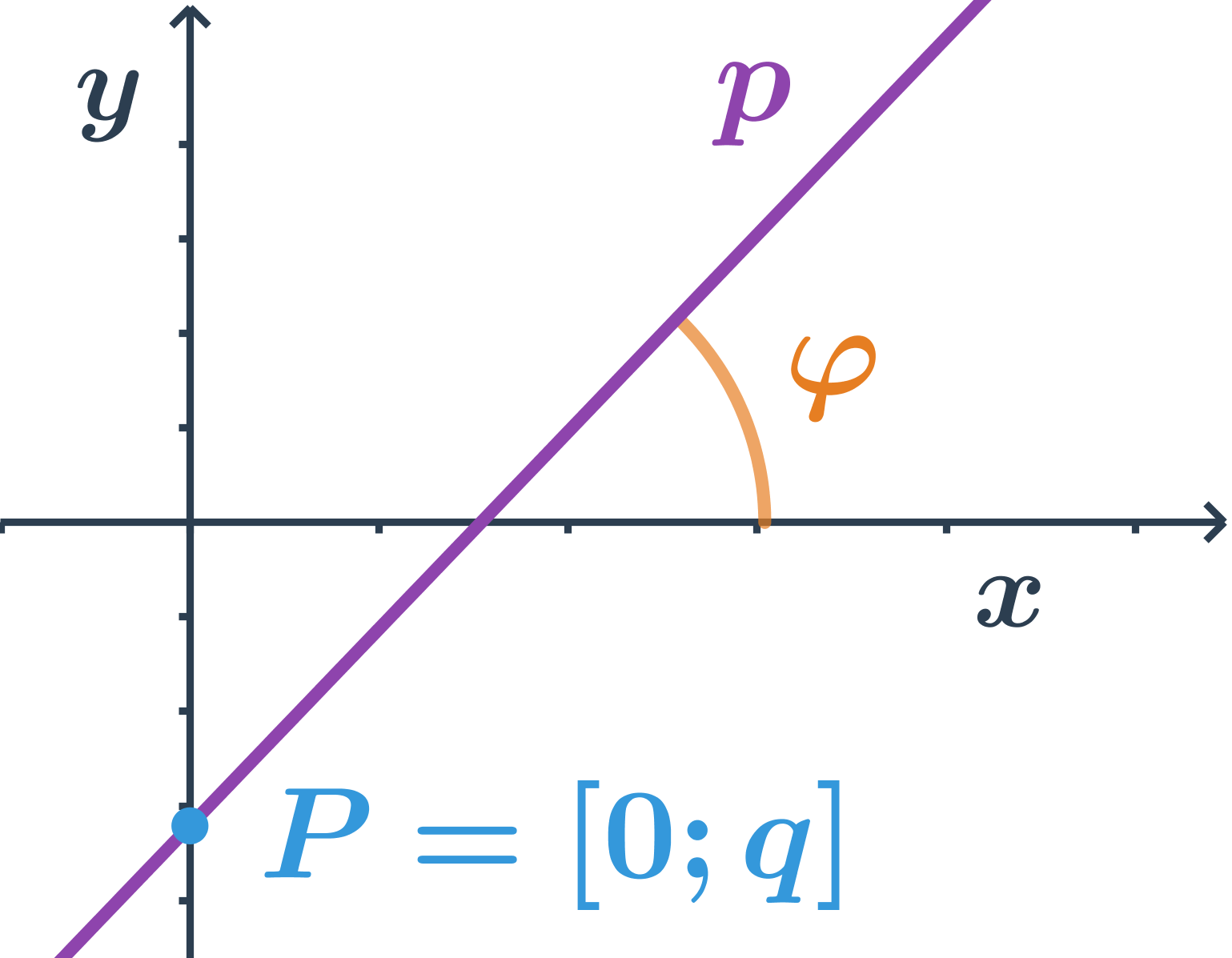
Smernica priamky, ktorá má smerový vektor \vec{u}=(u_1;u_2) je podiel súradnic smerového vektora:
k=\tan \varphi=\frac{u_2}{u_1}
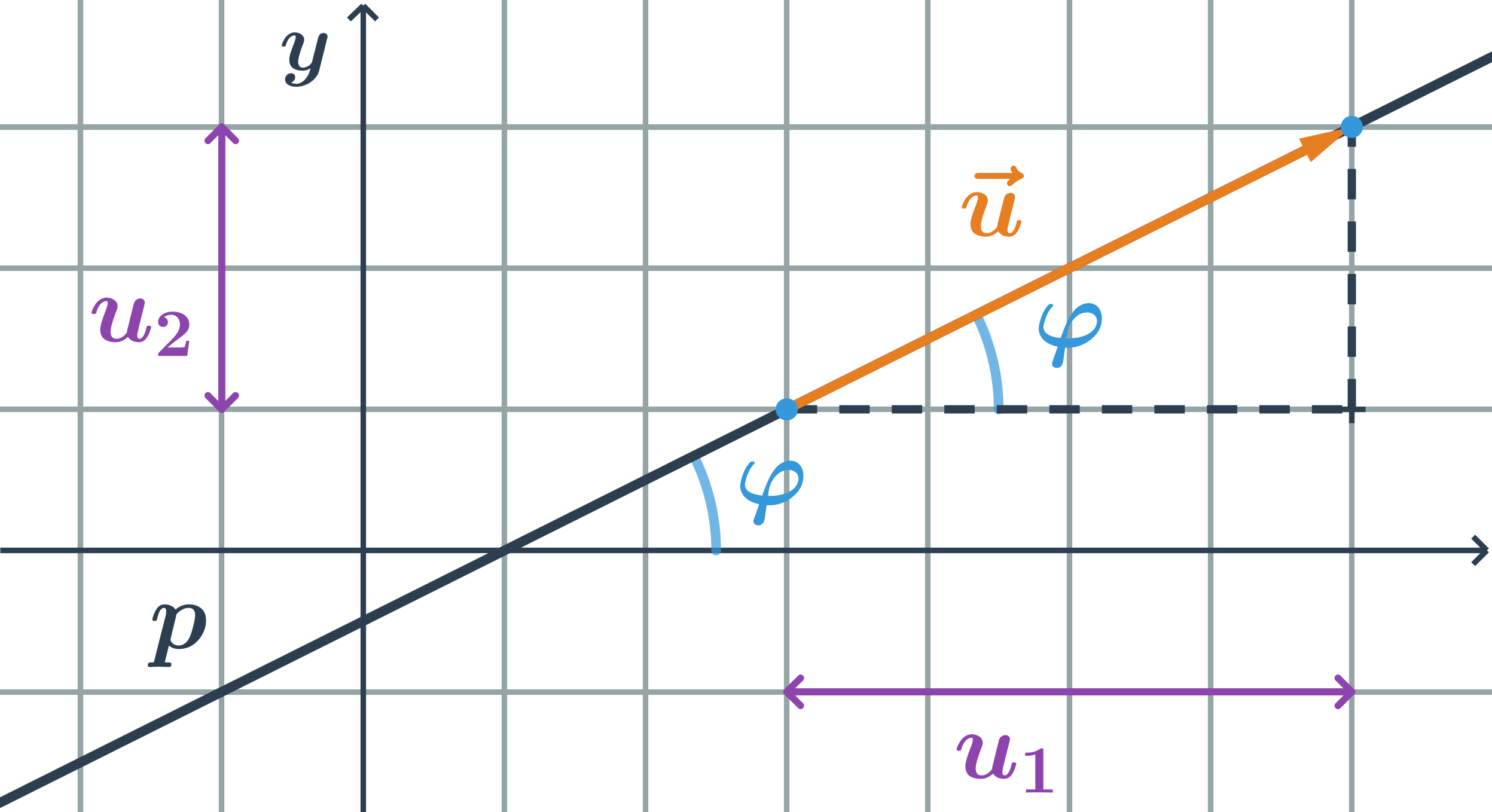
Rôzne hodnoty smernice
- Smernica priamky p: k_1=\tan \varphi_1=\frac{1}{2}
- Smernica priamky q: k_2=\tan \varphi_2=\frac{1}{1}=1
- Smernica priamky r: k_3=\tan \varphi_3=\frac{2}{1}=2
- Čím väčšia odchýlka od kladnej časti osi x, tým väčšia hodnota smernice k.
- Priamka rovnobežná s osou x zviera s kladnou časťou osi x uhol 0^\circ a teda jej smernica je \tan 0^\circ=0.
- Priamka rovnobežná s osou y zviera s kladnou časťou osi x uhol 90^\circ a pre túto hodnotu funkcie tangens nie je definovaná, preto nemôžeme určiť smernicu.
Smernicový tvar priamky z obrázka
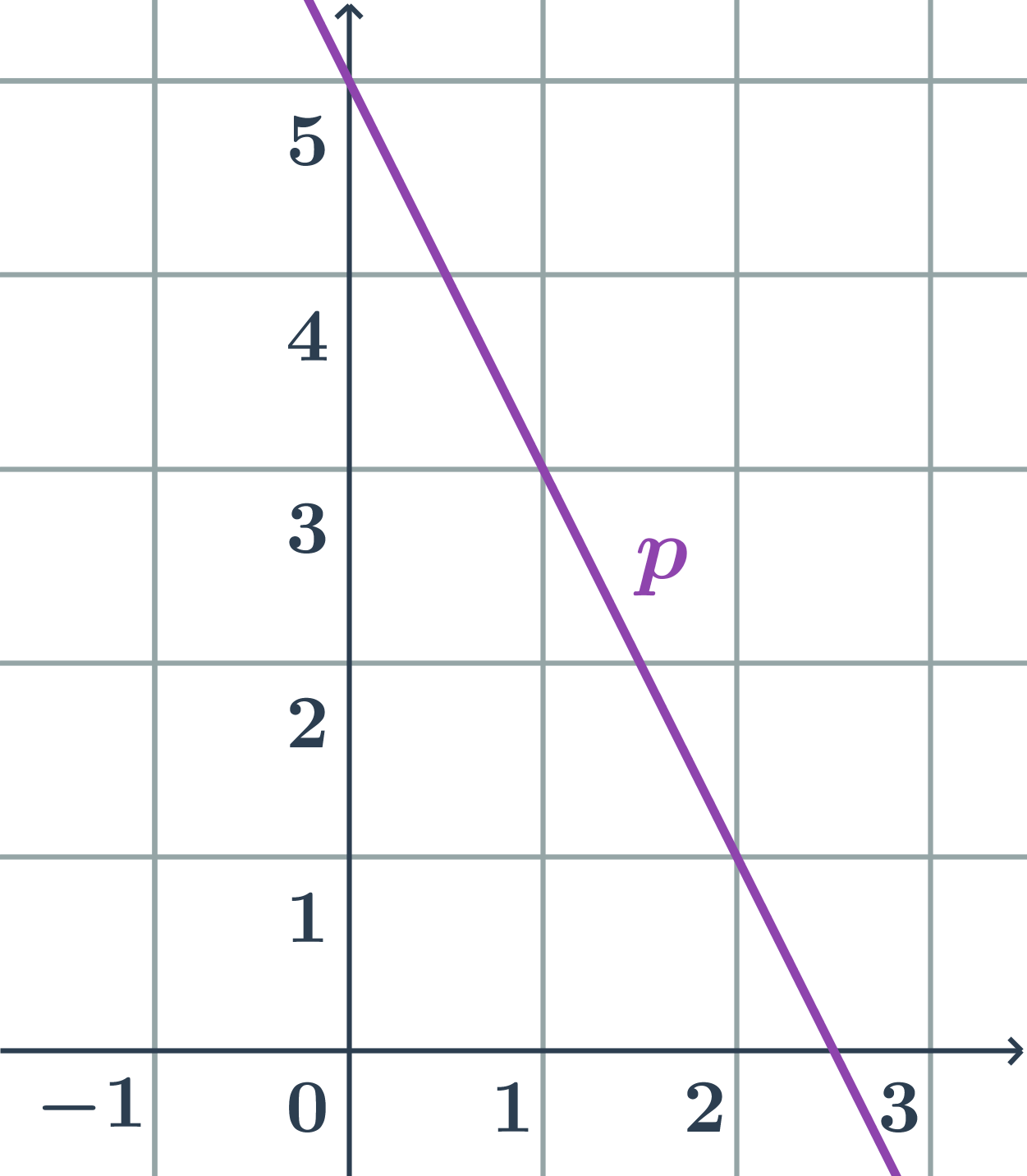
Hľadáme smernicový tvar rovnice priamky: y=kx+q.
- Pre nájdenie konštánt k a q určíme smerový vektor priamky p a priesečník s osou y.
- smerový vektor priamky: \vec{u}=(1;-2)
- smernica: k=\tan \varphi=\frac{u_2}{u_1}=\frac{-2}{1}=-2
- priesečník priamky s osou y: P=[0;5]
- konštanta q=y_P=5
- priamka na obrázku má smernicový tvar y=-2x+5
Dve priamky
Dve rovnobežné priamky zvierajú s kladnou časťou osi x rovnaký uhol, majú teda rovnakú smernicu.
Pre dve na seba kolmé priamky platí:
- priamka p má smerový vektor \vec{u}=(u_1;u_2) a teda smernicu: k=\frac{u_2}{u_1}
- každá priamka na ňu kolmá má smerový vektor (-u_2;u_1) a teda smernicu: \frac{-u_2}{u_1}=-\frac{1}{k}
Smernicový tvar rovnice priamky (stredné)
Vyriešené:
