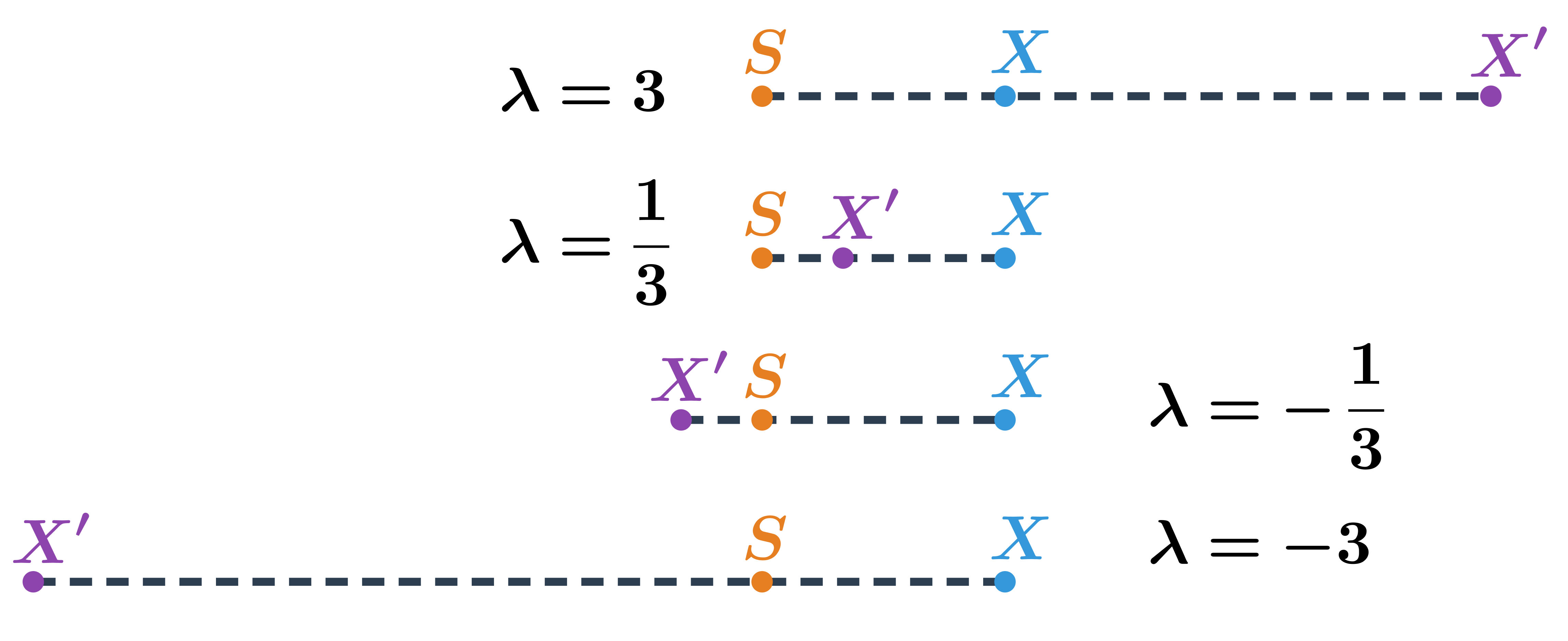Výborne, je dosiahnutý %% štít
Rovnoľahlosť » Rozhodovačka »
Rovnoľahlosť
Rozhodovačka
Precvičujte neobmedzeneVáš denný počet odpovedí je obmedzený. Pre navýšenie limitu alebo prístup do svojho účtu s licenciou sa prihláste.
Prihlásiť sa
G11
QR kód
Kód / krátka adresa
Skopírujte kliknutím.
Nastavenie cvičení
Pozor, nastavenie je platné iba pre toto cvičenie a predmet.
Rovnoľahlosť
Rovnoľahlosť je daná bodom S a nenulovým číslom \lambda. Bod S sa nazýva stred rovnoľahlosti, číslo \lambda je koeficient rovnoľahlosti.
Obrazom bodu X je bod X', pre ktorý platí:
- |SX'|=|\lambda| \cdot |SX|
- pre \lambda \gt 0 leží X, X' na rovnakej polpriamke s počiatkom S
- pre \lambda \gt 0 leží X, X' na opačných polpriamkach s počiatkom S
Na obrázku je vidieť, kde leží obraz X' bodu X v závislosti od hodnoty koeficientu \lambda:
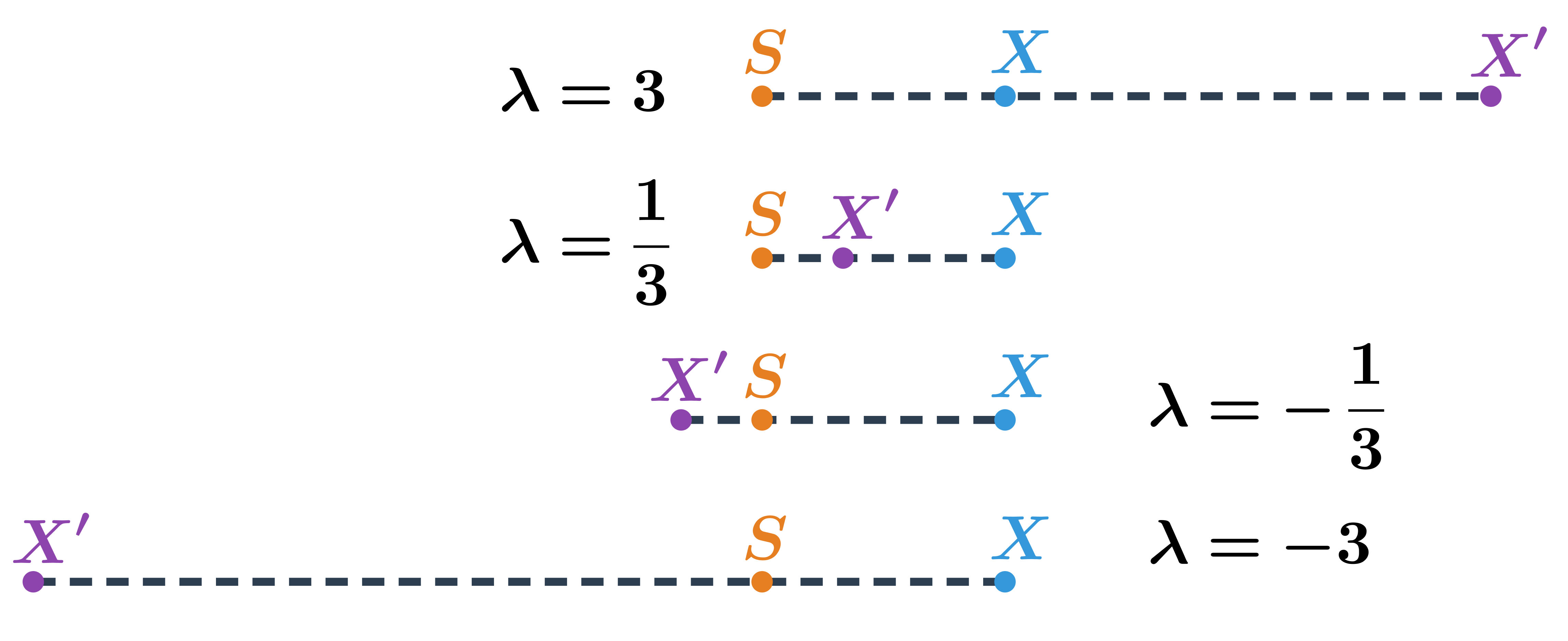
Prehľad vlastností obrazu X' bodu X v rovnoľahlosti so stredom S pre rôzne hodnoty koeficientu \lambda:
| \lambda \gt 0 | bod X' leží na polpriamke SX |
| \lambda \lt 0 | bod X' leží na polpriamke opačnej k SX |
| |\lambda| \gt 1 | bod X' má od stredu S väčšiu vzdialenosť než bod X |
| |\lambda| \lt 1 | bod X' má od stredu S menšiu vzdialenosť než bod X |
Príklad 1: obraz trojuholníka v rovnoľahlosti
Obraz trojuholníka ABC v rovnoľahlosti so stredom S a koeficientom \lambda =\frac{1}{2}
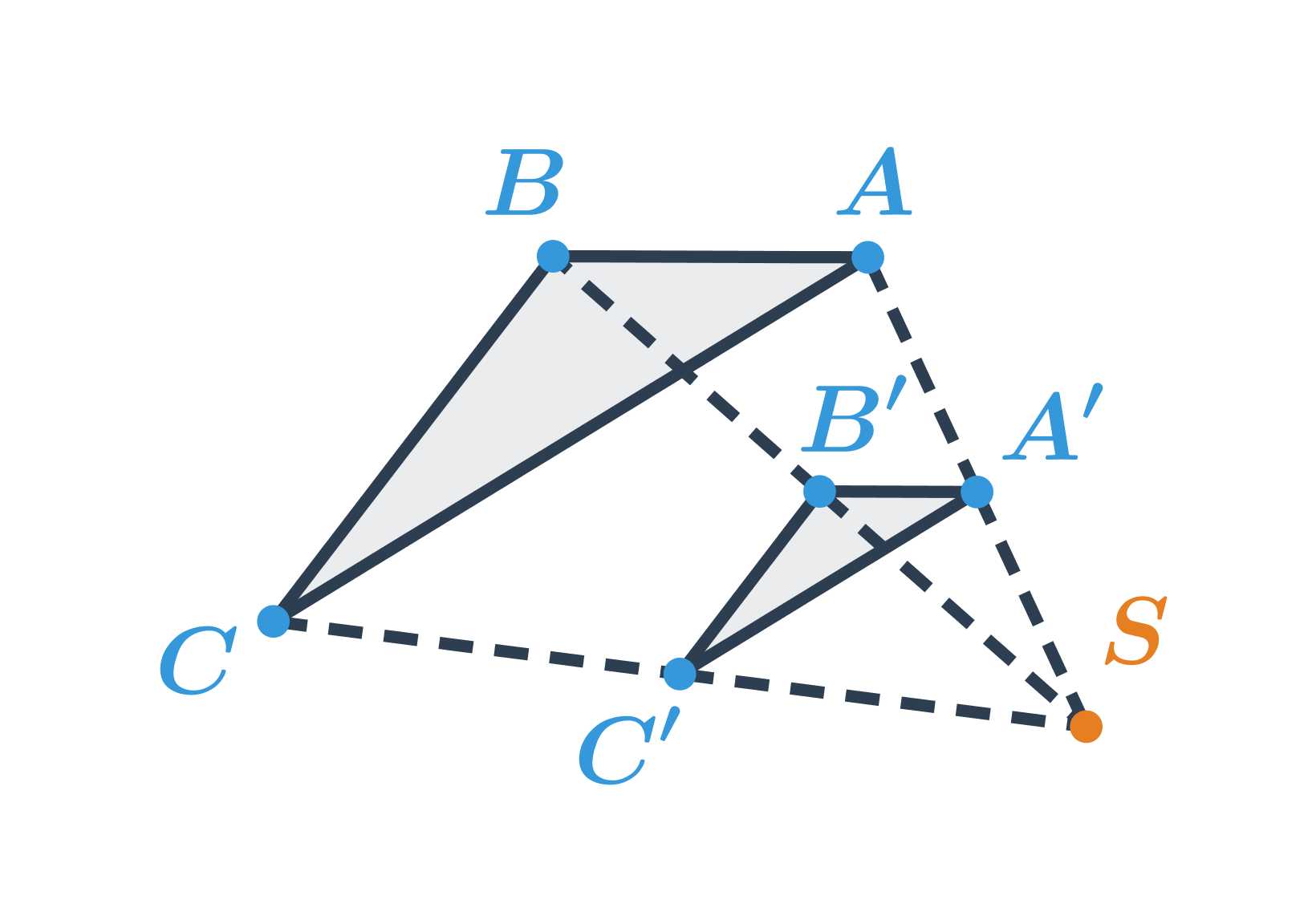
Pre dĺžky zodpovedajúcich si úsečiek platí: \frac{|SA'|} {|SA|}=\frac{|SB'|} {|SB|}=\frac{|SC'|} {|SC|}=\frac{1}{2}
Príklad 2: obraz kružnice v rovnoľahlosti
Obraz kružnice k v rovnoľahlosti so stredom S a koeficientom \lambda =-3.
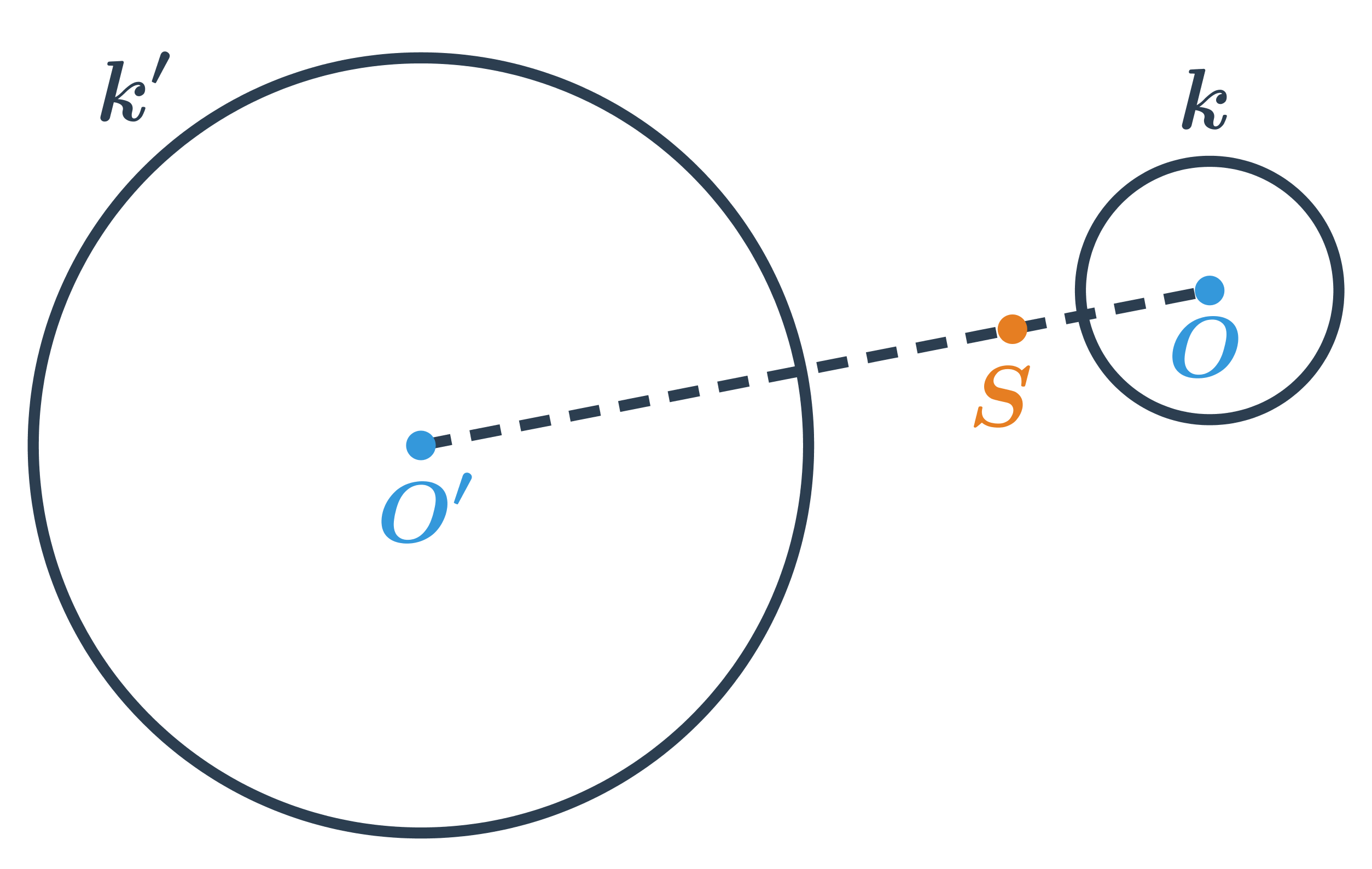
Rovnoľahlosť zachováva uhly a pomer dĺžok, ide teda o druh podobnosti.
Rovnoľahlosť (stredné)
Teraz sa už môžu opakovať už vyriešené zadania.