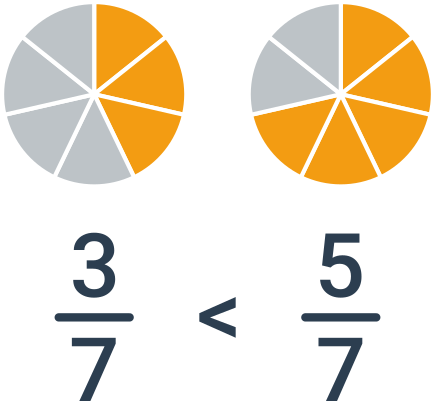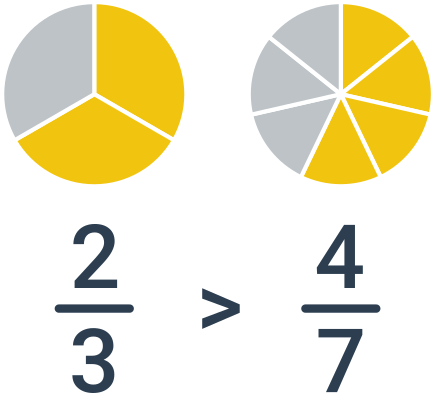Než sa pustíme do porovnávania zlomkov, je dobré mať jasno v tom, čo je čitateľ („to hore“) a menovateľ („to dole“). V zlomku \frac{3}{7} je 3 čitateľ, 7 menovateľ.

Porovnávanie zlomkov s rovnakým menovateľom

Porovnávania zlomkov s rovnakým menovateľom je jednoduché: stačí jednoducho porovnať čitatele. Ak napríklad porovnávame zlomky \frac{3}{7} a \frac{5}{7}, je väčší druhý zlomok. Oba zlomky vyjadrujú sedminy z celku a je jednoducho viac, keď máme sedmín päť.

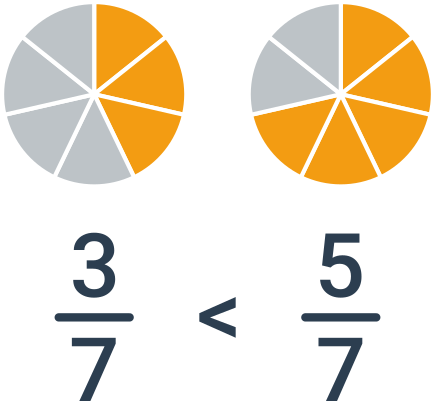
Porovnávanie zlomkov s rovnakým čitateľom

Ak majú zlomky rovnaký čitateľ, potom stačí porovnať menovatele. V tomto prípade je ale poradie zlomkov opačné než poradie menovateľov. Ak porovnávame napríklad zlomky \frac{1}{4} a \frac{1}{5}, je väčšia jedna štvrtina: dostanem väčší kúsok pizzy, ak sa bude deliť medzi 4 ľudí, než keď sa bude deliť medzi 5 ľudí.

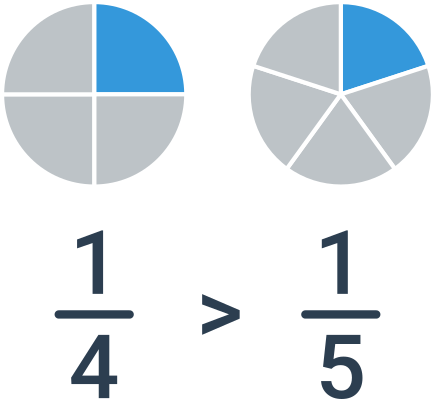
Odlišný menovateľ aj čitateľ

V tomto prípade potrebujeme zlomky najskôr previesť na spoločný menovateľ a až potom vykonať porovnanie podľa čitateľov. Príklad: porovnanie zlomkov \frac{2}{3} a \frac{4}{7}. Najmenší spoločný menovateľ je 21, po rozšírení dostávame dvojicu zlomkov \frac{2}{3}=\frac{2\cdot 7}{3\cdot 7}=\frac{14}{21} a \frac{4}{7}=\frac{4\cdot 3}{7\cdot 3}=\frac{12}{21}. Pretože 14 > 12, je väčší prvý zlomok, tj. \frac{2}{3}.

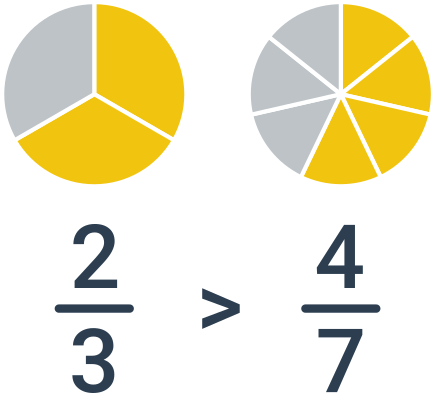
Porovnanie bez výpočtu

Často môžeme vykonať porovnanie aj bez detailného výpočtu, ak si zlomky správne predstavíme alebo porovnáme s vhodnou hodnotou „medzi“:

• Zlomky \frac{2}{3} a \frac{7}{6}. Prvý z nich je menší než 1, druhý je väčší než 1. Platí teda \frac{2}{3} < \frac{7}{6}.

• Zlomky \frac{1}{3} a \frac{4}{5}. Prvý z nich je určite menší než polovica, druhý je výrazne väčší než polovica. Platí teda \frac{1}{3} < \frac{4}{5}.