Výpis prehľadov
Goniometrické funkcie
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Goniometrické funkcie
Goniometrické funkcie (alebo tiež trigonometrické funkcie) sú funkcie, ktoré dávajú do vzťahu uhol v pravouhlom trojuholníku a pomer dvoch jeho strán. Goniometrické funkcie majú široké využitie v geometrii a veľa praktických aplikácií (napríklad v navigácii, nebeskej mechanike či geodézii). Goniometrické funkcie súvisia nie len s geometriou, ale aj s mnohými inými oblasťami matematiky. Môžeme sa s nimi stretnúť napríklad v prípade komplexných čísel či nekonečných radov.
Základné goniometrické funkcie sú sínus, kosínus a tangens. Ďalšie sú potom sekans, kosekans a kotangens.
Inverzné funkcie k funkciám goniometrickým sa nazývajú cyklometrické (napr.arkussínus, arkustangens).
HoreGoniometrické funkcie a pravouhlý trojuholník
Goniometrické funkcie môžeme v pravouhlom trojuholníku vyjadriť nasledovne:
- Sínus (\sin) uhla \alpha je pomer dĺžky odvesny protiľahlej uhlu \alpha a dĺžky prepony.
- Kosínus (\cos) uhla \alpha je pomer dĺžky odvesny priľahlej uhlu \alpha a dĺžky prepony.
- Tangens (\tan) uhla \alpha je pomer dĺžky odvesny protiľahlej uhlu \alpha a dĺžky odvesny priľahlej uhlu \alpha.
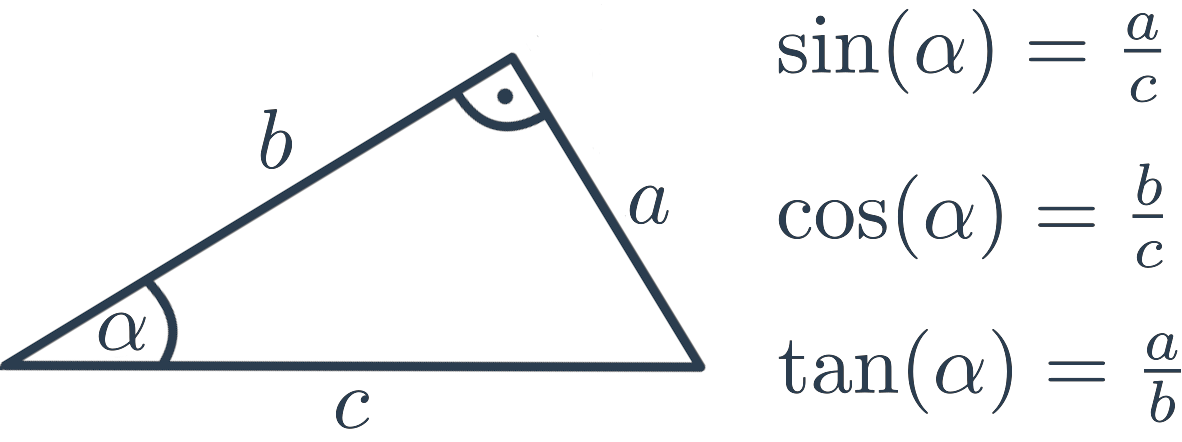
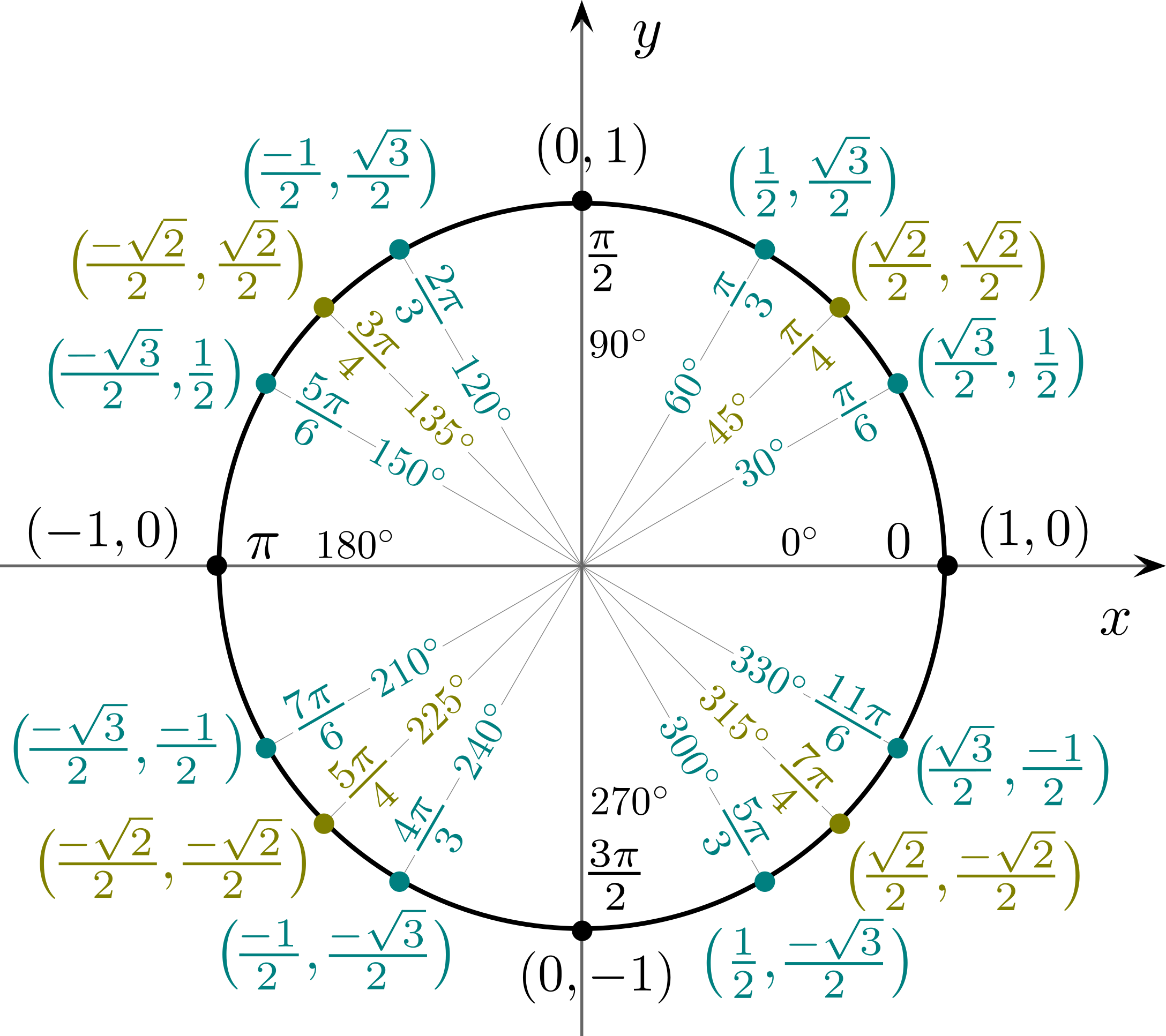
Hodnoty goniometrických funkcií
Často používané hodnoty goniometrických funkcií ilustruje tento obrázok jednotkovej kružnice – x-ová súradnica bodu zodpovedá hodnote \cos daného uhla, y-ová súradnica bodu zodpovedá hodnote \sin daného uhla.
Goniometrické funkcie: vzťahy a vzorce
Pre goniometrické funkcie platí celý rad vzťahov a vzorcov. Výber tých základných:
- Záporné hodnoty uhlov:
- \sin(-x) = -\sin(x) (nepárna funkcia)
- \cos(-x) = \cos(x) (párna funkcia)
- \tan(-x) = -\tan(x) (nepárna funkcia)
- Posuny:
- \sin(x+2\pi) = \sin(x) (perióda 2\pi)
- \sin(x+\pi) = -\sin(x)
- \sin(x+\frac{\pi}{2}) = \cos(x)
- Súčtové vzorce goniometrických funkcií:
- \sin(x+y) = \sin(x)\cos(y)+\cos(x)\sin(y)
- \sin(x-y) = \sin(x)\cos(y)-\cos(x)\sin(y)
- \cos(x+y) = \cos(x)\cos(y)-\sin(x)\sin(y)
- \cos(x-y) = \cos(x)\cos(y)+\sin(x)\sin(y)
- Dvojnásobný argument:
- \sin(2x) = 2\sin(x)\cos(x)
- \cos(2x) = \cos^2(x)-\sin^2(x)
- \tan(2x) = \frac{2\tan(x)}{1-\tan^2(x)}
Vlastnosti goniometrických funkcií
Pre obe funkcie \sin(x) a \cos(x) platí:
- definičný obor je množina reálnych čísel,
- obor hodnôt je interval \langle -1, 1 \rangle,
- funkcia je ohraničená,
- funkcia je periodická s periódou 2\pi,
- funkcia nie je prostá.
Pre funkciu \sin(x) platí:
- je nepárna,
- nulové hodnoty nadobúda v bodoch x=k\pi.
Pre funkciu \cos(x) platí:
- je párna,
- nulové hodnoty nadobúda v bodoch x=(2k+1)\frac{\pi}{2}.
Pre funkciu \tan(x) platí:
- definičný obor je \{x \in \mathbb{R}: x \neq (2k+1)\frac{\pi}{2} \},
- obor hodnôt je množina reálnych čísel,
- funkcia je nepárna,
- funkcia je periodická s periódou \pi,
- funkcia je ohraničená,
- nulové hodnoty nadobúda v bodoch x=k\pi.

