Výpis prehľadov
Objem a povrch
Podkapitoly
Objem a povrch
Objem telesa vyjadruje, koľko miesta v priestore teleso zaberá. Môžeme si ho predstaviť ako množstvo vody, ktoré by sme potrebovali, keby sme chceli teleso „napustiť“. Na vyjadrenie objemu využívame jednotky objemu.
Povrch telesa je súčet obsahov všetkých plôch, ktoré teleso ohraničujú. Môžeme si ho predstaviť ako veľkosť farebného papiera, ktorý potrebujeme na „polepenie“ telesa. Na vyjadrenie povrchu využívame jednotky obsahu.
Značenie vo vzorcoch
| V | objem |
| S | povrch |
| S_p | obsah podstavy |
| S_{pl} | obsah plášťa |
| a, b, c | dĺžky strán |
| r | polomer |
| v | výška |
| s | strana kužeľa |
Vzorce
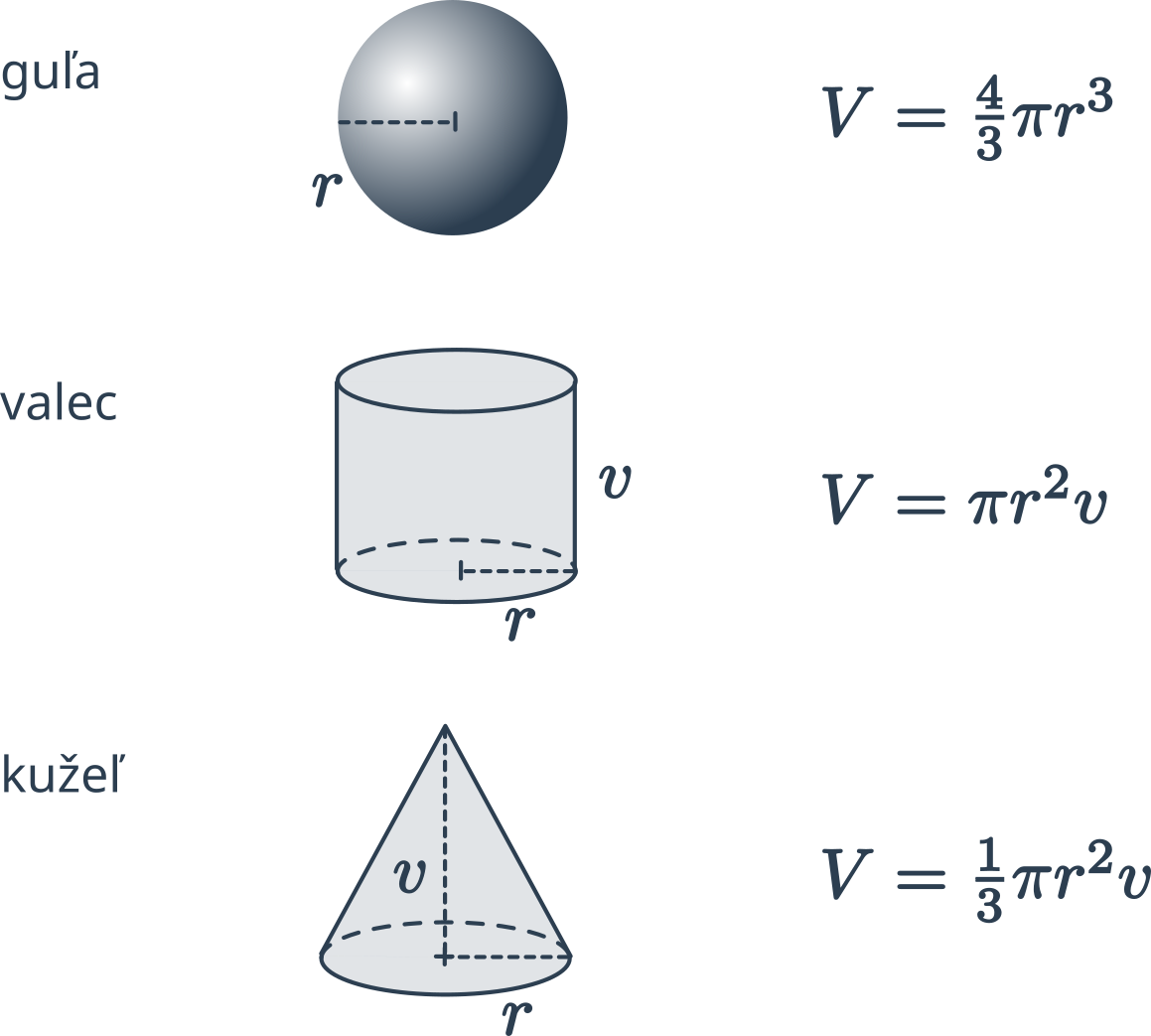
| Útvar | Objem | Povrch | |
|---|---|---|---|
| kocka | V = a^3 | S=6a^2 | |
| kváder | V = abc | S = 2(ab+ac+bc) | |
| guľa | V=\frac43\pi r^3 | S=4\pi r^2 | |
| valec | V=S_p\cdot v =\pi r^2 v | S=2S_p+S_{pl} =2\pi r(r+v) | |
| kužeľ | V=\frac{1}{3}S_p\cdot v =\frac13 \pi r^2 v | S =S_p+S_{pl} =\pi r(r+\sqrt{r^2+v^2})=\pi r^2 +\pi rs | |
| ihlan | V=\frac{1}{3}S_p\cdot v | S=S_p+S_{pl} | |
| pravidelný štvorboký ihlan | V=\frac{1}{3}S_p\cdot v=\frac{1}{3} a^2v | ||
| hranol | V= S_p\cdot v | S=2\cdot S_p+S_{pl} |
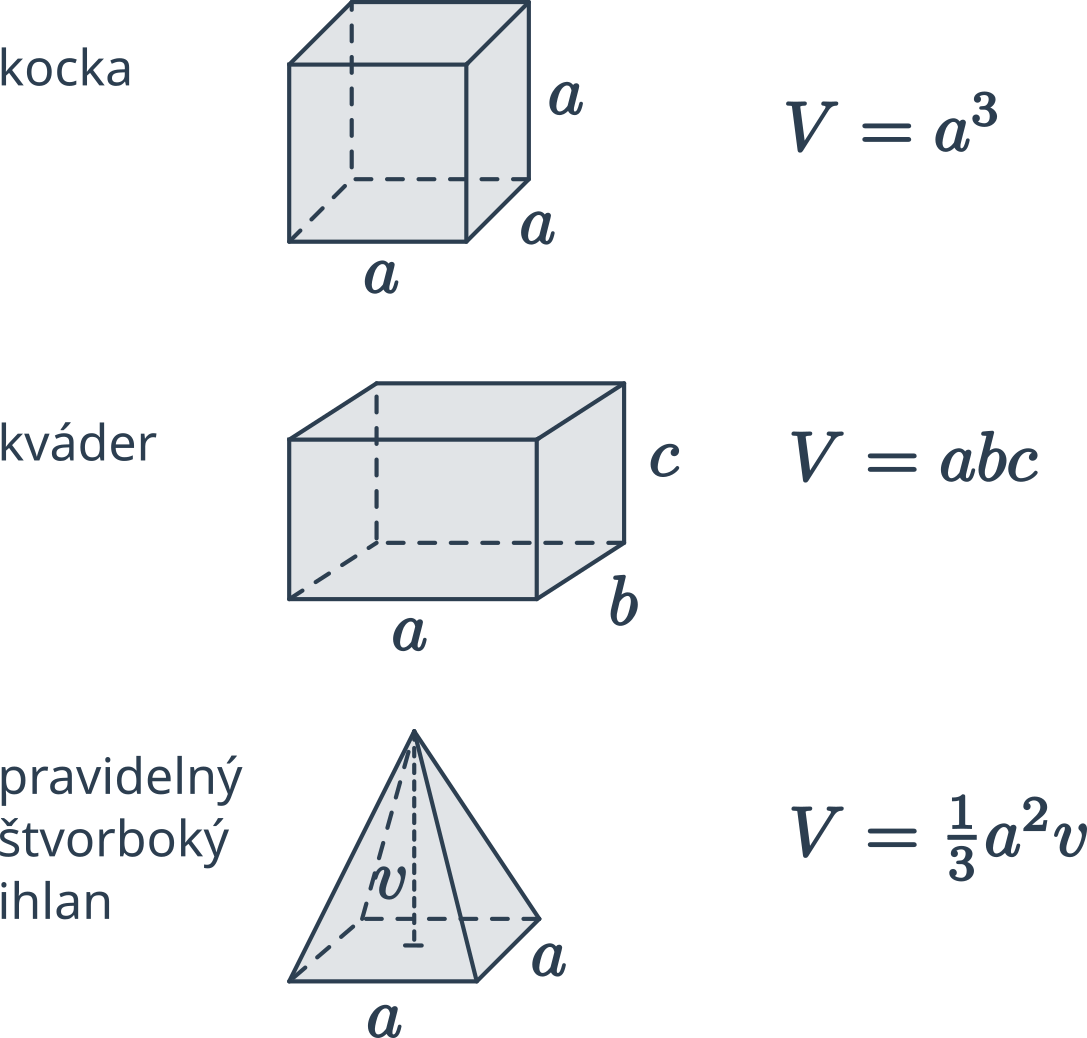
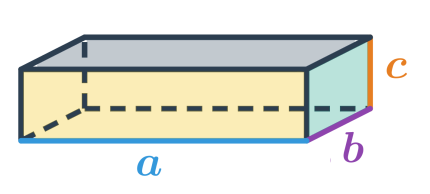
Objem kocky a kvádra
Objem kvádra s dĺžkami hrán a,b,c je: V=a\cdot b\cdot c
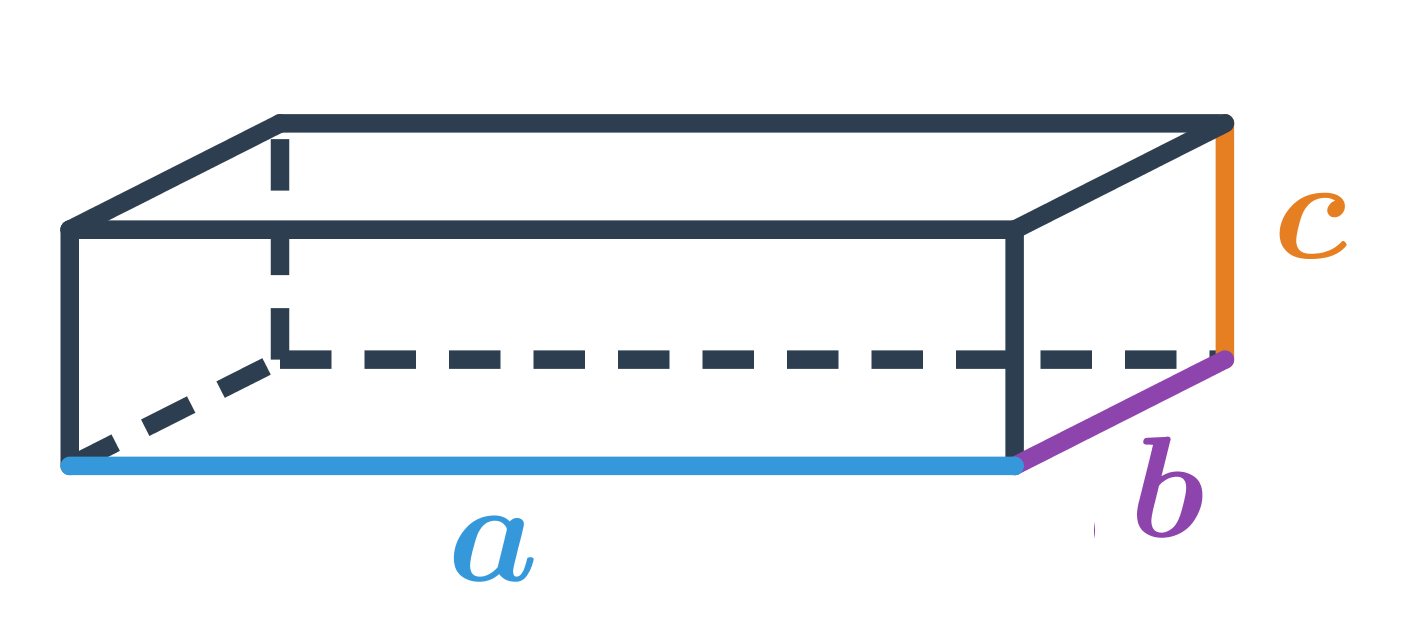
Objem kocky s dĺžkou hrany podstavy a vypočítame rovnakým spôsobom, ako objem kvádra s a=b=c, tedy: V=a\cdot a\cdot a=a^3
HoreObjem hranola
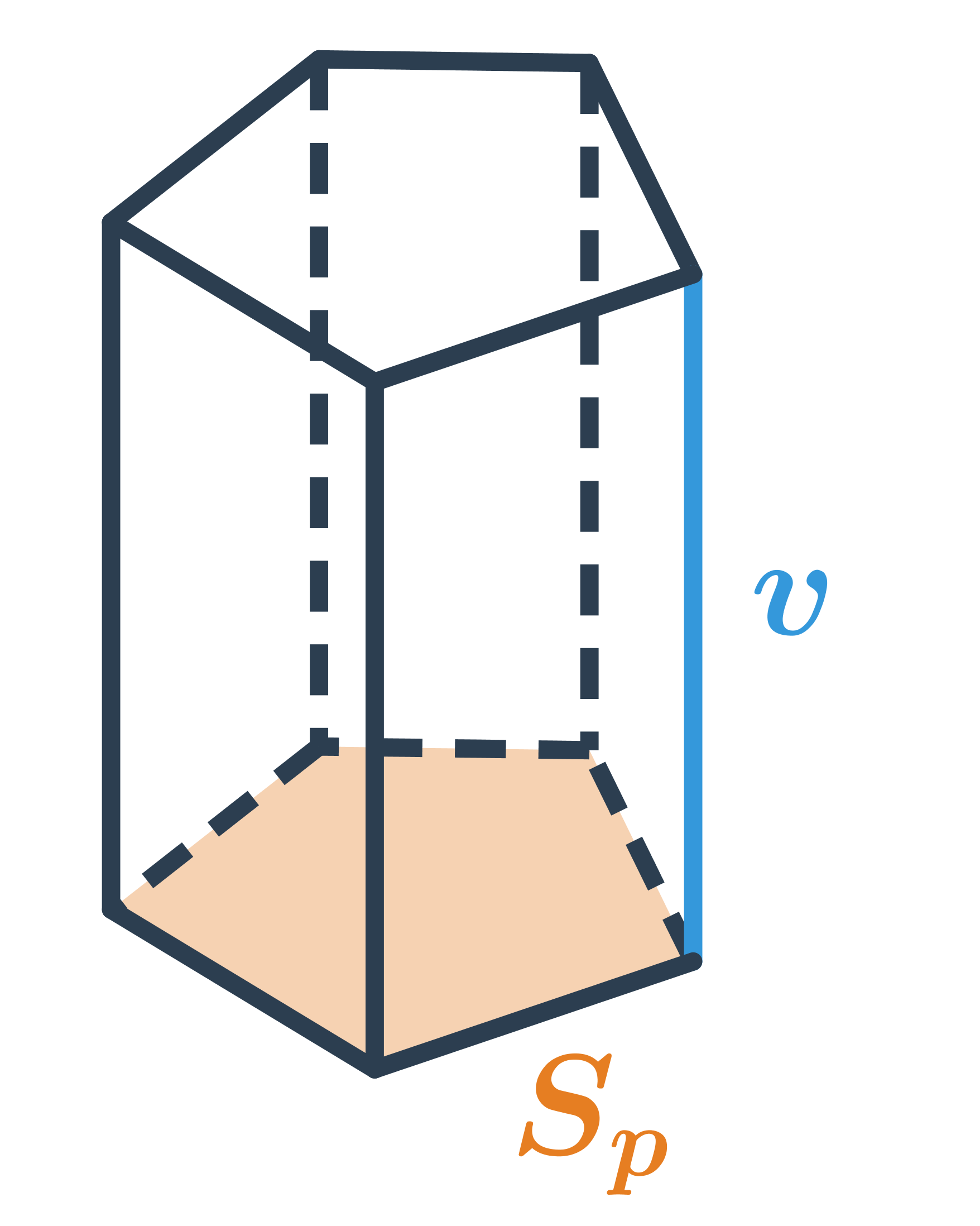
Objem hranola, ktorý má podstavu s obsahom S_p a výšku v, spočítame ako V=S_p \cdot v.
Objem ihlanu
Objem ihlanu, ktorý má podstavu s obsahom S_p a výšku v, vypočítame ako V=\frac{1}{3} S_p \cdot v.
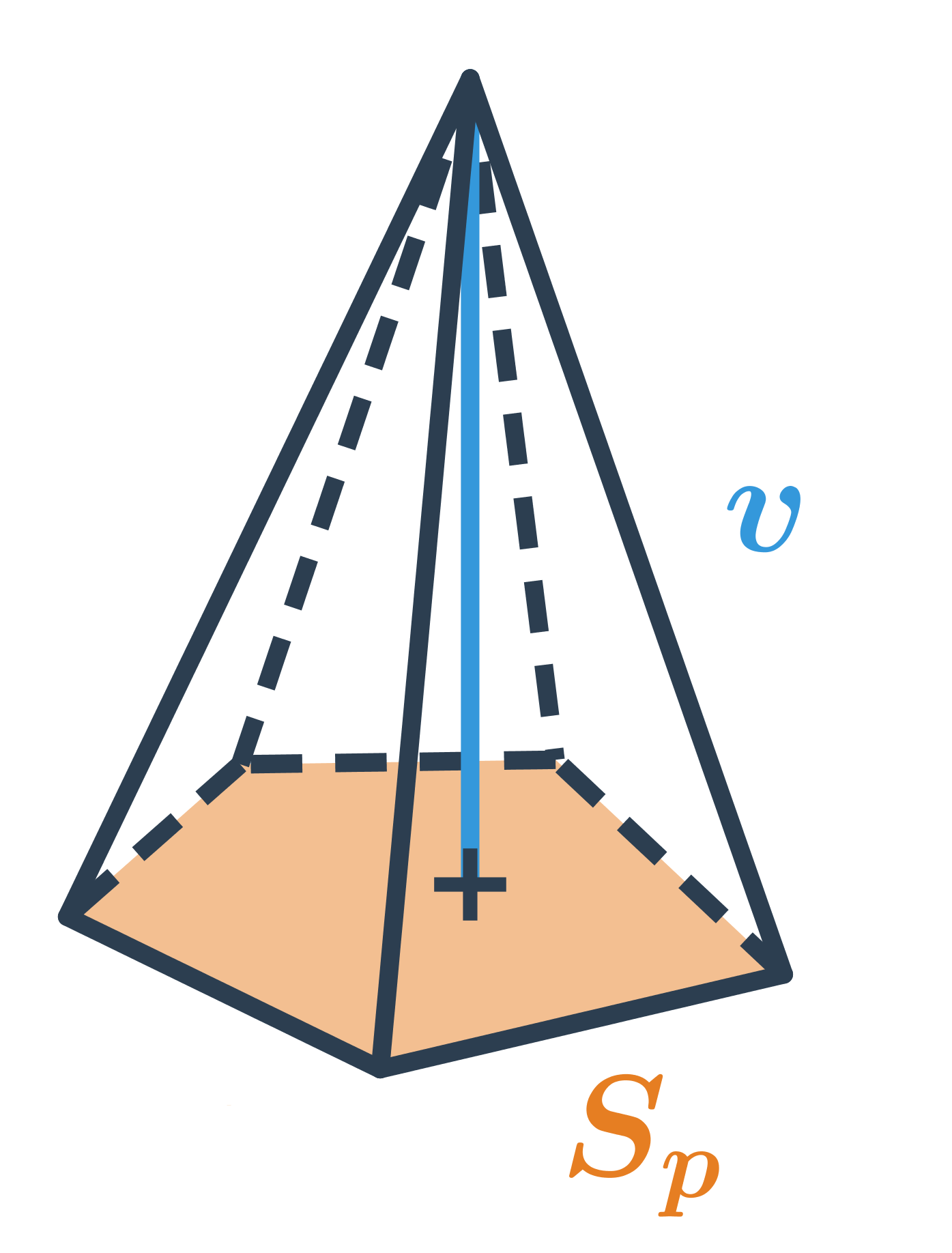
Oproti hranolu s rovnakou výškou a tvarom podstavy má ihlan trikrát menší objem.
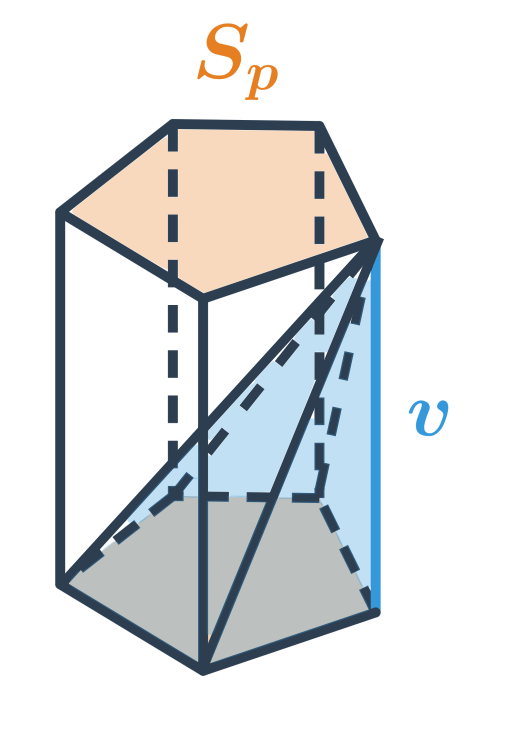
Objem hranatých telies
Vzorce pre objem „hranatých“ telies vychádzajú z obsahu podstavy a výšky telesa.
Objem ľubovoľného hranola je súčin obsahu podstavy a výšky: V=S_p\cdot v.
Kváder a kocka sú špeciálne prípady hranola, ktorých podstava je obdĺžnik (štvorec) a výška je zvyšná hrana. Objem kvádra je teda súčin dĺžok jeho hrán: V = abc. Objem kocky vypočítame rovnakým spôsobom. Keďže sú v kocke všetky hrany rovnako dlhé, výraz sa zjednoduší na V = a^3.
Objem ihlanu je jedna tretina súčinu obsahu podstavy a výšky, teda V=\frac{1}{3}S_p\cdot v. Pre pravidelný štvorboký ihlan potom teda V=\frac{1}{3} a^2v.
Príklady:
- Kocka s hranou 4 m má objem V = 4^3 = 64 m³.
- Kváder s hranami 3, 6 a 10 cm má objem V = 3\cdot 6 \cdot 10 = 180 cm³.
- Pravidelný štvorboký ihlan s podstavou s hranou 6 cm a výškou 4 cm má objem V=\frac{1}{3} 6^2 \cdot 4 = 48 cm³.
Objem valca
Objem valca s polomerom podstavy r a výškou v vypočítame ako: V=\pi \cdot r^2 \cdot v
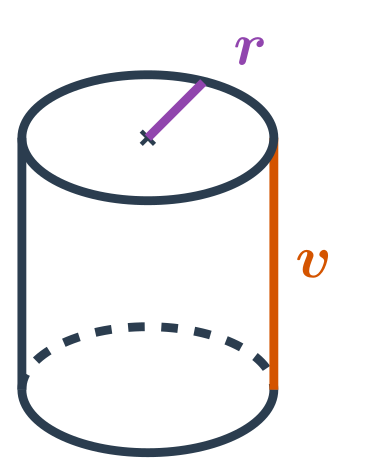
Platí V=S_p \cdot v, kde S_p je obsah podstavy valca. Podstava valca má tvar kruhu s polomerom r, takže máme: S_p = \pi \cdot r^2
HoreObjem kužeľa
Objem kužeľa s polomerom podstavy r a výškou v vypočítame ako: V=\frac{1}{3} \pi \cdot r^2 \cdot v
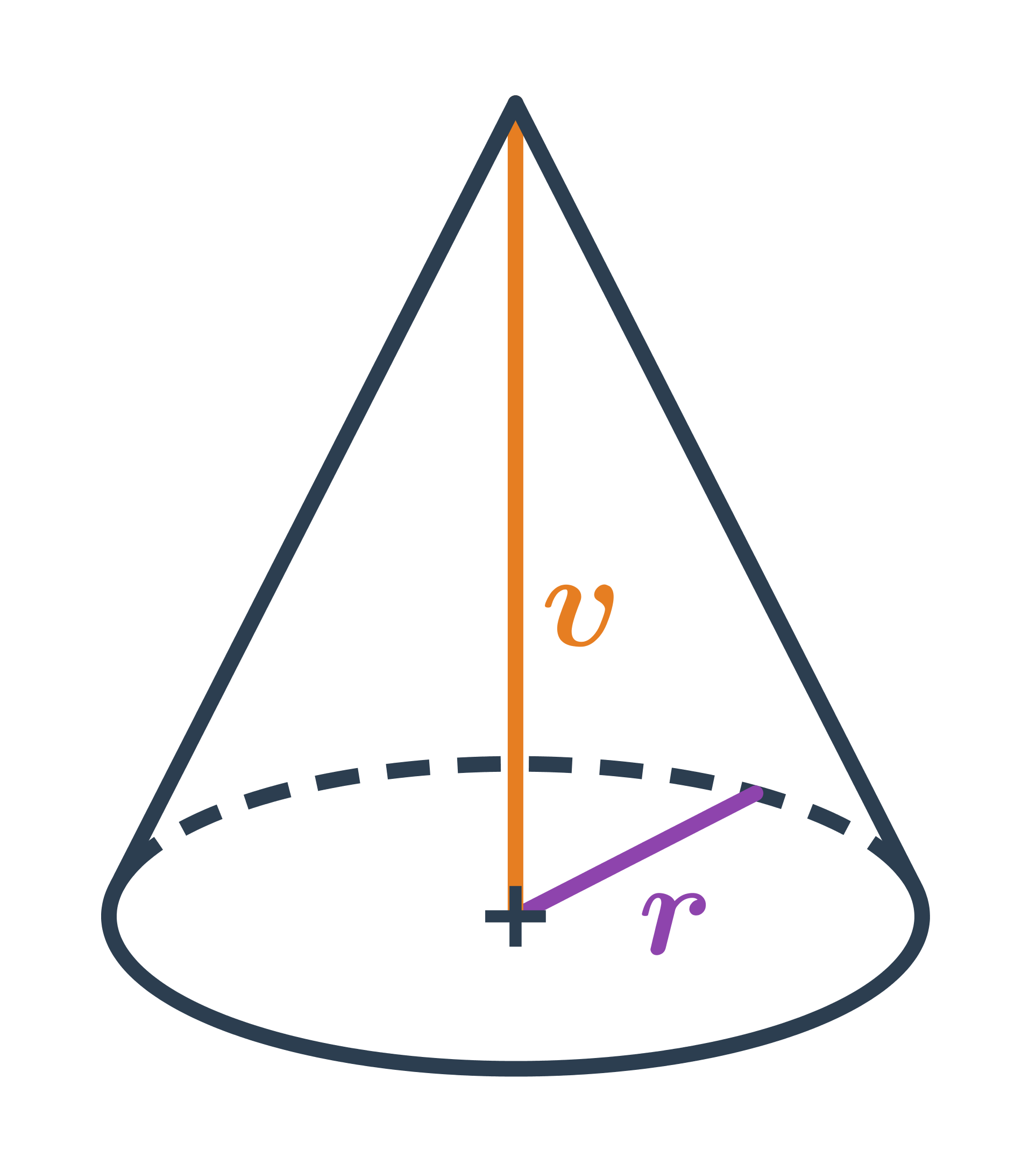
Pre kužeľ platí V=\frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy valca. Podstava valca má tvar kruhu s polomerom r, takže máme: S_p = \pi \cdot r^2
Oproti valcu s rovnakou výškou a polomerom podstavy má kužeľ trikrát menší objem.
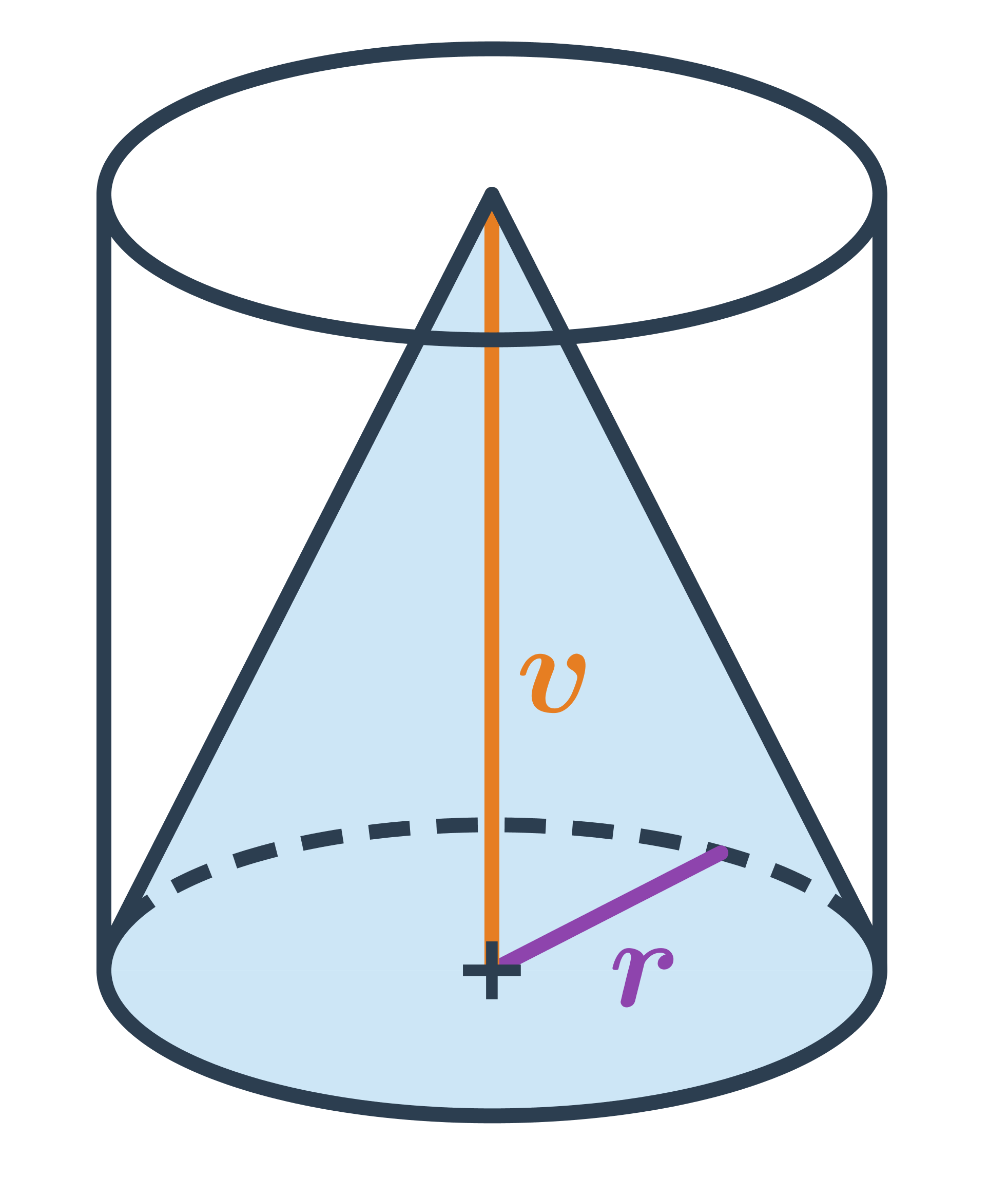
Objem okrúhlych telies
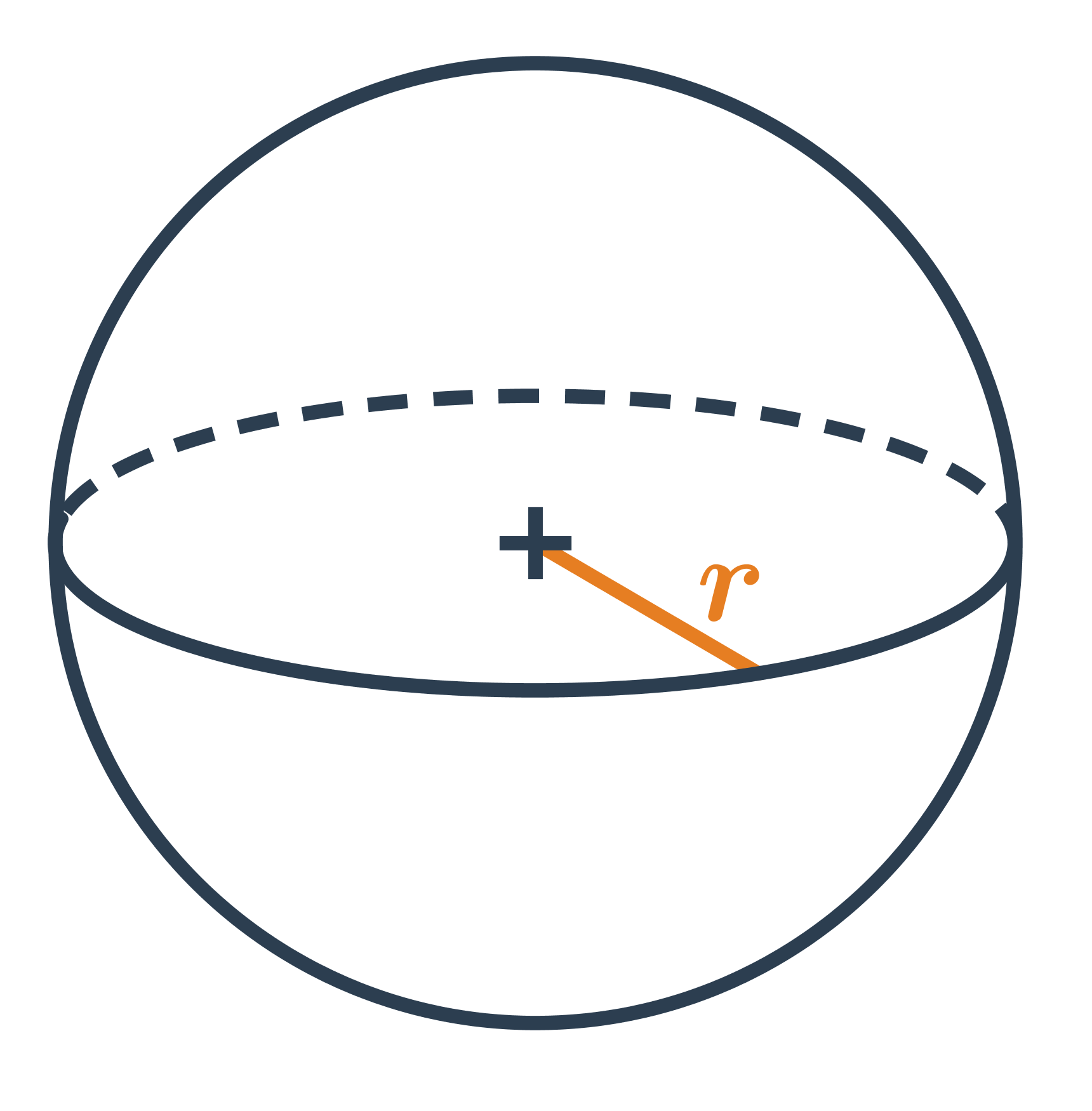
Objem „guľatých“ telies vypočítame s využitím konštanty \pi \approx 3{,}14 159 265. Vo vzorcoch označuje r polomer (gule či podstavy) a v výšku valca.
- Objem gule je V = \frac43 \pi r^3.
- Objem valca je obsah (kruhovej) podstavy vynásobený výškou, teda V = S_p \cdot v = \pi r^2 v.
- Objem kužeľa je jedna tretina obsahu podstavy vynásobeného výškou, teda V = \frac13 S_p \cdot v = \frac13 \pi r^2 v.
Povrch kocky a kvádra
Povrch kvádra s dĺžkami hrán a,b,c vypočítame ako súčet obsahov všetkých jeho stien. Teda: S=2 (a\cdot b + a\cdot c + b \cdot c)
Povrch kocky s dĺžkou hrany podstavy a vypočítame rovnakým spôsobom ako objem kvádra s a=b=c, teda šesťkrát obsah jednej štvorcovej steny kocky: S = 6\cdot a\cdot a = 6a^2
HorePovrch hranola
Povrch hranola, ktorý má podstavu s obsahom S_p a plášť s obsahom S_{pl}, vypočítame ako S=2S_p + S_{pl}. Plášť hranola je tvorený všetkými jeho stenami okrem dvoch podstáv.
Povrch pravidelného n‑bokého hranola, ktorý má dve podstavy v tvare pravidelných n‑uholníkov a potom n rovnakých obdĺžnikových stien (obsah jednej označme S_1), vypočítame takto: S=2S_p + n\cdot S_1
HorePovrch ihlanu
Povrch ihlanu vypočítame ako súčet obsahu jeho podstavy S_p a obsahu jeho plášťa S_{pl}. Obsah plášťa vypočítame ako súčet obsahov stien ihlanu, ktoré tvoria plášť (teda všetky steny ihlanu okrem jeho podstavy).
Povrch pravidelného n‑bokého ihlanu, ktorý má podstavu v tvare pravidelného n‑uholníka a potom n rovnakých trojuholníkových stien (obsah jednej označme S_1), vypočítame takto: S= S_p + n\cdot S_1
HorePovrch hranatých telies
Povrch „hranatých“ telies je jednoducho súčet obsahov jednotlivých strán.
Hranol má dve rovnaké podstavy a plášť, povrch je teda S=2\cdot S_p+S_{pl}. Ihlan má jednu podstavu a plášť, povrch je teda S=S_p+S_{pl}.
Steny kvádra sú obdĺžniky, pričom sú vždy dve rovnako veľké. Povrch teda vypočítame ako S = 2(ab+ac+bc).
Kocka má šesť stien a všetky sú tvorené rovnakým štvorcom. Povrch je S=6a^2.
Povrch valca
Povrch valca s polomerom podstavy r a výškou v vypočítame ako: S = 2\pi r \cdot(r + v)
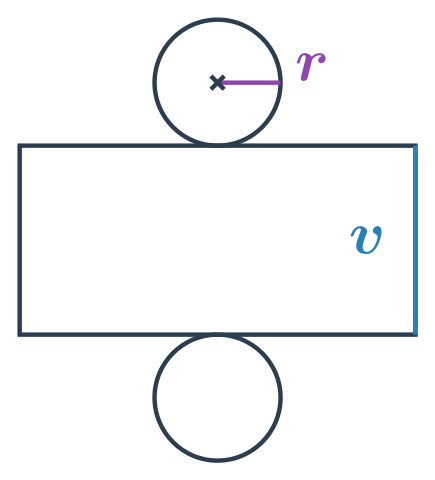
Platí S=2S_p + S_{pl}, kde S_p je obsah podstavy valca a S_{pl} obsah plášťa valca. Podstava valca má tvar kruhu s polomerom r a plášť valca je obdĺžnik so stranami v a 2\pi r. Celkovo máme:
- Obsah podstavy: S_p = \pi \cdot r^2
- Obsah plášťa: S_{pl}=2\pi r \cdot v
- Povrch valca: S=2\pi r \cdot (r + v)
Povrch kužeľa
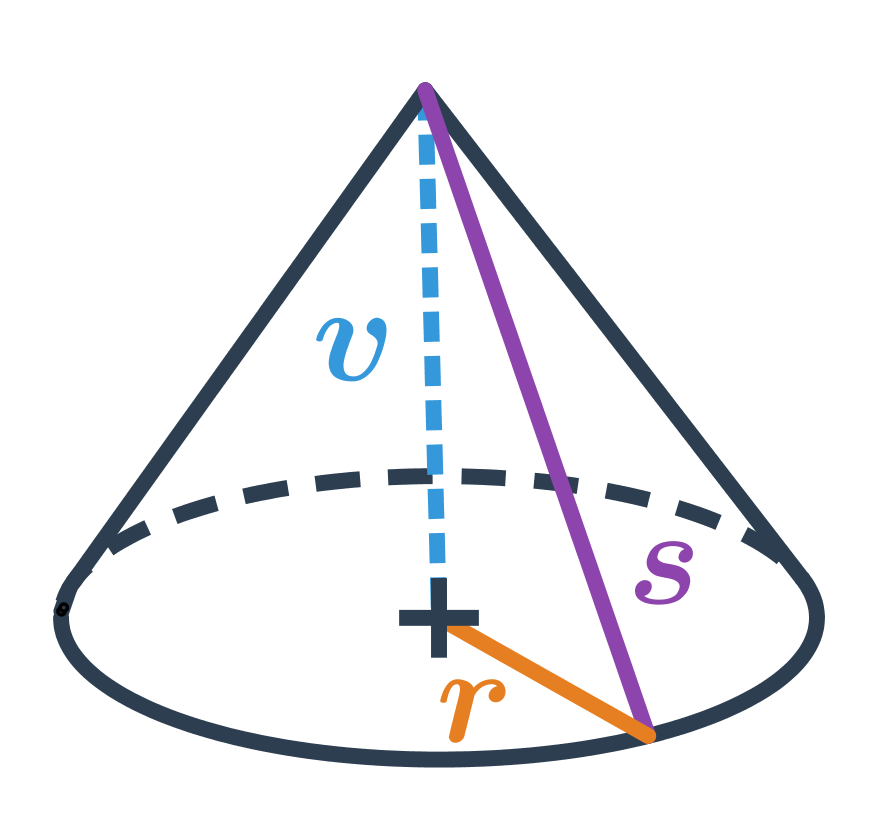
Môže sa stať, že poznáme polomer r podstavy kužeľa a jeho výšku v, ale nemáme zadanú jeho stranu s. Potom si stranu môžeme dopočítať ako preponu pravouhlého trojuholníka s odvesnami s dĺžkami v a r. Platí: s=\sqrt{v^2+r^2}
- Obsah podstavy kužeľa: \pi r^2
- Obsah plášťa kužeľa: \frac{1}{2} \cdot 2 \pi r \cdot s = \pi r s
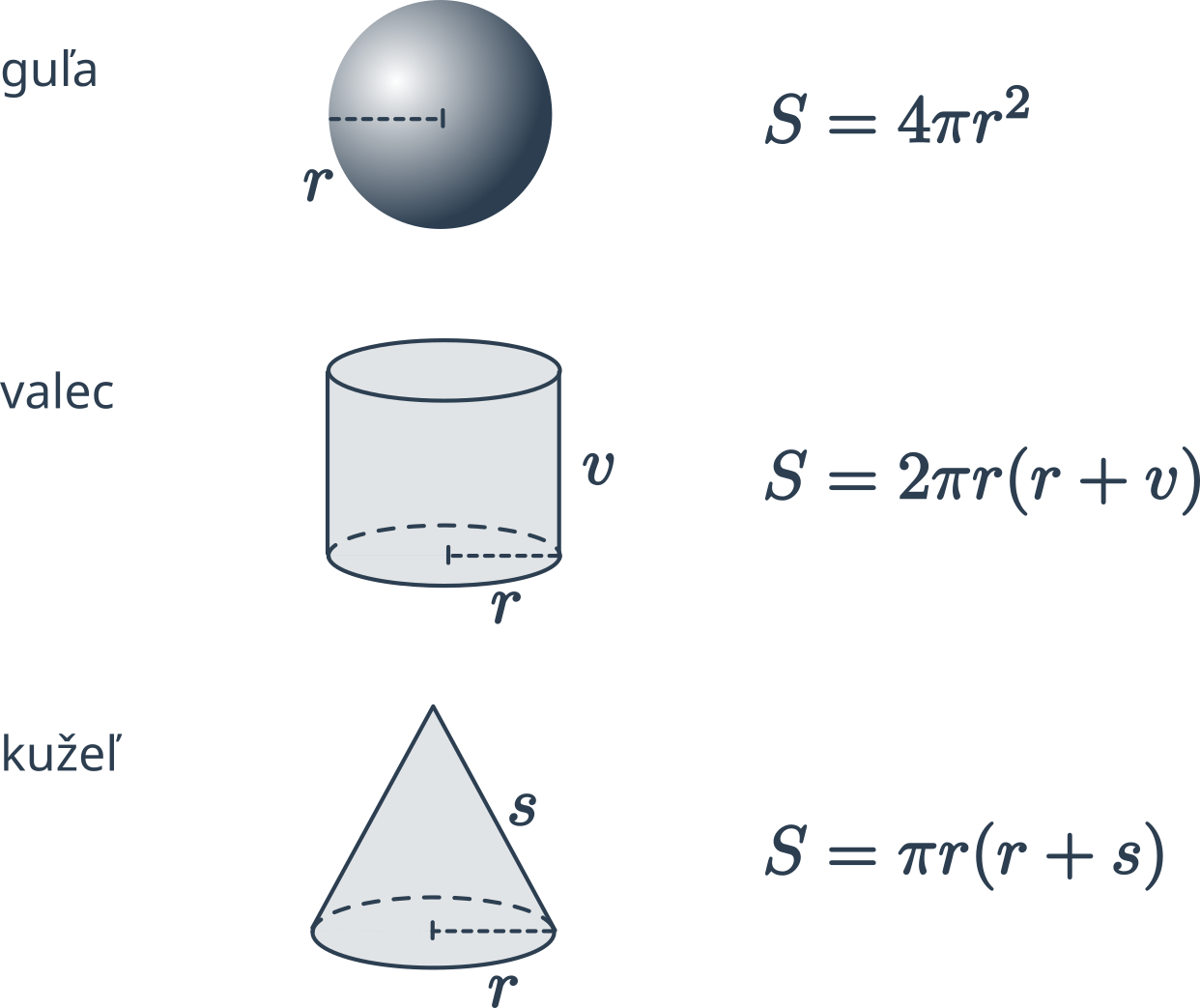
Povrch okrúhlych telies
Povrch „guľatých“ telies vypočítame s využitím konštanty \pi \approx 3{,}14 159 265. Vo vzorcoch označuje r polomer (gule či podstavy), v výšku valca, s stranu kužeľa.
- Povrch gule je S = 4\pi r^2.
- Povrch valca sa skladá z podstavy (dvakrát) a plášťa: S = 2\cdot \pi r^2 + 2\pi r v = 2\pi r (r+v).
- Povrch kužeľa sa skladá z podstavy a plášťa: S = \pi r^2 + \pi rs= \pi r(r+s).