Výpis prehľadov
Dĺžka a obvod
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Obvod trojuholníka
Obvod trojuholníka vypočítame ako súčet dĺžok jeho strán: o=a+b+c
Príklad:
Trojuholník na obrázku má dĺžky strán a=10, b=8, c=14, takže jeho obvod je o=a+b+c=10+8+14=32.
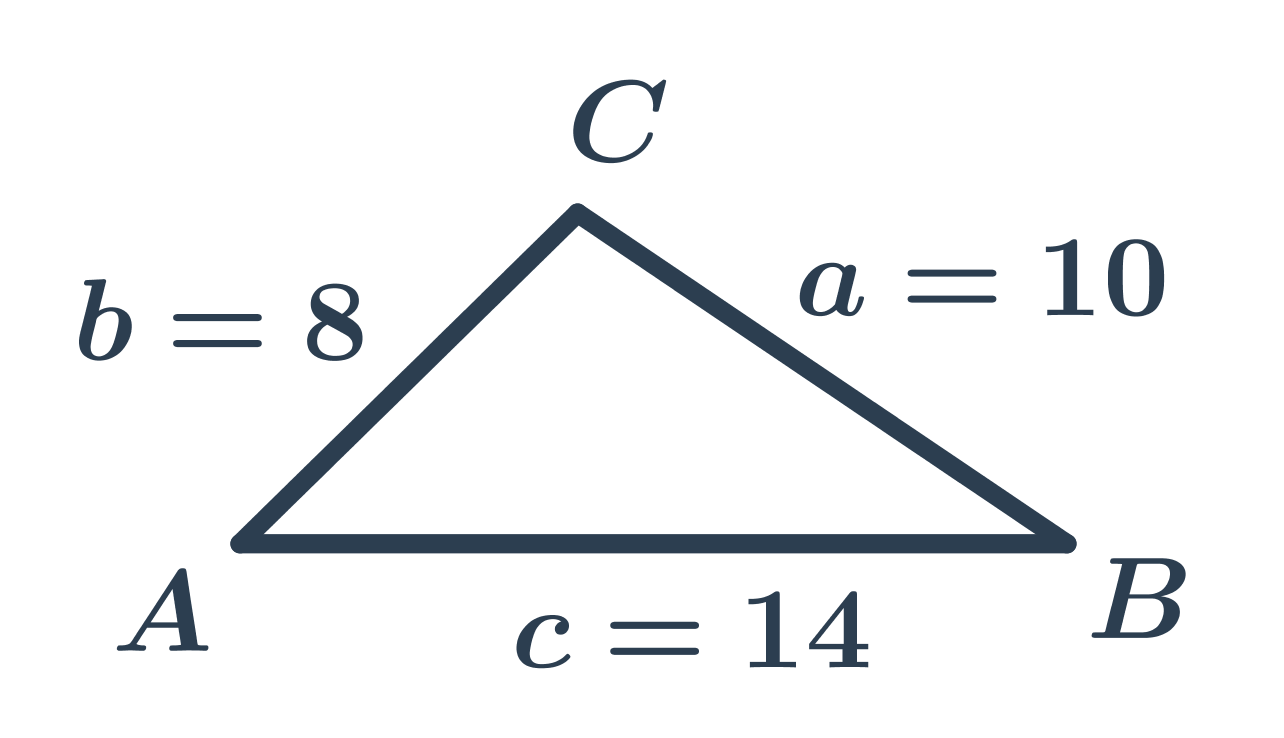
Obvod štvorca a obdĺžnika
Obvod štvorca so stranou s dĺžkou a je o=a+ a+a+a= 4a.
Obvod obdĺžnika so stranami s dĺžkami a,b je rovný o=a + b + a + b = 2\cdot (a+b).
HoreObvod rovnobežníka
Obvod rovnobežníka so stranami s dĺžkami a,b je rovný S=a + b + a + b = 2\cdot (a+b).
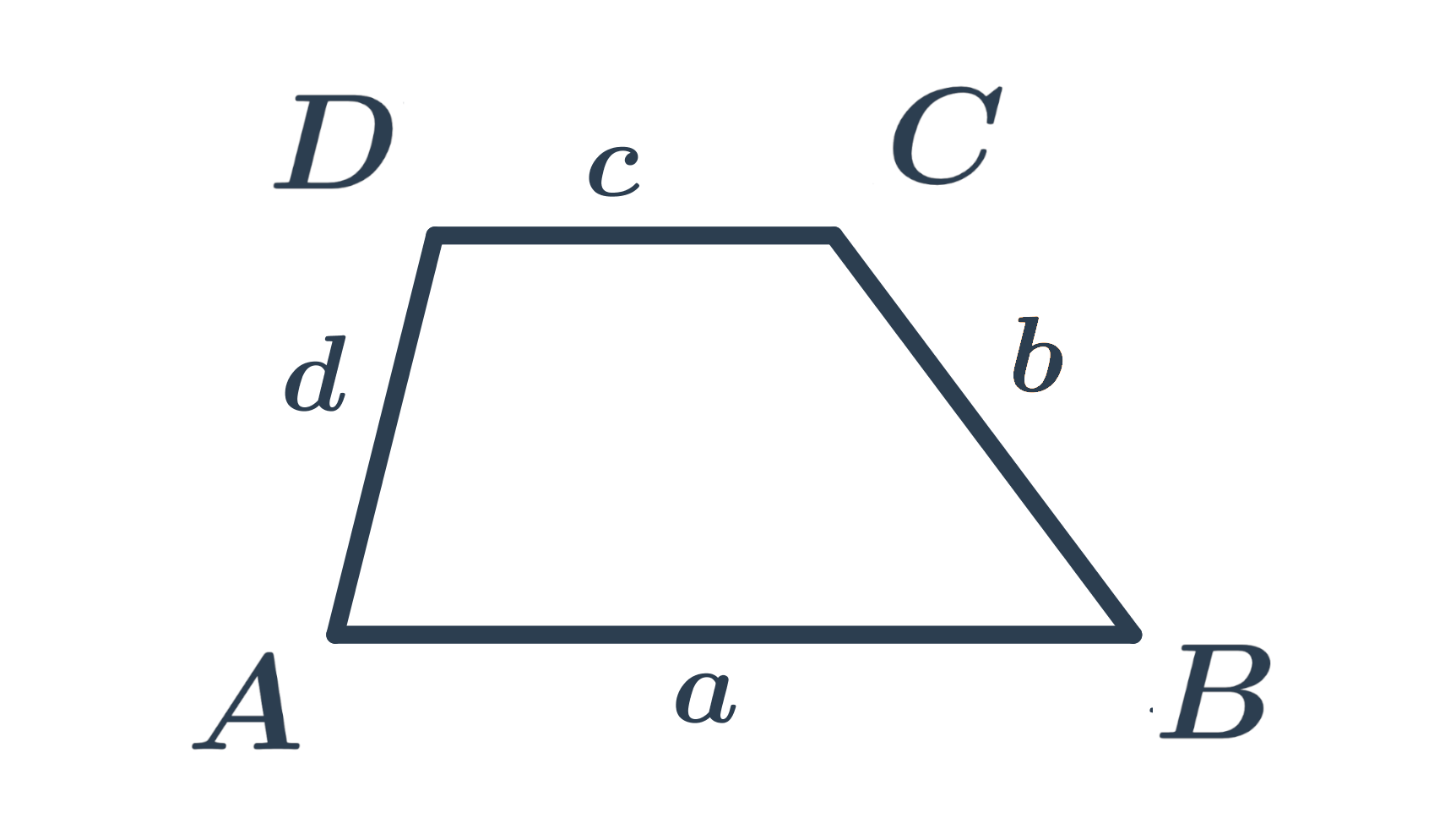
HoreObvod lichobežníka
Obvod lichobežníka je súčet dĺžok jeho strán. Teda obvod lichobežníka ABCD so stranami s dĺžkami a,b,c,d vypočítame podľa vzorčeka o=a+b+c+d.
Obvod kruhu, dĺžka kružnice
Vzorec pre obvod kruhu
Obvod kruhu (aj kružnice) s polomerom r je o=2\pi r. Pre priemer d platí o = \pi d.
Konštanta \pi sa tiež nazýva Ludolfovo číslo. \pi je iracionálne číslo, čo znamená, že nejde vyjadriť zlomkom ani zapísať presne v desiatkovej sústave. Približná hodnota \pi je 3,141 592 65.
Pri výpočte obvodu kruhu dávame dobrý pozor na to, či vychádzame zo znalosti polomeru alebo priemeru. Zámena priemeru za polomer je častou chybou.
Intuícia
Základnú intuíciu za vzorcom pre výpočet obvodu kruhu približuje nižšie uvedený obrázok. Obvod oranžového štvorca je 8\cdot r. Obvod kruhu je „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Príklady
- Majme kruh s polomerom 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm.
- Kružnica s priemerom 2 cm má dĺžku \pi \cdot 2 \approx 6,3 cm.
- Stredový kruh na futbalovom ihrisku má polomer 9{,}1 metra. Ak ho chceme obísť po jeho okrajovej čiare, prejdeme 2 \pi \cdot 9{,}1 \approx 57 metrov.
Dĺžka oblúka
Dĺžka oblúka
Dĺžku oblúka, ktorý na kružnici s polomerom r zodpovedá stredovému uhlu \alpha vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Príklady
- Dĺžka oblúka na obrázku je: \frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
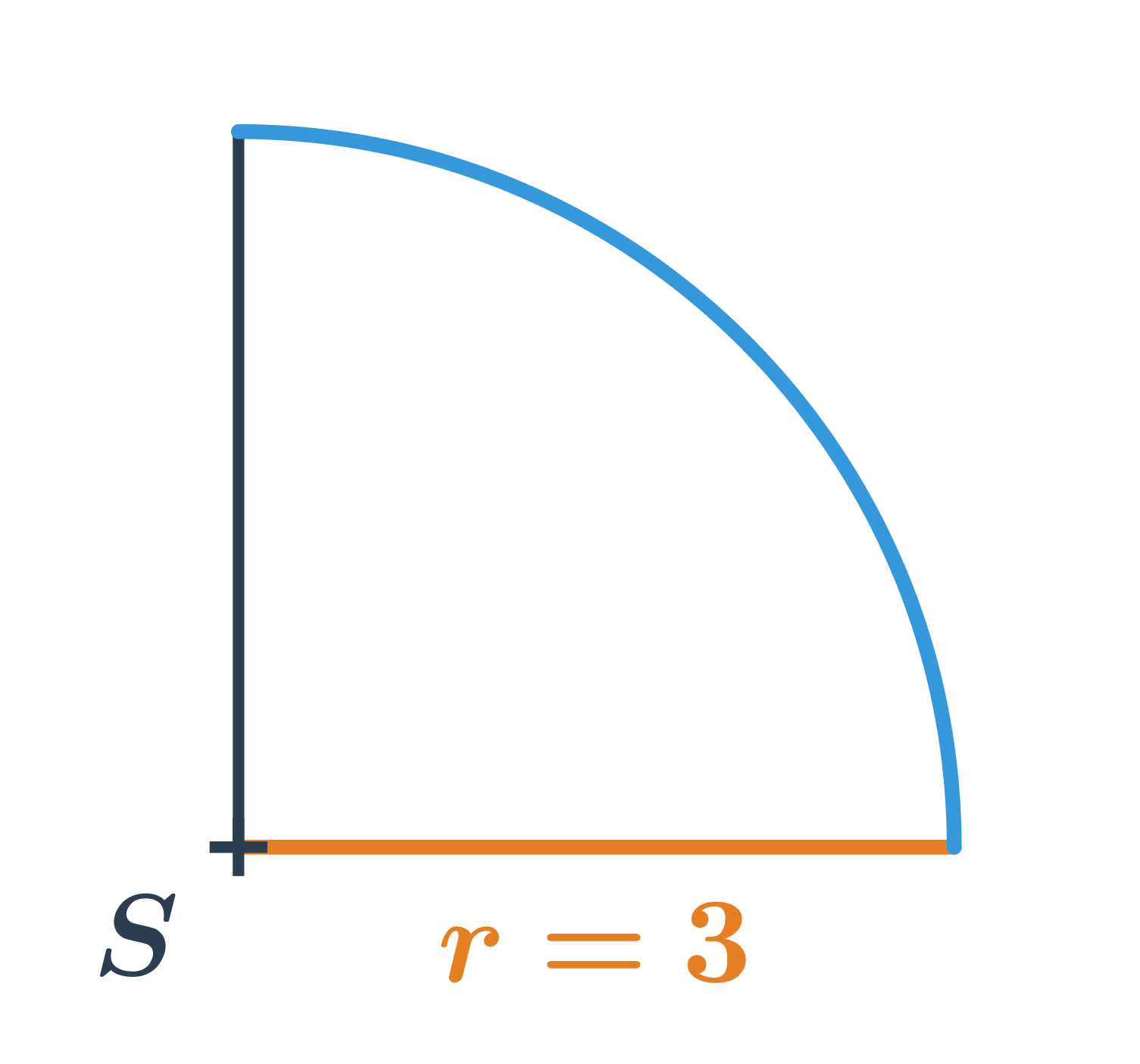
- Dĺžka celej kružnice (teda pre celých 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r
Obvod: mix
Obvod trojuholníkov a štvoruholníkov je jednoducho súčet dĺžok ich strán.
| Útvar | Vlastnosti | Obvod |
|---|---|---|
| trojuholník | strany a, b, c | o = a + b + c |
| štvorec | strana a | o = 4a |
| obdĺžnik | strany a, b | o = 2(a+b) |
| rovnobežník | strany a, b | o = 2(a+b) |
| všeobecný štvoruholník | strany a, b, c, d | o = a+b+c+d |

