Dlžník a veriteľ
Keď si niekto požičia peniaze, stáva sa dlžníkom. Požičanej čiastke sa hovorí istina. Ten, ktorý dlžníkovi peniaze požičal, sa označuje ako veriteľ (verí, že mu dlžník peniaze vráti). Za požičanie musí dlžník väčšinou veriteľovi zaplatiť ešte odmenu, tej sa hovorí úroky. Výšku úrokov stanovuje úroková miera (tiež úroková sadzba). Tá udáva, koľko percent z požičanej čiastky zaplatí dlžník navyše.
Príklady pôžičiek s úrokmi
| požičaná čiastka (istina) | úroková miera | úrok | čiastka na vrátenie |
| 10 000 € | 5 % | 500 € | 10 500 € |
| 46 000 € | 3 % | 1380 € | 46 350 € |
| 600 000 € | 7 % | 42 000 € | 642 000 € |
Vysoká a nízká úroková miera
Najčastejší vzťah dlžník vs. veriteľ vzniká medzi fyzickými osobami alebo firmami na jednej strane a bankami na strane druhej. Ak si od banky peniaze požičiame, je pre nás výhodná nízka úroková miera, aby sme nemuseli platiť veľa peňazí navyše. Keď naopak chceme vložiť peniaze na bankový šporiaci účet, poskytujeme tým banke pôžičku a stávame sa veriteľmi. Banka je tak dlžníkom a teda je pre nás výhodná vysoká úroková miera (aby sme dostali čo najviac peňazí navyše).
Úrokovacie obdobie
Pretože sa peniaze požičiavajú na rôzne dlhú dobu, je nutné úrokovú mieru vztiahnuť k časovému obdobiu. Je rozdiel, či zaplatíme za pôžičku naviac 5 % celkovo, 5 % ročne alebo 5 % za každý mesiac, kedy máme peniaze požičané. Úroková miera sa teda môže uvádzať
- za jeden rok (p. a.)
- za jeden mesiac (p. m.)
- za jeden polrok (p. s.)
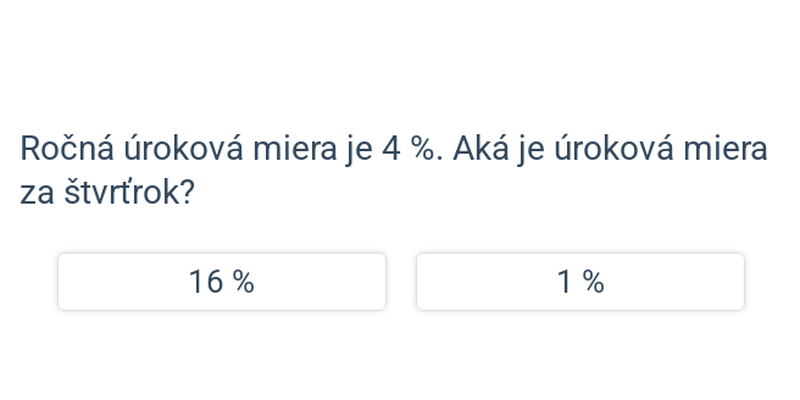
- za jeden štvrťrok (p. q.)
- za jeden deň (p. d.)
Ak nie je uvedené inak, vzťahuje sa úroková miera k jednému roku. Niekedy narazíte aj na mesačnú úrokovú mieru, ostatné sa používajú skôr výnimočne.
Pripisovanie úrokov
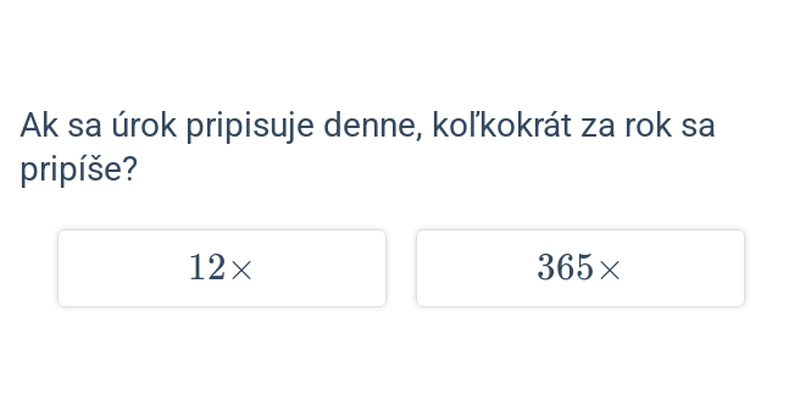
V praxi môžeme naraziť na to, že úroková miera je napr. 6 % ročne, ale úroky sa pridávajú mesačne. V takom prípade stačí ročnú úrokovú mieru vydeliť 12 (počet mesiacov v roku) a získame mesačnú úrokovú mieru. V uvedenom príklade by sa teda každý mesiac pripočítal úrok vo výške 0,5 % (6:12=0,5). V prípade jednoduchého úročenia je celková výška úroku na konci roku rovnaká (600 € = 12 krát 50 €).
Príklad – jednoduché úročenie, pripisovanie raz za rok
| investovaná čiastka (istina) | ročná úroková miera | úrok za rok |
| 10 000 € | 6 % | 600 € |
Príklad – jednoduché úročenie, pripisovanie raz za mesiac
| investovaná čiastka (istina) | mesačná úroková miera | úrok za mesiac | celkovo úroky za rok |
| 10 000 € | 0,5 % | 50 € | 50 krát 12 = 600 € |
Daň z úrokov
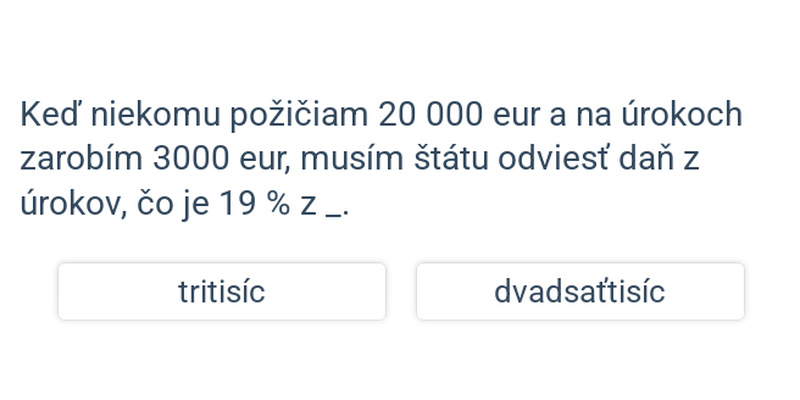
Vo väčšine prípadov sa zo získaných úrokov odvádza štátu daň vo výške 19 %. Ak teda peniaze požičiavame (napr. banke formou termínovaného vkladu alebo vkladaním peňazí na šporiaci účet), nedostaneme svoj úrok úplne celý – musíme z neho 19 % odčítať.
Príklady pôžičiek s úrokmi – počítanie s daňou
| investovaná čiastka (istina) | 10 000 € | 46 000 € | 600 000 € |
| úroková miera | 5 % | 3 % | 7 % |
| úrok | 500 € | 1380 € | 42 000 € |
| daň z úroku (%) | 19 % | 19 % | 19 % |
| daň z úroku (€) | 95 € | 262,2 € | 7 980 € |
| úrok po odčítaní dane | 405 € | 1117,8 € | 34 020 € |
| čiastka po pripísaní úroku | 10 405 € | 47 117,8 € | 634 020 € |
Jednoduché úročenie matematicky
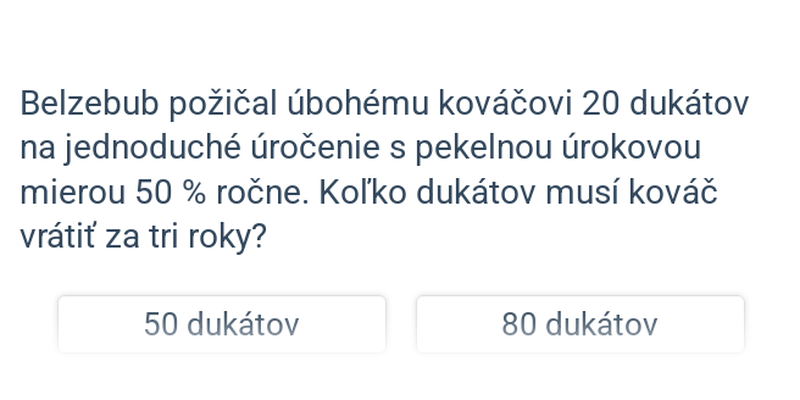
Pomocou matematiky môžeme vyjadriť, koľko celkovo peňazí naviac zaplatí dlžník na úrokoch. Vezmime si príklad, kedy veriteľ požičia dlžníkovi nejakú čiastku X a on ju chce vrátiť po n rokoch. Ročný úrok je p\ \%. Po n rokoch musí dlžník vrátiť X + n \cdot \frac{p}{100} \cdot X €.
Príklad – úroky po n rokoch
| investovaná čiastka (istina) | 30 000 € | X € |
| úroková miera | 10 % | p % |
| dlh vrátane úrokov 1. rok | 33 000 € | X + \frac{p}{100} \cdot X € |
| dlh vrátane úrokov 2. rok | 36 000 € | X + 2 \cdot \frac{p}{100} \cdot X € |
| dlh vrátane úrokov 3. rok | 39 000 € | X + 3 \cdot \frac{p}{100} \cdot X € |
| dlh vrátane úrokov 4. rok | 42 000 € | X + 4 \cdot \frac{p}{100} \cdot X € |
| dlh vrátane úrokov n. rok | 30 000 + n krát 3000 € | X + n \cdot \frac{p}{100} \cdot X € |
Všimnite si, že sa každý rok pripočítava rovnaká čiastka, ide teda o aritmetickú postupnosť.
Zhrnutie
Jednoduché úročenie je v zásade jednoduchý koncept platieb, ktoré platí dlžník veriteľovi za to, že mu požičal peniaze. Výška týchto poplatkov (úrokov) sa vypočíta pomocou percent (úroková miera) zo zapožičanej čiastky (istiny). Dôležité je dať pozor na to, ako často úroky pri jednej pôžičke vznikajú (úrokovacie obdobie a pripisovanie úrokov). Ak ste veriteľ, tak zo získaných úrokov väčšinou ešte musíte zaplatiť daň.
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Pexeso
Hľadanie dvojíc, ktoré k sebe patria.
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
Slovné úlohy
Klasické precvičovanie slovných úloh s pestrou ponukou zadaní a vysvetľujúcimi textami.