Rovnice

viemeto.eu/FWL

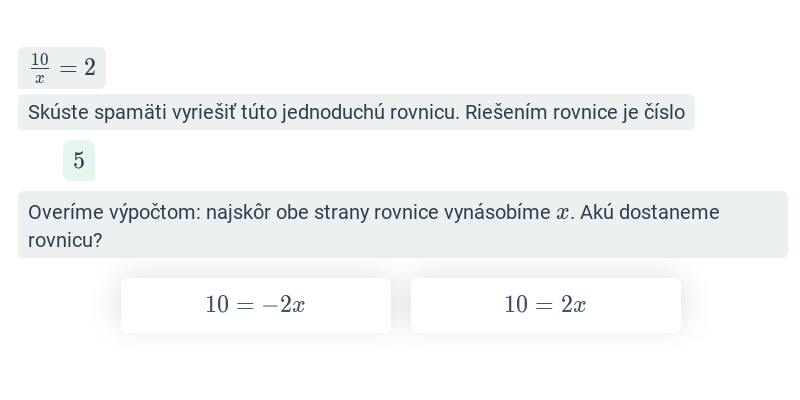
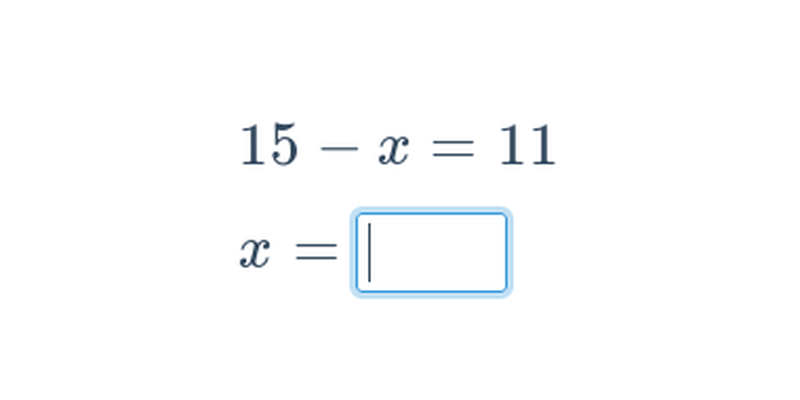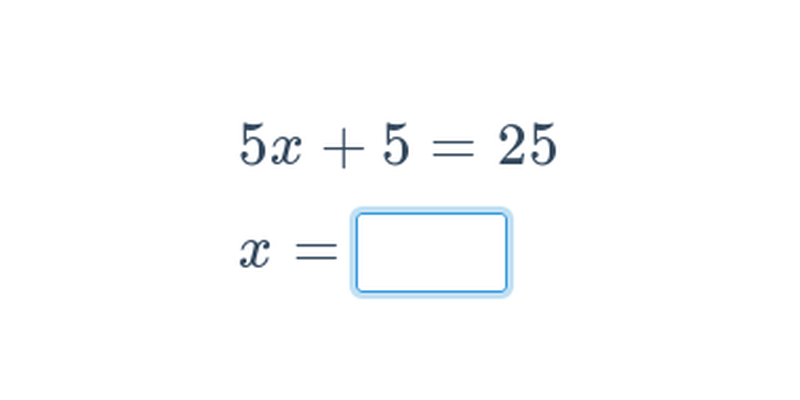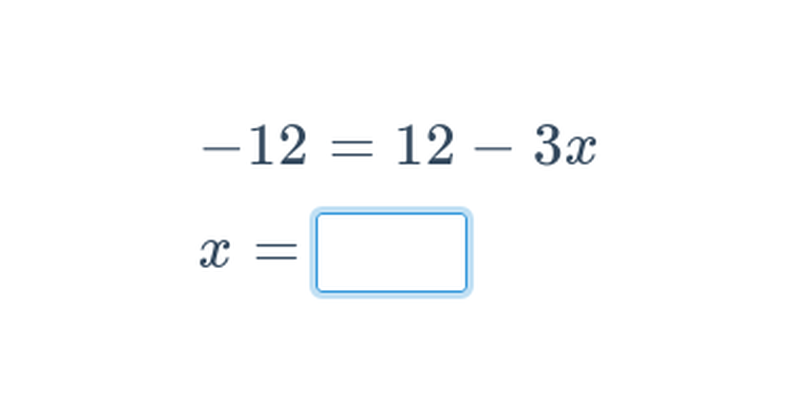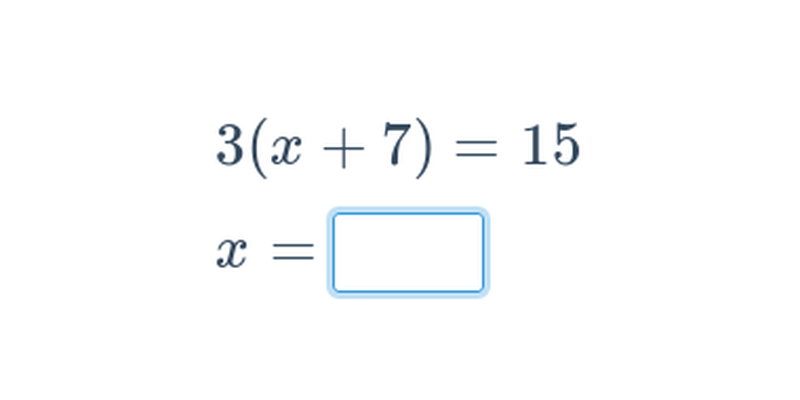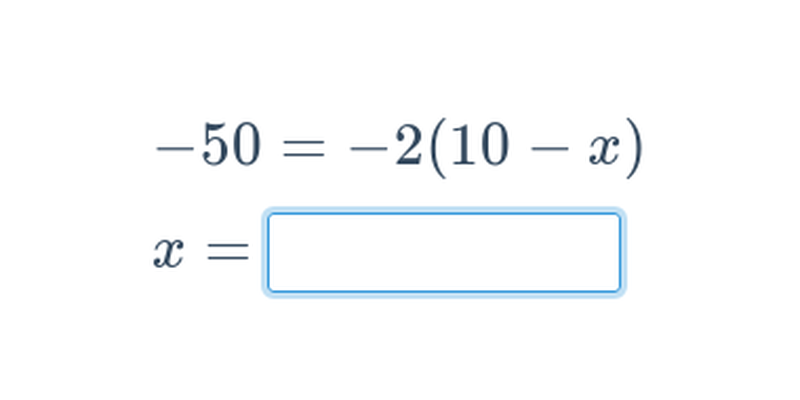Rovnica s neznámou x je zápis v tvare L(x) = P(x), kde L(x), P(x) sú výrazy s premennou x. L(x) je ľavá strana rovnice, P(x) je pravá strana rovnice. Riešiť rovnicu znamená nájsť všetky hodnoty premennej x, pre ktoré výrazy L(x) a P(x) nadobúdajú rovnaké hodnoty. Tieto čísla sa nazývajú korene rovnice. Výpočet hodnôt L(x) a P(x) pre konkrétne x sa nazýva skúška správnosti.

Príklad: riešme rovnicu 2x-7 = 5-4x.

ľavá strana	L(x) = 2x - 7
pravá strana	P(x) = 5-4x
koreň (riešenie) rovnice	x=2
skúška správnosti	L(x) = 2x-7 = 2\cdot 2 - 7= -3
	P(x) = 5-4x = 5 - 4\cdot 2 = -3

Rovnice delíme podľa typu výrazov, ktoré sa v nich objavujú. Napríklad:

lineárne rovnice obsahujú len konštanty a násobky premennej x, napríklad 7- 2x = -1,
kvadratické rovnice obsahujú aj druhú mocninu x, napríklad x^2+x-2=0,
logaritmické rovnice obsahujú \log(x), napríklad \log_2(1-x)=16,
exponenciálne rovnice obsahujú umocňovanie, v ktorom je premenná x v exponente, napríklad 3^x -3 = 6,
goniometrické rovnice obsahujú goniometrické funkcie, napríklad \sin(2x) = 1.

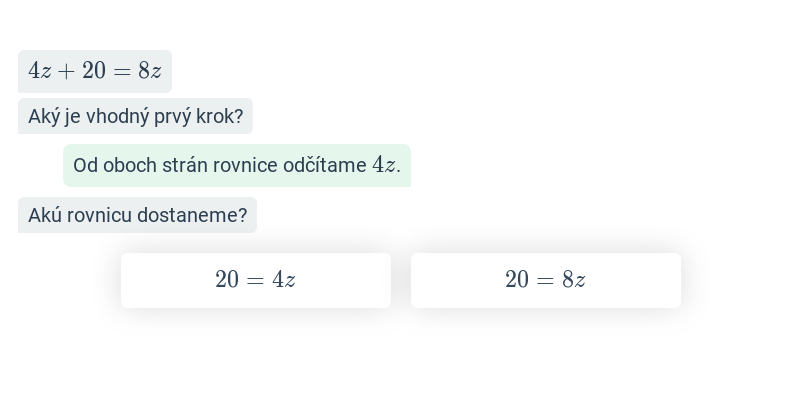
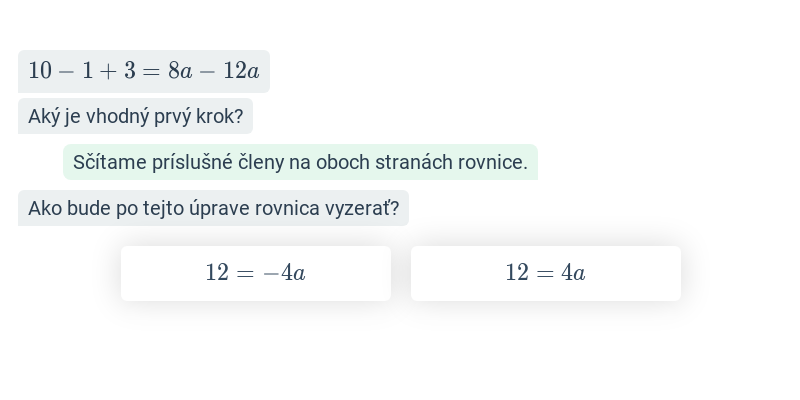
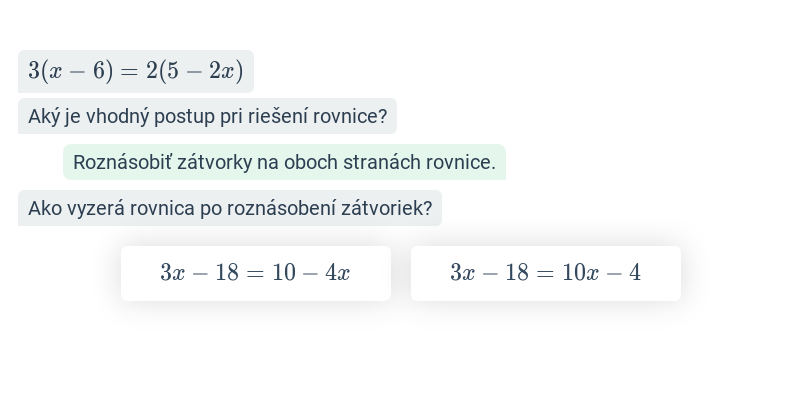
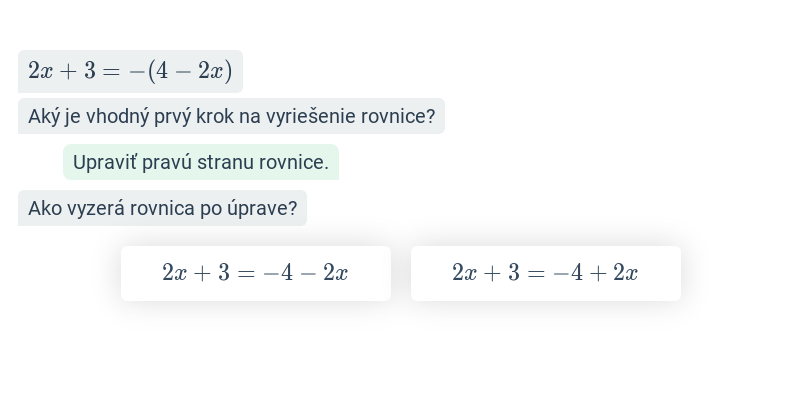
Rovnice riešime ekvivalentnými úpravami, čo sú úpravy, ktoré nemenia množinu koreňov rovnice. Medzi také úpravy patria napríklad:

výmena ľavej a pravej strany rovnice,
pripočítanie alebo odčítanie rovnakého výrazu k obom stranám/od obchod strán rovnice,
vynásobenie alebo vydelenie oboch strán rovnice nenulovým číslom.