Operácie s vektormi

Vektory v rovine môžu byť zapísané ako dvojice čísel – súradníc v rovine, podobne trojrozmerné vektory je možné zapísať ako trojice čísel – súradníc v priestore.

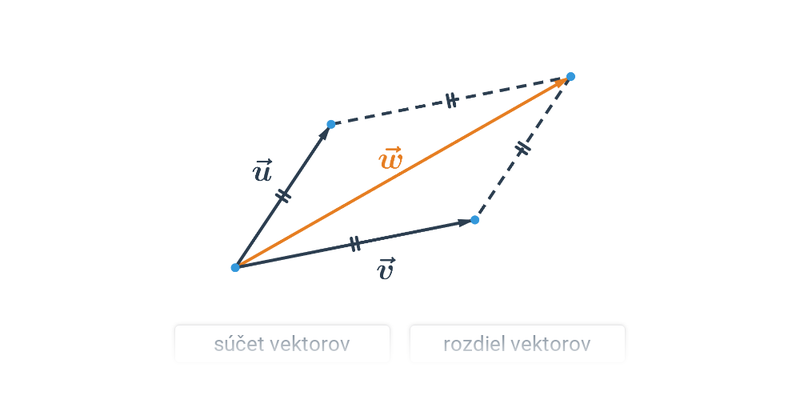
Operácie ako súčet, rozdiel a vynásobenie reálnym číslom, ktoré vieme jednoducho vykonávať s číslami, je možné s vektormi vykonávať po jednotlivých súradniciach. Tým sa zaoberá kapitolka Vektory: násobenie konštantou, súčet, rozdiel. Príklady praktického použitia týchto operácií s vektormi:

• vrabec letí rovnakým smerom ako mucha a dvakrát rýchlejšie než mucha – vektor rýchlosti vrabca získame, keď vektor rýchlosti muchy vynásobíme konštantou 2,
• satelitné snímky ukazujú, že ráno ešte vozidlo Marka Watneyho stálo na marsovskej základni, za dnes prekonal 50 km na východ – jeho novú polohu získame, keď k súradniciam základne pripočítame vektor (50;0),
• slimák preliezol rovno po monitore z ľavého horného rohu (súradnice v pixeloch [0;0]) do bodu [1007;555] – vektor, ktorého súradnice sú počty pixelov, ktoré slimák prekonal v horizontálnom a vertikálnom smere, získame ako rozdiel jeho umiestnenia na konci pohybu a jeho umiestnenia na začiatku pohybu.

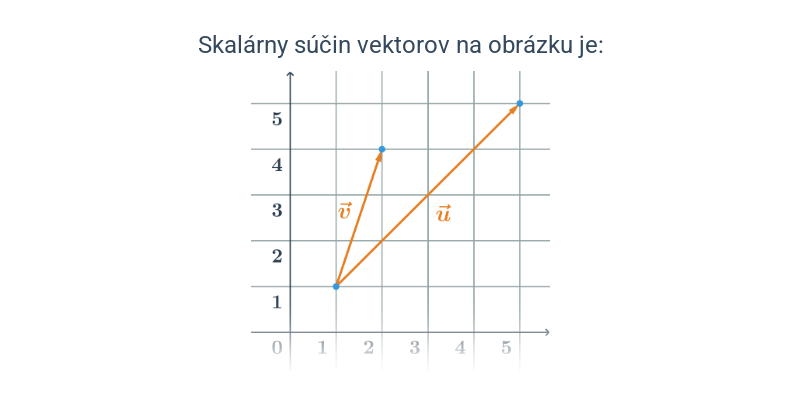
Špeciálna operácia, ktorú je možné vykonať s dvomi vektormi rovnakej dimenzie (majú rovnaký počet súradníc), je skalárny súčin. Vstup tejto operácie sú dva vektory, výstup je reálne číslo.

Vďaka skalárnemu súčinu môžeme vypočítať napríklad aký uhol vektory zvierajú, špeciálne či sú na seba kolmé (v takom prípade ich skalárny súčin vyjde nulový).