Pre exponenciálnu funkciu f:y =a^x platí:
- definičný obor D(f)=\R
- obor hodnôt H(f)=(0, \infty)
- je prostá
- nie je periodická
- nie je párna ani nepárna
- nemá maximum ani minimum
- je zdola ohraničená
Ďalšie vlastnosti závisia od hodnoty koeficientu a:
- pre a>1 je exponenciálna funkcia rastúca
- pre a\in (0,1) je exponenciálna funkcia klesajúca
Príklad: vlastnosti funkcie f\!: y =3^x
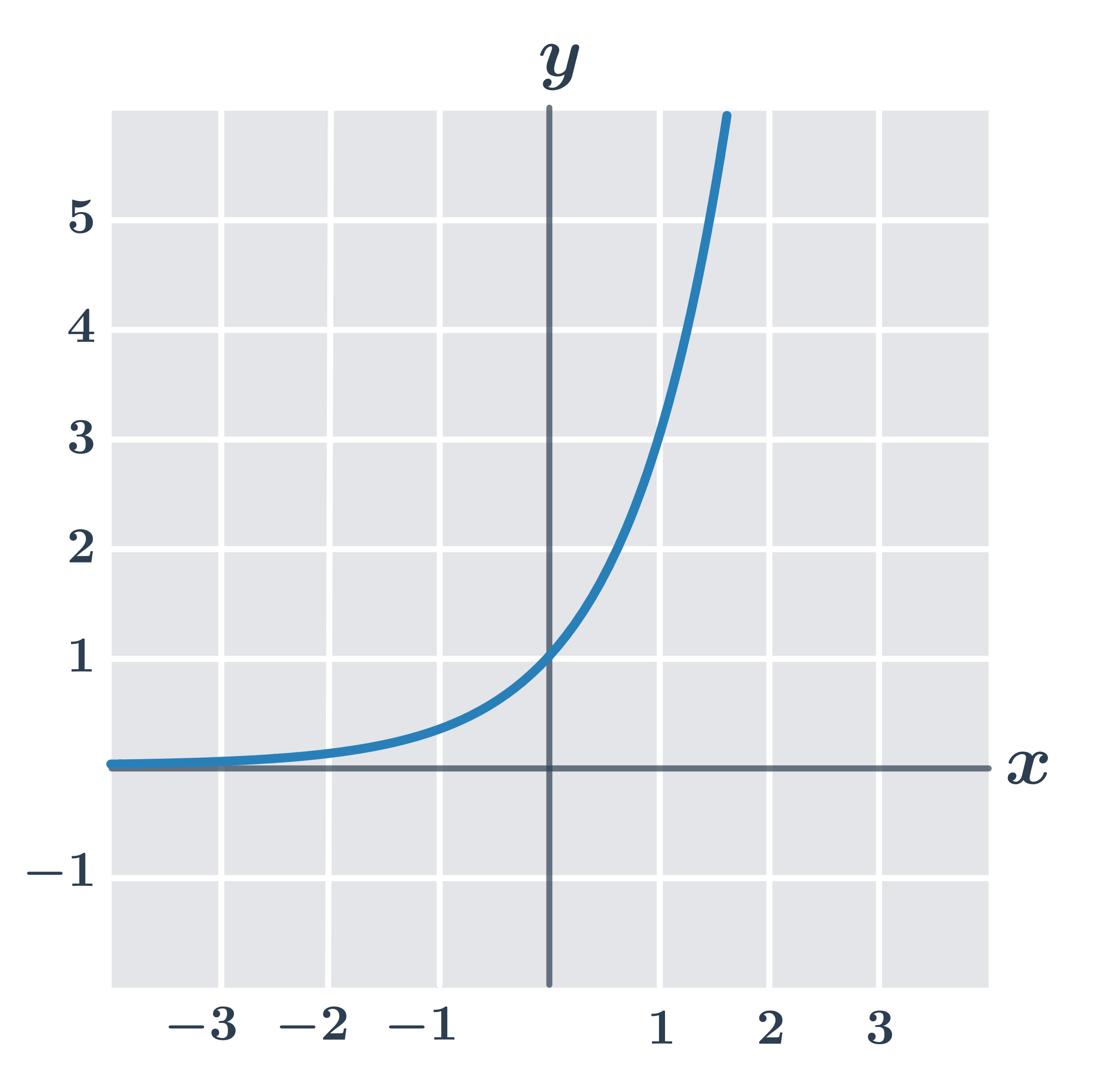
- definičný obor D(f)=\R
- obor hodnôt H(f)=(0, \infty)
- je prostá
- je zdola ohraničená
- je rastúca
Príklad: vlastnosti funkcie f\!: y=\left (\frac{1}{2}\right)^x
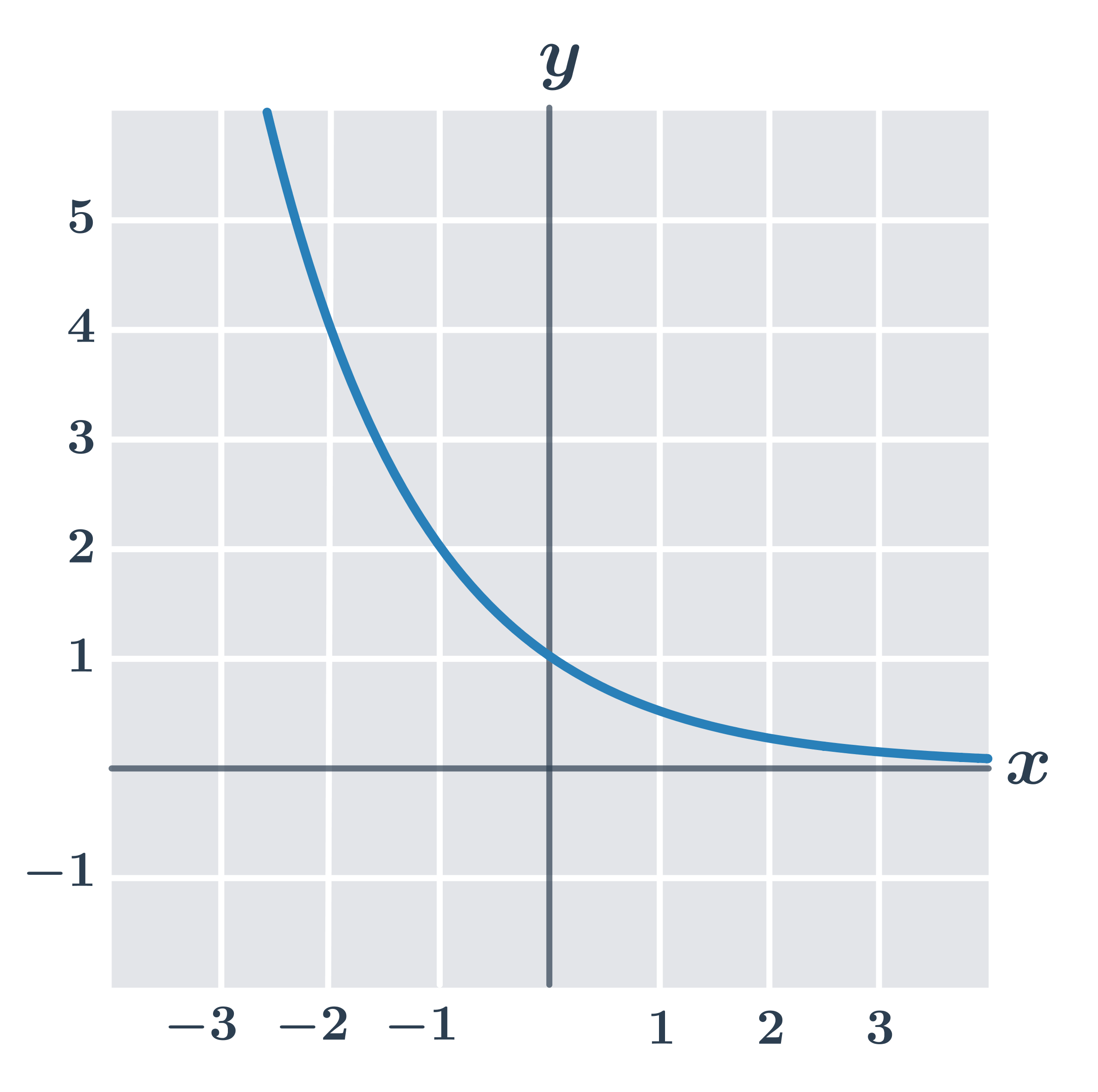
- definičný obor D(f)=\R
- obor hodnôt H(f)=(0, \infty)
- je prostá
- je zdola ohraničená
- je klesajúca
Pre túto tému (a prípadne zvolený ročník) zatiaľ nie je dostupné žiadne precvičovanie.
