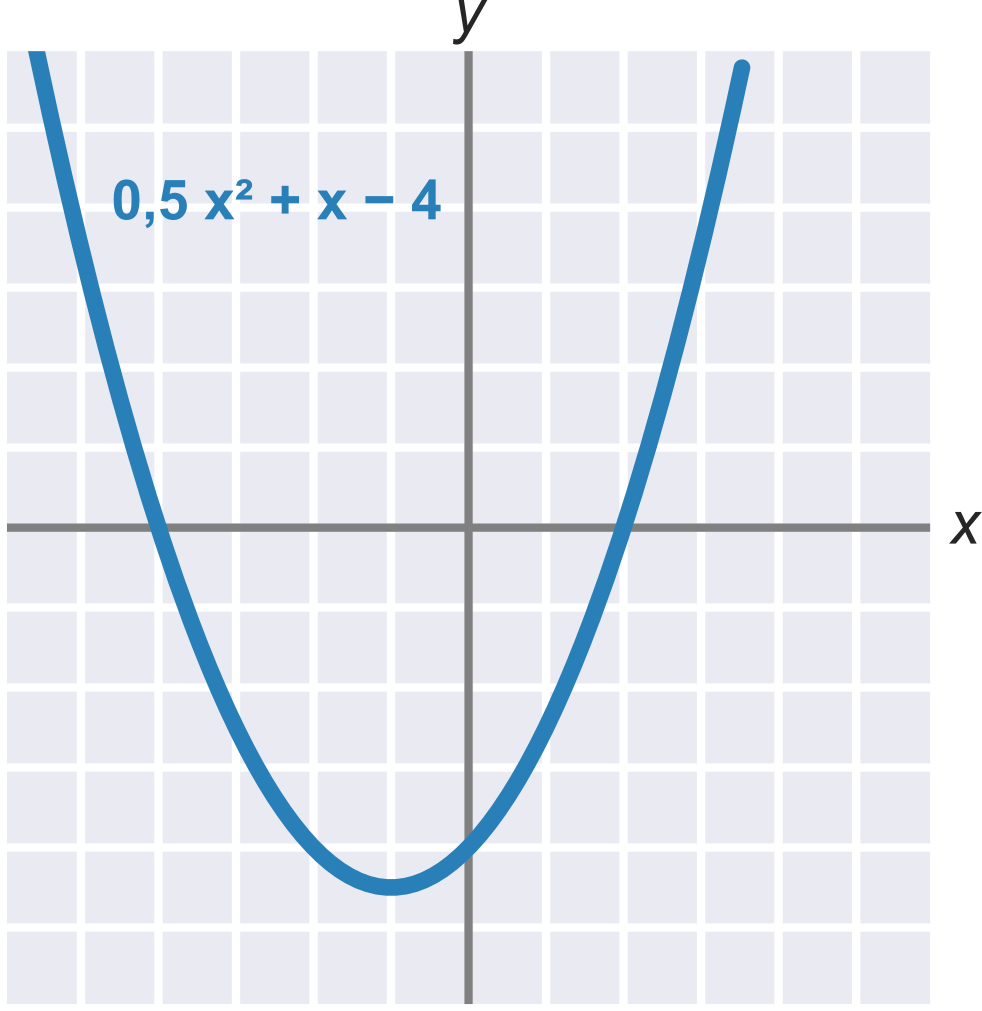
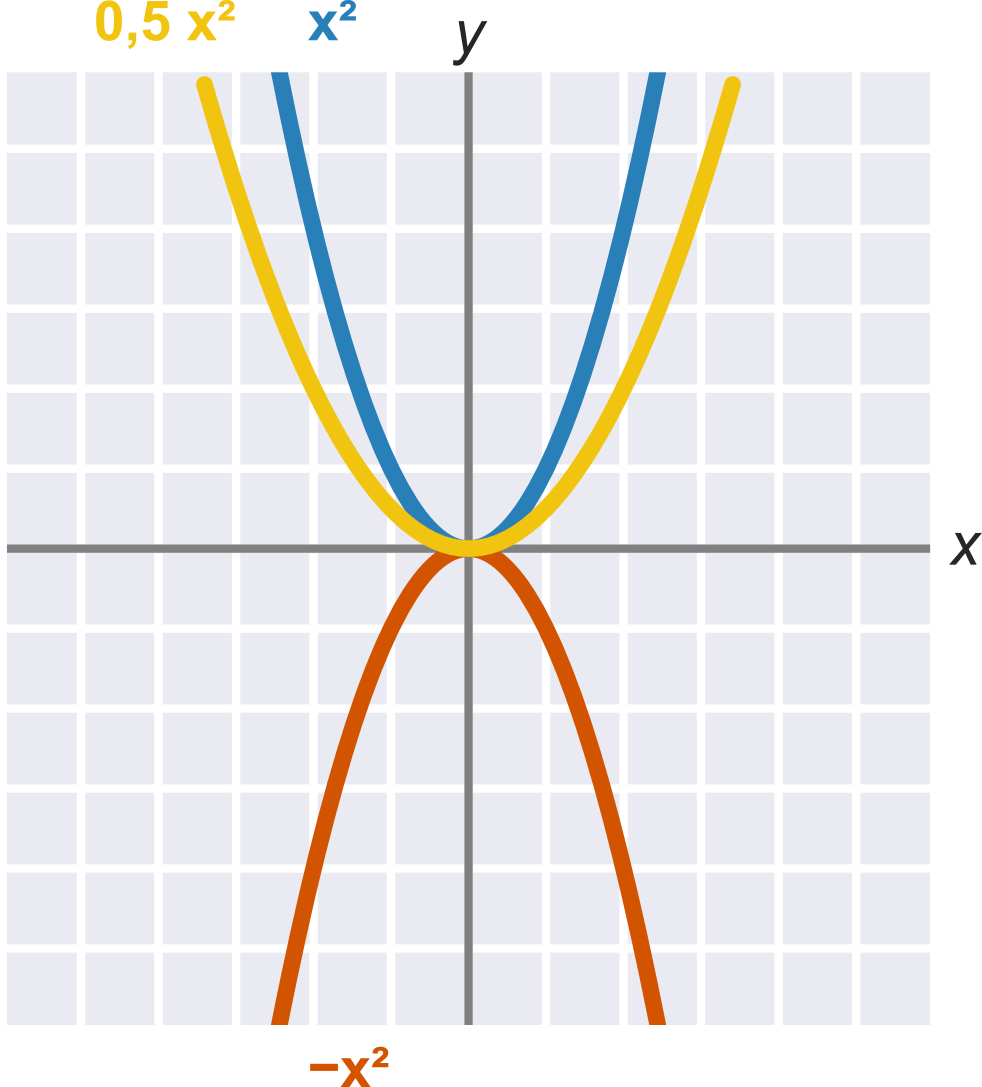
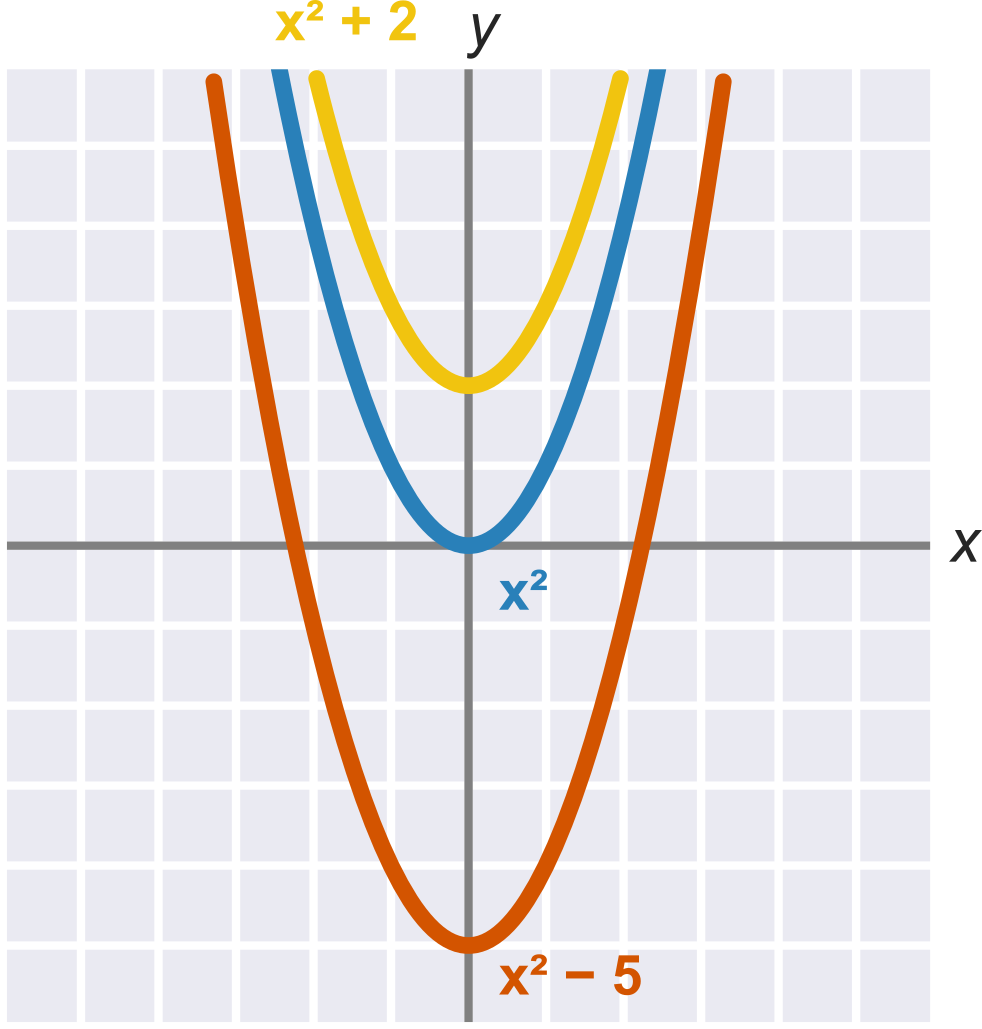
Výborne, je dosiahnutý %% štít
Grafy kvadratických funkcií » Grafár »
Prejsť na tému:
Grafy kvadratických funkcií
Grafy kvadratických funkcií
Prejsť na cvičenie:
Grafár
Grafár
Zobraziť na celú obrazovku
Zobraziť súhrn témy
Zdieľať
QR kód
QR kód je možné naskenovať napr. mobilným telefónom a tak sa dostať priamo k danému cvičeniu alebo sade príkladov.
Kód / krátka adresa
Trojznakový kód je možné napísať do vyhľadávacieho riadka, tiež je súčasťou skrátenej adresy.
Skopírujte kliknutím.
E6C
viemeto.eu/E6C
Grafy kvadratických funkcií (ťažké)