
Vzdialenosť bodu od priamky

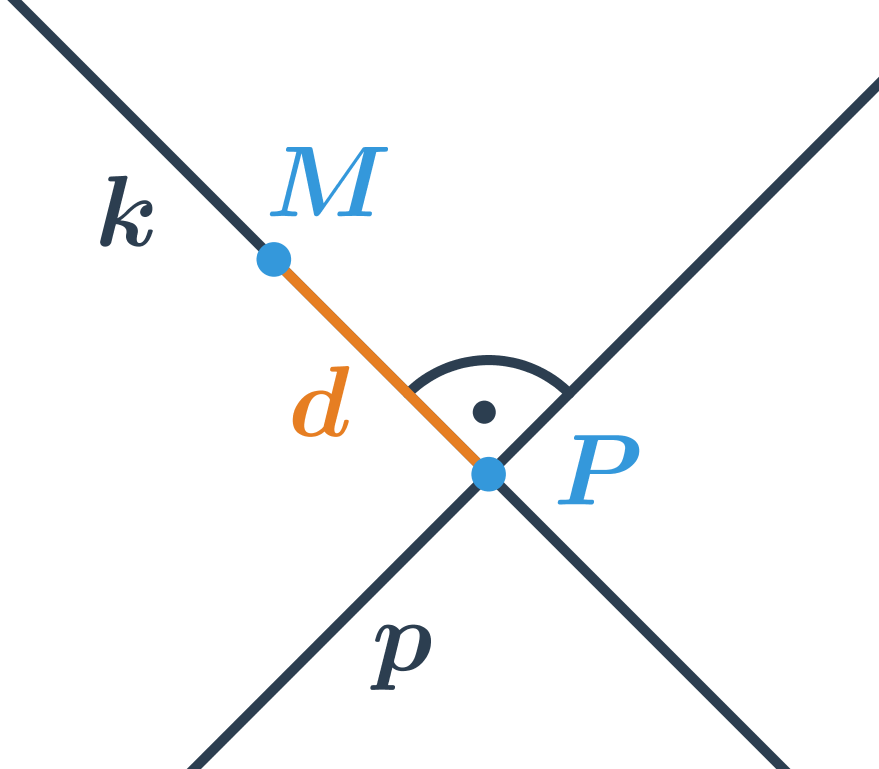
Vzdialenosť bodu od priamky je dĺžka najkratšej úsečky určenej bodom M a bodom ležiacim na priamke p. Ako je vidieť z obrázka, táto najkratšia úsečka leží na kolmici z bodu M k priamke p. Vzdialenosť bodu od priamky teda môžeme určiť takto:
- nájdeme priamku k, ktorá prechádza bodom M a je kolmá na priamku p
- určíme priesečník P priamky k s priamkou p
- vzdialenosť bodu M od priamky p je dĺžka úsečky PM
Príklad: vzdialenosť bodu od priamky – pomocou kolmice
Určite vzdialenosť bodu M=[5;2] od priamky p:4x+3y-1=0.
- Priamka k, ktorá prechádza bodom M a je kolmá na priamku p má smerový vektor kolineárny s normálovým vektorom priamky p.
- Súradnice smerového vektora priamky k sú: \vec{u}=(4;3).
- Priamka k má parametrické vyjadrenie: p:X=M+t\vec{u}
- p:\begin{array}{rrl}x&=&5+4t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
- Súradnice priesečníka P priamky k s priamkou p určíme dosadením parametrického vyjadrenia priamky k do všeobecnej rovnice priamky p.
\begin{array}{rrl}4(5+4t)+3(2+3t)-1&=&0\\20+16t+6+9t-1&=&0\\25+25t&=&0\Rightarrow t=-1\end{array}
- Priesečník priamok k a p je bod P=[1;-1].
- Vzdialenosť bodu M od priamky p je dĺžka úsečky PM:
- Vzorec pre dĺžku úsečky: d=\sqrt{(x_M-x_P)^2+(y_M-y_P)^2}
- Dosadíme súradnice bodov M,P: d=\sqrt{(5-1)^2+(2-(-1))^2}=\sqrt{16+9}=5
Vzorec pre vzdialenosť bodu od priamky danej všeobecnou rovnicou
Vzdialenosť bodu M=[m_1;m_2] od priamky p danej všeobecnou rovnicou ax+by+c=0 je daná vzorcom: d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}}
Príklad: vzdialenosť bodu od priamky – pomocou vzorca
Určite vzdialenosť bodu M=[5;2] od priamky p:4x+3y-1=0 s využitím vzorca.
- Dosadíme do vzorca d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} súradnice bodu M=[5;2] a koeficienty a a b zo všeobecnej rovnice priamky.
- Všeobecná rovnica pre p je 4x+3y-1=0, teda a=4 a b=3.
- Máme: d=\frac{\left| 4\cdot5+3\cdot2-1\right|}{\sqrt{4^2+3^2}}=\frac{25}{\sqrt{25}}=5
Vzdialenosť dvoch rovnobežiek
Ak vieme určiť vzdialenosť bodu od priamky, ľahko určíme tiež vzdialenosť dvoch rovnobežiek. Stačí si uvedomiť, že všetky body ležiace na jednej priamke majú od druhej priamky rovnakú vzdialenosť. Preto je vzdialenosť rovnobežiek rovnaká ako vzdialenosť ľubovoľného bodu na jednej priamke od priamky druhej.
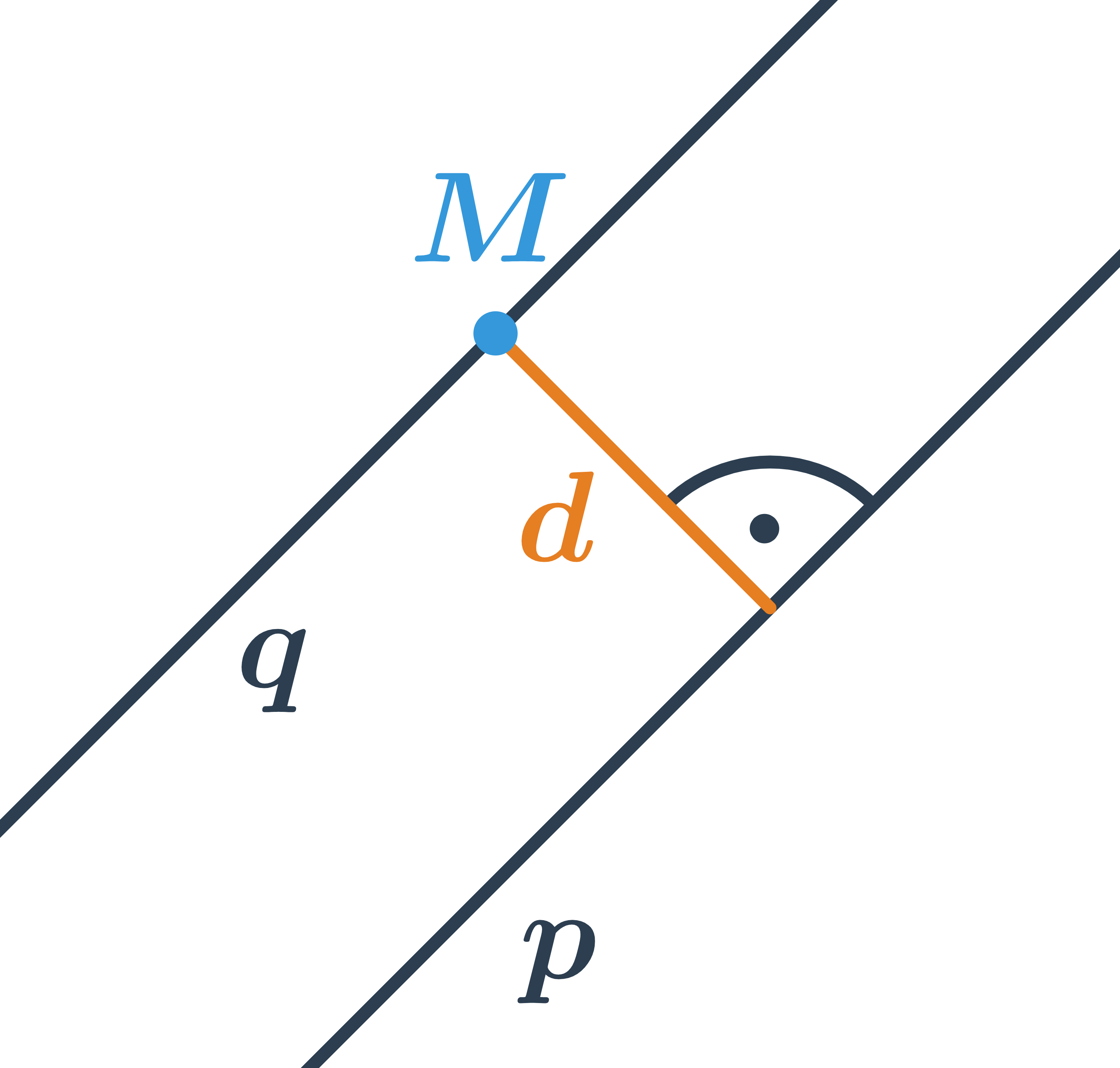
Príklad: vzdialenosť rovnobežiek
Určite vzdialenosť rovnobežiek p:2x-4y+3=0 a q:x-2y+1=0.
- Určíme súradnice jedného bodu (M) na priamke q tak, že jednu súradnicu zvolíme a druhú dopočítame.
- Zvolíme napríklad súradnicu y=0, potom x-2\cdot0+1=0\Rightarrow x=-1
- Dosadíme do vzorca d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} súradnice bodu M=[-1;0] a koeficienty a a b zo všeobecnej rovnice priamky p.
- Všeobecná rovnica pre p je 2x-4y+3=0, teda a=2 a b=-4.
- Máme: d=\frac{\left| 2\cdot(-1)-4\cdot0+3\right|}{\sqrt{2^2+(-4)^2}}=\frac{1}{\sqrt{20}}
- Vzdialenosť rovnobežiek p a q je: d=\frac{1}{\sqrt{20}}
Zatvoriť











