Obsah kruhového výseku

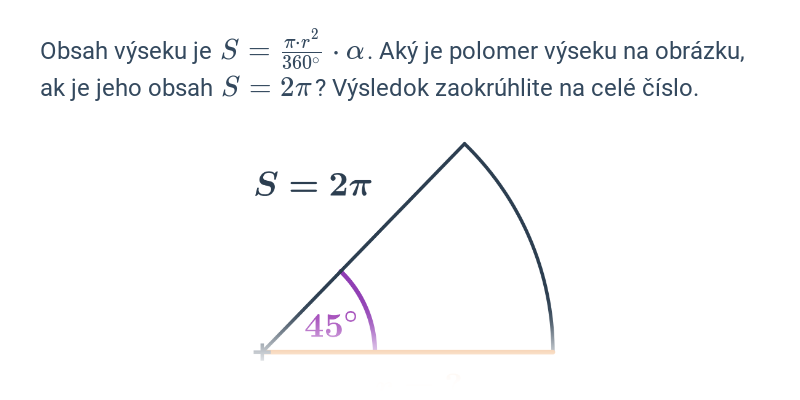
Obsah kruhového výseku

Obsah kruhového výseku so stredovým uhlom \alpha a polomerom r vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2

Dĺžka oblúka

Podobne, dĺžku oblúka, ktorý na kružnici s polomerom r a zodpovedá stredovému uhlu \alpha vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r

Príklady

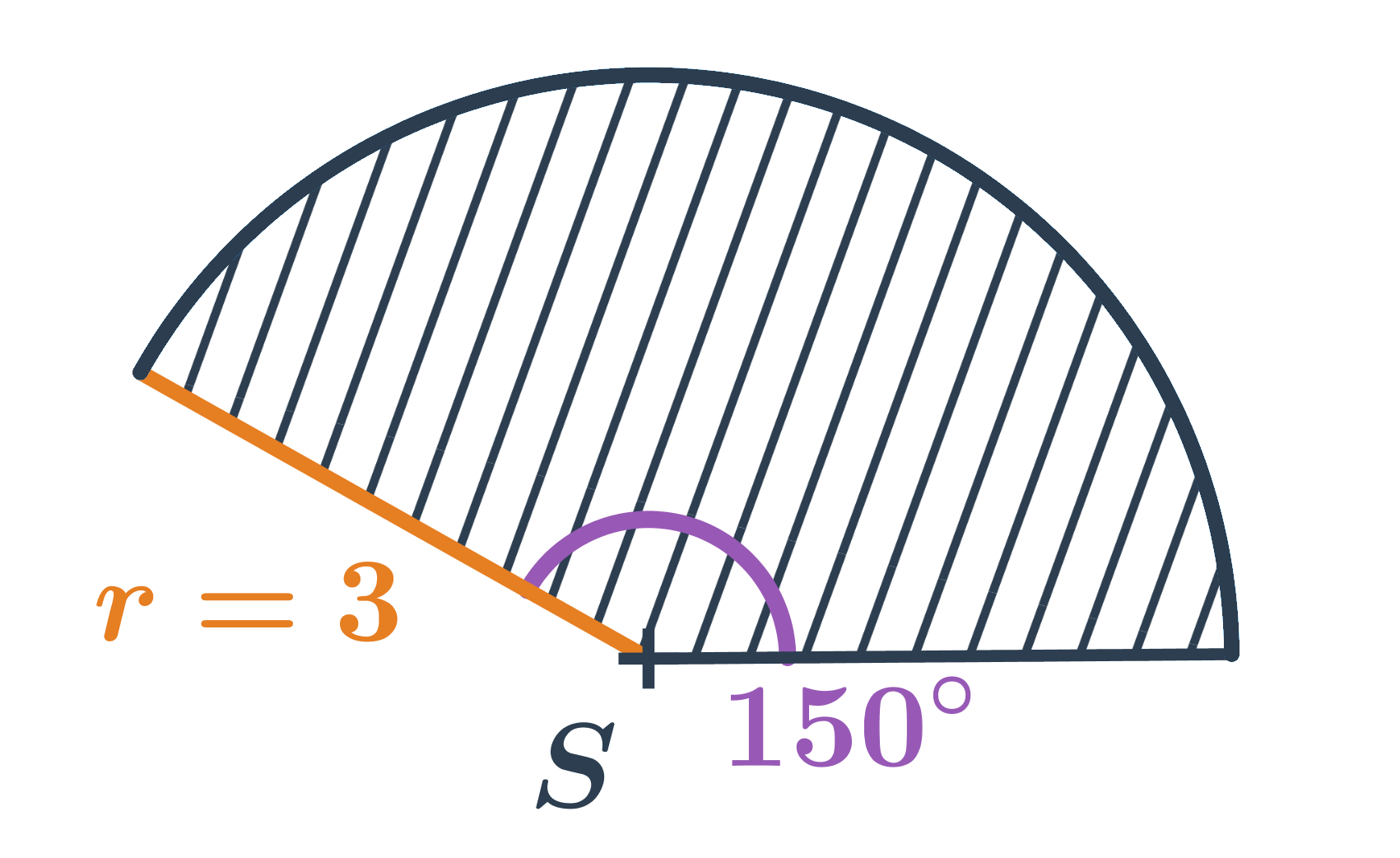
• Kruhový výsek na obrázku má obsah: \frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi

• Obsah celého kruhu (výseku so stredovým uhlom 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2
• Dĺžka oblúka na obrázku je: \frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi

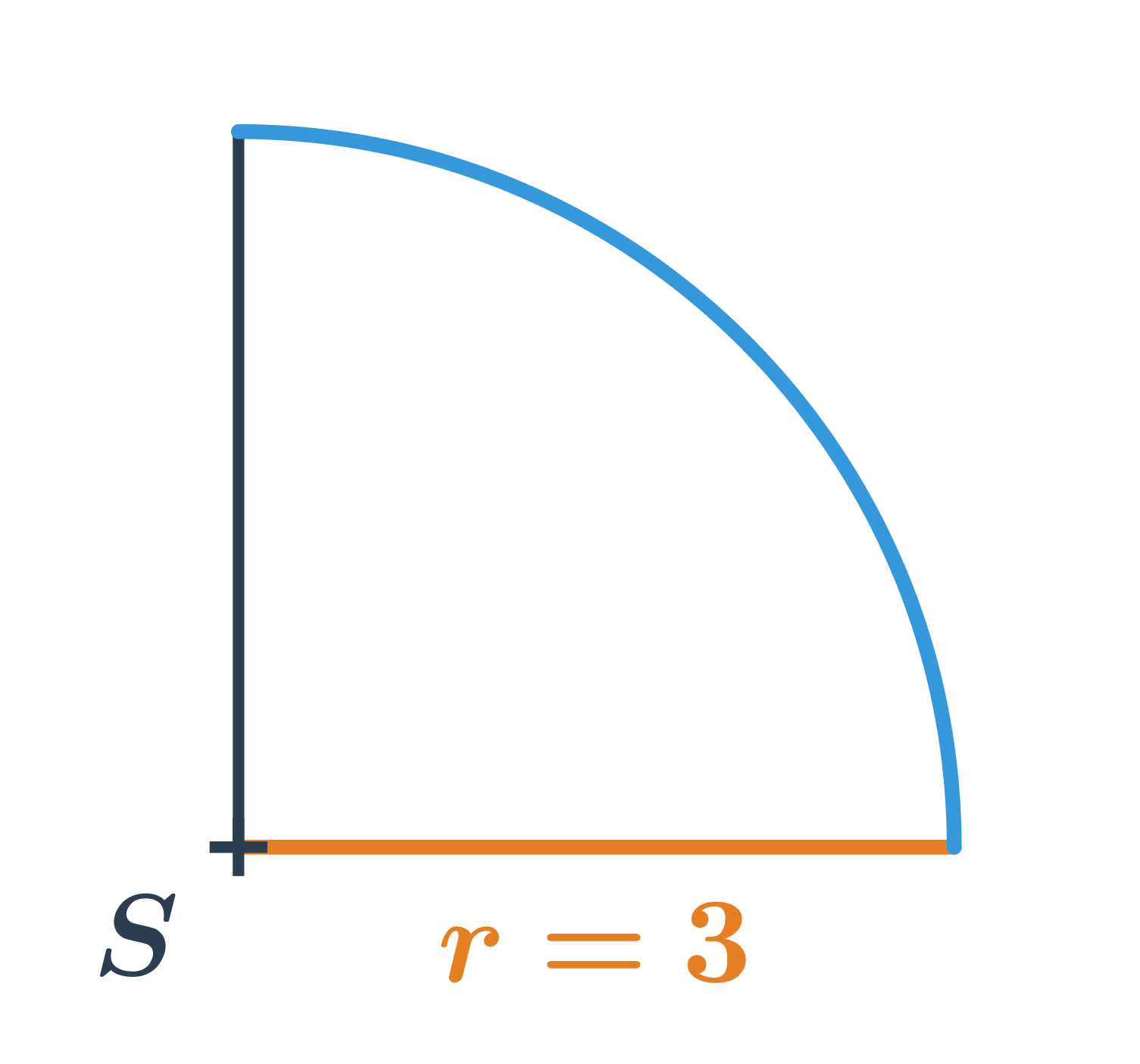
• Dĺžka celej kružnice (teda pre celých 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r