Parabola

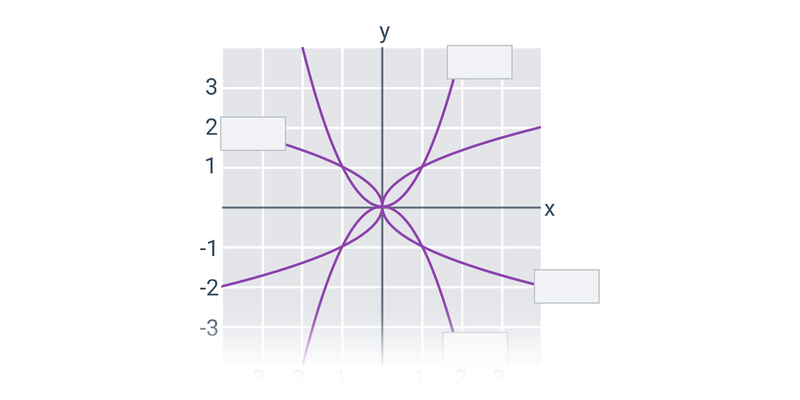
Parabola je množina všetkých bodov roviny, ktoré majú rovnakú vzdialenosť od daného bodu (ohnisko) a danej priamky (riadiaca priamka).

Vrcholová rovnica paraboly

Tvar rovnice závisí od umiestnenia osi:

• os paraboly rovnobežná s osou $y$, vrcholová rovnice má potom tvar: $(x-m)^2=\pm 2p(y-n)$
• os paraboly rovnobežná s osou $x$, vrcholová rovnica má potom tvar: $(y-n)^2=\pm 2p(x-m)$

V rovnici paraboly označujú $m$, $n$ súradnice vrcholu paraboly, teda vrchol je bod $V=[m;n]$. Ďalej $p$ je parameter paraboly = vzdialenosť ohniska od riadiacej priamky. Znamienko pred parametrom závisí od polohy na vrchole vzhľadom k bodom paraboly.

Príklad paraboly s osou rovnobežnou s osou y

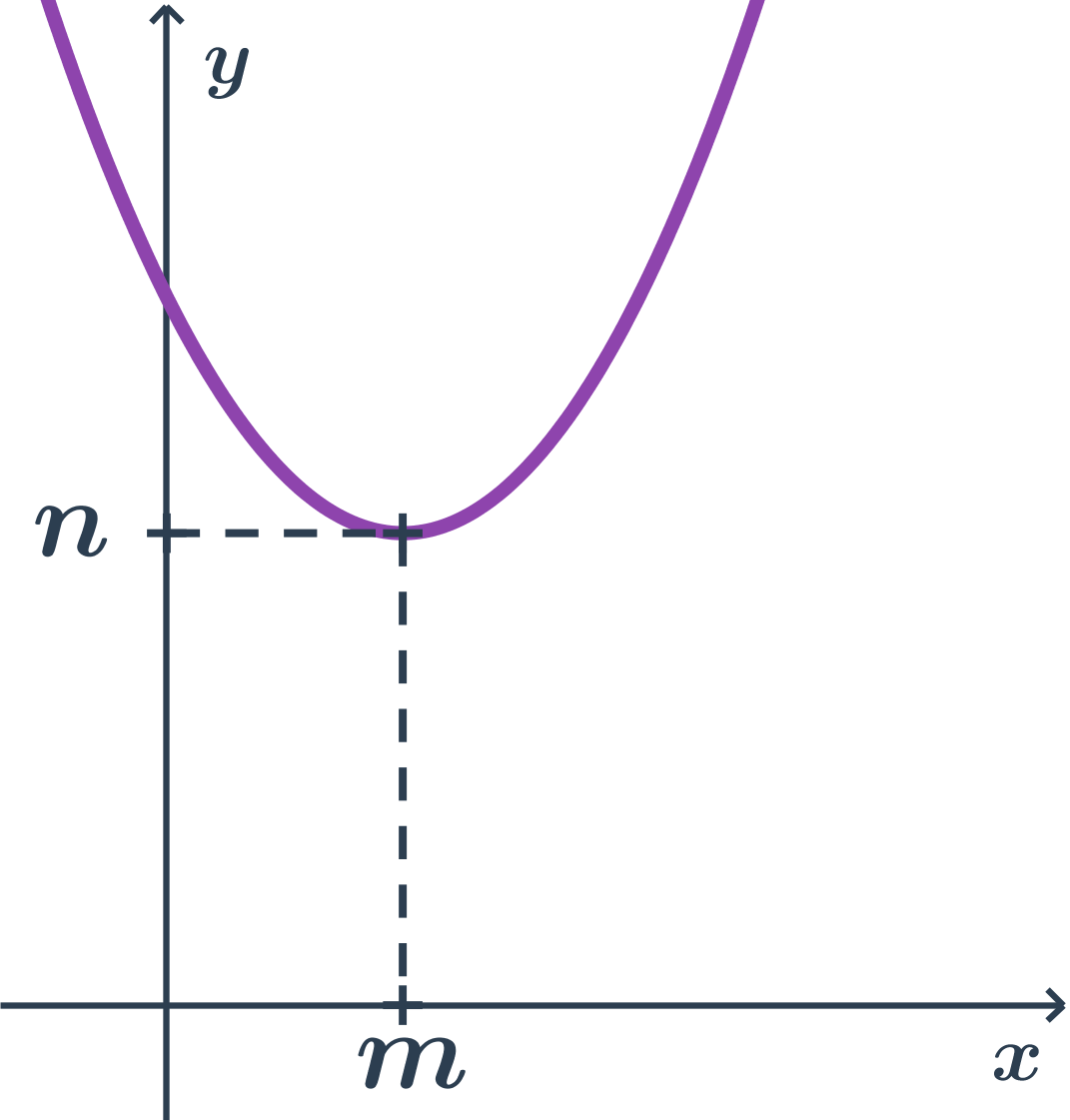
• body paraboly majú $y$ súradnicu aspoň tak veľkú ako vrchol (teda $n$)
• vrcholová rovnica: $(x-m)^2= + 2p(y-n)$

Príklad paraboly s osou rovnobežnou s osou y, druhá orientácia

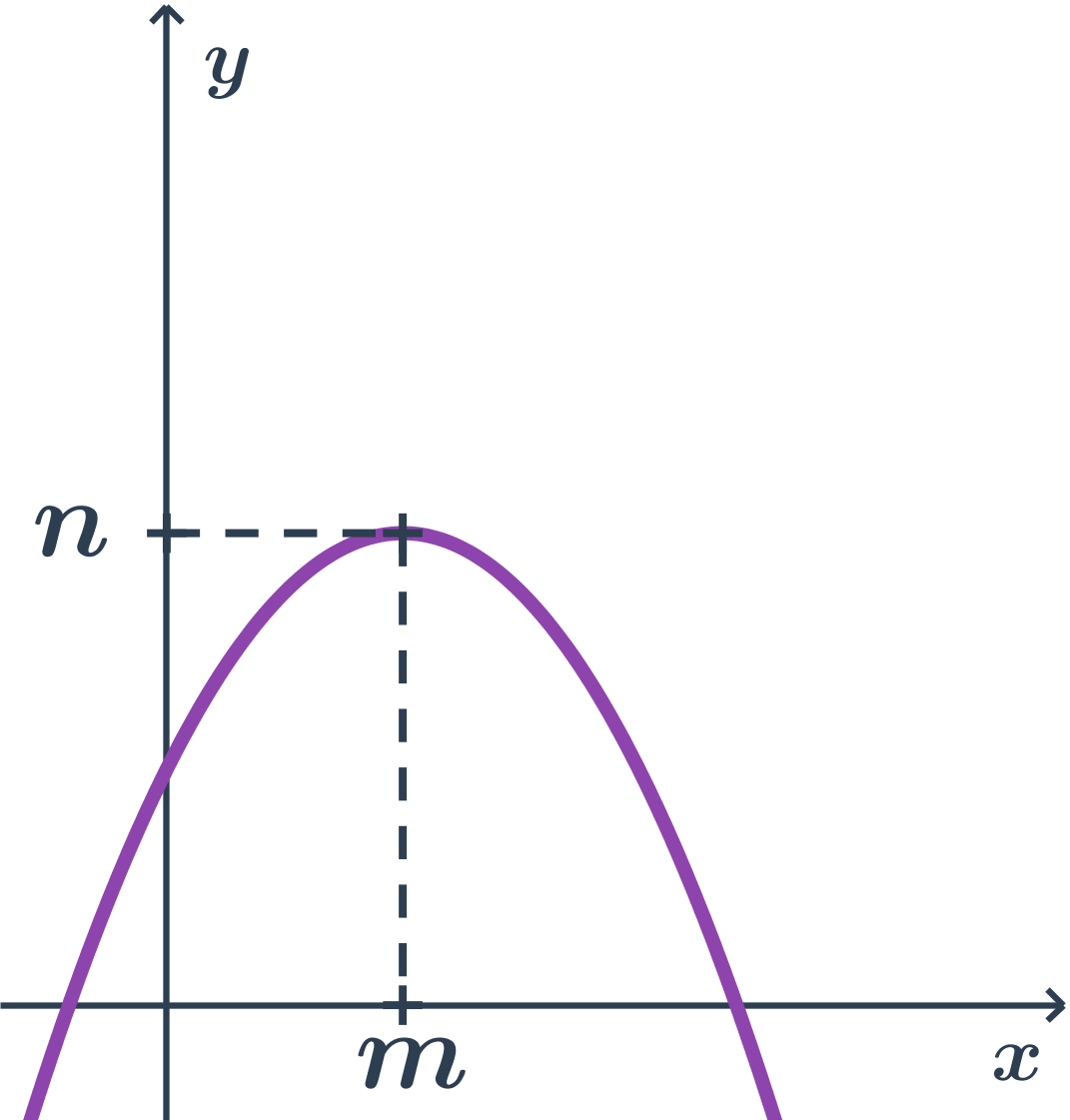
• body paraboly majú $y$ súradnicu najviac tak veľkú ako vrchol (teda $n$)
• vrcholová rovnica: $(x-m)^2= - 2p(y-n)$

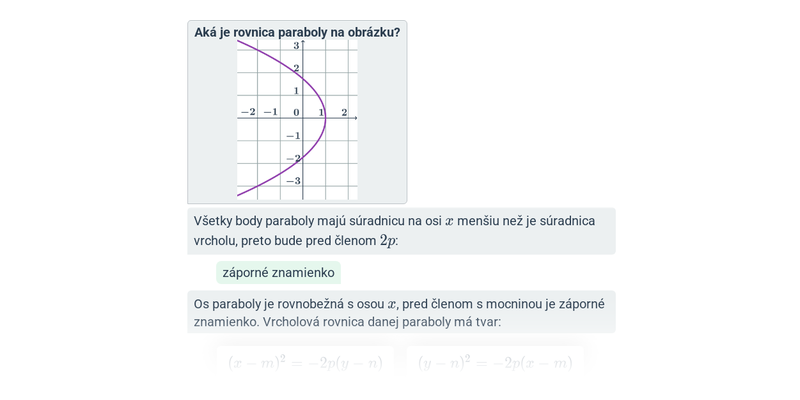
Príklad paraboly s osou rovnobežnou s osou x

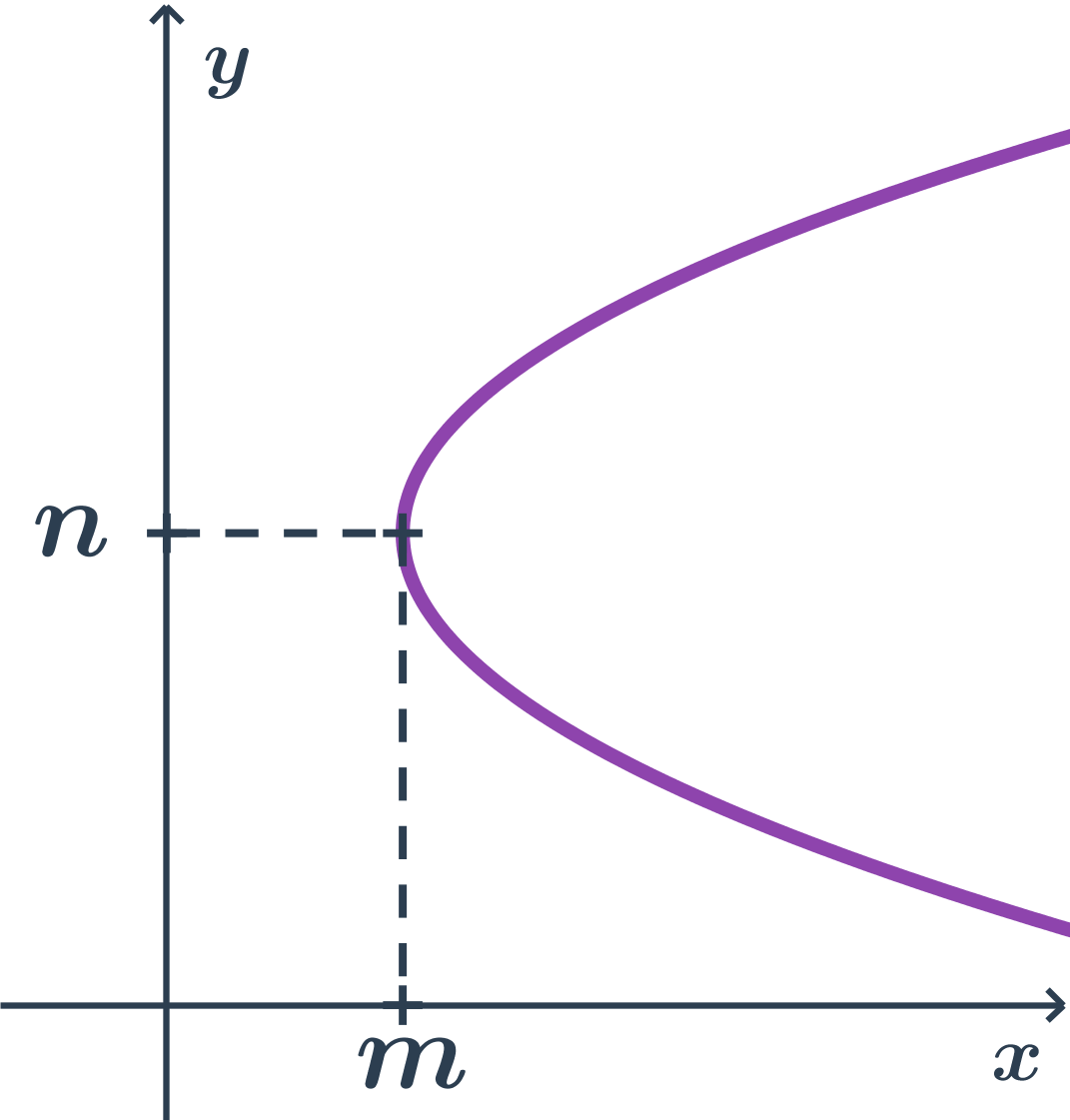
• body paraboly majú $x$ súradnicu aspoň tak veľkú ako vrchol (teda $m$)
• vrcholová rovnica: $(y-n)^2= + 2p(x-m)$

Príklad paraboly s osou rovnobežnou s osou x, druhá orientácia

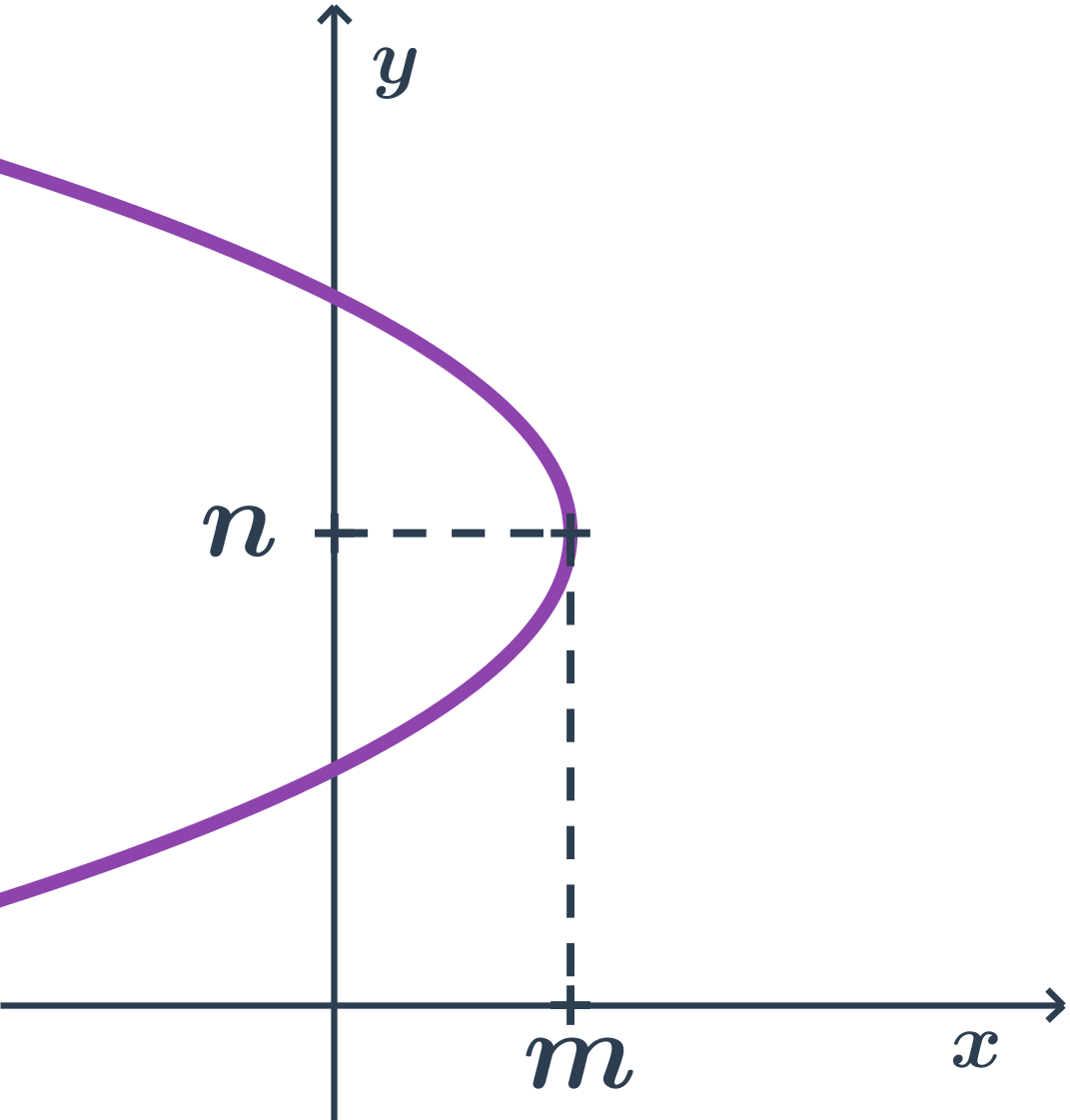
• body paraboly majú $x$ súradnicu najviac tak veľkú ako vrchol (teda $m$)
• vrcholová rovnica: $(y-n)^2= - 2p(x-m)$

Všeobecná rovnica paraboly

Tvar rovnice závisí od umiestnenia osi:

• os paraboly je rovnobežná s osou $y$: $y=ax^2+bx+c$
• os paraboly je rovnobežná s osou $x$: $x=ay^2+bx+c$

Príklad paraboly s osou rovnobežnou s osou y, všeobecná rovnica

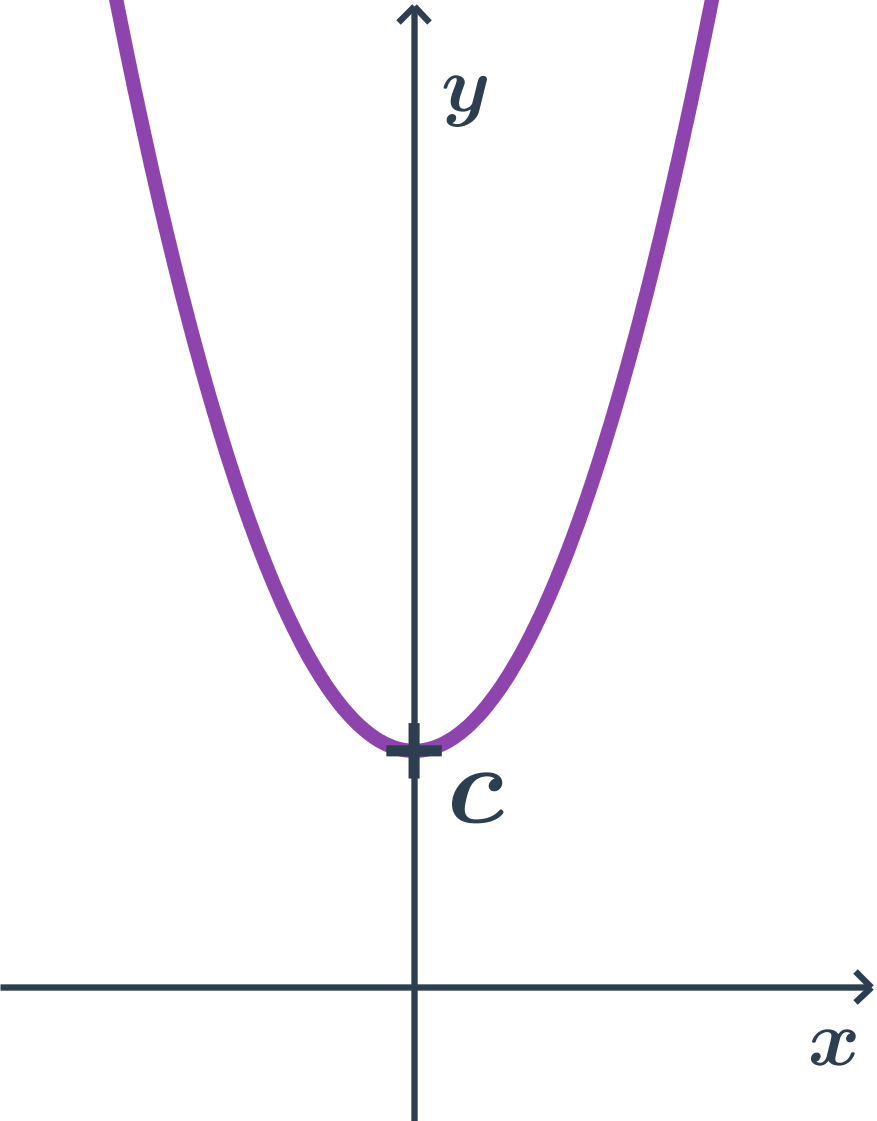
• všeobecná rovnica: $y=ax^2+bx+c$
• kde $a>0$

Príklad paraboly s osou rovnobežnou s osou y, druhá orientácia, všeobecná rovnica

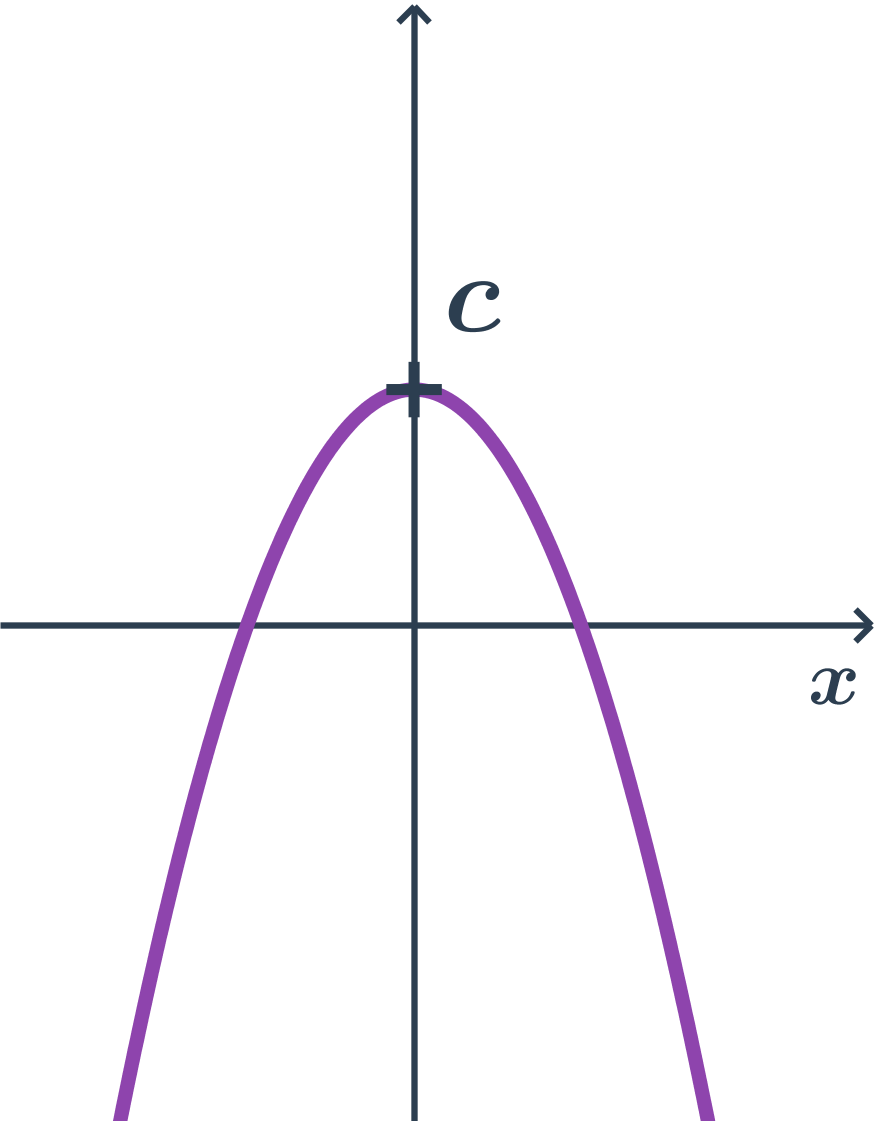
• všeobecná rovnica: $y=ax^2+bx+c$
• kde $a<0$

Príklad paraboly s osou rovnobežnou s osou x, všeobecná rovnica

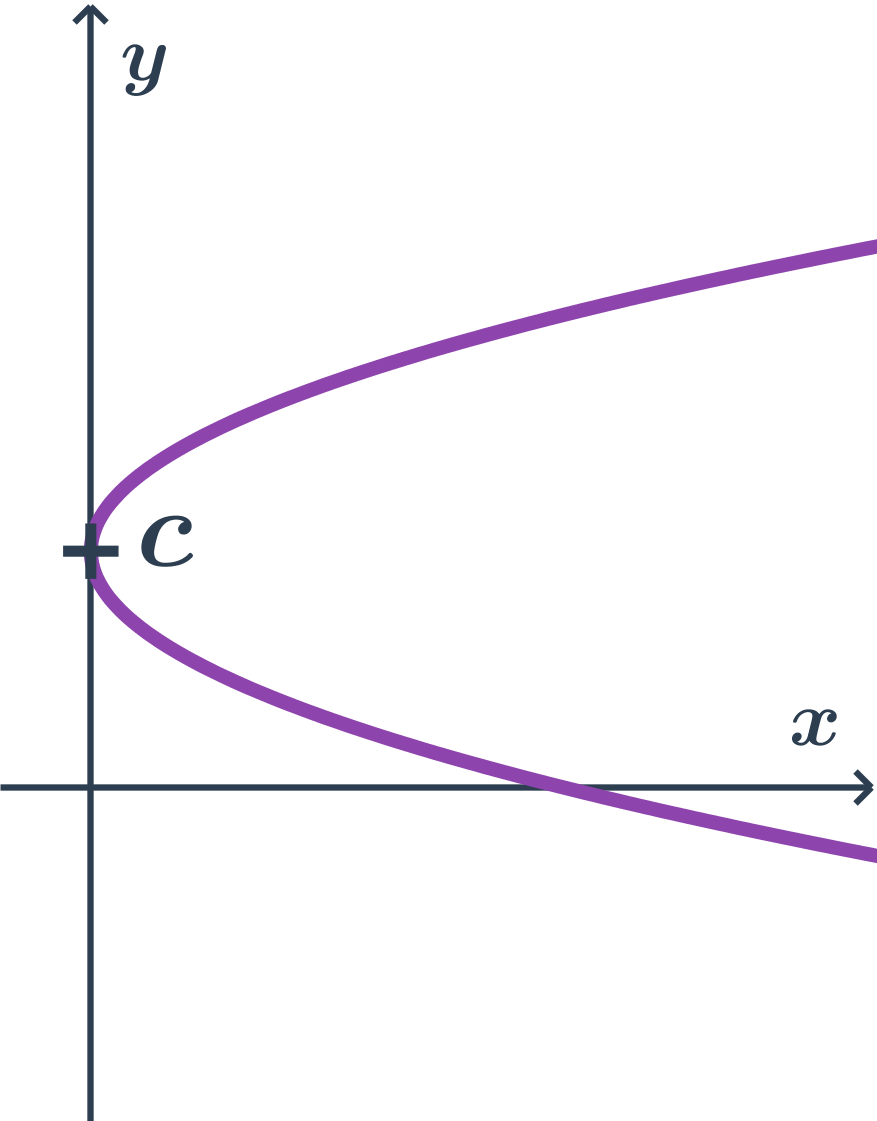
• všeobecná rovnica: $x=ay^2+bx+c$
• kde $a>0$

Príklad paraboly s osou rovnobežnou s osou x, druhá orientácia, všeobecná rovnica

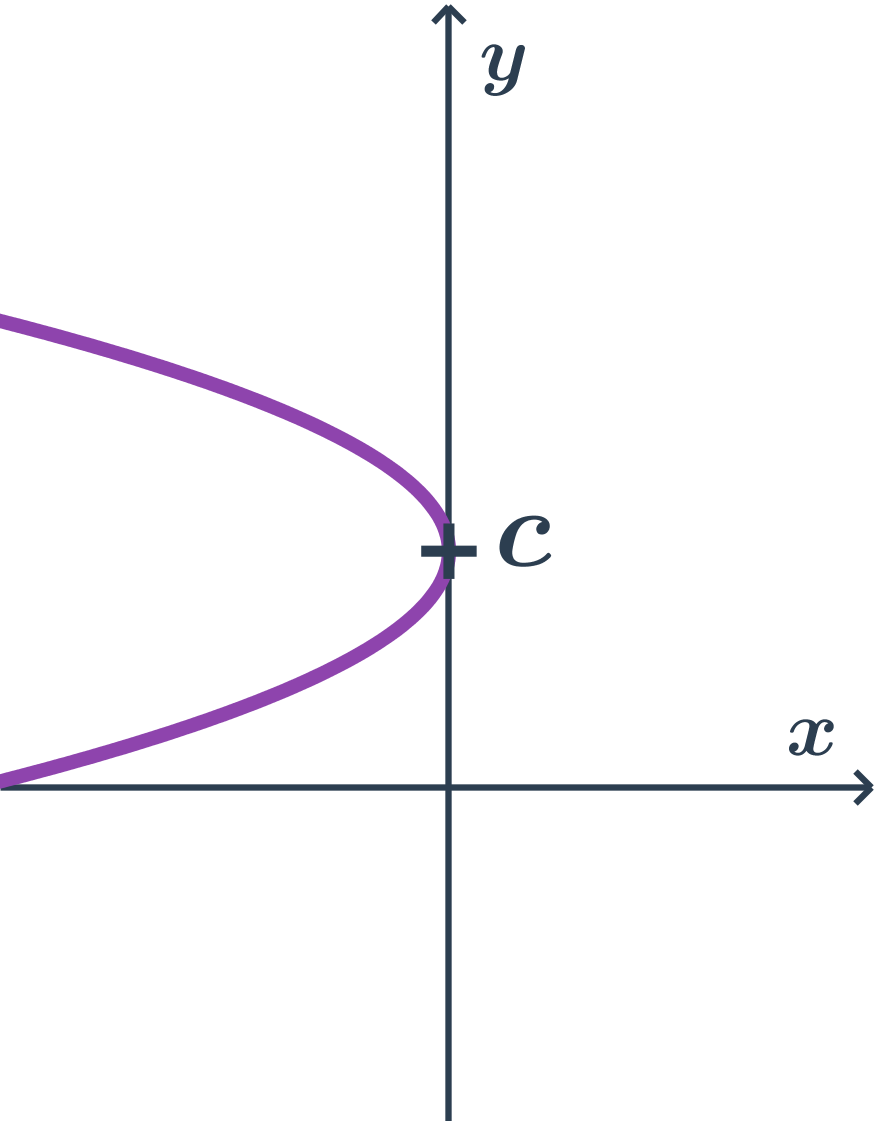
• všeobecná rovnica: $x=ay^2+bx+c$
• kde $a<0$

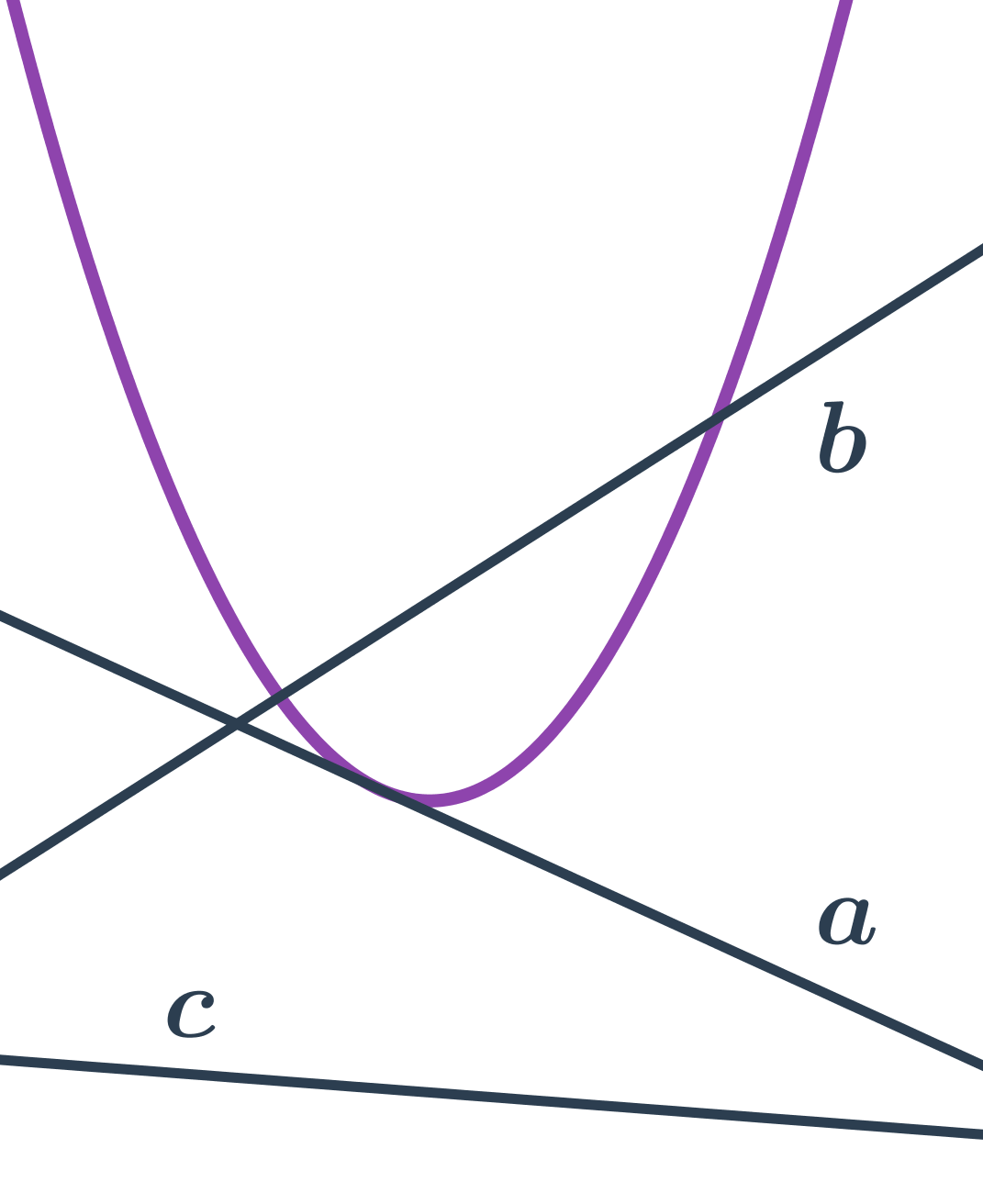
Priamka a parabola

• priamka $b$ pretína parabolu v dvoch bodoch – sečnica paraboly
• priamka $a$ sa dotýka paraboly v jednom bode – dotyčnica paraboly
• priamka $c$ nepretína parabolu

Rovnica dotyčnice paraboly v bode, ktorý leží na parabole

• parabola daná rovnicou $(x-m)^2=\pm 2p(y-n)$ má v bode $T=[x_0;y_0]$ dotyčnicu: $(x-m)(x-x_0)=\pm p(y-n)\pm p(y-y_0)$
• parabola daná rovnicou $(y-n)^2=\pm 2p(x-m)$ má v bode $T=[x_0;y_0]$ dotyčnicu: $(y-n)(y-y_0)=\pm p(x-m)\pm p(x-x_0)$

Druhý príklad dotyčnice paraboly v bode

• majme parabolu danú vrcholovou rovnicou: $(x-2)^2=-4(y-1)$
• pre túto parabolu je $m=2, n=1, p=2$
• na tejto parabole leží (súradnice spĺňajú rovnicu) napríklad bod $T=[6;-3]$
• dotyčnica danej paraboly v bode $T=[6;-3]$ má rovnicu: $(x-2)(x-6)= -2(y-1)-2(y+3)$

Vysvetlenie mi pomohlo

Vysvetlenie mi nepomohlo