Filter podľa ročníka
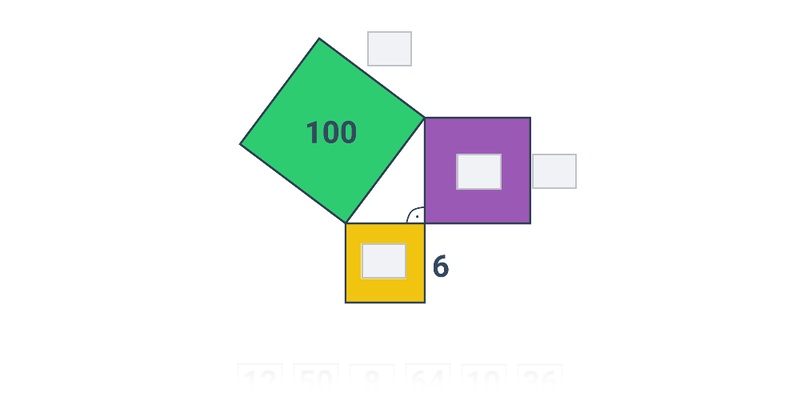
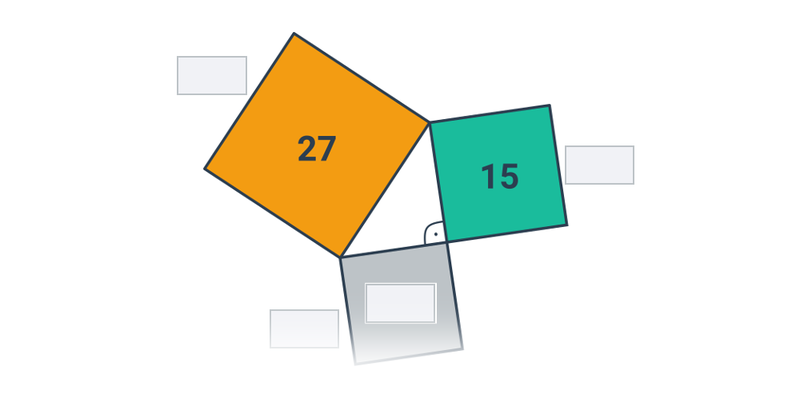
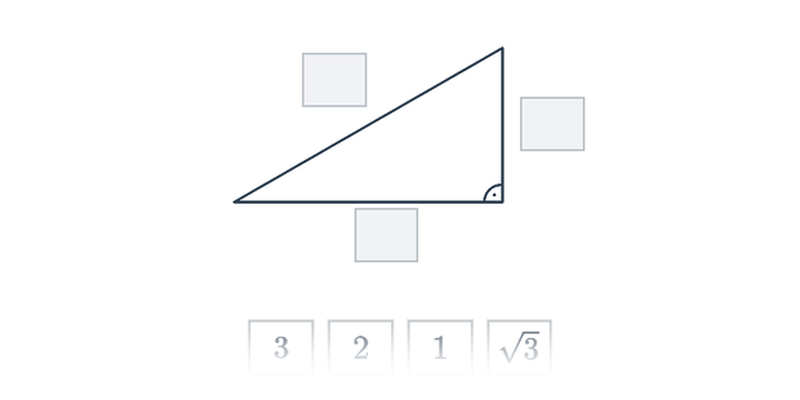
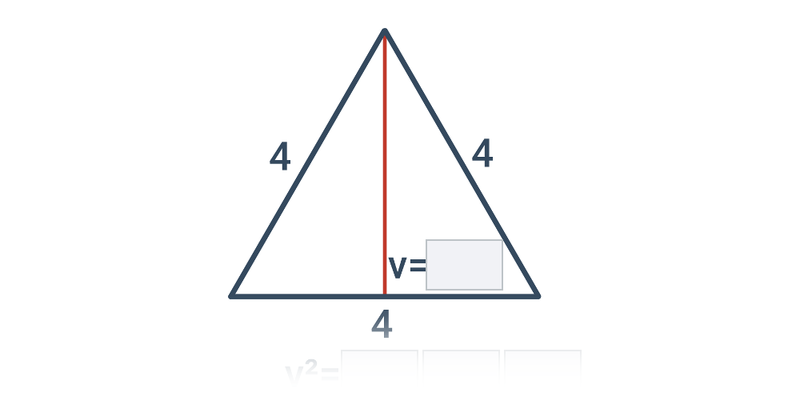
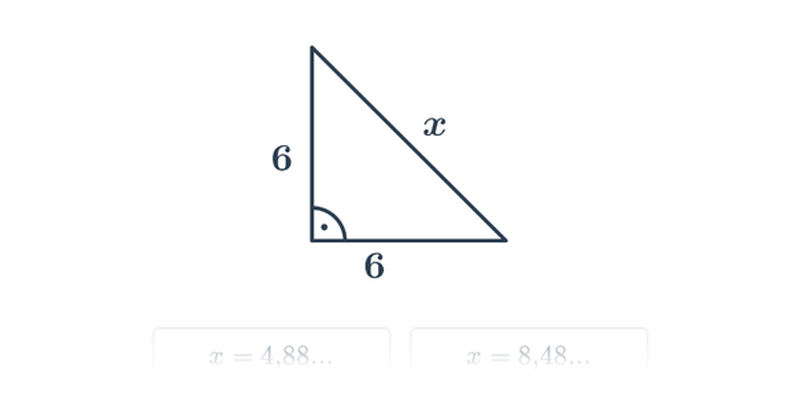
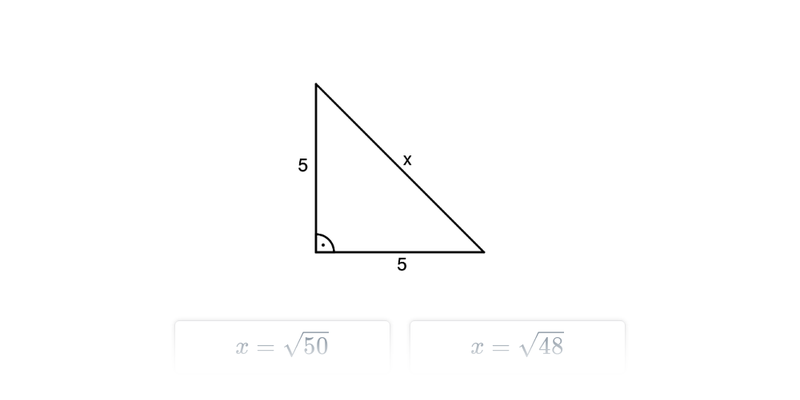
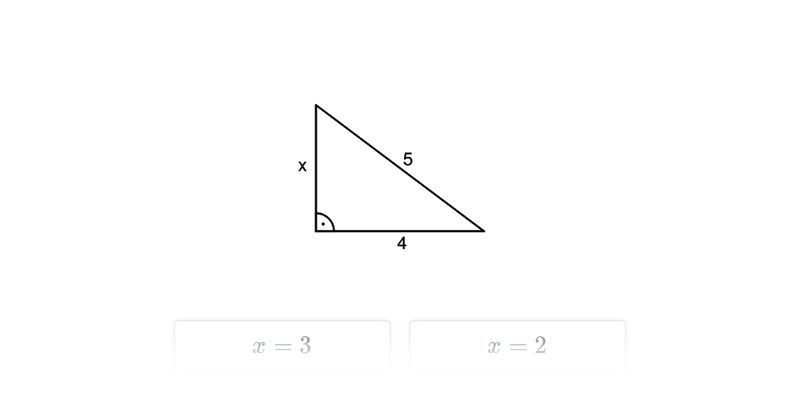
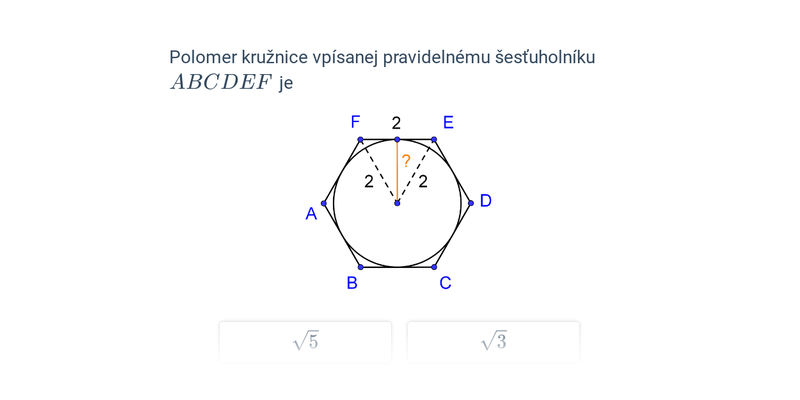
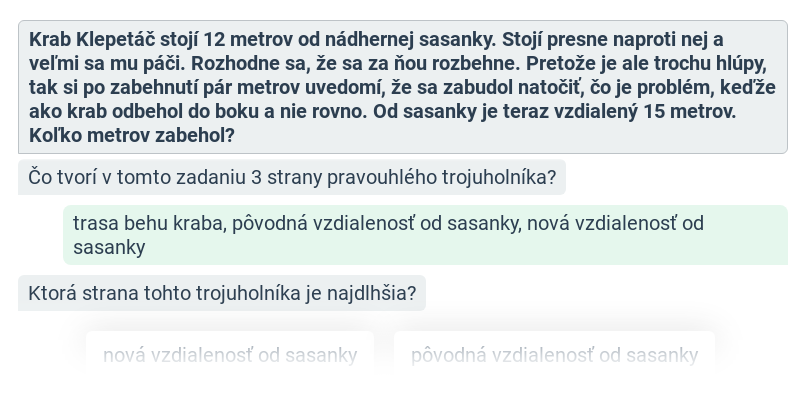
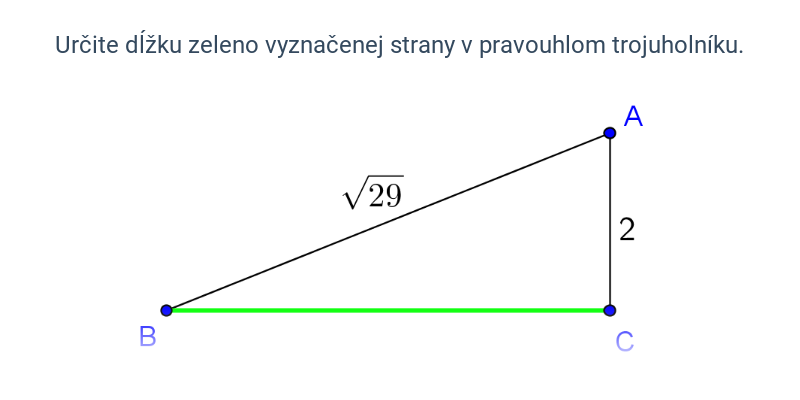
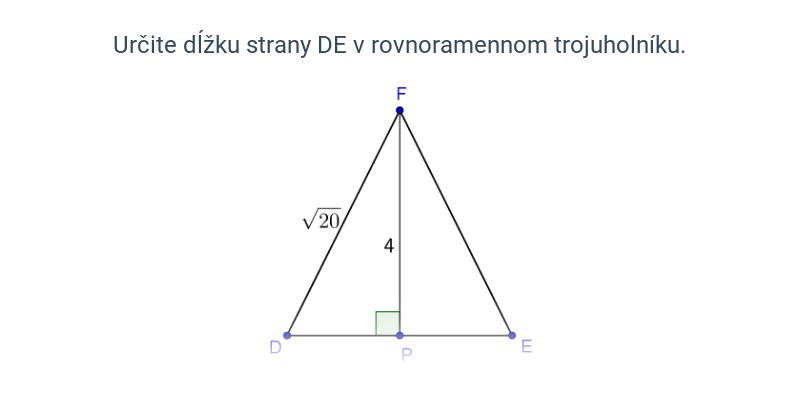
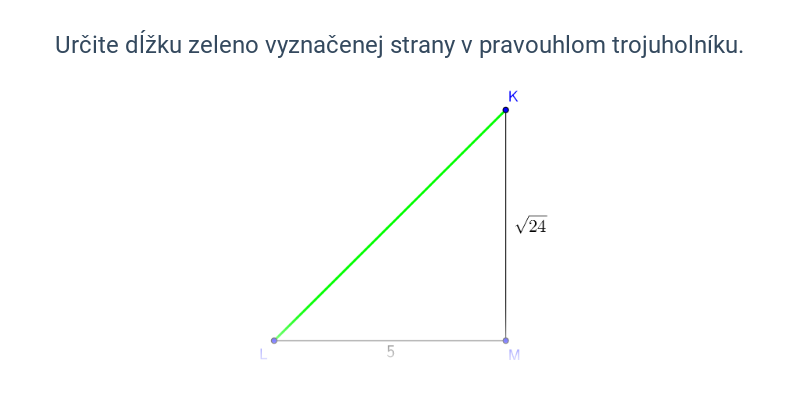
Pytagorova veta popisuje vzťah, ktorý platí medzi dĺžkami strán pravouhlého trojuholníka. Veta znie: Obsah štvorca zostrojeného nad preponou pravouhlého trojuholníka je rovný súčtu obsahov štvorcov nad obomi jeho odvesnami. Pytagorovu vetu môžeme zapísať vzťahom c^2 = a^2 + b^2, kde c označuje dĺžku prepony pravouhlého trojuholníka a dĺžky odvesien sú a, b.
Nasledujúci obrázok znázorňuje graficky znenie vety a tiež „obrázkový dôkaz“ tejto vety:
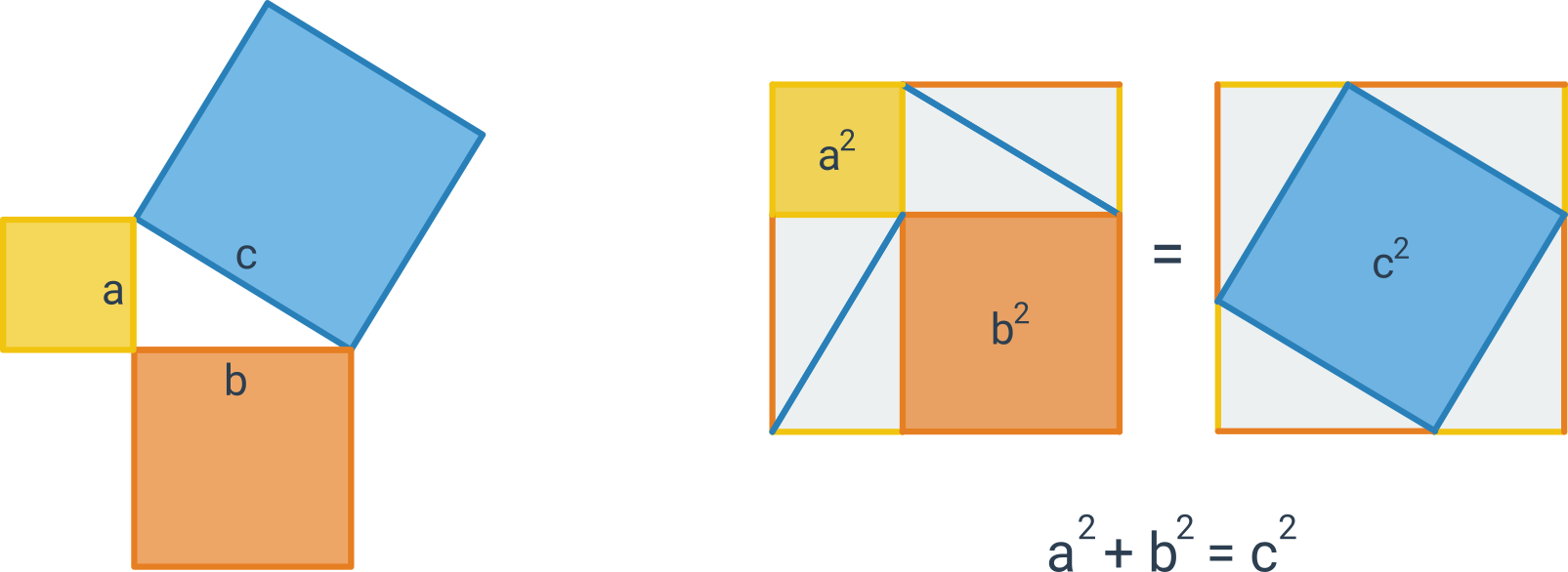
Platí aj opačný smer: Ak má trojuholník strany dĺžok a, b, c, ktoré spĺňajú rovnosť c^2 = a^2 + b^2, potom musí ísť o pravouhlý trojuholník s preponou c.
Presúvanie
Presúvanie kartičiek na správne miesto. Jednoduché ovládanie, zaujímavé a neotrepané úlohy.
Pytagorova veta: základné použitie (ľahké) • FLC
Typicky zaberie: 8 min.
Pytagorova veta: základné použitie (stredné) • FGE
Typicky zaberie: 11 min.
Pytagorova veta: základné použitie (ťažké) • G2U
Typicky zaberie: 5 min.
Pytagorova veta: aplikácie (stredné) • FR9
Typicky zaberie: 9 min.
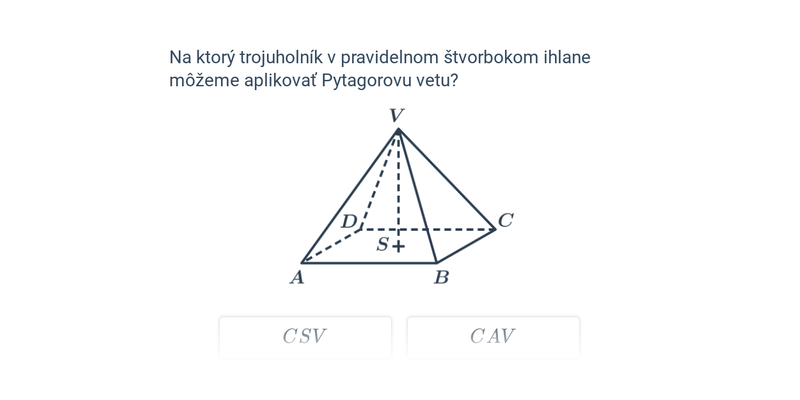
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Pytagorova veta: základné použitie (ľahké) • GW3
Typicky zaberie: 6 min.
Pytagorova veta: základné použitie (stredné) • EC1
Typicky zaberie: 7 min.
Pytagorova veta: základné použitie (ťažké) • FPD
Typicky zaberie: 9 min.
Pytagorova veta: aplikácie (ťažké) • FNT
Typicky zaberie: 5 min.
Pytagorova veta: aplikácie v 3D (ťažké) • FPF
Typicky zaberie: 5 min.
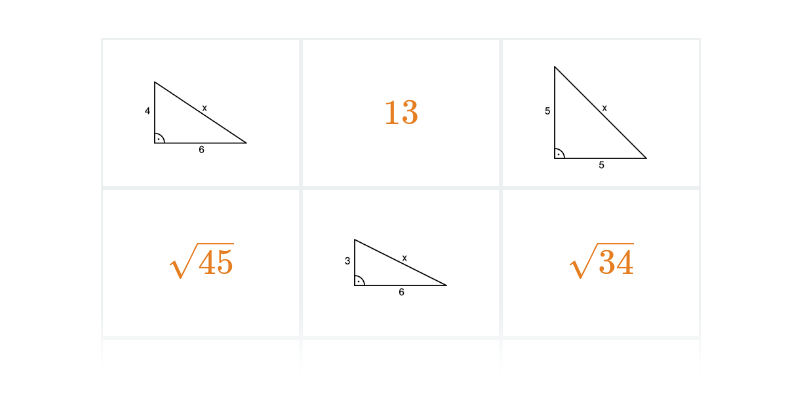
Pexeso
Hľadanie dvojíc, ktoré k sebe patria.
Pytagorova veta: základné použitie (stredné) • E4K
Typicky zaberie: 7 min.
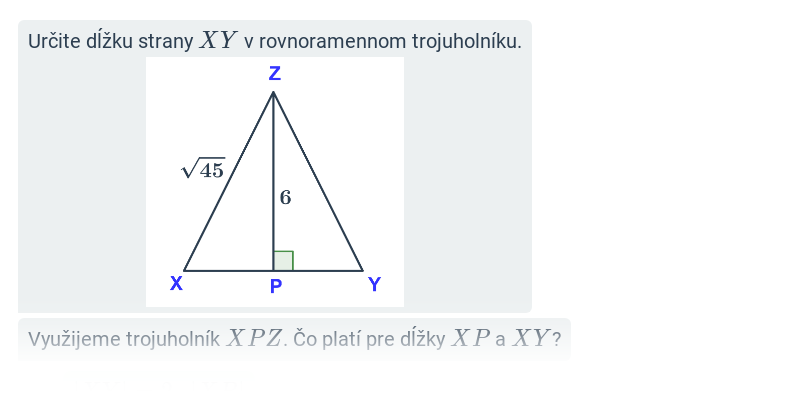
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
Pytagorova veta: aplikácie (stredné) • E31
Typicky zaberie: 10 min.
Pytagorova veta: aplikácie (ťažké) • FS6
Typicky zaberie: 5 min.
Pytagorova veta: slovné úlohy po krokoch (stredné) • FHA
Typicky zaberie: 17 min.
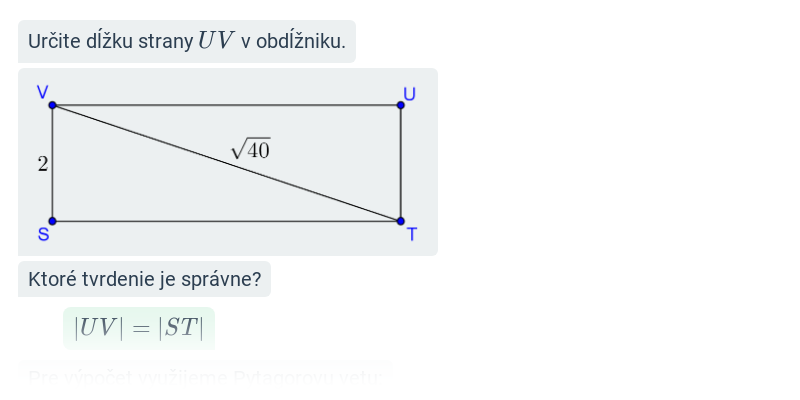
Počítanie
Cvičenie, v ktorom píšete odpoveď na klávesnici.
Pytagorova veta: základné použitie (stredné) • EKZ
Typicky zaberie: 11 min.
Pytagorova veta: aplikácie (stredné) • ELV
Typicky zaberie: 7 min.
Pytagorova veta: mix (stredné) • E4B
Typicky zaberie: 13 min.
Slovné úlohy
Klasické precvičovanie slovných úloh s pestrou ponukou zadaní a vysvetľujúcimi textami.
Pytagorova veta: aplikácie (stredné) • EJ2
Typicky zaberie: 13 min.
Pytagorova veta: aplikácie (ťažké) • E29
Typicky zaberie: 10 min.
Pytagorova veta: úlohy s diagramom (ťažké) • FE3
Typicky zaberie: 5 min.
Mriežkovaná
Úloha na precvičenie geometrie s jednoduchým ovládaním a zaujímavými úlohami.
Pytagorova veta: aplikácie
Porozumenie
Čítanie textov, odpovedanie na otázky testujúce porozumenie textu.
