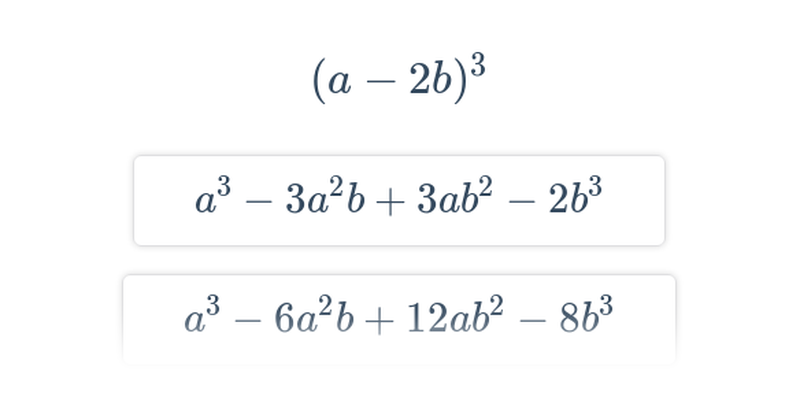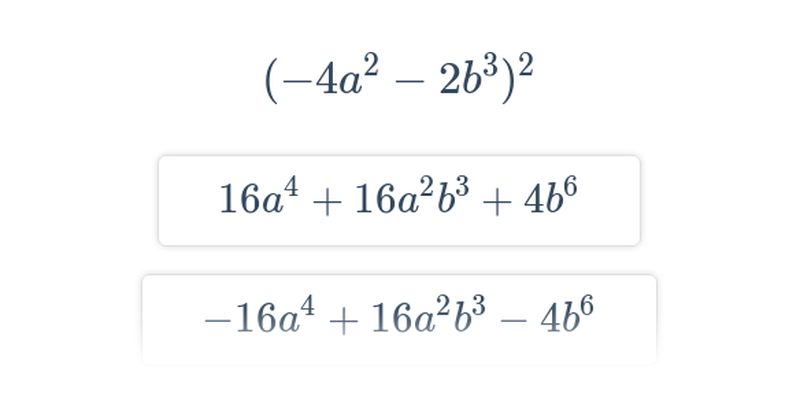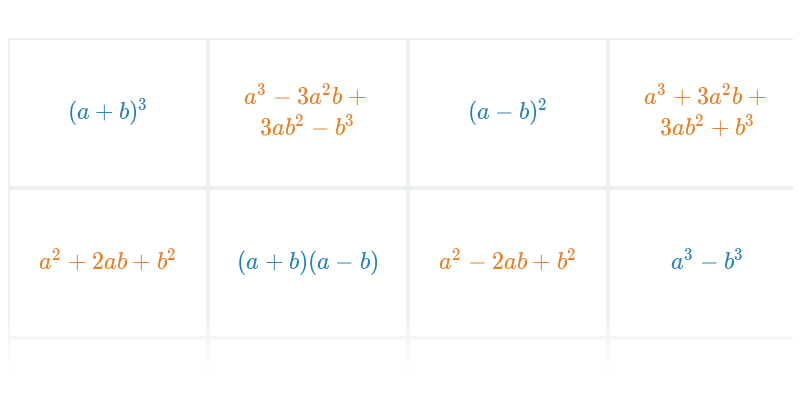Vykonávame také úpravy výrazov, ktoré zachovávajú hodnotu výrazu pre všetky možné dosadenia za premenné. Príklady úprav:
| Popis | Výraz | Upravený výraz |
|---|---|---|
| Sčítanie členov s rovnakou premennou | 3x+2y+4x | =7x+2y |
| Roznásobenie zátvorky | x(y-2) | =xy-2x |
| Vytknutie | 4x-x^2y+3 | =x(4-xy)+3 |
| Umocnenie | (a+b)^2 | =(a+b)(a+b)=a^2+2ab+b^2 |
| Roznásobenie dvoch zátvoriek | (a+b)(a-b) | =(a+b)(a-b)=a^2+ab-ab-b^2 = a^2-b^2 |
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Úpravy výrazov: vnorené mocniny
Rozklad na súčin
Pexeso
Hľadanie dvojíc, ktoré k sebe patria.
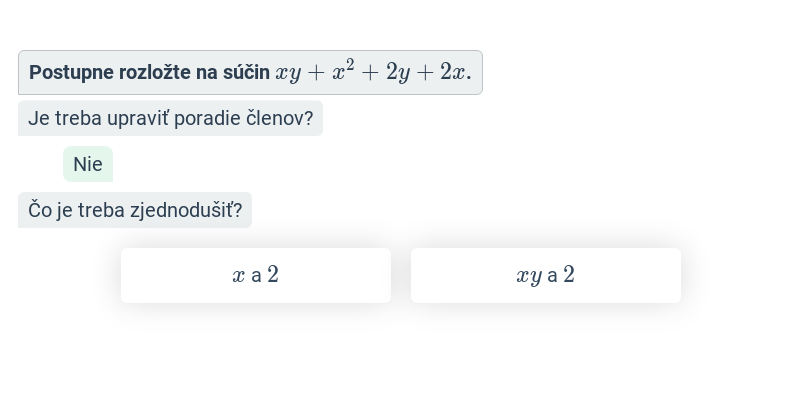
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
Rozklad na súčin
Rozklad na súčin (postupné vytýkanie)
Počítanie
Cvičenie, v ktorom píšete odpoveď na klávesnici.