Podmienky lomených výrazov

GXH

viemeto.eu/GXH

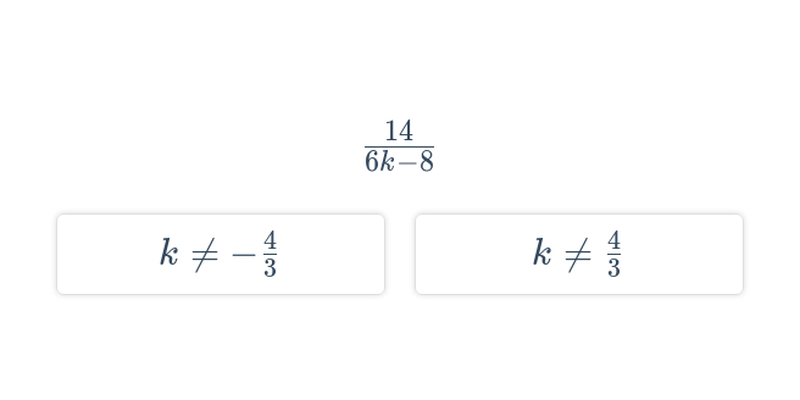
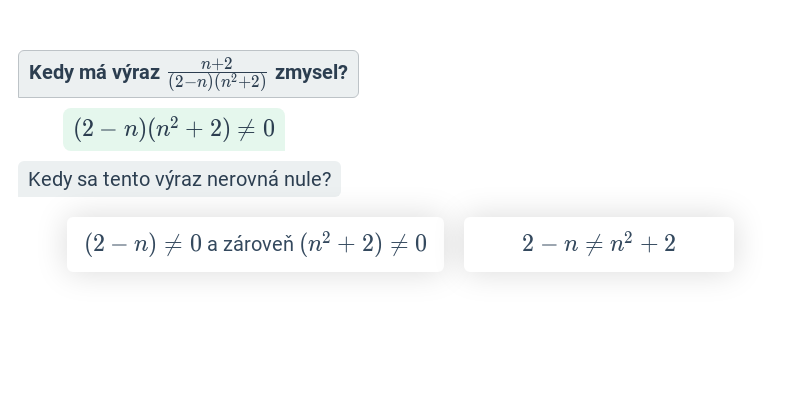
V prípade lomených výrazov je treba brať do úvahy podmienky, pre ktoré má zmysel. Lomený výraz má zmysel pre všetky hodnoty premenných, pre ktoré je výraz v menovateli iný ako nula. Príklady:

Výraz \frac{x+5}{x-3} má zmysel pre x \neq 3.
Výraz \frac{x^3}{x^2-1} má zmysel pre x \in \mathbb{R} \setminus \{-1, 1\}, pretože x^2-1 = 0 pre hodnoty -1 a 1.
Výraz \frac{x^3}{x^2+1} má zmysel pre všetky reálne čísla, pretože x^2+1 je vždy väčšie než nula.

Určiť, kedy je výraz iný ako nula, nemusí byť úplne ľahké. Na ilustráciu uveďme ťažší príklad výrazu s všeobecným kvadratickým menovateľom (môžu sa hodiť poznatky z kvadratických rovníc a grafy kvadratických funkcií).

Určenie podmienok lomeného výrazu \frac{1}{x^2+kx+3}

Výraz má zmysel ak x^2+kx+3 \neq 0.
Diskriminant kvadratickej rovnice x^2+kx+3 = 0 pre premennú x je k^2-12.
Uvedená kvadratická rovnica má jedno alebo dve riešenia x_1=\frac{-k+\sqrt{k^2-12}}{2}, x_2=\frac{-k-\sqrt{k^2-12}}{2} pre k^2-12 \geq 0, teda pre k \leq -\sqrt{12} alebo k \geq \sqrt{12}.
Lomený výraz má zmysel, keď jeho menovateľ nie je rovný nule, teda keď nemá kvadratická rovnica žiadne riešenie alebo x nie je rovno riešenie tejto rovnice.
Celkovo má výraz \frac{1}{x^2+kx+3} zmysel keď k \in (-\sqrt{12},\sqrt{12}) nebo x \notin \{ x_1,x_2\}.

Určenie podmienok lomeného výrazu \frac{1}{\frac{x-3}{x}}

Výraz má zmysel, ak žiadny zlomok nemá nulový menovateľ.
Ide o zlomok \frac{1}{\frac{x-3}{x}} s menovateľom \frac{x-3}{x} a tiež o zlomok \frac{x-3}{x} s menovateľom x.
\frac{x-3}{x} by bolo rovné nule pre x=3.
x by bolo rovné nule priamo pre x=0.
Takže celkovo podmienky, za ktorých má zmysel výraz zo zadania, sú: x \neq 3, x \neq 0