Výpis prehľadov
Obsah a obvod
Podkapitoly
Obsah a obvod
Obsah značíme S. Obsah vyjadruje, koľko „miesta v rovine“ útvar zaberá. Meria sa v jednotkách obsahu.
Obvod značíme o. Obvod je súčet dĺžok čiar, ktoré útvar vymedzujú. Obvod sa meria v jednotkách dĺžky.
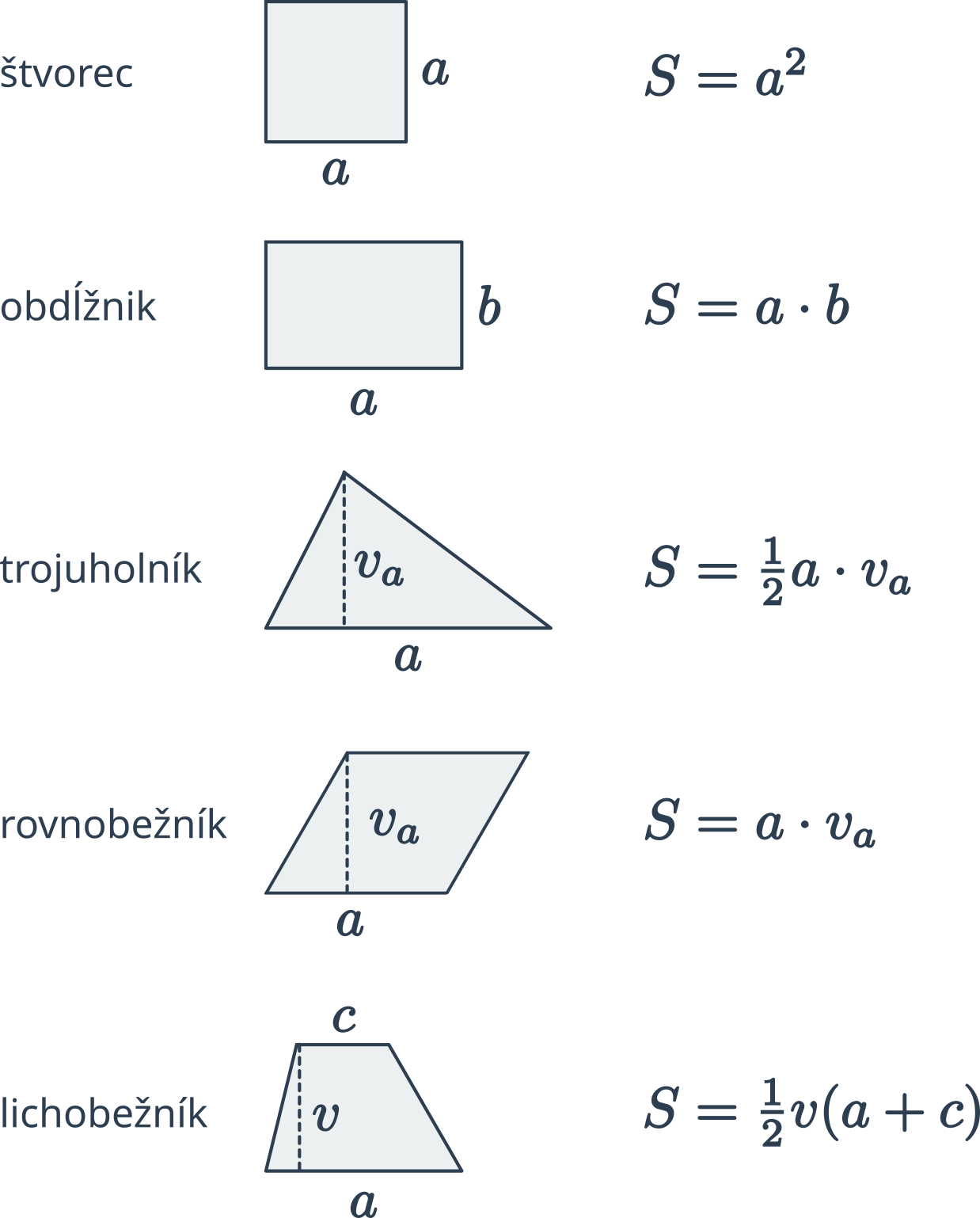
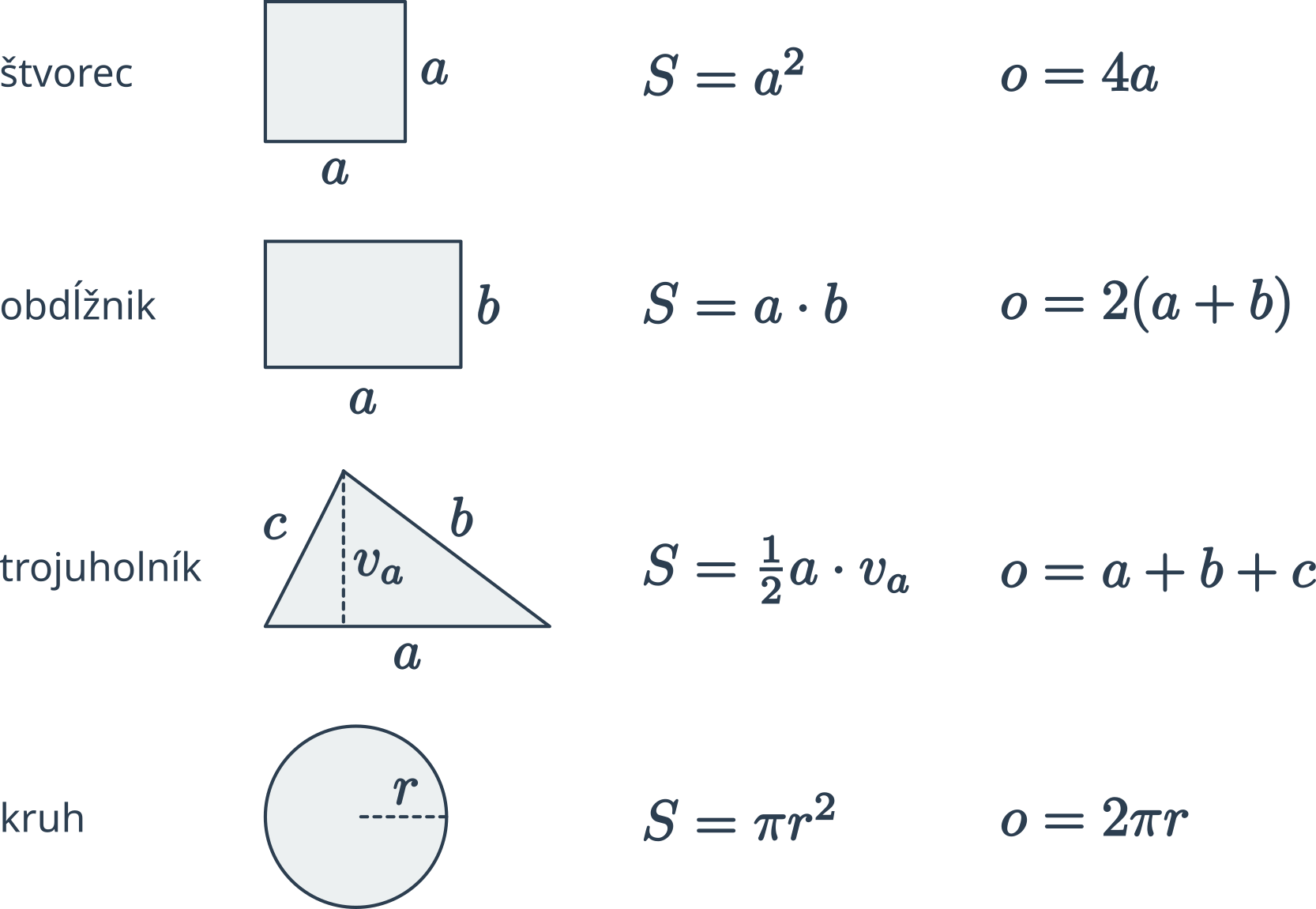
Prehľad vzorcov pre obsah a obvod základných geometrických útvarov:
Obvod trojuholníka
Obvod trojuholníka vypočítame ako súčet dĺžok jeho strán: o=a+b+c
Príklad:
Trojuholník na obrázku má dĺžky strán a=10, b=8, c=14, takže jeho obvod je o=a+b+c=10+8+14=32.
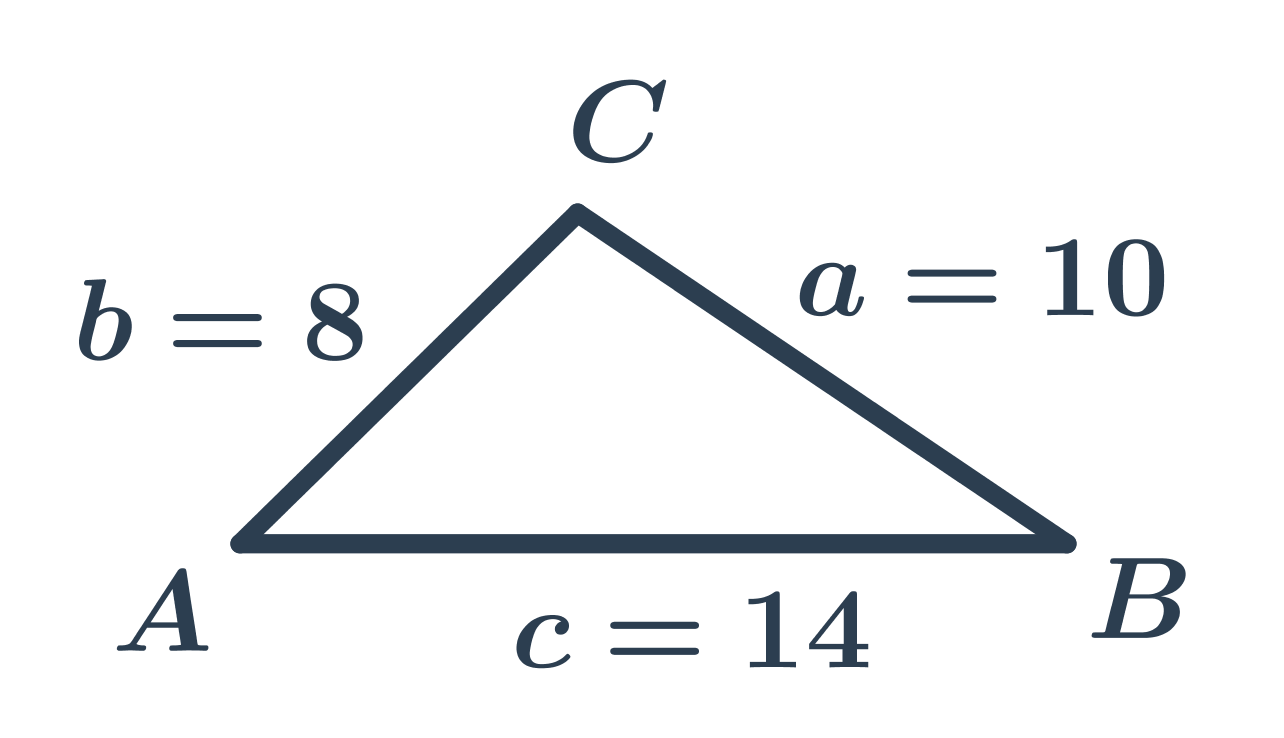
Obvod štvorca a obdĺžnika
Obvod štvorca so stranou s dĺžkou a je o=a+ a+a+a= 4a.
Obvod obdĺžnika so stranami s dĺžkami a,b je rovný o=a + b + a + b = 2\cdot (a+b).
HoreObvod rovnobežníka
Obvod rovnobežníka so stranami s dĺžkami a,b je rovný S=a + b + a + b = 2\cdot (a+b).
HoreObvod lichobežníka
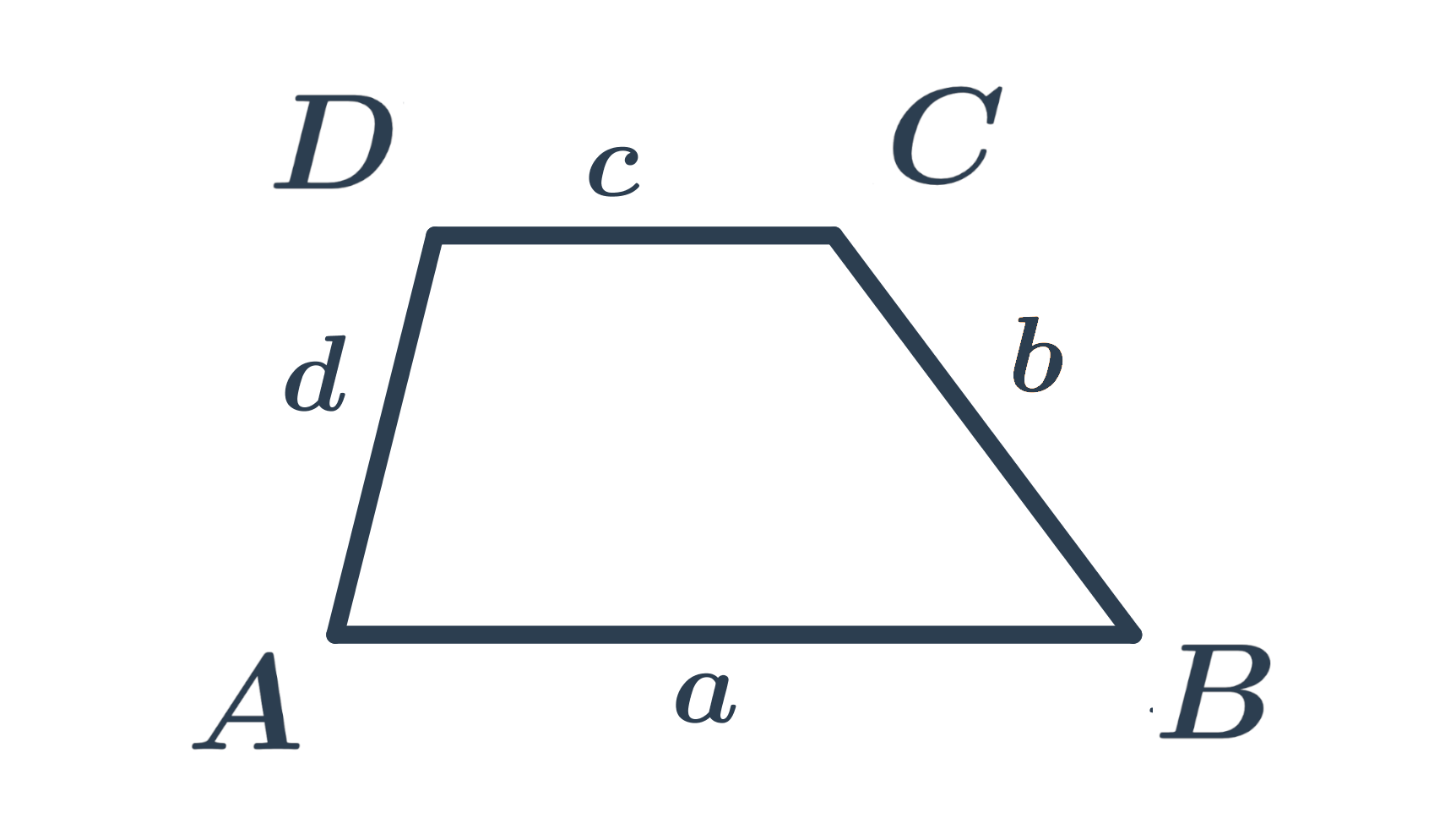
Obvod lichobežníka je súčet dĺžok jeho strán. Teda obvod lichobežníka ABCD so stranami s dĺžkami a,b,c,d vypočítame podľa vzorčeka o=a+b+c+d.
Obvod kruhu, dĺžka kružnice
Vzorec pre obvod kruhu
Obvod kruhu (aj kružnice) s polomerom r je o=2\pi r. Pre priemer d platí o = \pi d.
Konštanta \pi sa tiež nazýva Ludolfovo číslo. \pi je iracionálne číslo, čo znamená, že nejde vyjadriť zlomkom ani zapísať presne v desiatkovej sústave. Približná hodnota \pi je 3,141 592 65.
Pri výpočte obvodu kruhu dávame dobrý pozor na to, či vychádzame zo znalosti polomeru alebo priemeru. Zámena priemeru za polomer je častou chybou.
Intuícia
Základnú intuíciu za vzorcom pre výpočet obvodu kruhu približuje nižšie uvedený obrázok. Obvod oranžového štvorca je 8\cdot r. Obvod kruhu je „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Príklady
- Majme kruh s polomerom 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm.
- Kružnica s priemerom 2 cm má dĺžku \pi \cdot 2 \approx 6,3 cm.
- Stredový kruh na futbalovom ihrisku má polomer 9{,}1 metra. Ak ho chceme obísť po jeho okrajovej čiare, prejdeme 2 \pi \cdot 9{,}1 \approx 57 metrov.
Dĺžka oblúka
Dĺžka oblúka
Dĺžku oblúka, ktorý na kružnici s polomerom r zodpovedá stredovému uhlu \alpha vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Príklady
- Dĺžka oblúka na obrázku je: \frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
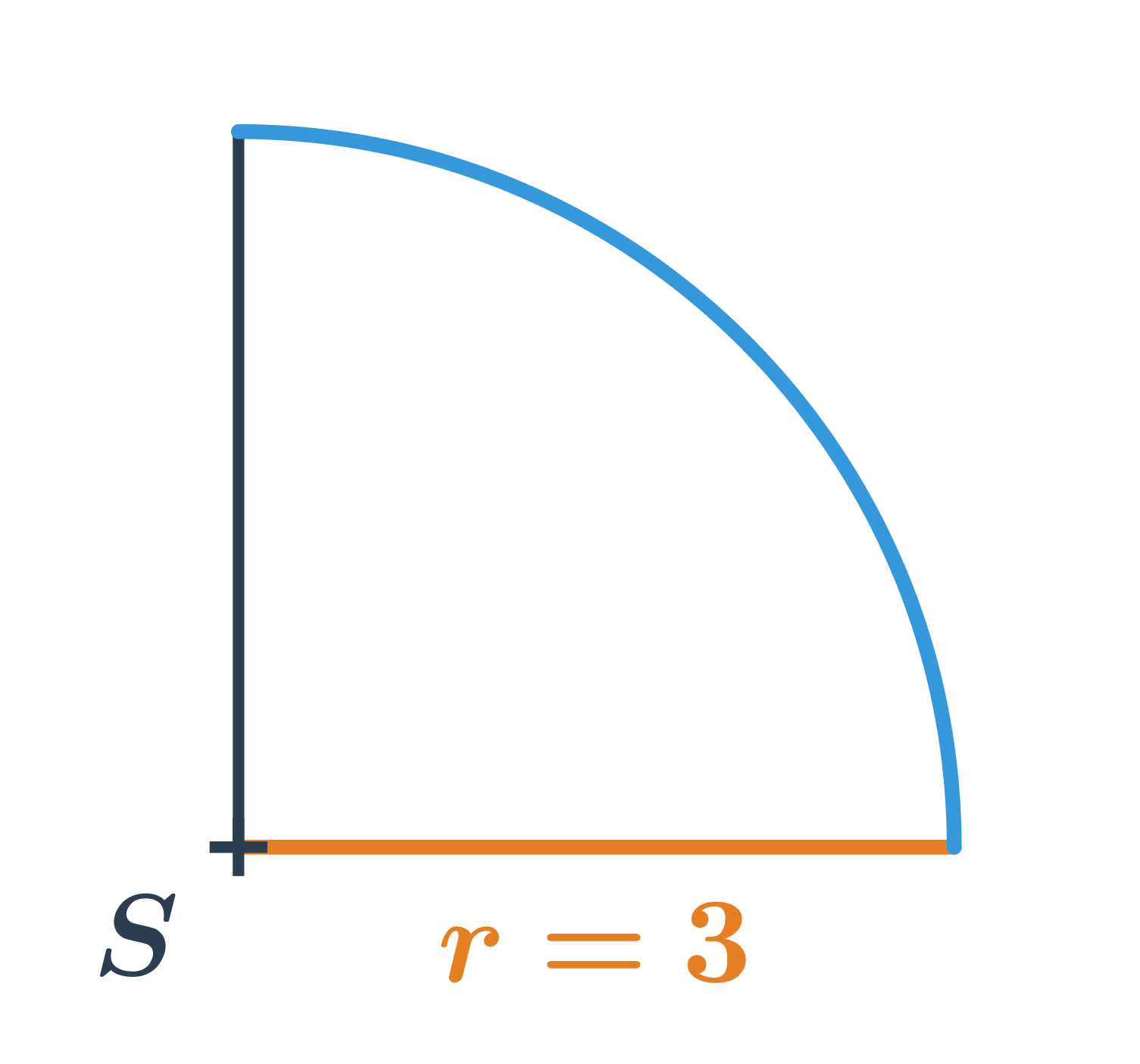
- Dĺžka celej kružnice (teda pre celých 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r
Obvod: mix
Obvod trojuholníkov a štvoruholníkov je jednoducho súčet dĺžok ich strán.
| Útvar | Vlastnosti | Obvod |
|---|---|---|
| trojuholník | strany a, b, c | o = a + b + c |
| štvorec | strana a | o = 4a |
| obdĺžnik | strany a, b | o = 2(a+b) |
| rovnobežník | strany a, b | o = 2(a+b) |
| všeobecný štvoruholník | strany a, b, c, d | o = a+b+c+d |
Obsah trojuholníka
Obsah trojuholníka vypočítame ako súčin dĺžky ľubovoľnej strany trojuholníka a výšky príslušnej k tejto strane, takže: S_{\triangle} = \frac12 \cdot a \cdot v_a = \frac12 \cdot b \cdot v_b = \frac12 \cdot c \cdot v_c
Čo si môžeme predstaviť ako polovicu obsahu obdĺžnika, v ktorom je náš trojuholník takto vpísaný:
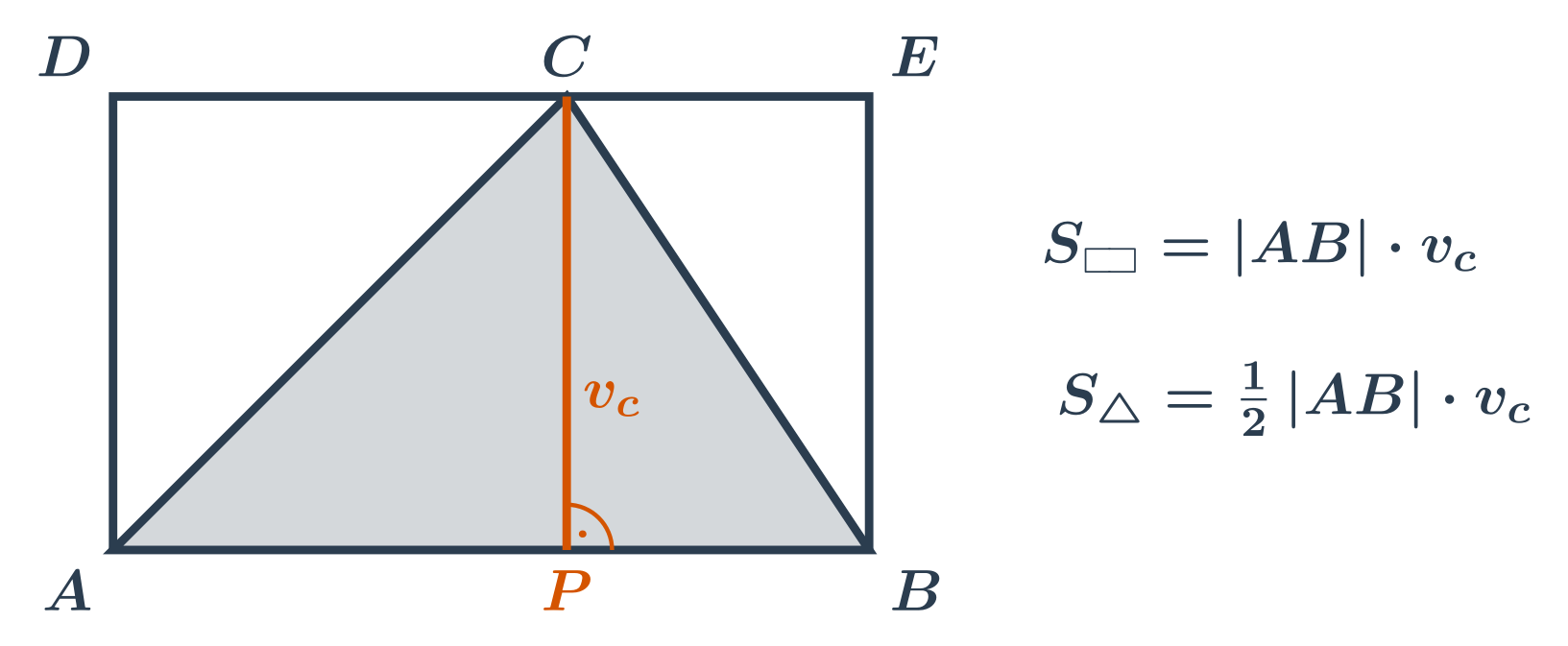
Príklady k obsahu:
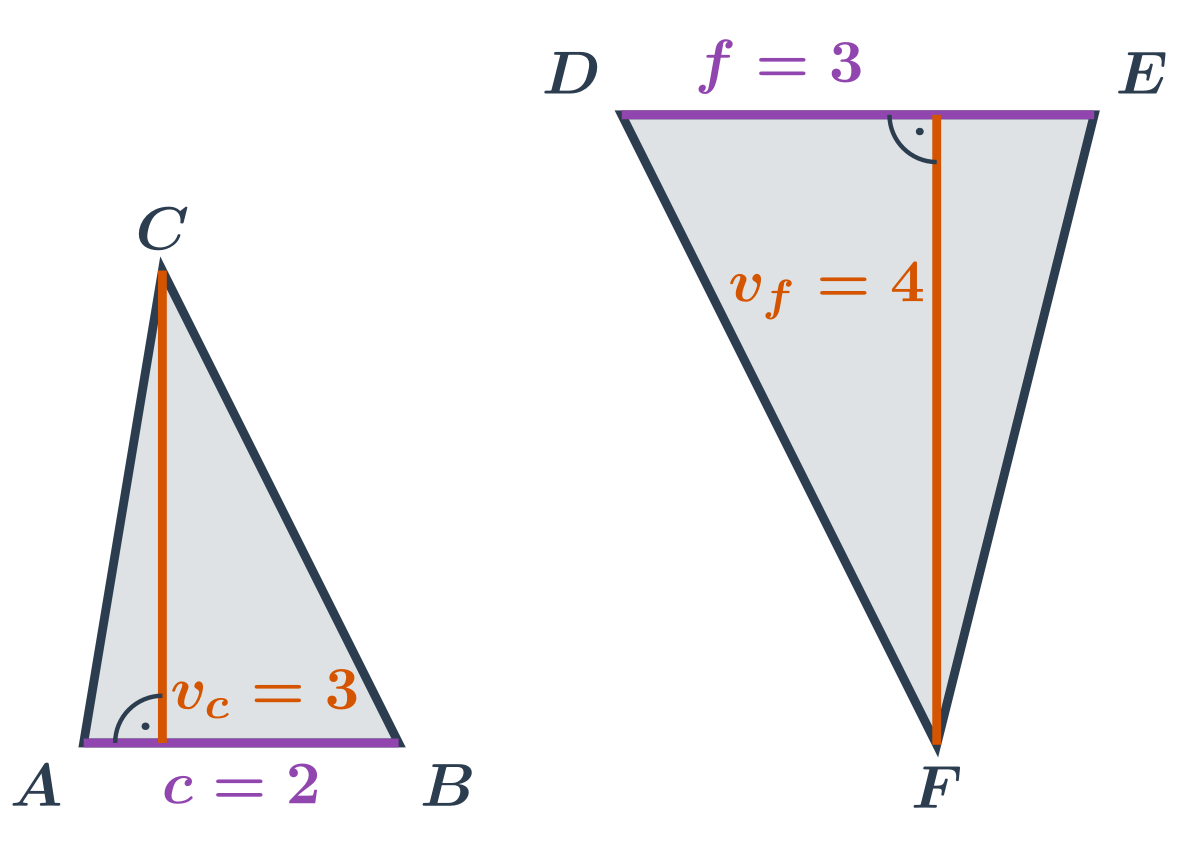
- Trojuholník ABC: Dĺžka strany \left| AB \right| je 2. Veľkosť k nej príslušnej výšky v_c je 3. Obsah trojuholníka ABC je rovný \frac12 \cdot 2 \cdot 3 = 3.
- Trojuholník DEF: Nevadí nám, že trojuholník na náčrtku vyzerá zvláštne natočený. Poznáme dĺžku strany \left| DE \right|, čo je 3. Veľkosť k nej príslušnej výšky v_f je 4. Obsah trojuholníka DEF je rovný \frac12 \cdot 3 \cdot 4 = 6.
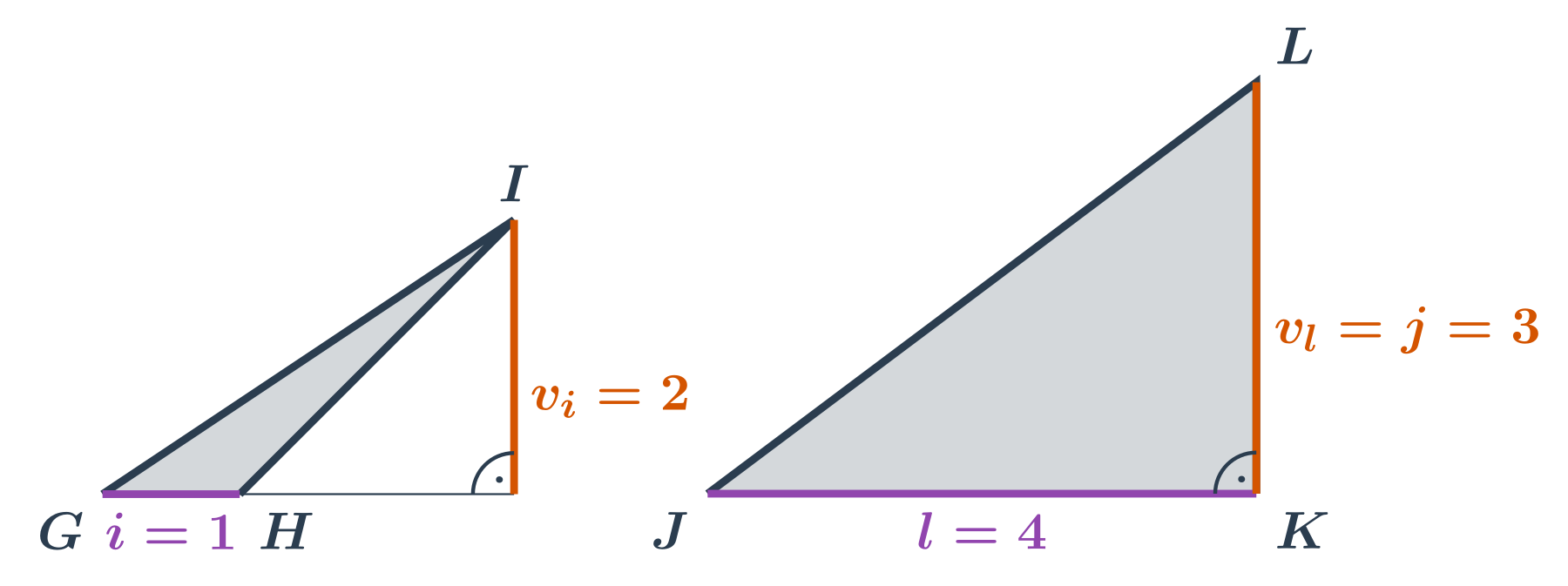
- Trojuholník GHI: Nevadí nám ani keď je päta kolmice, na ktorej leží výška, mimo stranu trojuholníka. Dĺžka strany \left| GH \right| je 1. Veľkosť k nej príslušnej výšky v_i je 2. Obsah trojuholníka GHI je \frac12 \cdot 2 \cdot 1 = 1.
- Trojuholník JKL: S pravouhlým trojuholníkom si tiež poradíme. Dĺžka strany \left| JK \right| je 4. Veľkosť k nej príslušnej výšky v_l je 3 (a je to zároveň aj dĺžka strany KL nášho trojuholníka). Obsah trojuholníka JKL je \frac12 \cdot 4 \cdot 3 = 6.
Obsah štvorca a obdĺžnika
Obsah štvorca so stranou dĺžky a je S=a\cdot a=a^2.
Obsah obdĺžnika so stranami s dĺžkami a,b je rovný S=a\cdot b.
HoreObsah rovnobežníka
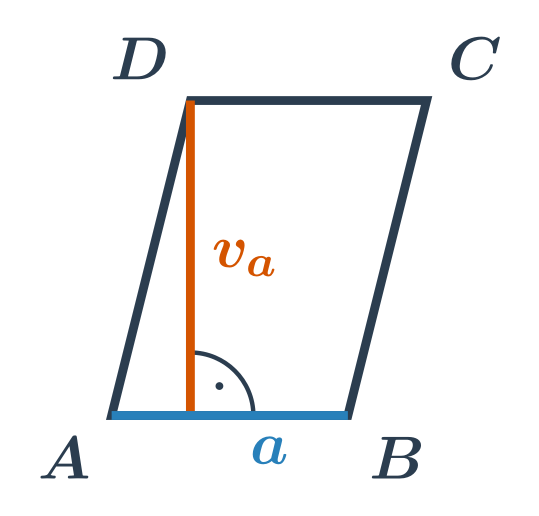
Obsah rovnobežníka, v ktorom k strane s dĺžkou a patrí výška v_a, vypočítame ako S= a\cdot v_a.
Obsah lichobežníka
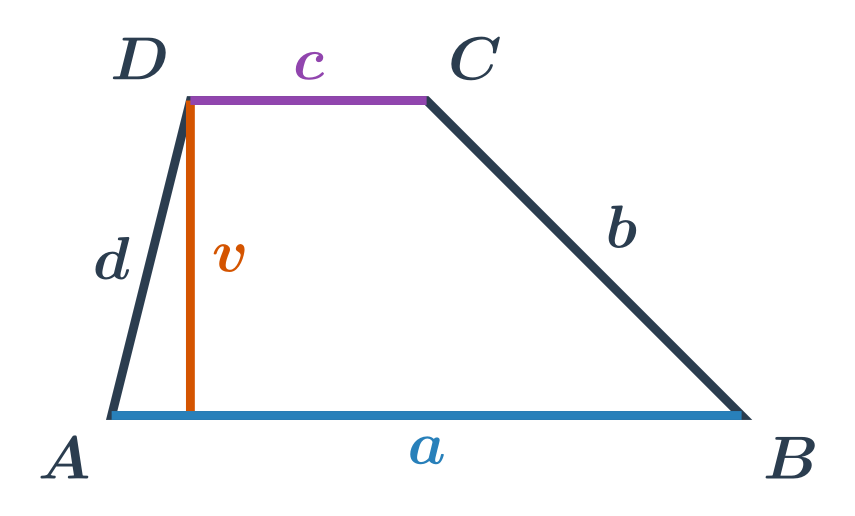
Obsah lichobežníka so základňami s dĺžkami a,c a výškou v vypočítame podľa vzorčeka S=\frac{1}{2} \cdot (a+c) \cdot v.
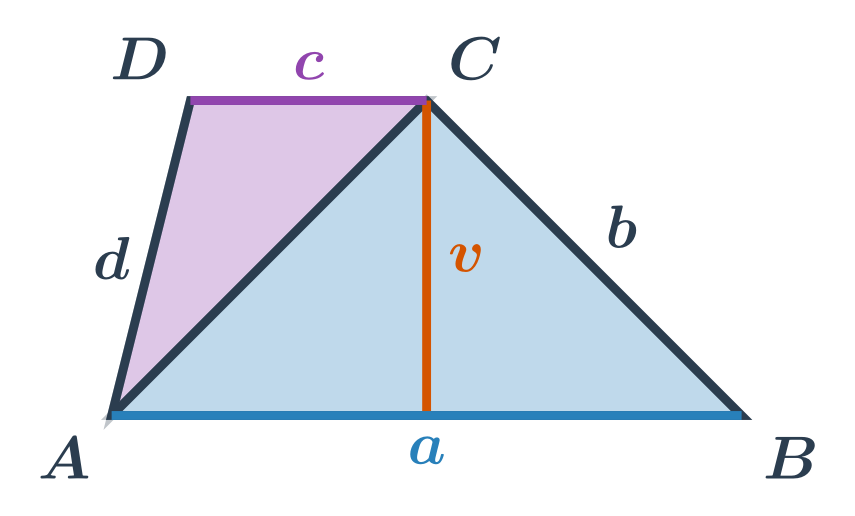
Intuíciu za týmto vzorčekom je vidieť na nasledujúcom obrázku. Obsah lichobežníka je rovný súčtu obsahov dvoch trojuholníkov.
- Prvý trojuholník má výšku v príslušnú k strane dĺžky a. Jeho obsah je S_{ABC}=\frac{1}{2} \cdot a \cdot v.
- Druhý trojuholník má výšku v príslušnú k strane dĺžky c. Jeho obsah je S_{ACD}=\frac{1}{2} \cdot c \cdot v.
Súčet obsahov týchto dvoch trojuholníkov je S = S_{ABC} + S_{ACD} = \frac{1}{2} \cdot a \cdot v + \frac{1}{2} \cdot c \cdot v = \frac{1}{2} \cdot (a+c) \cdot v
Obsah kruhu
Vzorce
Obvod kruhu (aj kružnice) s polomerom r je o=2\pi r. Pre priemer d platí o = \pi d.
Obsah kruhu s polomerom r je S=\pi r^2. Pre priemer d platí S = \frac{1}{4} \pi d^2.
Konštanta \pi sa nazýva tiež Ludolfovo číslo. \pi je iracionálne číslo, čo znamená, že ho nie je možné vyjadriť zlomkom ani zapísať presne v desiatkovej sústave. Približná hodnota \pi je 3,141 592 65.
Pri výpočte obsahu a obvodu kruhu dávame dobrý pozor na to, či vychádzame zo znalosti polomeru alebo priemeru. Zámena priemeru za polomer je častou chybou.
Intuícia
Základnú intuíciu za vzorcami na výpočet obsahu a obvodu kruhu približuje nižšie uvedený obrázok. Žlté štvorce majú obsah r^2. Oranžový štvorec sa skladá zo štyroch žltých štvorcov, takže má obsah 4\cdot r^2. Kruh má „o trochu menší“ obsah než oranžový štvorec, čo zodpovedá tomu, že obsah kruhu je približne 3{,}14 \cdot r^2. Obvod oranžového štvorca je 8\cdot r. Obvod kruhu je zase „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Príklady
- Majme kruh s polomerom 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm. Jeho obsah je \pi \cdot 3^2 \approx 3{,}14\cdot 9 \approx 28,3 cm².
- Kružnica s priemerom 2 cm má obvod \pi \cdot 2 \approx 6,3 cm. Jej vnútro má obsah \frac{1}{4} \pi \cdot 2^2 = \pi \approx 3,14 cm².
- Stredový kruh na futbalovom ihrisku má polomer 9{,}1 metru. Ak ho chceme obísť po jeho okrajovej čiare, prejdeme 2 \pi \cdot 9{,}1 \approx 57 metrov. Ak by sme chceli všetku trávu v kruhu nafarbiť na ružovo, museli by sme nafarbiť \pi \cdot 9{,}1^2 \approx 260 m² trávy.
Obsah kruhového výseku
Obsah kruhového výseku
Obsah kruhového výseku so stredovým uhlom \alpha a polomerom r vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2
Dĺžka oblúka
Podobne, dĺžku oblúka, ktorý na kružnici s polomerom r a zodpovedá stredovému uhlu \alpha vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Príklady
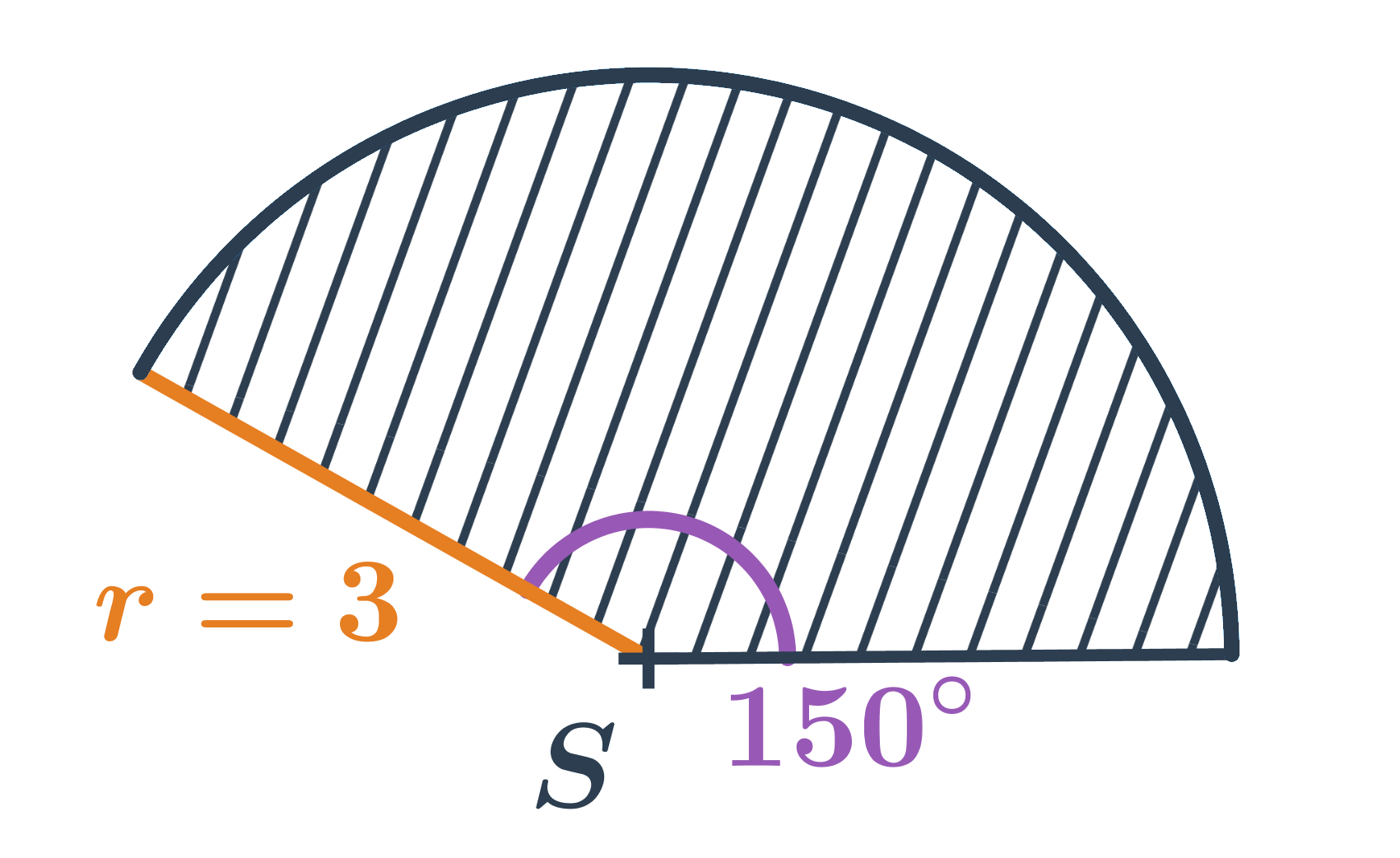
- Kruhový výsek na obrázku má obsah: \frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi
- Obsah celého kruhu (výseku so stredovým uhlom 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2
- Dĺžka oblúka na obrázku je: \frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
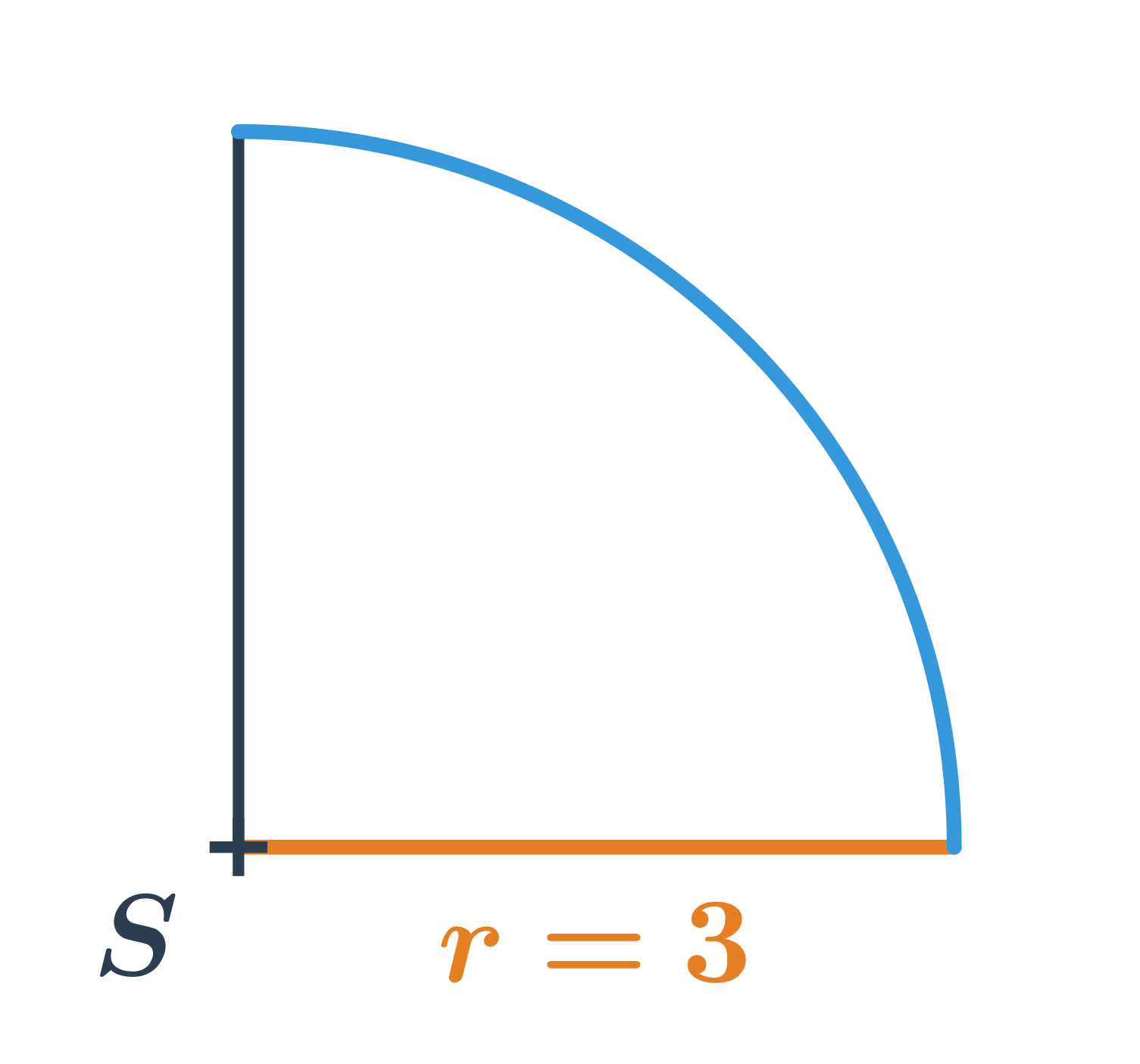
- Dĺžka celej kružnice (teda pre celých 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r
Obsah: mix
| Útvar | Vlastnosti | Obsah |
|---|---|---|
| trojuholník | strana a, príslušná výška v_a | S = \frac12 \cdot a\cdot v_a |
| štvorec | strana a | S = a^2 |
| obdĺžnik | strany a, b | S = a\cdot b |
| rovnobežník | strana a, príslušná výška v_a | S = a\cdot v_a |
| lichobežník | základne a, c, výška v | S = \frac12 \cdot (a+c) \cdot v |