Výpis prehľadov
Popisná štatistika
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Priemer a medián
Priemer a medián sú miery centrálnej (strednej) tendencie, vyjadrujú teda „typickú“ hodnotu premenných z určitej vzorky.
Priemer je súčet hodnôt vydelený ich počtom. Presnejšie povedané ide o aritmetický priemer (existujú aj iné druhy priemerov, napr. harmonický či geometrický).
Medián je stredná hodnota zo zoradenej postupnosti hodnôt. Je definovaný ako hodnota väčšia alebo rovná polovici hodnôt v súbore a menšia alebo rovná polovici hodnôt v súbore.
Príklad: Zoberme si súbor hodnôt 10, 3, 8, 4, 5. Priemer je súčet delený počtom, teda 30:5=6. Na určenie mediánu hodnoty najskôr zoradíme: 3, 4, 5, 8, 10. Medián je stredná hodnota, teda 5.
Ak má súbor párny počet prvkov, väčšinou sa za medián označuje priemer dvoch stredných hodnôt. Napríklad pre súbor hodnôt 10, 2, 9, 4, 14, 5 je zoradená postupnosť 2, 4, 5, 9, 10, 14. Hodnoty uprostred postupnosti sú 5 a 9, medián je teda 7.
Niekedy máme súbor hodnôt, ktoré je možné usporiadať podľa veľkosti, ale nie je možné vypočítať aritmetický priemer dvoch hodnôt. Napríklad pre súbor štyroch hodnôt S, M, XL, XXL veľkostí oblečenia spĺňa definíciu mediánu akákoľvek hodnota od M do XL, teda M, L, i XL.
HoreKvantily a kvartily
Kvantily sú charakteristiky polohy štatistického znaku podobne ako napr. aritmetický priemer a medián. Kvantily je možné určiť pre ordinálne, intervalové a pomerné typy dát.
Súbor n hodnôt usporiadame podľa veľkosti: x_1 \le x_2 \le \ldots \le x_{n-1} \le x_n
Majme číslo \theta medzi nulou a jednotkou. Kvantil Q_{\theta} je hodnota, ktorá delí usporiadanú postupnosť hodnôt v súbore na dolnú a hornú časť tak, že dolná časť obsahuje aspoň \theta \cdot n hodnôt a horná časť aspoň (1-\theta)\cdot n hodnôt.
x_1 \le \ldots \le x_c \le Q_{\theta} \le x_{c+1} \le \ldots \le x_n
- Ak je \theta \cdot n necelé číslo, a najbližšie väčšie celé číslo je k, väčšinou zvolíme Q_{\theta}=x_k.
- Ak je \theta \cdot n=m celé číslo, zvolíme Q_{\theta} = \frac{x_{m}+x_{m+1}}{2} (keď je možné tento aritmetický priemer spočítať — teda pre intervalové a pomerové znaky).
Napríklad vezmeme súbor ôsmich čísel 0,0,0,0,1,2,3,4. Kvantil Q_{0{,}1} určíme takto: 0{,}1 \cdot 8 = 0{,}8, najbližšie väčšie celé číslo je 1, takže Q_{0{,}1}=x_1=0. Kvantil Q_{0{,}75} určíme takto: 0{,}75 \cdot 8 = 6, takže Q_{0{,}75}=\frac{x_6+x_7}{2}=\frac{2+3}{2}=2{,}5.
Pre ordinálne znaky nemusí byť možné vypočítať aritmetický priemer. Ako kvantil Q_{\theta} potom zvolíme niektorú hodnotu, ktorá vhodne delí usporiadanú postupnosť hodnôt súboru.
Napríklad spočítajme kvantil Q_{0{,}8} pre hodnoty S, S, M, L, XXL znaku „veľkosť oblečenia“. 5 \cdot 0{,}8=4, Q_{0{,}8} je akákoľvek hodnota medzi x_4 a x_5, teda L,XL, alebo XXL.
p% kvantil Q_{\frac{p}{100}} sa nazýva p. percentil.
Niektoré významné kvantily:
| kvantil | názov |
|---|---|
| Q_{0{,}5} | medián |
| Q_{0{,}25} | dolný kvartil |
| Q_{0{,}75} | horný kvartil |
| Q_{0{,}01},Q_{0{,}02},\ldots, Q_{0{,}99} | 1. percentil, 2. percentil, … , 99.percentil |
Medzikvartilové rozpätie je rozdiel horného a dolného kvartilu: Q_{0{,}75}-Q_{0{,}25} Medzikvartilové rozpätie (niekedy označované ako IQR) je možné vypočítať pro intervalové a pomerové znaky.
Napríklad, určime medzikvartilové rozpätie pre súbor hodnôt 0,0,0,0,1,2,3,4. Horný kvartil Q_{0{,}75} sme vypočítali už skôr, je to 2{,}5. Dolný kvartil Q_{0{,}25} je \frac{x_2+x_3}{2}=\frac{0+0}{2}=0. Medzikvartilové rozpätie je 2{,}5-0=2{,}5.
HoreAbsolútna a relatívna početnosť
Štatistický súbor má rozsah n, keď obsahuje presne n jednotiek. Napríklad štatistickým súborom s rozsahom 10 môže byť skupinka 10 detí z tretej triedy. Jednotliví žiaci a žiačky sú potom jednotkami štatistického súboru.
Príklady štatistických znakov, ktoré nás môžu zaujímať: meno, výška, známka z prvouky. Predpokladajme, že mená detí z našej skupinky desiatich žiakov a žiačok sú: Anna, Eva, Ján, Ján, Ján, Vanesa, Vanesa, Mirka, Tobiáš, Tomáš.
Znak meno teda v našom štatistickom súbore nadobúda siedmich rôznych hodnôt – Anna, Eva, Ján, Vanesa, Mirka, Tobiáš, Tomáš. Niektoré deti môžu mať rovnaké meno.
Absolútnou početnosťou hodnoty znaku v danom štatistickom súbore je počet jednotiek zo štatistického súboru, ktoré majú danú hodnotu znaku.
Napríklad absolútna početnosť hodnoty „Ján“ znaku meno je 3, pretože v skupinke sú traja žiaci s menom Ján. Absolútna početnosť hodnoty „Eva“ znaku meno je 1.
Relatívnu početnosť hodnoty znaku v danom štatistickom súbore vypočítame ako podiel počtu jednotiek s danou hodnotou znaku počtom všetkých jednotiek štatistického súboru. Tiež sa dá povedať, že relatívna početnosť hodnoty znaku je podiel absolútnej početnosti tejto hodnoty znaku a rozsahu n štatistického súboru. Relatívna početnosť sa zadáva ako číslo v intervale [0,1] alebo v percentách.
Napríklad relatívna početnosť hodnoty „Vanesa“ znaku meno je \frac{2}{10}=0{,}2, pretože v skupinke celkovo desiatich detí sú dve žiačky s menom Vanesa. Relatívnu početnosť hodnoty „Vanesa“ znaku meno môžeme zapísať tiež ako 20\ \%.
Súčet absolútnych početností všetkých hodnôt jedného znaku sa rovná rozsahu n daného štatistického súboru.
Súčet relatívnych početností všetkých hodnôt jedného znaku je 1 alebo tiež 100\ \%.
HoreKorelačný koeficient
Korelácia je vzťah medzi dvomi veličinami. Korelačný koeficient je číslo, ktoré vyjadruje silu tohto vzťahu.
Existuje viac spôsobov, ako koreláciu merať. Najčastejšie používaný je Pearsonov korelačný koeficient. Ten sa značí r a má nasledujúce vlastnosti:
- Nadobúda hodnôt z intervalu [-1, 1].
- Meria len lineárnu závislosť medzi veličinami.
- Ak je hodnota kladná, zodpovedá zväčšenie jednej veličiny zväčšeniu druhej.
- Ak je hodnota záporná, zodpovedá zväčšenie jednej veličiny zmenšeniu druhej.
- Ak je hodnota nulová, nie je medzi veličinami lineárna závislosť.
- Ak je hodnota presne 1 alebo -1, je medzi veličinami presná lineárna závislosť.
Typy štatistických dát
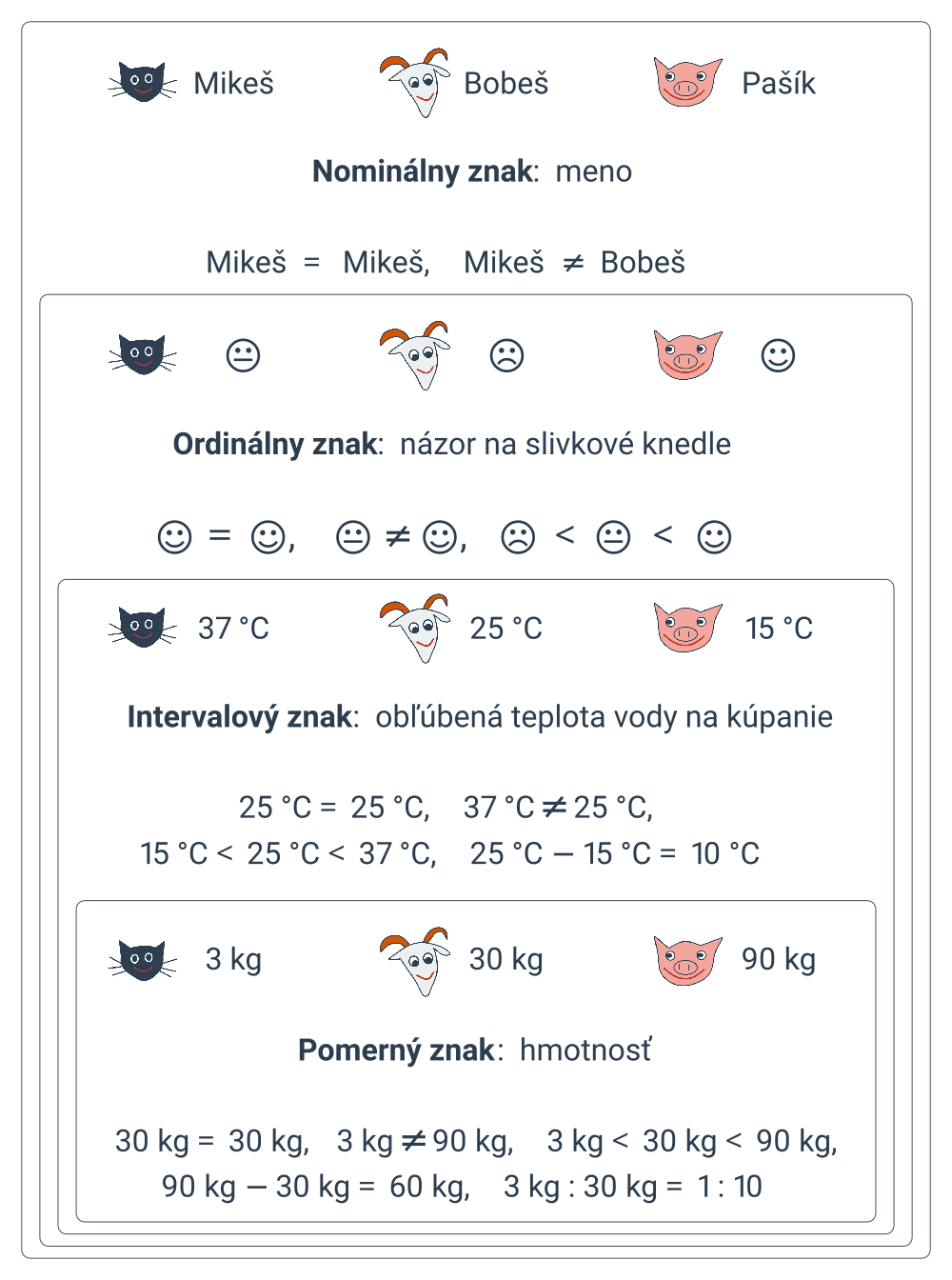
Zamyslime sa nad štatistickým súborom zvieratiek z Hrusíc. Vezmime z neho tri jednotky na ukážku: kocúrika Mikeša, kozla Bobeša a prasiatko Pašíka. Budeme si pri nich všímať rôzne typy znakov.
Nominálny znak nadobúda hodnôt, pri ktorých môžeme testovať rovnosť, teda určiť, či sú rovnaké alebo rôzne. Napríklad meno, farba.
Ordinálny znak nadobúda hodnôt, pri ktorých môžeme testovať rovnosť a ktoré ešte aj dokážeme porovnávať, teda určiť, ktorá z dvoch rôznych hodnôt je menšia a ktorá väčšia. Napríklad známka z matematiky, veľkosť oblečenia (XS, S, M, L, XL), obľuba brokolicovej polievky („fuj“,„dá sa“,„mňam“).
Intervalový znak nadobúda hodnôt, pri ktorých môžeme testovať rovnosť, porovnávať ich a určiť rozdiel dvoch hodnôt, teda rovnaký interval medzi jednou a druhou dvojicou hodnôt vyjadruje aj rovnaký rozdiel v intenzite skúmanej vlastnosti. Napríklad teplota v stupňoch Celzia, rok narodenia.
Pomerný znak nadobúda hodnôt, pri ktorých môžeme testovať rovnosť, porovnávať ich, určiť rozdiel dvoch hodnôt a určiť pomer dvoch hodnôt, teda spočítať ich podiel, ktorý zmysluplne vyjadruje koľkokrát je jedna hodnota väčšia než druhá. Napríklad teplota v stupňoch Kelvina, hmotnosť. Teplota v stupňoch Celzia môže ísť aj do záporných čísel a teleso s teplotou 10 °C nemá dvakrát väčšiu kinetickú energiu častíc než teleso s teplotou 5 °C, takže teplota v stupňoch Celzia nie je pomerný znak.
Alternatívny znak je pojem mimo túto hierarchiu, znamená to, že znak nadobúda len dve hodnoty. Napríklad zdravý – chorý, s topánkami – bez topánok.
Priemer, medián a modus (použitie)
Aritmetický priemer, medián a modus sú charakteristiky polohy znaku. Používame ich k popisu typickej hodnoty znaku.
Aritmetický priemer pre daný súbor sa počíta ako podiel súčtu hodnôt znaku rozsahom súboru.
- Aritmetický priemer je možné vypočítať pre intervalové a pomerové znaky.
- Najlepšie sa hodí k popisu typickej hodnoty znaku, ktorý nadobúda v danom súbore podobných hodnôt bez príliš odlišných extrémov, ktoré by aritmetický priemer vychýlili mimo typické hodnoty.
Príklad použitia aritmetického priemeru – súbor hodnôt 122, 116, 120, 118 znaku „výška dieťaťa v cm“ má aritmetický priemer 119.
Medián delí rad vzostupne zoradených hodnôt na dve rovnako početné polovice.
- Pre nepárny počet hodnôt je medián stredný prvok.
- Pre párny počet hodnôt môže definícii mediánu zodpovedať viac hodnôt, niekedy sa v takom prípade berie ako medián aritmetický priemer dvoch prostredných hodnôt (samozrejme len ak pre daný znak aritmetický priemer môžeme vypočítať).
- Medián je možné určiť pre ordinálne, intervalové a pomerové znaky.
- Nie je ovplyvnený extrémnymi hodnotami ako aritmetický priemer.
Príklad použitia mediánu – súbor hodnôt 1, 1000, 1002, 1003 znaku „hmotnosť krokodíla v kg“ má medián 1001 (alebo akékoľvek číslo od 1000 do 1002). Extrémne malá hodnota 1 spôsobí, že aritmetický priemer je 751{,}5, čo nezodpovedá typickej hodnote „niečo málo cez 1000 kg“.
Modus je hodnota znaku, ktorá má v danom súbore najväčšiu relatívnu (i absolútnu) početnosť.
- Takých hodnôt môže byť viac než jedna.
- Modus môžeme vypočítať pre nominálne, ordinálne, intervalové a pomerové znaky.
Príklad použitia – modus súboru hodnôt 1, 1, 1, 1, 2, 2 znaku „počet hrbov ťavy“ je 1.
Hore
