Priestorové útvary

Priestorové útvary sú množiny bodov v priestore, ide teda o trojrozmerné útvary. Najznámejšie priestorové útvary sú napríklad kocka, kváder, ihlan, guľa, hranol, valec, kužeľ.

Pri niektorých priestorových útvaroch dokážeme jednoducho vypočítať ich objem a povrch.

Kocka a kváder sú priestorové geometrické útvary, ktoré patria medzi mnohosteny, špeciálnejšie ide o zvláštne prípady hranolov.

Kocka je priestorový útvar, ktorý má šesť stien, tvar každej steny je štvorec. Všetky hrany kocky majú rovnakú dĺžku a všetky vnútorné uhly sú pravé, teda ich veľkosť je 90°. Príklady kocky v bežnom živote zahŕňajú kocky cukru alebo Rubikovu kocku.

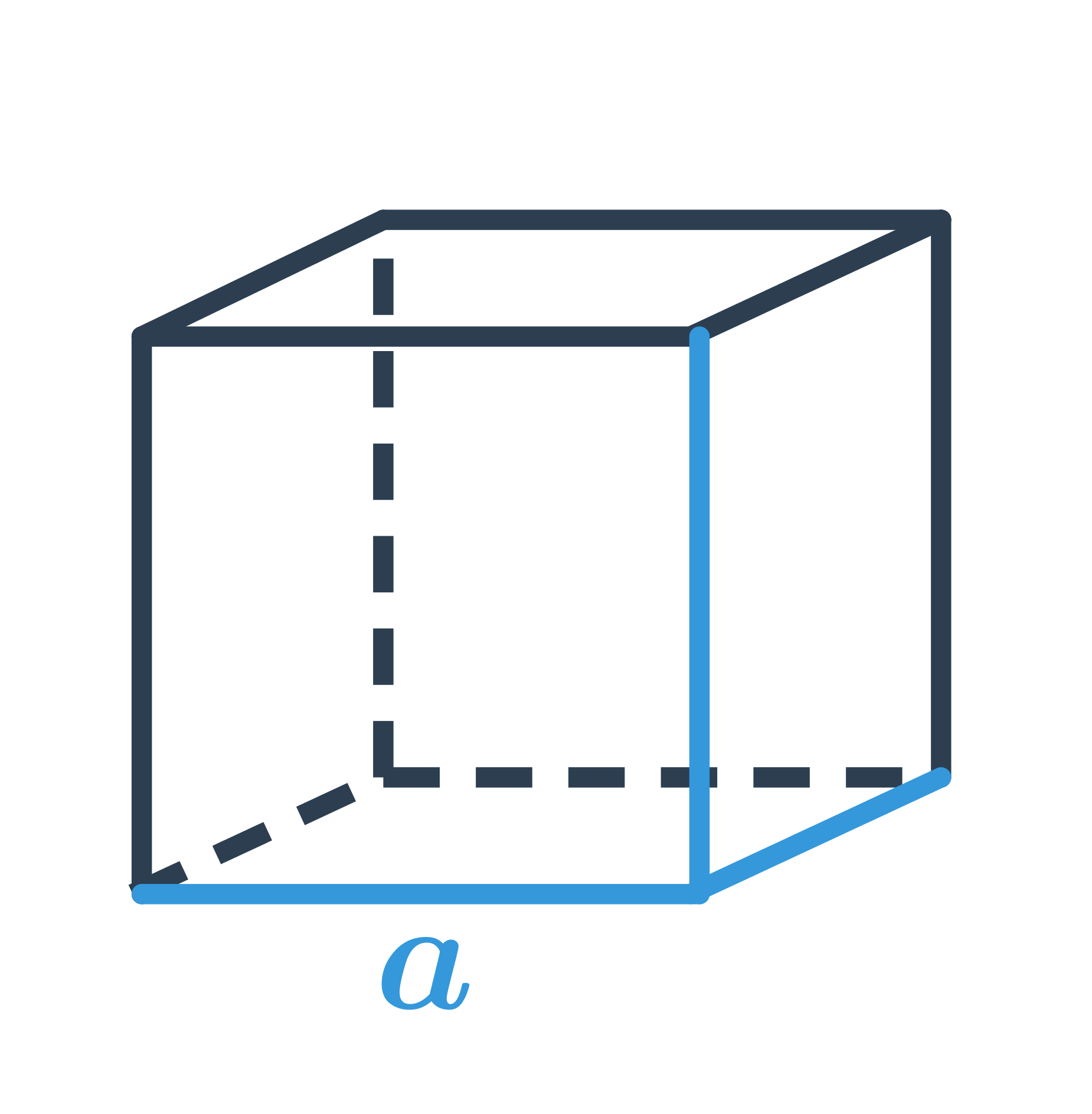
Na výpočet objemu kocky použijeme vzorec V = a^3, kde a je dĺžka hrany kocky.

Povrch kocky s dĺžkou hrany a sa vypočíta pomocou vzorca S = 6a^2.

Kváder je tiež hranol, ale na rozdiel od kocky majú jeho steny tvar obdĺžnikov. Kváder má tri rozmery: šírku, dĺžku a výšku, ktoré nemusia byť rovnaké, ako je tomu v prípade kocky. Kváder má šesť stien, tvar každej steny je obdĺžnik alebo štvorec, ak sú všetky steny tvaru štvorca, ide o kocku.

Príklady kvádrov v bežnom živote zahŕňajú krabice, knihy alebo tehly.

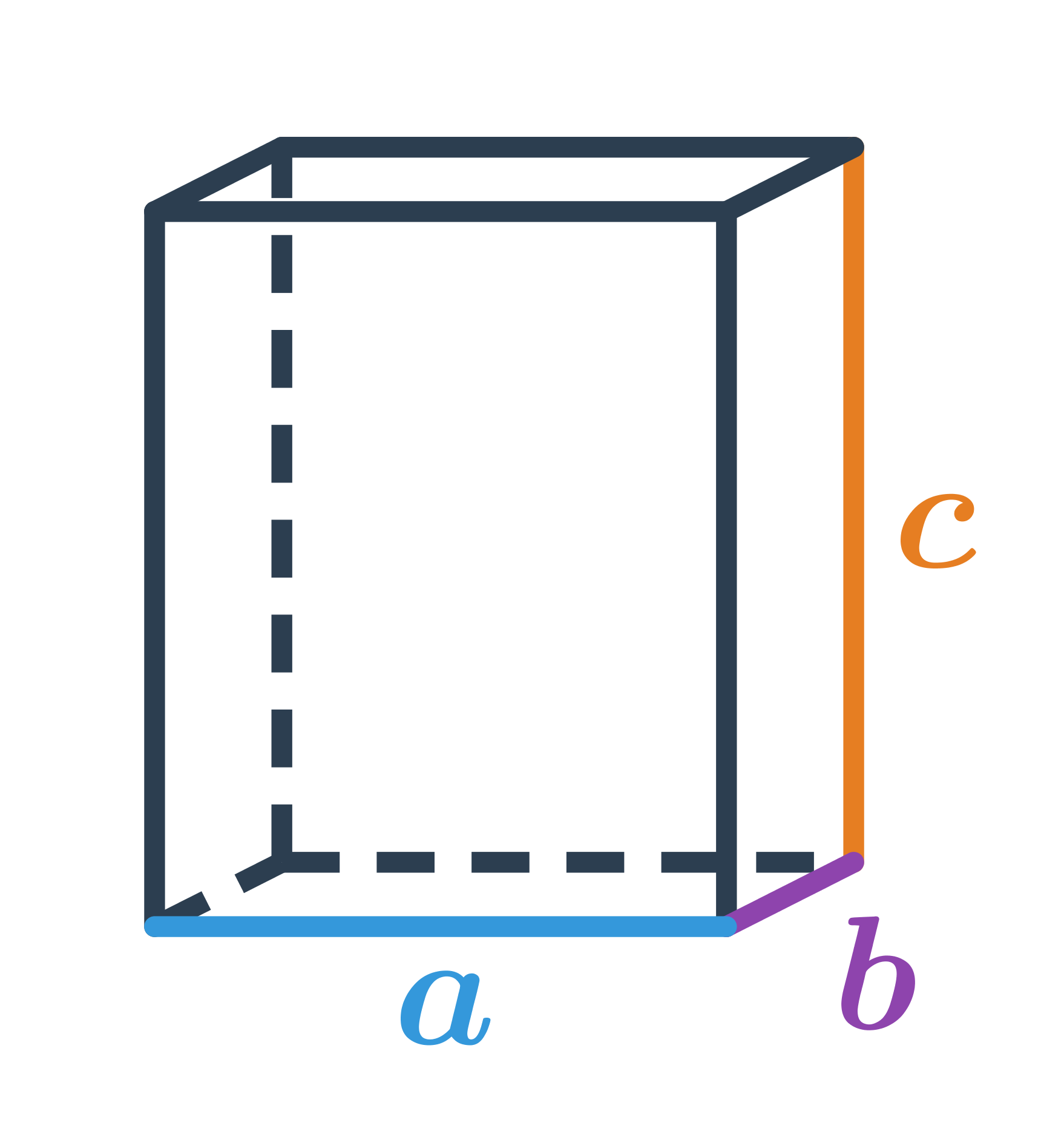
Objem kvádra získame vzorcom V = a \cdot b \cdot c, kde a,b,c sú rozmery kvádra.

Povrch kvádra vypočítame ako súčet obsahov všetkých jeho šiestich obdĺžnikových stien S = 2(ab + bc + ac). Dvojice protiľahlých stien sú zhodné obdĺžniky, preto majú rovnaké obsahy.

Hranol je priestorový geometrický útvar, ktorý má dve zhodné podstavy umiestnené v rôznych rovinách. Budeme sa zaoberať kolmými hranolmi, v ktorých sú zodpovedajúce strany podstavy vždy spojené bočnou stenou tvaru obdĺžnika alebo štvorca. (Pre kosé hranoly sú bočné steny rovnobežníky.) Podstavy hranola môžu mať rozličné tvary, napríklad môžu byť trojuholníkové, štvorcové, obdĺžnikové alebo aj mnohouholníkové.

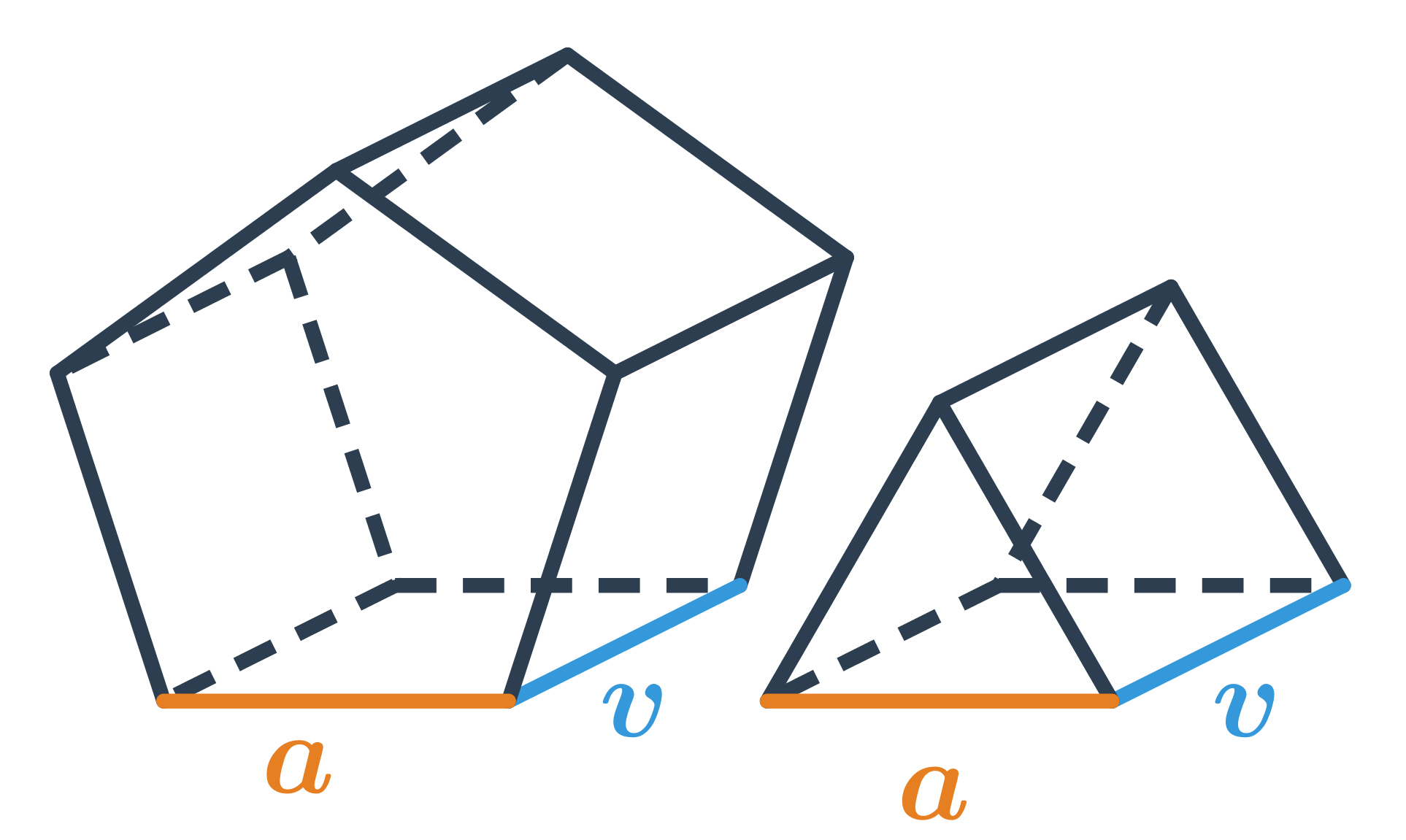
Vzorčeky pre objem a povrch hranola

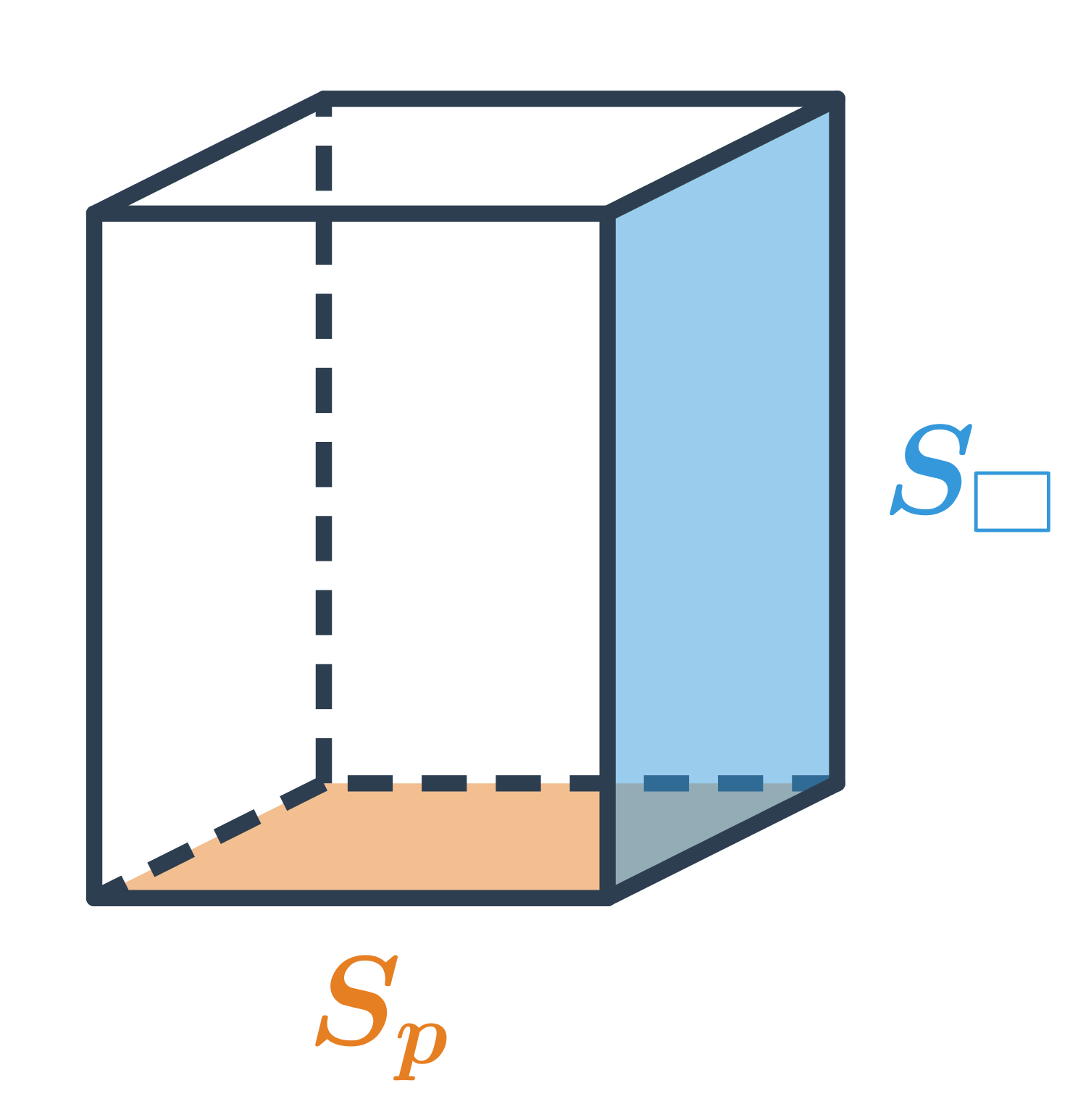
Pre výpočet objemu hranola používame vzorec V = S_p \cdot v, kde S_p je obsah jednej podstavy a v je výška hranola.

Sieť hranola sa skladá z dvoch podstáv a plášťa, preto jeho povrch vypočítame ako súčet obsahov podstáv a obsahu plášťa: S = 2S_p + S_{pl}, kde S_{pl} je obsah plášťa, čo je súčet obsahov všetkých obdĺžnikových alebo štvorcových stien tvoriacich plášť.

Príklady hranolov

Pravidelný n-boký hranol má ako podstavy dva pravidelné n-uholníky.

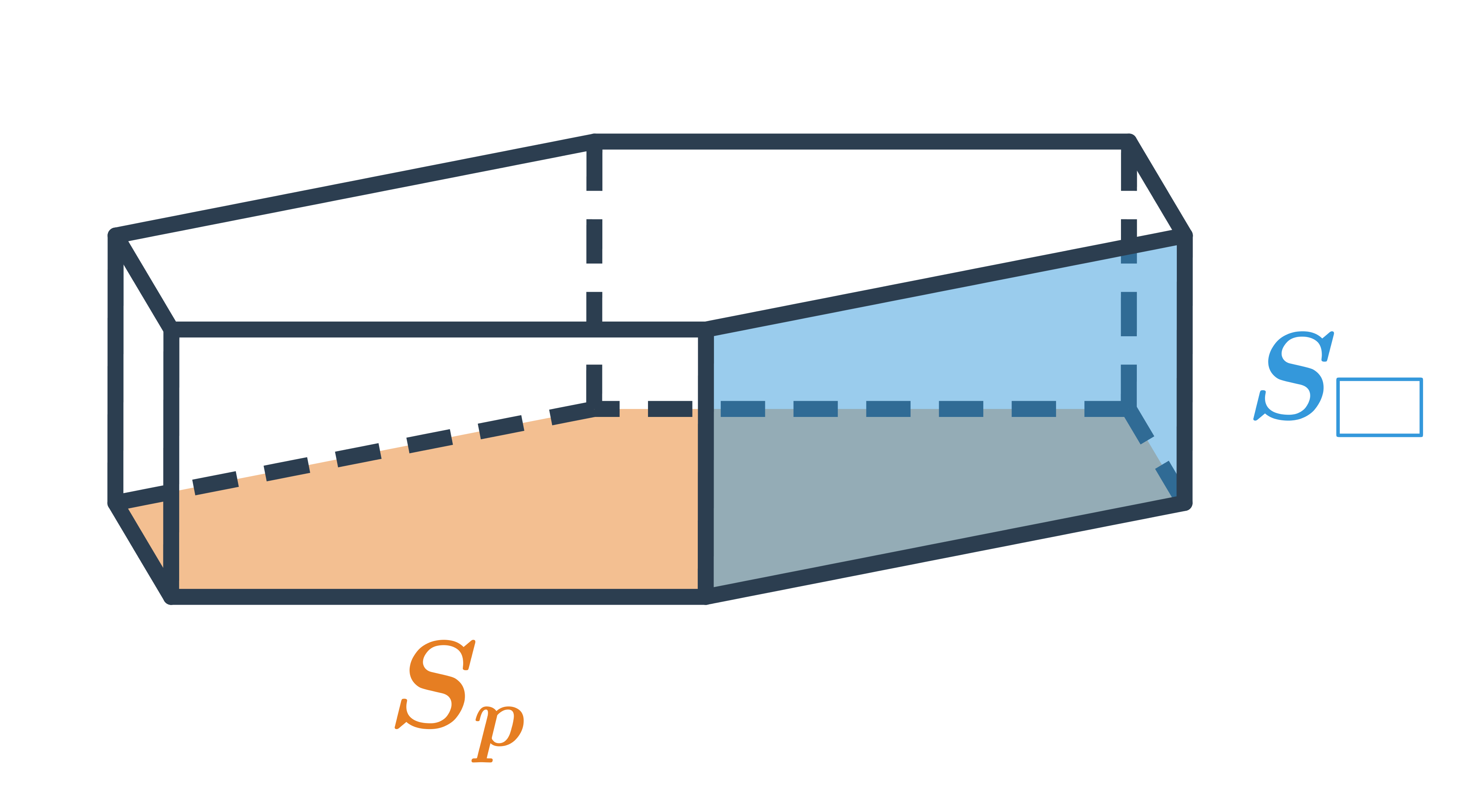
Špeciálne prípady štvorbokých hranolov sú kváder a kocka. Kváder môže a nemusí byť pravidelný štvorboký hranol. Kocka je pravidelný štvorboký hranol, ktorý navyše spĺňa a=v.

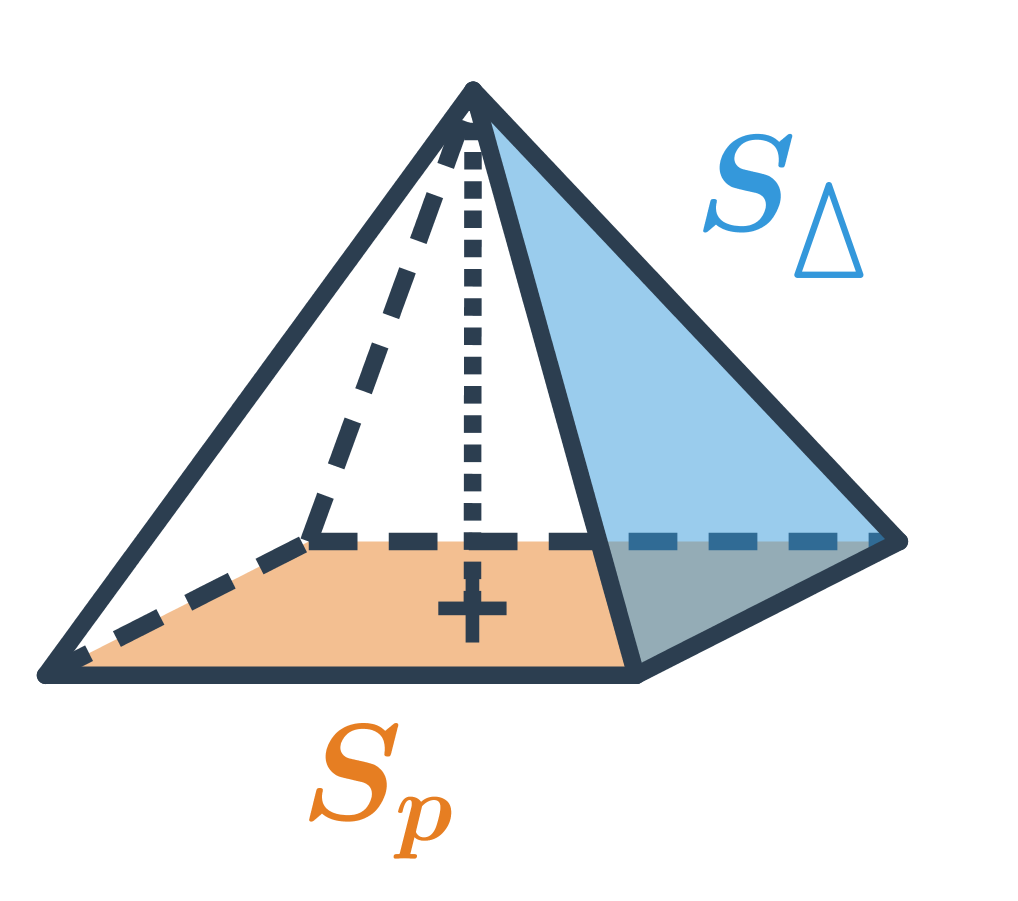
Ihlan je priestorový geometrický útvar, ktorý má jednu podstavu a plášť tvorený trojuholníkmi. Podstava ihlanu môže byť ľubovoľný mnohouholník (napríklad štvorec, obdĺžnik alebo trojuholník) a všetky bočné steny (plášť) sa stretávajú v jednom spoločnom bode nazývanom vrchol ihlanu. Príkladom ihlanov sú pyramídy zo starovekého Egypta, vypadajú zhruba ako ihlany so štvorcovou podstavou a štyrmi trojuholníkovými bočnými stenami.

Vzorce pre objem a povrch

Objem ihlanu V = \frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy a v je výška ihlanu, čo je vzdialenosť vrcholu od roviny podstavy. (Veľkosť výšky ihlanu získame ako dĺžku úsečky, ktorá vedie od vrcholu k rovine podstavy a je kolmá na túto rovinu.)

Povrch ihlanu získame ako súčet obsahu podstavy a obsahu plášťa S_p (obsah plášťa je rovný súčtu obsahov všetkých bočných trojuholníkových stien ihlanu). Celkovo je povrch ihlanu S = S_p + S_{pl}, v prípade pravidelného šesťbokého ihlanu na obrázku je: S=Sp + 6 \cdot S_{\Delta}

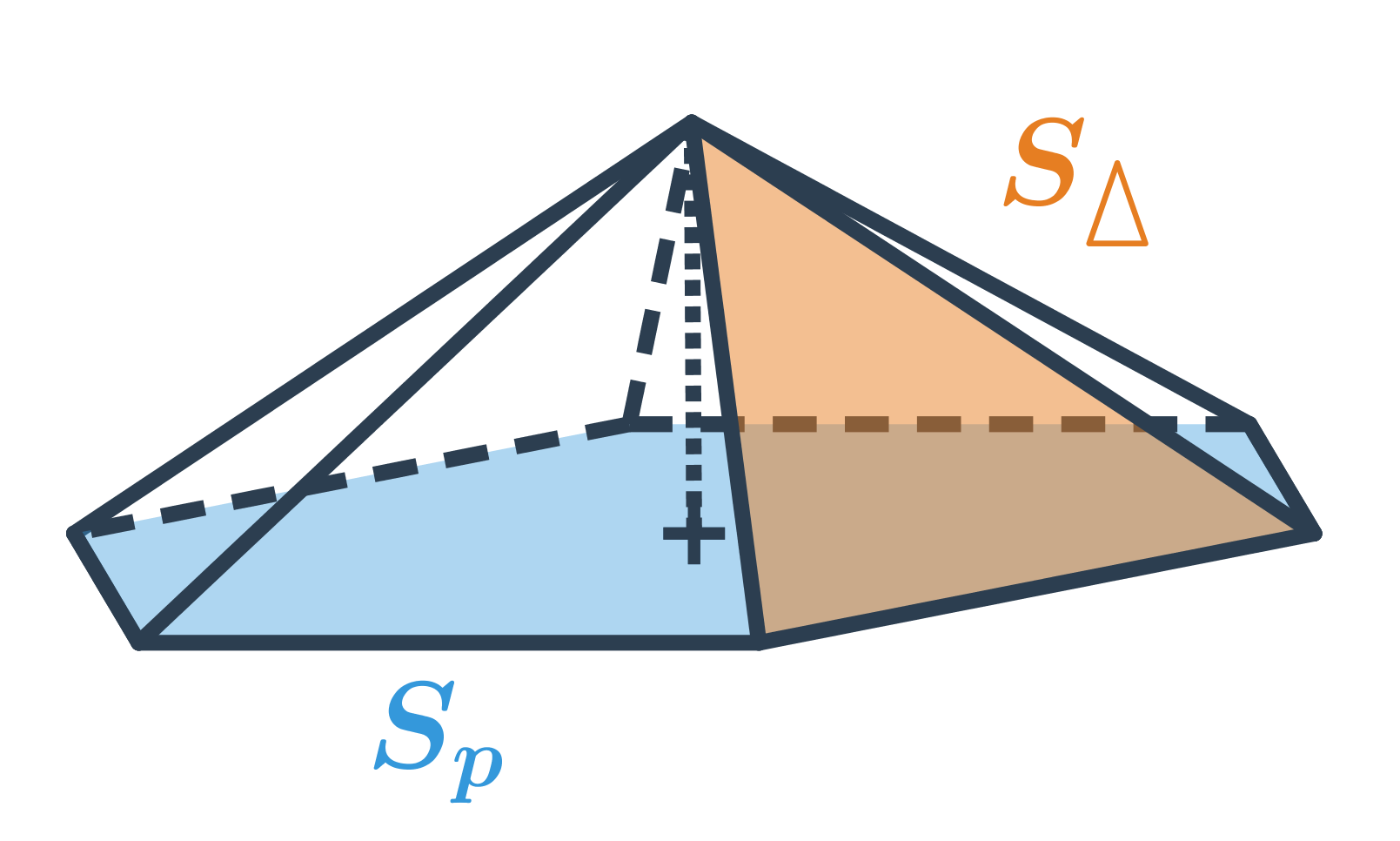
Niektoré ihlany majú pravidelnú podstavu, vrchol umiestnený priamo nad stredom podstavy a všetky trojuholníkové steny z plášťa rovnaké, ale všeobecne sa môže výpočet obsahu každej z týchto trojuholníkových stien líšiť v závislosti od tvaru podstavy ihlanu.

Špeciálne prípady

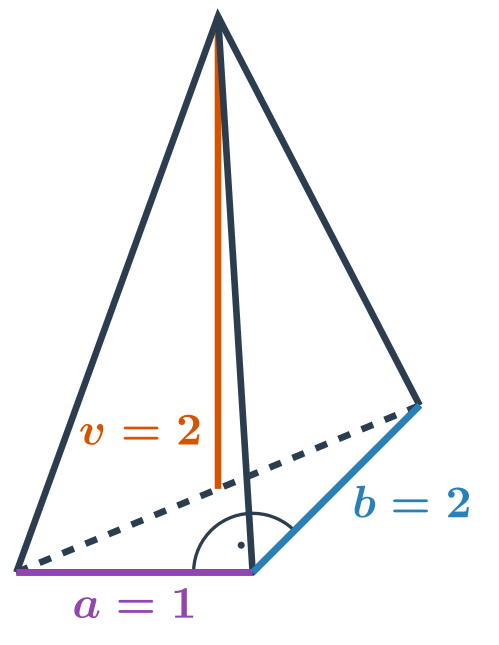
Pravidelný štvorsten je ihlan, ktorého základňa aj všetky tri bočné steny sú rovnostranné trojuholníky. Je jedným z Platónskych telies.

Ak máme pravidelný štvorsten, ktorého steny sú rovnostranné trojuholníky s dĺžkou každej strany a, vieme si pomocou Pytagorovej vety vypočítať výšku každého z týchto rovnostranných trojuholníkov \frac{\sqrt{3}}{2} a.

Pravidelný n-boký ihlan má ako podstavu pravidelný n-uholník, jeho plášť tvorí n rovnoramenných trojuholníkov. Napríklad podstava pravidelného štvorbokého ihlanu je štvorec, jeho plášť tvoria štyri rovnoramenné trojuholníky.

Valec je teleso, ktoré vznikne rotáciou obdĺžnika v priestore okolo jednej strany.

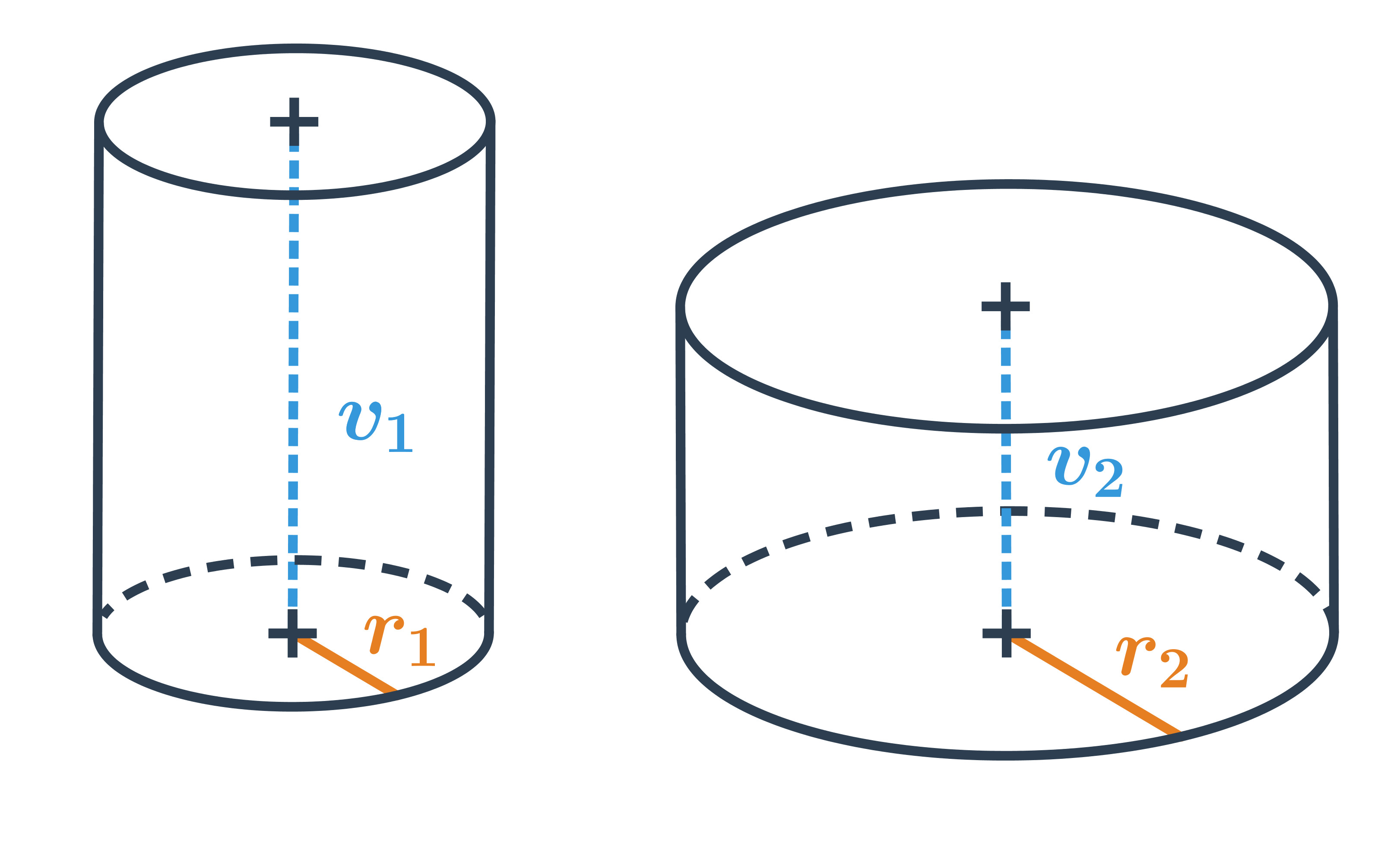
Valec má dve podstavy tvaru kruhu, je jednoznačne určený polomerom (alebo priemerom) podstavy a výškou.

Vzorce na výpočet objemu a povrchu valca

Objem valca vypočítame podobne ako pri hranole V=S_p \cdot v, kde S_p je obsah kruhovej podstavy. Celkovo je teda objem valca: V=\pi \cdot r^2 \cdot v

Povrch valca je súčet obsahov jeho dvoch podstáv a obsahu plášťa S = 2\cdot S_p + S_{pl}. Podstavy sú v tvare kruhu a plášť môžeme rozvinúť do roviny ako obdĺžnik s rozmermi v a 2\pi \cdot r (výška valca a obvod jeho podstavy). Povrch valca je rovný: V = 2\pi \cdot r^2 + 2\pi \cdot r \cdot v = 2\pi r (r+v)

Guľa je priestorový geometrický útvar, ktorý má tvar dokonale guľatého telesa. Všetky body na povrchu gule sú rovnako ďaleko od stredu, táto vzdialenosť sa nazýva polomer gule. Guľa je symetrická vo všetkých smeroch, čo znamená, že nezáleží na tom, ako ju otočíme, jej tvar zostane rovnaký.

Príklady gule v bežnom živote zahŕňajú basketbalovú loptu, zemeguľu alebo guľôčku z ložiska.

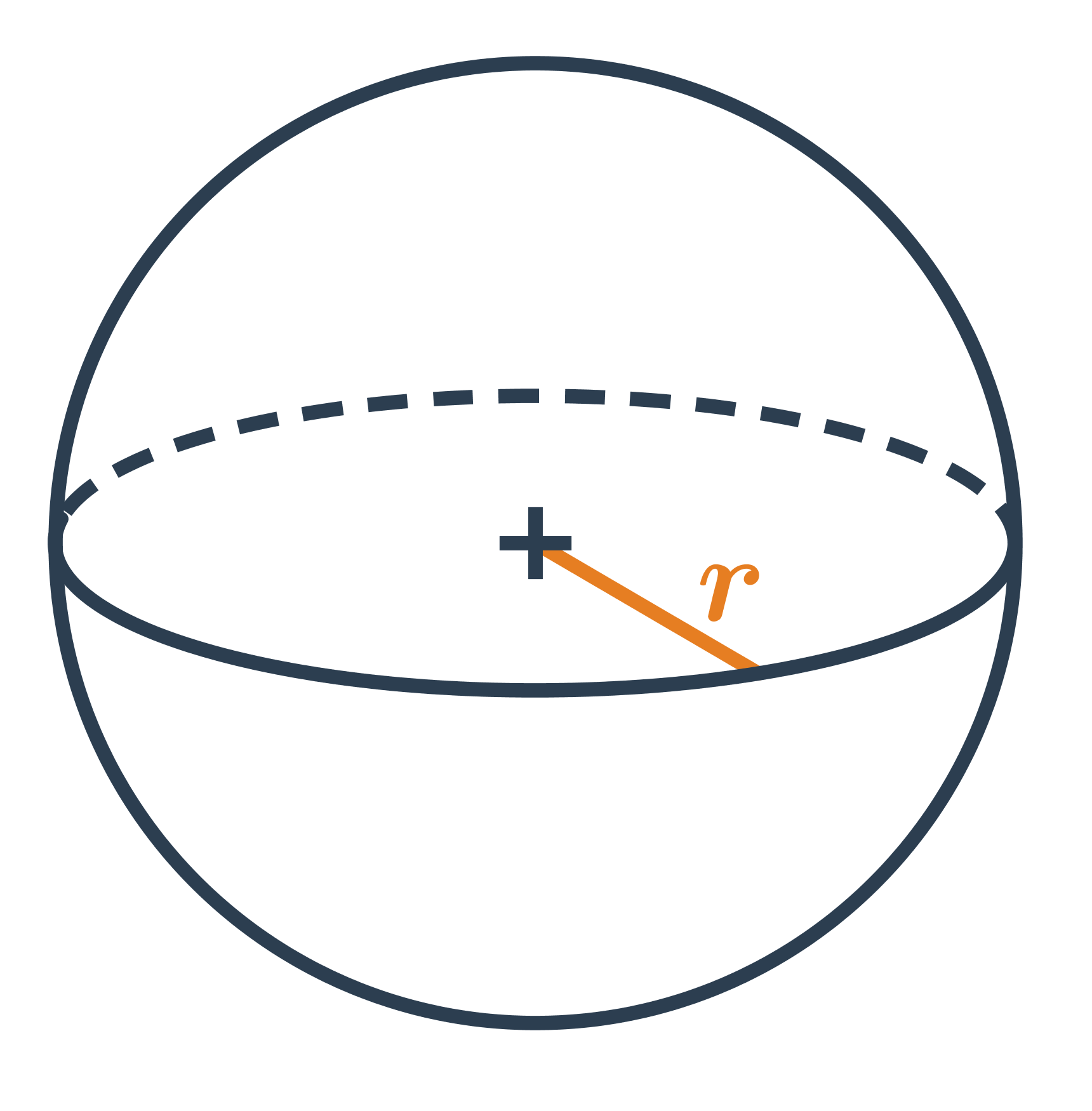
Na výpočet objemu gule používame vzorec V = \frac{4}{3} \pi r^3, kde r je polomer gule.

Povrch gule sa vypočíta pomocou vzorca S = 4 \pi r^2, kde zase r značí polomer gule.

Guľa nemá rohy ani hrany, čo ju odlišuje od mnohých iných geometrických útvarov. Táto jedinečná vlastnosť dáva guli významnú rolu v rôznych oblastiach, vrátane fyziky, kde sa používa napríklad na modelovanie ideálnych telies v teórii gravitácie. 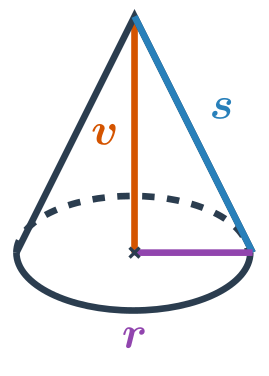Predmetom štúdia v neeuklidovskej geometrii môžu zase byť útvary, ktoré nie sú časťou roviny, ale guľovej plochy (potom ide o sférickú geometriu, teda geometriu na sfére).

Kužeľ je priestorový geometrický útvar s kruhovou podstavou. Zužuje sa smerom k jednému bodu zvanému vrchol. Ide o útvar, ktorý vznikne, keď sa okolo svojej osi otáča rovnoramenný trojuholník. Príkladom kužeľa v bežnom živote je kornút zmrzliny alebo dopravný kužeľ. 

Vzorce pre objem a povrch

Objem kužeľa je možné vypočítať pomocou vzorca: V = \frac{1}{3} \pi \cdot r^2 \cdot v, kde r je polomer podstavy a v je výška kužeľa, čo je vzdialenosť vrcholu od roviny, v ktorej leží podstava kužeľa.

Povrch kužeľa získame sčítaním obsahu základne a obsahu plášťa S = \pi \cdot r^2 + \pi \cdot r s, kde s je tzv. strana kužeľa, čo je dĺžka úsečky spájajúca vrchol kužeľa s okrajom jeho základne.

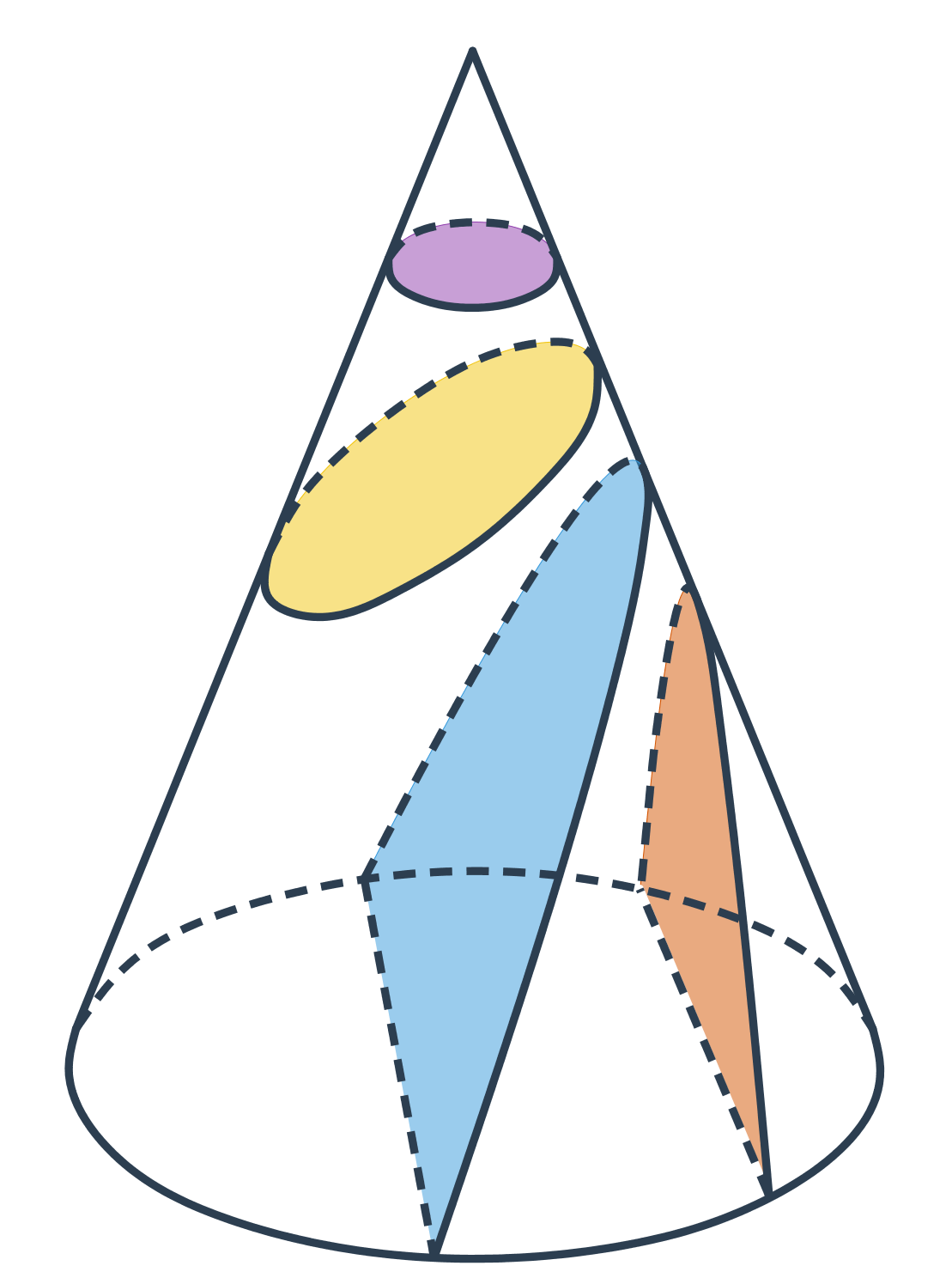
Kužeľosečky

Krivky, ktoré vznikajú prienikom kužeľového povrchu s rovinou sa nazývajú kužeľosečky. Patria medzi ne napríklad kružnica, elipsa, parabola a hyperbola.