Výpis prehľadov
Operácie s vektormi
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Operácie s vektormi
Vektory v rovine môžu byť zapísané ako dvojice čísel – súradníc v rovine, podobne trojrozmerné vektory je možné zapísať ako trojice čísel – súradníc v priestore.
Operácie ako súčet, rozdiel a vynásobenie reálnym číslom, ktoré vieme jednoducho vykonávať s číslami, je možné s vektormi vykonávať po jednotlivých súradniciach. Tým sa zaoberá kapitolka Vektory: násobenie konštantou, súčet, rozdiel. Príklady praktického použitia týchto operácií s vektormi:
- vrabec letí rovnakým smerom ako mucha a dvakrát rýchlejšie než mucha – vektor rýchlosti vrabca získame, keď vektor rýchlosti muchy vynásobíme konštantou 2,
- satelitné snímky ukazujú, že ráno ešte vozidlo Marka Watneyho stálo na marsovskej základni, za dnes prekonal 50 km na východ – jeho novú polohu získame, keď k súradniciam základne pripočítame vektor (50;0),
- slimák preliezol rovno po monitore z ľavého horného rohu (súradnice v pixeloch [0;0]) do bodu [1007;555] – vektor, ktorého súradnice sú počty pixelov, ktoré slimák prekonal v horizontálnom a vertikálnom smere, získame ako rozdiel jeho umiestnenia na konci pohybu a jeho umiestnenia na začiatku pohybu.
Špeciálna operácia, ktorú je možné vykonať s dvomi vektormi rovnakej dimenzie (majú rovnaký počet súradníc), je skalárny súčin. Vstup tejto operácie sú dva vektory, výstup je reálne číslo.
Vďaka skalárnemu súčinu môžeme vypočítať napríklad aký uhol vektory zvierajú, špeciálne či sú na seba kolmé (v takom prípade ich skalárny súčin vyjde nulový).
HoreVektory: násobenie konštantou, súčet, rozdiel
Súčet vektorov
Vektory \vec{u} a \vec{v} sčítame takto: počiatočný bod vektora \vec{v} posunieme do koncového bodu vektora \vec{u}. Súčet vektorov \vec{u} a \vec{v} je vektor \vec{w}, ktorý má počiatočný bod rovnaký ako vektor \vec{u} a koncový bod rovnaký ako vektor \vec{v}. Píšeme: \vec{u}+\vec{v}=\vec{w}
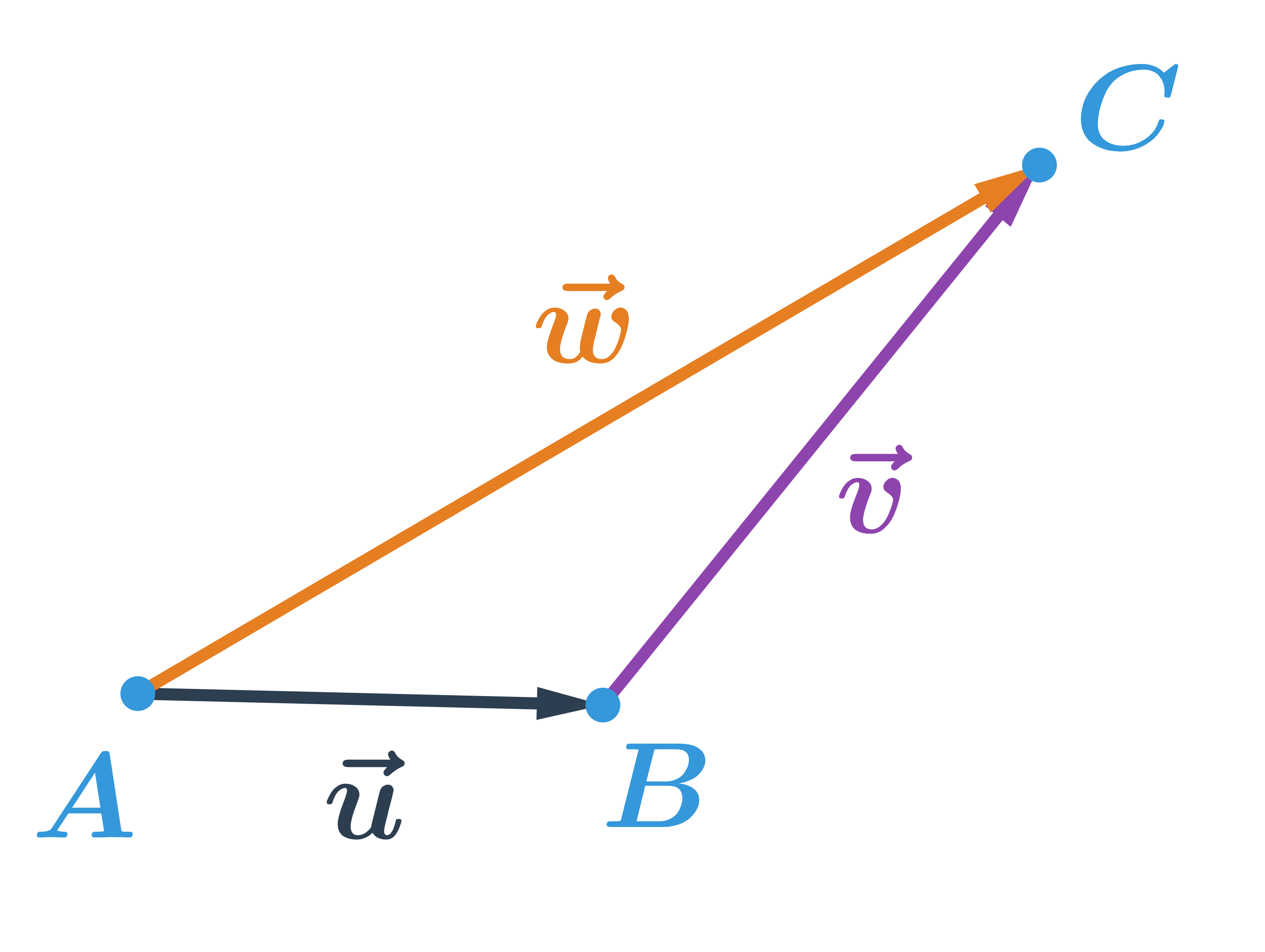
Vektory na obrázku sú označené \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{BC}. Súčet týchto vektorov: \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}
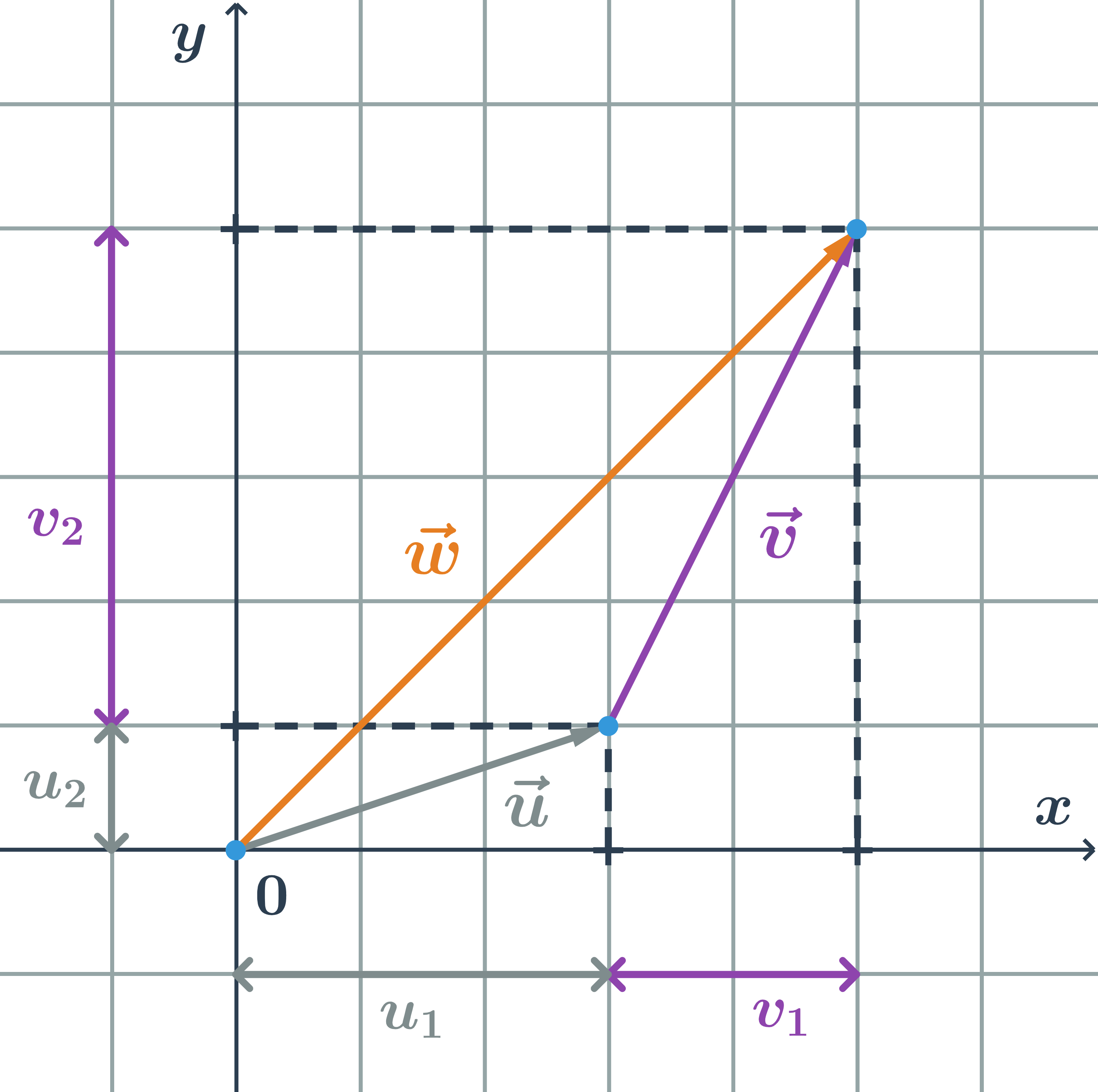
Majme vektory so súradnicami \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2). Potom súčet vektorov \vec{u} a \vec{v} je vektor \vec{w} so súradnicami \vec{w}=(u_1+v_1; u_2+v_2).
Rozdiel vektorov
Rozdiel vektorov \vec{u} a \vec{v} je súčet vektora \vec{u} s vektorom opačným k \vec{v}. Teda:
\vec{u}-\vec{v}=\vec{u}+(-\vec{v})
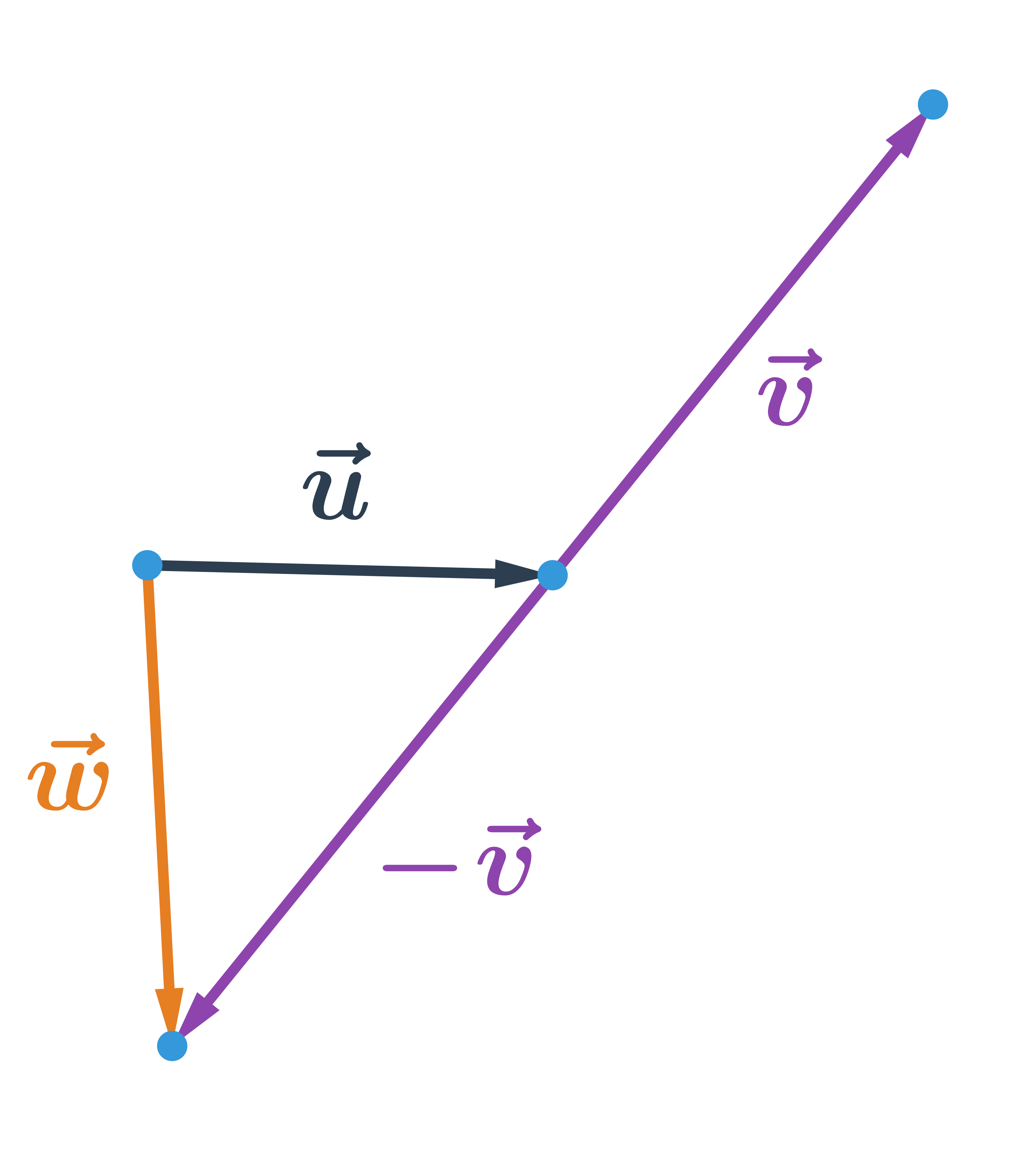
Ak máme súradnice vektorov: \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), potom rozdiel vektorov \vec{u} a \vec{v} je vektor \vec{w}, ktorý má súradnice: \vec{w}=(u_1-v_1; u_2-v_2).
Násobok vektora
Vektor \vec{u} môžeme vynásobiť ľubovoľným reálnym číslom k. Dostaneme vektor \vec{v}, ktorému hovoríme násobok vektora. Píšeme \vec{v}=k \cdot \vec{u}
- Ak k > 0, vektory \vec{u} a k \cdot \vec{u} majú rovnaký smer
- Ak k < 0, vektory \vec{u} a k \cdot \vec{u} majú opačný smer
- Ak k = 0, vektor k \cdot \vec{u} je nulový vektor
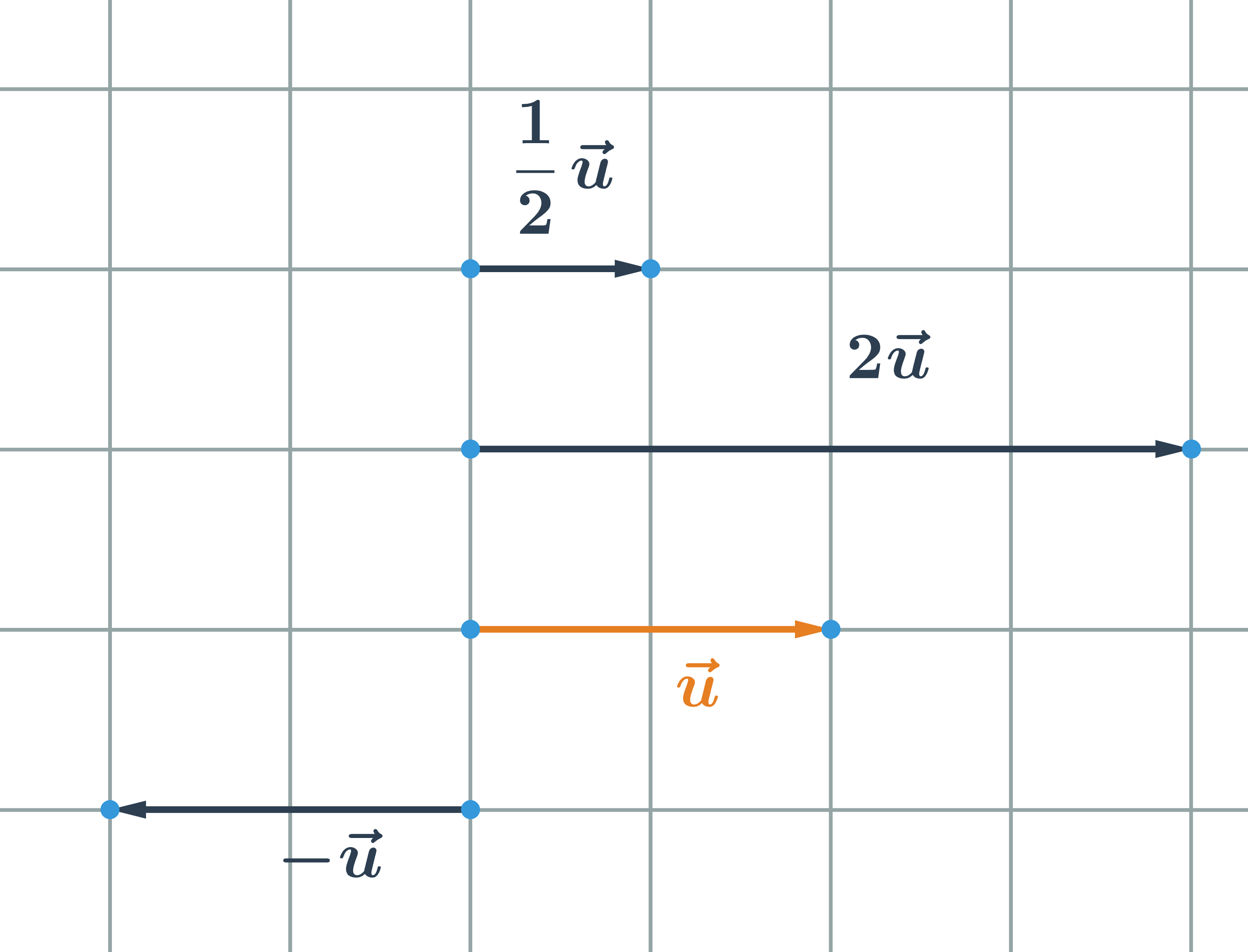
Ak máme súradnice vektora \vec{u}=(u_1;u_2), potom jeho násobok \vec{v}=k \cdot \vec{u} má súradnice \vec{v}=(k \cdot u_1; k\cdot u_2).
Príklad súčtu a násobku vektora graficky
Načrtnite vektor \vec{w}=2\vec{a}-\vec{b}+\vec{c}.
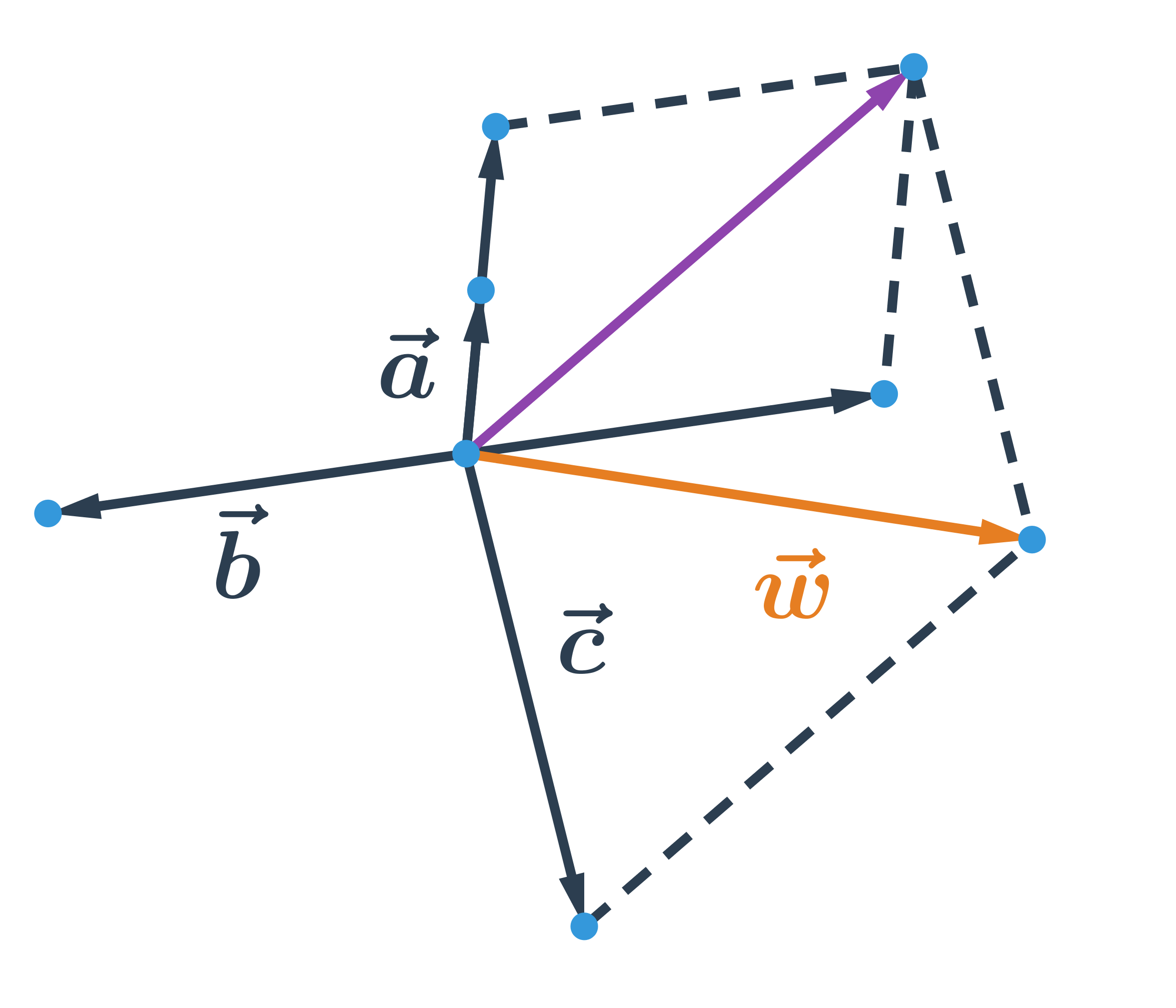
Príklad súčtu a násobku vektora v súradniciach
Sú dané vektory \vec{u}=(2;-3), \vec{v}=(4;1). Určite súradnice vektora \vec{w}=\vec{u}-4\cdot \vec{v}.
- w_1=u_1-4\cdot v_1=2-4\cdot 4=-14
- w_2=u_2-4\cdot v_2=-3-4\cdot 1=-7
Vektory: skalárny súčin
Skalárny súčin vektorov \vec{u} a \vec{v} označujeme \vec{u}\cdot \vec{v}. Pre vektory \vec{u}, \vec{v} s veľkosťami \left| \vec{u} \right| a \left| \vec{v} \right|, ktoré spolu zvierajú uhol \alpha, je skalárny súčin definovaný nasledovne:
\vec{u}\cdot \vec{v}=\left| \vec{u} \right|\cdot\left| \vec{v} \right|\cdot \cos \alpha
Vlastnosti skalárneho súčinu
- Výsledkom skalárneho súčinu dvoch vektorov je číslo (teda skalár).
- Skalárny súčin nulového vektora s ľubovoľným iným vektorom je vždy rovný 0.
- Skalárny súčin vektorov, ktoré sú na seba kolmé, je tiež rovný nule.
Výpočet pomocí súradníc
Ak máme súradnice vektorov \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), potom hodnota ich skalárneho súčinu je:
u_1\cdot v_1+u_2 \cdot v_2
Poznámka: ďalšie typy súčinu vektorov
Okrem skalárneho súčinu existujú aj iné typy súčinu vektorov (vektorový, zmiešaný), preto je dôležité písať o aký súčin ide.Príklad: skalárny súčin vektorov
Určite skalárny súčin vektorov, ak platí: \left| \vec{u} \right|=4, \left| \vec{v} \right|=3 a vektory zvierajú uhol 60°.
- Vzorec: \vec{u}\cdot \vec{v}=\left| \vec{u} \right|\cdot\left| \vec{v} \right|\cdot \cos \alpha
- Dosadíme známe hodnoty: \vec{u}\cdot \vec{v}=4\cdot3\cdot \cos 60°=4\cdot3\cdot\frac{1}{2}=6
Určenie uhla zvieraného dvomi vektormi
S využitím vzťahu pre skalárny súčin môžeme určiť uhol vektorov: \cos \alpha=\frac{\vec{u}\cdot \vec{v}}{\left| \vec{u} \right|\cdot\left| \vec{v} \right|}
Príklad: uhol zvieraný vektormi
Určite uhol vektorov \vec{u}=(3;3) a \vec{v}=(2;0).
- Platí \cos \alpha=\frac{\vec{u}\cdot \vec{v}}{\left| \vec{u} \right|\cdot\left| \vec{v} \right|}.
- Pomocou známych súradníc vektorov vieme vypočítať skalárny súčin \vec{u}\cdot\vec{v} a veľkosti vektorov \left| \vec{u} \right|, \left| \vec{v} \right|:
- \vec{u}\cdot \vec{v}=u_1\cdot v_1+u_2 \cdot v_2=3\cdot2+3\cdot0=6
- \left| \vec{u} \right|=\sqrt{u_1^2 + u_2^2}=\sqrt{3^2+3^2}=\sqrt{18}
- \left| \vec{v} \right|=\sqrt{v_1^2 + v_2^2}=\sqrt{2^2+0^2}=\sqrt{4}
- Dosadíme tieto hodnoty do vzťahu pre výpočet \cos \alpha:
- \cos \alpha =\frac {6}{\sqrt{18}\cdot\sqrt{4}}=\frac{6}{3\sqrt{2}\cdot2}=\frac{1}{\sqrt{2}}
- Uhol vektorov je 60°.


 Slovenčina
Slovenčina Angličtina
Angličtina Informatika
Informatika Vieme to
Vieme to Nemčina
Nemčina Biológia
Biológia Zemepis
Zemepis Chémia
Chémia Fyzika
Fyzika