Logaritmus je inverzná operácia k umocňovaniu. Logaritmus kladného čísla x pri základe a je také reálne číslo y = \log_a(x), pre ktoré platí a^y = x. Číslo a sa nazýva základ logaritmu (báza).
Logaritmus so základom e=2{,}71 828 182... (Eulerovo číslo) sa nazýva prirodzený logaritmus a značí sa väčšinou \ln.
Logaritmus so základom 10 sa nazýva dekadický logaritmus (a niekedy sa značí \mathit{lg}).
Logaritmy majú veľmi široké využitie v mnohých oblastiach matematiky. Historicky sa využívali ako užitočná počítacia pomôcka („logaritmické pravítko“), ktorá využívala fakt, že logaritmus súčinu je súčet logaritmov. Dnes na logaritmy často narazíme napríklad v informatike pri návrhu a analýze algoritmov.
Vlastnosti logaritmov:
- Logaritmus je definovaný len pre kladné čísla.
- Logaritmus so základom 1 nie je definovaný.
- Logaritmus jednotky je nula, \log_a(1)=0.
- Logaritmus s rovnakým základom a argumentom je 1, \log_a{a}=1.
- Logaritmus súčinu je súčet logaritmov, \log_a(x\cdot y)=\log_a{x}+\log_a{y}.
- Logaritmus podielu je rozdiel logaritmov, \log_a\left(\frac{x}{y}\right)=\log_a{x}-\log_a{y}.
- Logaritmus je inverzná funkcia k exponenciálnej funkcii s rovnakým základom, \log_a{x}=y \Leftrightarrow a^y=x.
- Logaritmus mocniny je súčin exponentu a logaritmu základu mocniny, \log_a(x^n)=n\log_a{x}.
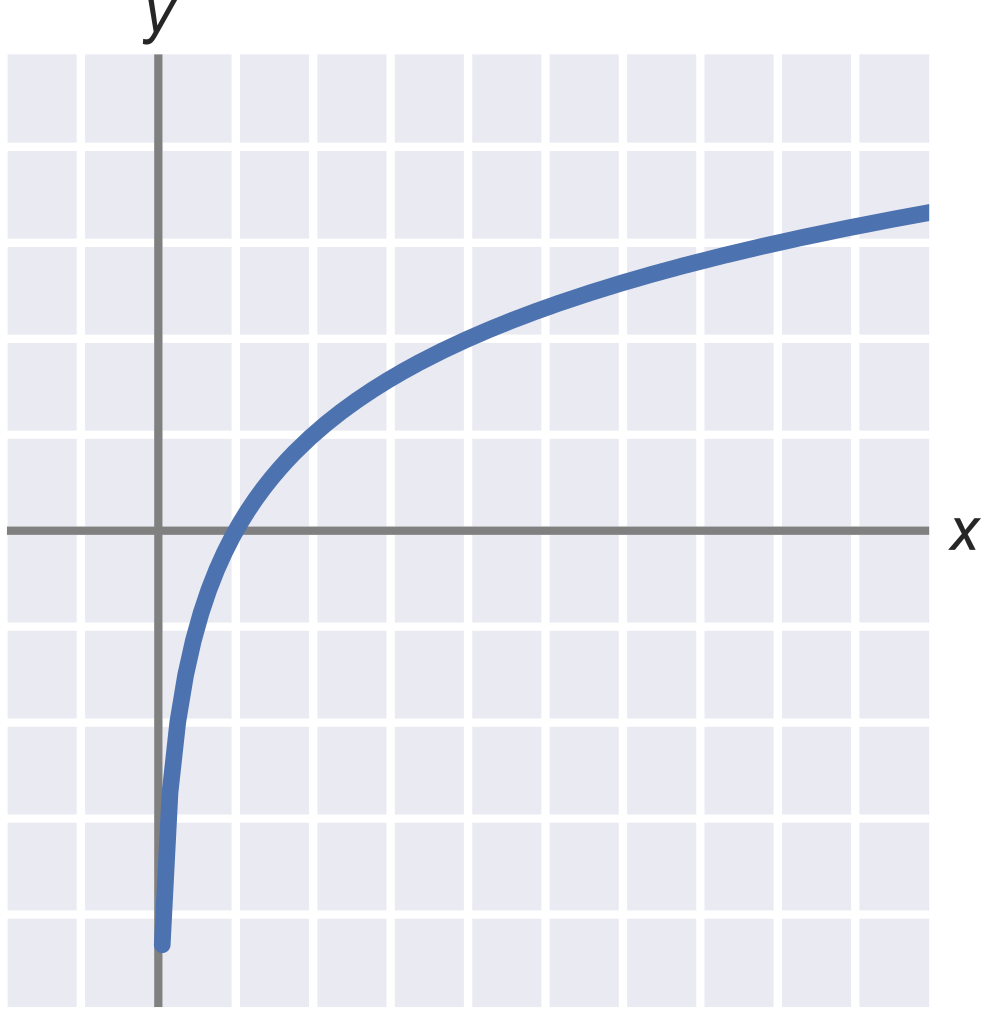
Graf logaritmu so základom 2:
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
Počítanie
Cvičenie, v ktorom píšete odpoveď na klávesnici.
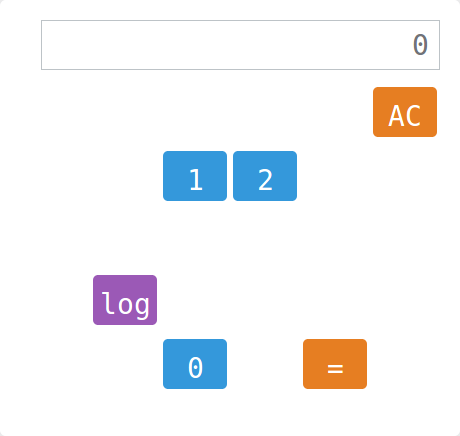
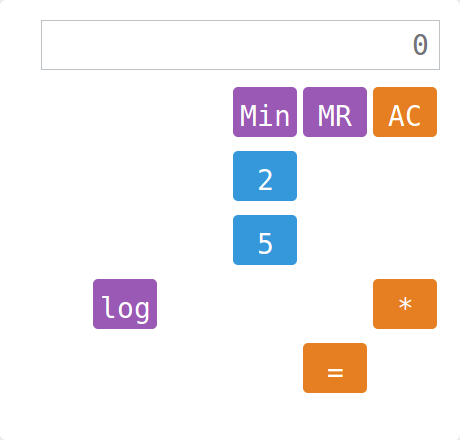
Kalkulačka
Úlohou je vyrobiť na displeji kalkulačky zadané čísla. Problém je, že jej chýbajú niektoré tlačidlá…