Stred úsečky v priestore vypočítame podobne ako stred úsečky v rovine. Vypočítame všetky súradnice stredu ako priemery zodpovedajúcich súradníc krajných bodov.
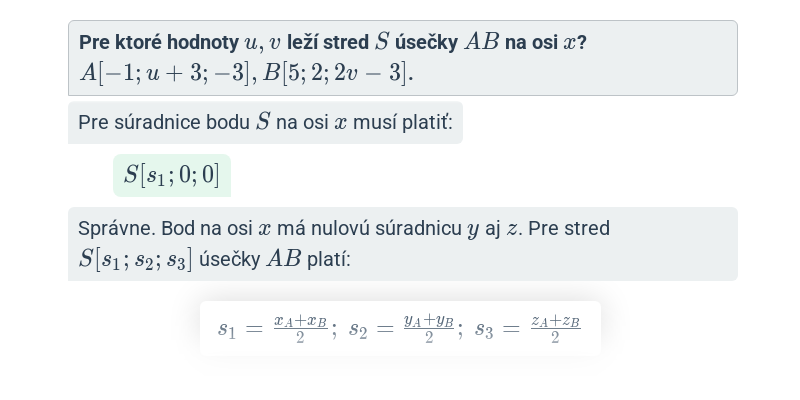
Pre stred S[s_1;s_2;s_3] úsečky AB, kde A[x_A; y_A;z_A], B[x_B; y_B;z_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2} , s_3 = \frac{z_A+z_B}{2}
Príklad: určenie stredu úsečky
Nájdite stred úsečky AB: A[2;1;-3], B[2;-3;3]
Pre súradnice stredu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
Dosadíme súradnice bodov A[2;1;-3], B[2;-3;3].
s_1 = \frac{2+2}{2}=2, s_2 = \frac{1-3}{2}=-1, s_3 = \frac{-3+3}{2}=0
Stred úsečky AB je bod S[2;-1;0]
Príklad: určenie druhého krajného bodu úsečky
Určite súradnice druhého krajného bodu úsečky AB, ak je daný bod A[1;2;4] a jej stred S[1;-3;0].
- Pre súradnice stredu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
- Dosadíme súradnice bodov A[1;2;4], S[1;-3;0].
- 1 = \frac{1+x_B}{2}, -3 = \frac{2+y_B}{2}, 0 = \frac{4+z_B}{2}
- Dopočítame neznáme x_B, y_B, z_B:
\begin{array}{rclcrcr} 2&=&1+x_B &\Rightarrow& x_B&=&1\\ -6&=&2+y_B &\Rightarrow& y_B&=&-8\\ 0&=&4+z_B&\Rightarrow& z_B&=&-4 \end{array}
- Bod B má súradnice [2;-8;-4].
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
Počítanie
Cvičenie, v ktorom píšete odpoveď na klávesnici.