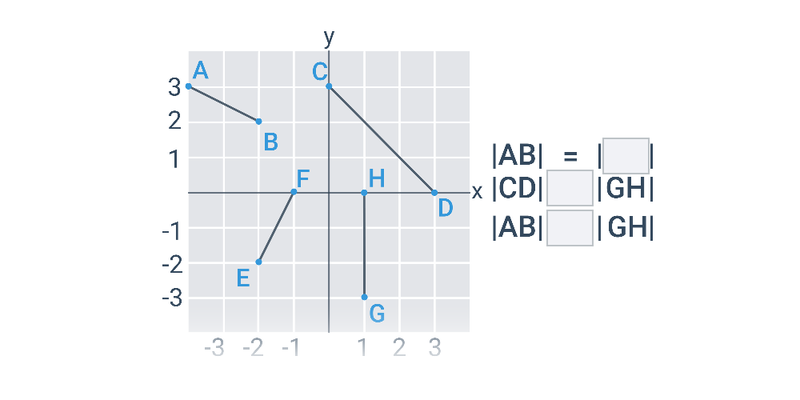
Dĺžku úsečky v rovine vypočítame rovnako ako vzdialenosť bodov v rovine.
Ak sú dané súradnice A[x_A; y_A], B[x_B; y_B], je dĺžka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}
Vzorec vychádza z Pytagorovej vety.
Je nutné počítať rozdiel súradníc v poradí „druhý bod mínus prvý“?
- Nie je. Výrazy x_B-x_A a x_A-x_B nie sú rovnaké. Ale sú opačné a vo vzorci počítame ich druhé mocniny, ktoré sa rovnajú.
- Naviac geometricky je dĺžka úsečky AB rovnaká ako dĺžka úsečky BA.
- Dôvodom zápisu práve v tomto tvare je fakt, že dĺžka úsečky je rovná veľkosti vektora \overrightarrow{AB} a pri vektore sa jeho veľkosť vždy počíta „koncový bod mínus počiatočný“.
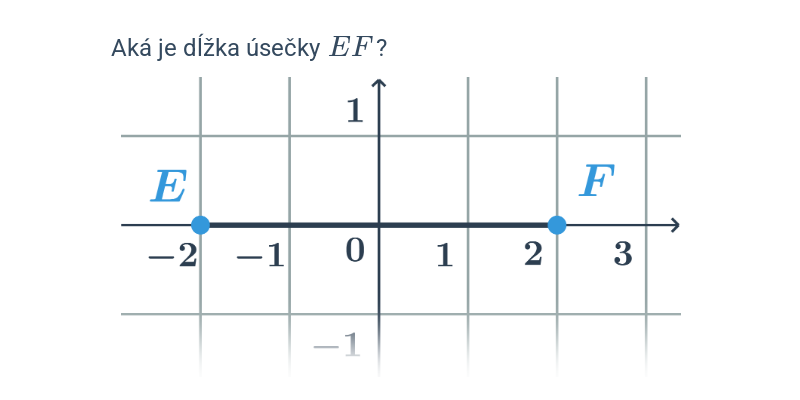
Príklad: Dĺžka úsečky EF: E[0;-1], F[-4;2]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2}
- Dosadíme súradnice bodov E[0;-1] a F[-4;2]: \sqrt{(-4-0)^2 + (2-(-1))^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5
- Dĺžka úsečky je: |EF|=5
Presúvanie
Presúvanie kartičiek na správne miesto. Jednoduché ovládanie, zaujímavé a neotrepané úlohy.
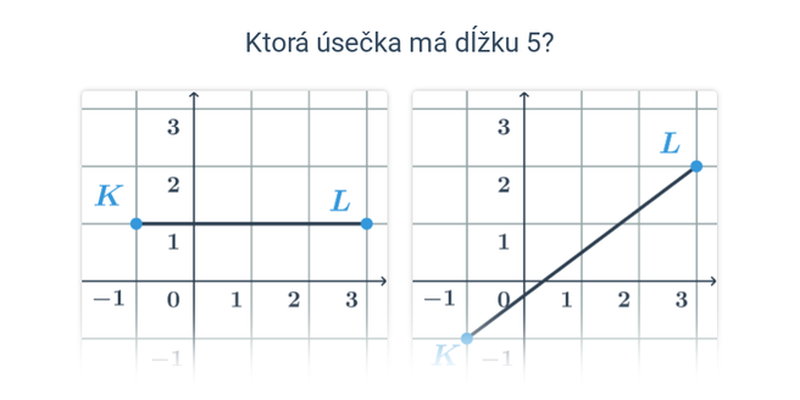
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
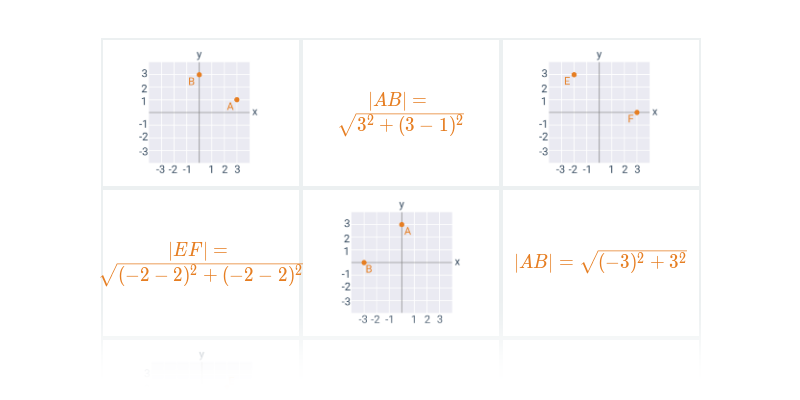
Pexeso
Hľadanie dvojíc, ktoré k sebe patria.
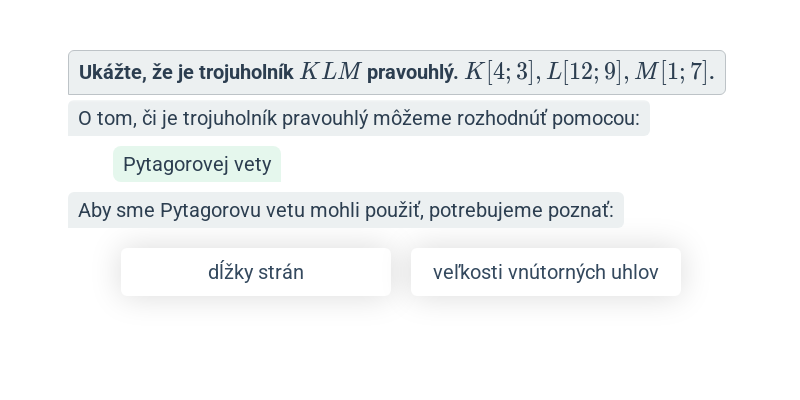
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
Počítanie
Cvičenie, v ktorom píšete odpoveď na klávesnici.