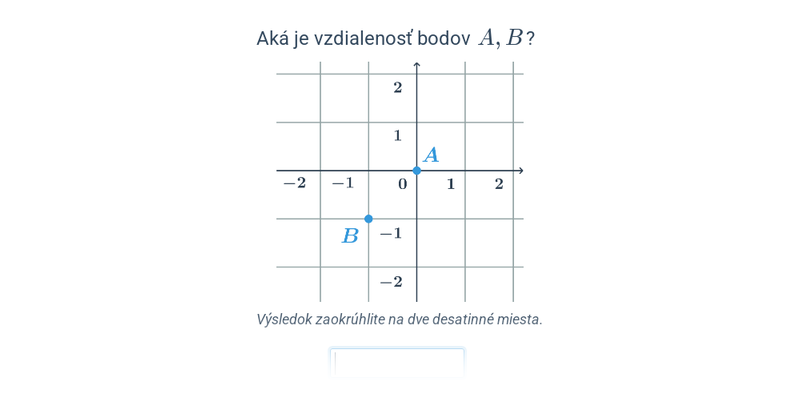
Vzdialenosť bodov v rovine – 9. trieda (9. ročník)

GJW

viemeto.eu/GJW

Vzdialenosť dvoch bodov v rovine môžeme vypočítať, keď poznáme ich súradnice.

Ak sú dané súradnice A=[a_x,a_y], B=[b_x,b_y], je vzdialenosť bodu A od bodu B:

|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2}

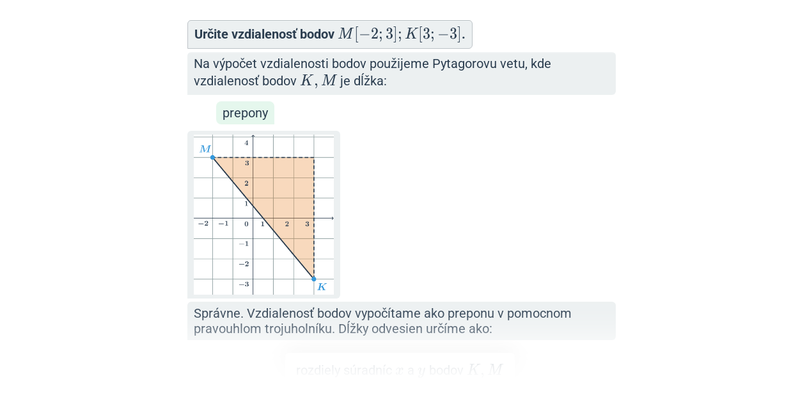
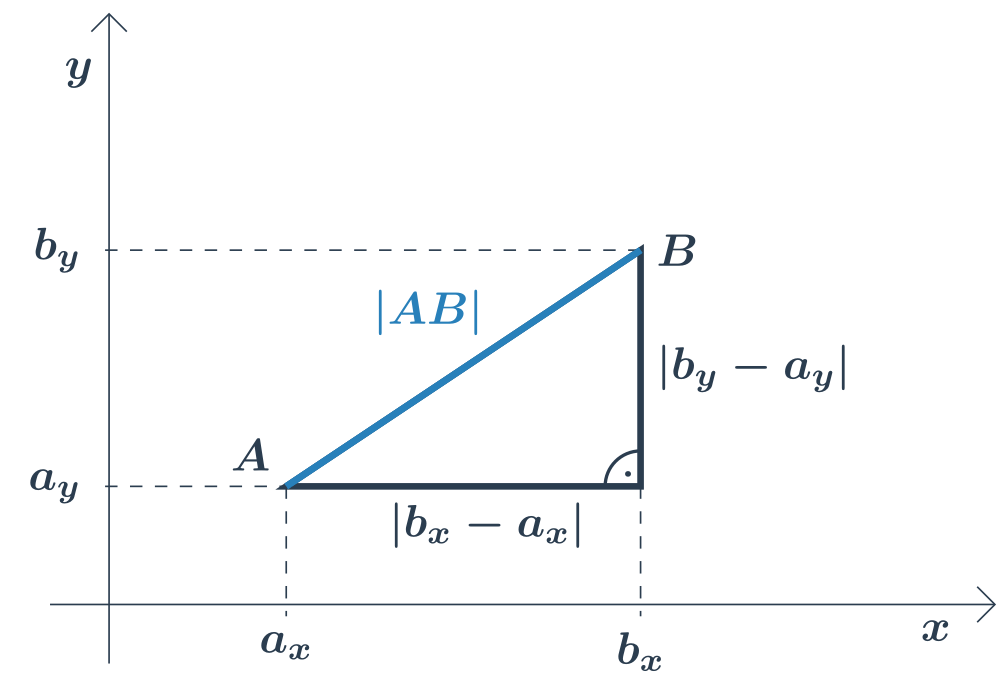
Vzorec vychádza z Pytagorovej vety. Všimnime si pravouhlého trojuholníka s dĺžkami odvesien (b_x-a_x) a (b_y-a_y), ktorého prepona má dĺžku |AB|.

Príklad: vzdialenosť C[0;1],D[4;4]

|CD| = \sqrt{(d_x-c_x)^2 + (d_y-c_y)^2}
Dosadíme súradnice bodov C[0;1] a D[4;4]:
\sqrt{(4-0)^2 + (4-1)^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5
Vzdialenosť je: |CD|=5

Príklad: vzdialenosť M[2;-1], N[-1;-2]

|MN| = \sqrt{(n_x-m_x)^2 + (n_y-m_y)^2}
Dosadíme súradnice bodov M[2;-1] a N[-1;-2]:
\sqrt{(-1-2)^2 + (-2-(-1))^2}=\sqrt{(-3)^2 + (-1)^2}=\sqrt{10}
Vzdialenosť je: |MN|=\sqrt{10}

Súhrn je skrytý.

Presúvanie kartičiek na správne miesto. Jednoduché ovládanie, zaujímavé a neotrepané úlohy.

Vzdialenosť bodov v rovine

Presúvanie • stredné