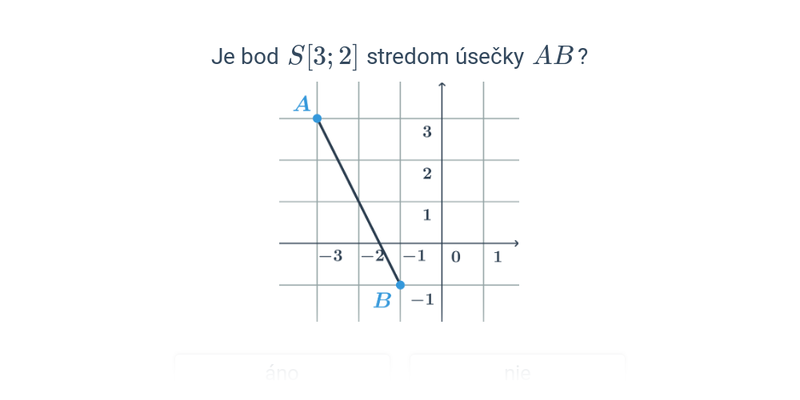
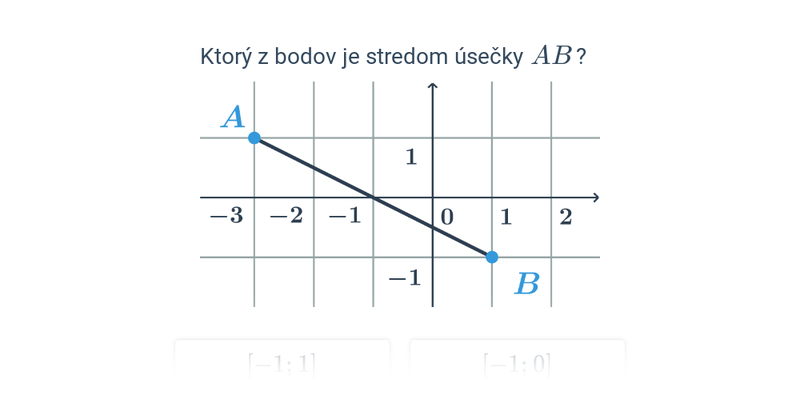
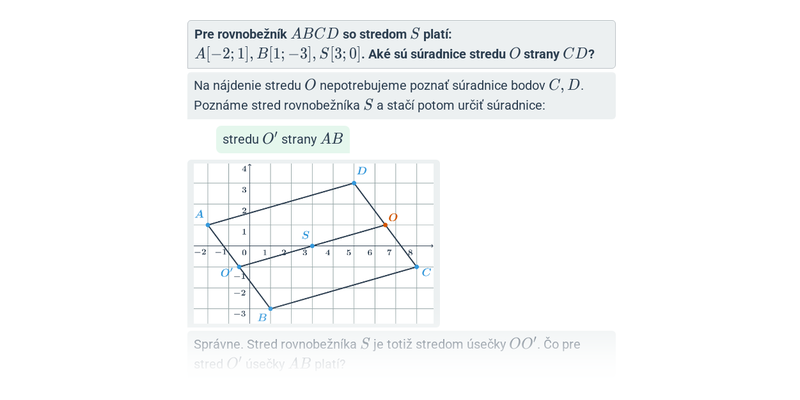
Stred úsečky v rovine

GMG

viemeto.eu/GMG

Stred úsečky delí úsečku na dve rovnaké časti. Ak ležia krajné body úsečky AB na číselnej osi a ich polohám zodpovedajú hodnoty a a b, potom jej stredu S zodpovedá číslo s=\frac{a+b}{2}. Stred úsečky je „priemerom“ jej krajných bodov.

Pre úsečku v rovine bude situácia nasledujúca. 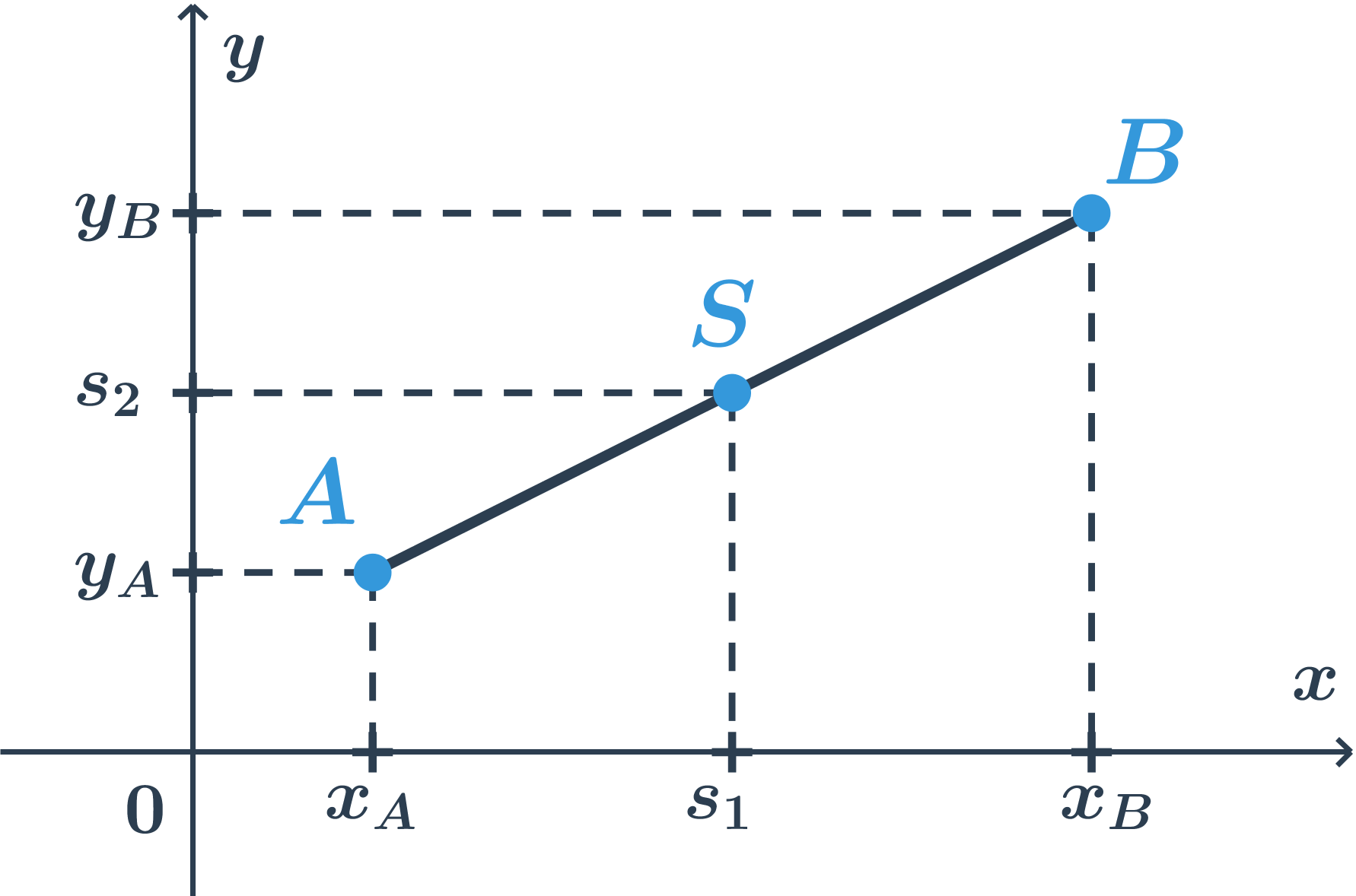Situácia na oboch súradných osách je rovnaká ako predtým. Vypočítame obe súradnice stredu ako priemery zodpovedajúcich súradníc krajných bodov.

Pre stred S[s_1;s_2] úsečky AB, kde A[x_A; y_A], B[x_B; y_B] platí:

s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}

Príklad: určenie stredu úsečky

Nájdite stred úsečky AB: A[6;-1], B[2;3]

Pre súradnice stredu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
Dosadíme súradnice bodov A[6;-1], B[2;3]: s_1 = \frac{6+2}{2}=4, s_2 = \frac{-1+3}{2}=1
Stred úsečky AB je bod S[4;1]

Príklad: určenie druhého krajného bodu úsečky

Určite súradnice druhého krajného bodu úsečky AB, ak je daný bod A[-3;0] a jej stred S[1;3].

Pre súradnice stredu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
Dosadíme súradnice bodov A[-3;0], S[1;3]: 1 = \frac{-3+x_B}{2}, 3 = \frac{0+y_B}{2}
Dopočítame neznáme x_B, y_B: 2=-3+x_B\Rightarrow x_B=5\\ 6=0+y_B\Rightarrow y_B=6
Bod B má súradnice [5;6].

Rozhodovačka

Rýchle precvičovanie výberom z dvoch možností.

Stred úsečky v rovine

Rozhodovačka • stredné

Počítanie

Cvičenie, v ktorom píšete odpoveď na klávesnici.

Stred úsečky v rovine

Počítanie • ľahké

Predchádzajúce

Nadväzujúce

Cvičenie

Stred úsečky v rovine

viemeto.eu/GMG

Rozhodovačka