Ďakujeme za vaše hodnotenie.
Pre logaritmickú funkciu y=\log_ax platí:
- definičný obor D(f)=(0, \infty)
- obor hodnôt H(f)=\R
- je prostá
- nie je periodická
- nie je párna ani nepárna
- nemá maximum ani minimum
- nie je ohraničená
Ďalšie vlastnosti závisia od hodnoty koeficientu a:
- pre a>1 je logaritmická funkcia rastúca
- pre a\in (0,1) je logaritmická funkcia klesajúca
Príklad: vlastnosti funkcie y=\log_2 x
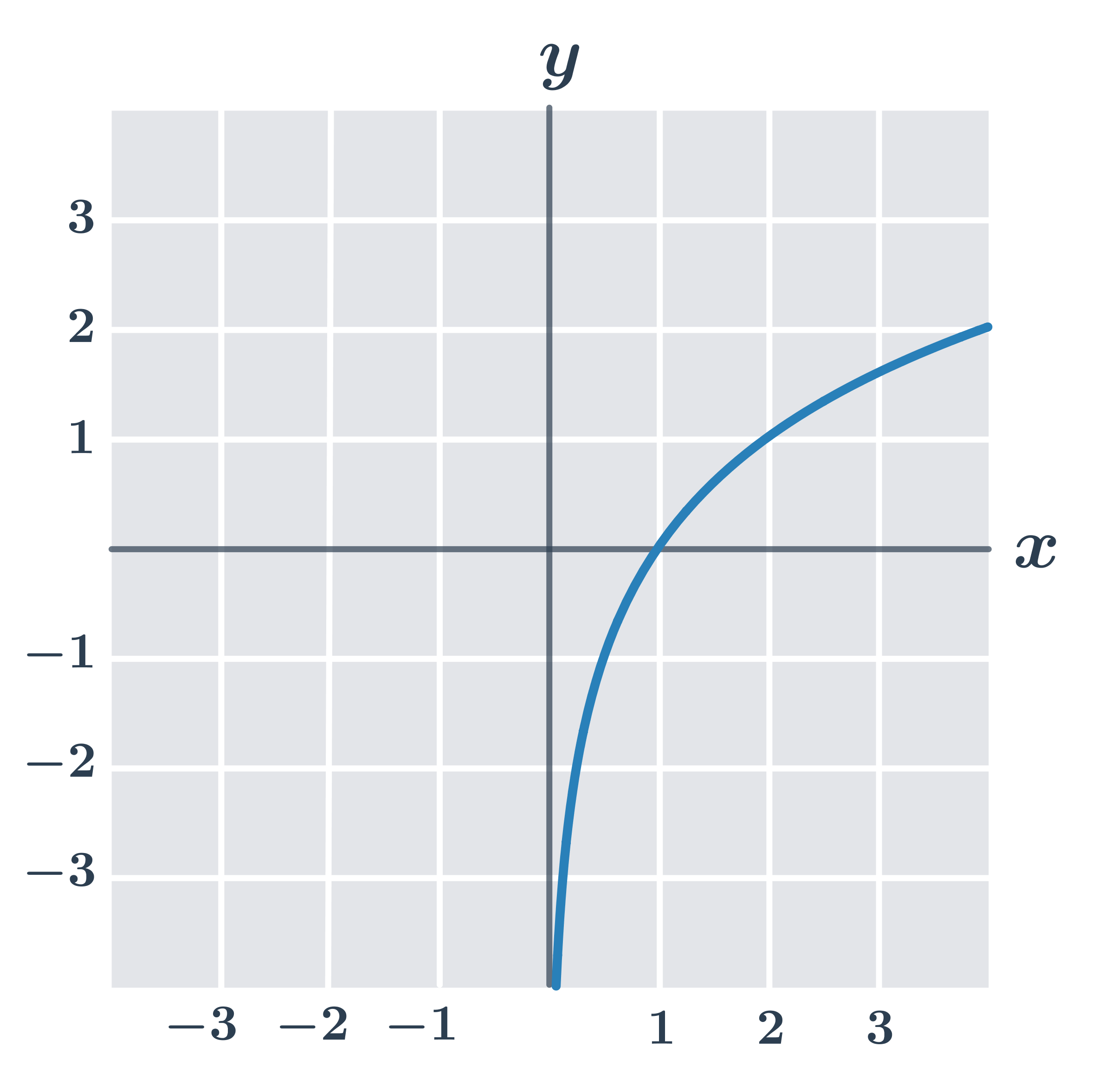
- definičný obor D(f)=(0, \infty)
- obor hodnôt H(f)=\R
- je prostá
- je rastúca
Príklad: vlastnosti funkcie y=\log_{\frac{1}{2}} x
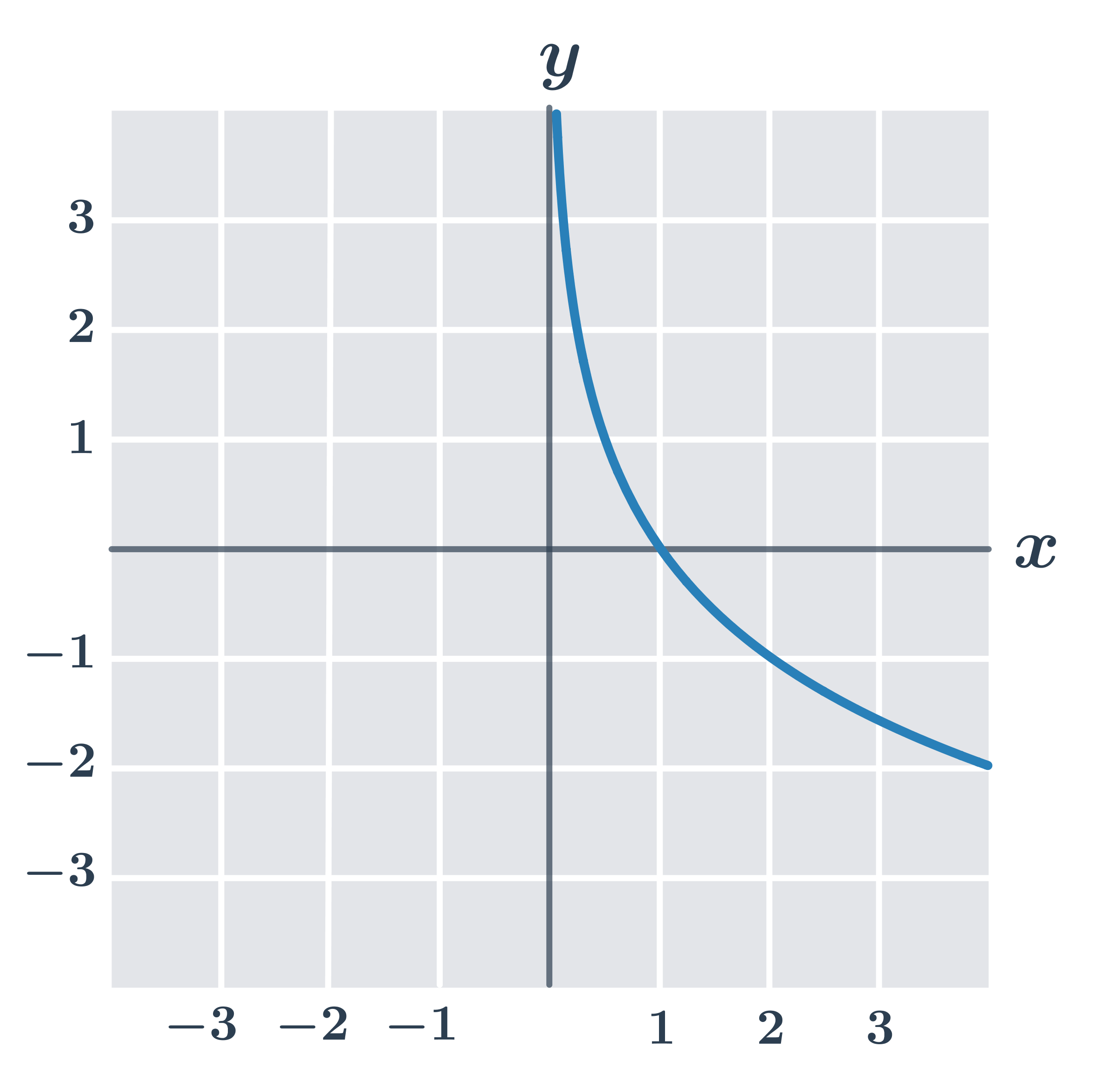
- definičný obor D(f)=(0, \infty)
- obor hodnôt H(f)=\R
- je prostá
- je klesajúca
Príklad: vlastnosti funkcie y=\log_3 (x+2)
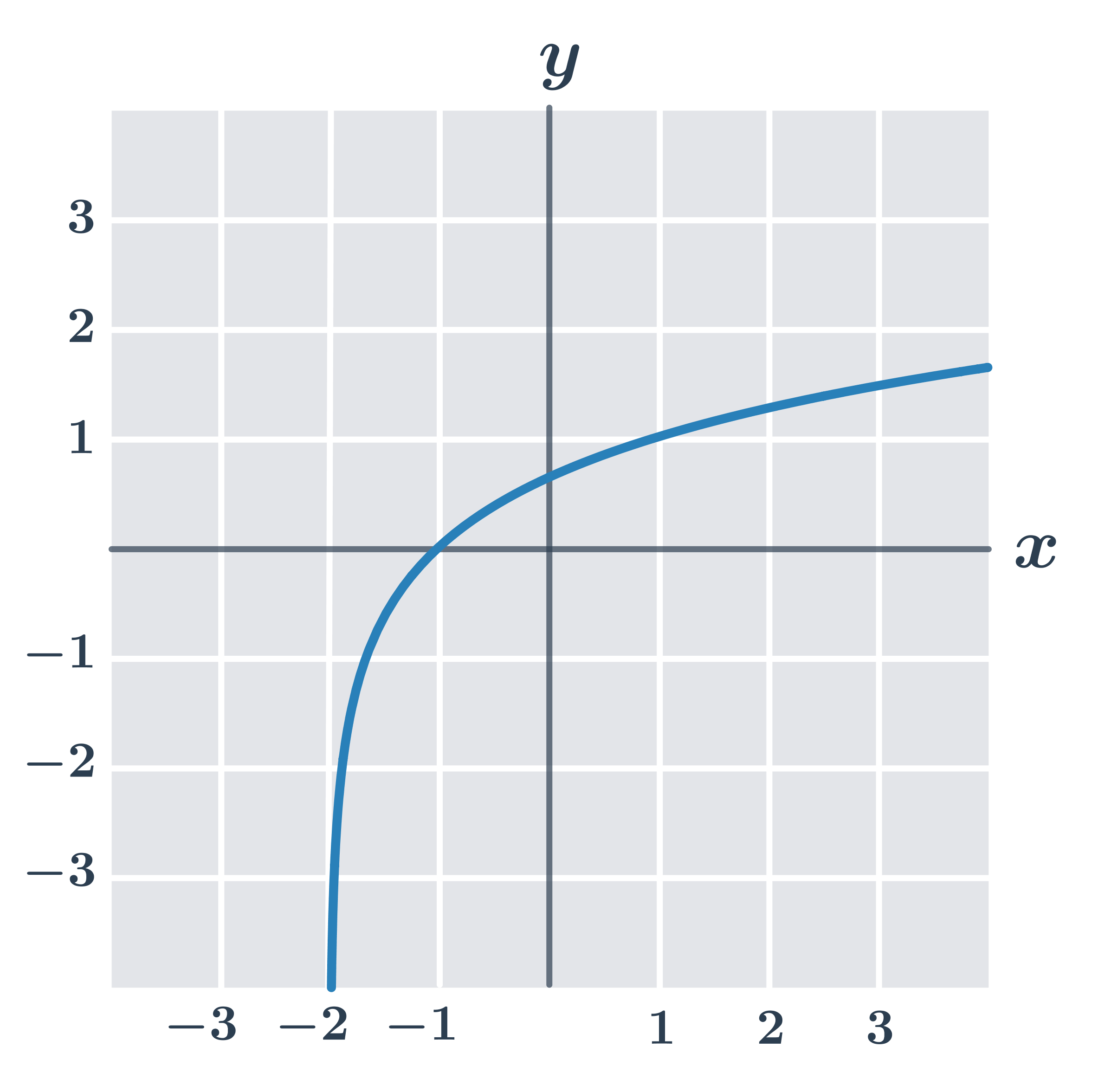
- definičný obor: D(f)=(-2, \infty) … výraz v logaritme musí byť kladný, teda musí platiť: x+2>0\Rightarrow x>-2
- obor hodnôt H(f)=\R
- je prostá
- je rastúca
- priesečník grafu s osou x je bod [-1,0] … nájdeme ako riešenie logaritmickej rovnice: 0=\log_3(x+2). Podľa pravidiel pre počítanie s logaritmami musí platiť: 3^0=x+2\Rightarrow 1=x+2\Rightarrow x=-1
Vysvetlenie mi pomohlo
Vysvetlenie mi nepomohlo
Pre túto tému zatiaľ nie je dostupné žiadne precvičovanie.
