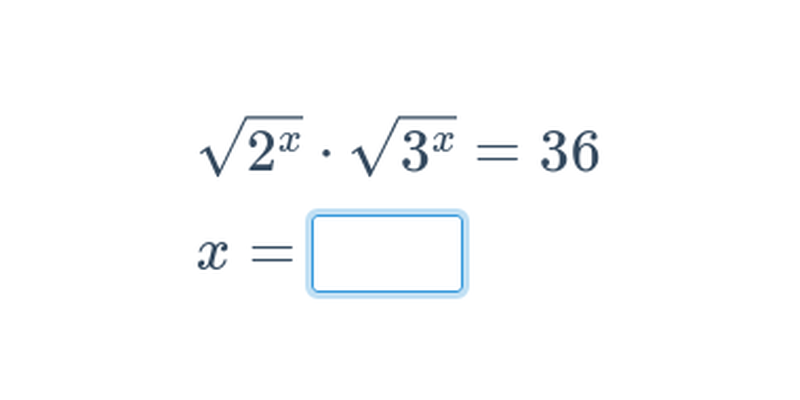Exponenciálne rovnice

F14

viemeto.eu/F14

Exponenciálna rovnica má neznámu v exponente (mocniteli), napr. 3^{2x}-3^x=6.

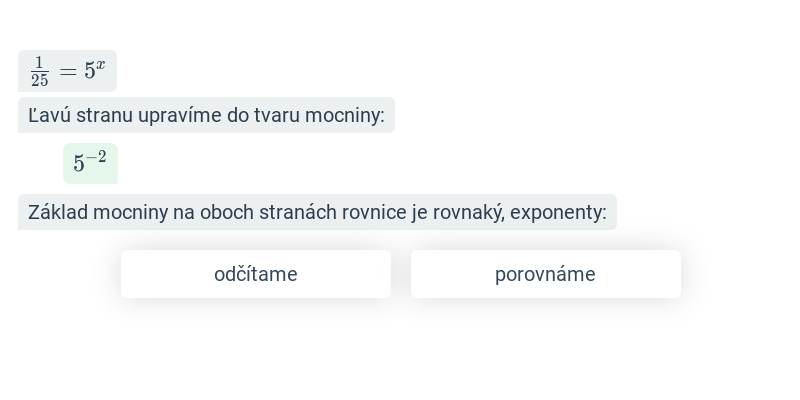
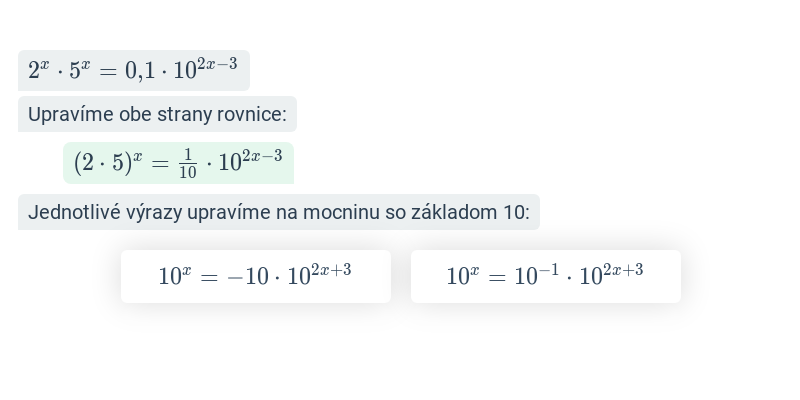
Exponenciálnu rovnicu je možné riešiť rôznymi spôsobmi. Najjednoduchšie je riešenie rovnice s rovnakými základmi. Ak sa nám podarí rovnicu previesť na tvar a^{f(x)} = a^{g(x)}, môžeme sa zbaviť exponenciálnej funkcie a riešiť f(x) = g(x). Zložitejšie spôsoby riešenia exponenciálnych rovníc sú logaritmovanie a substitúcia.