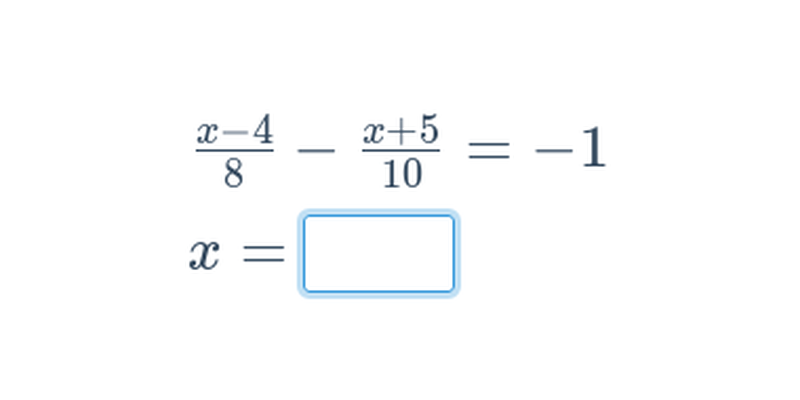Rovnice s lomenými výrazmi

viemeto.eu/FZN

Rovnice s lomenými výrazmi riešime rovnakými postupmi ako základné rovnice.

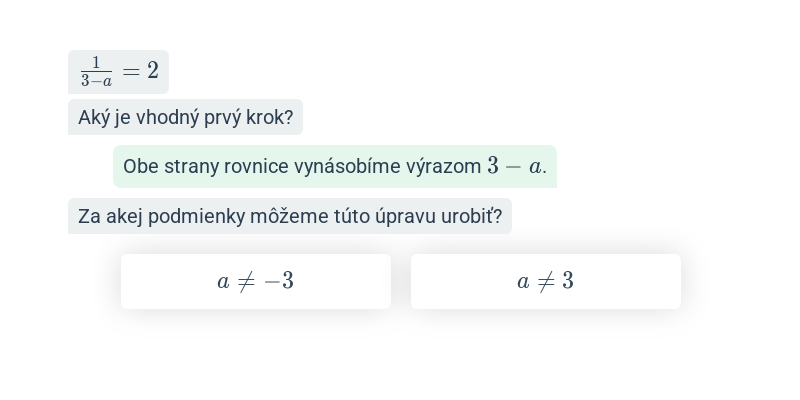
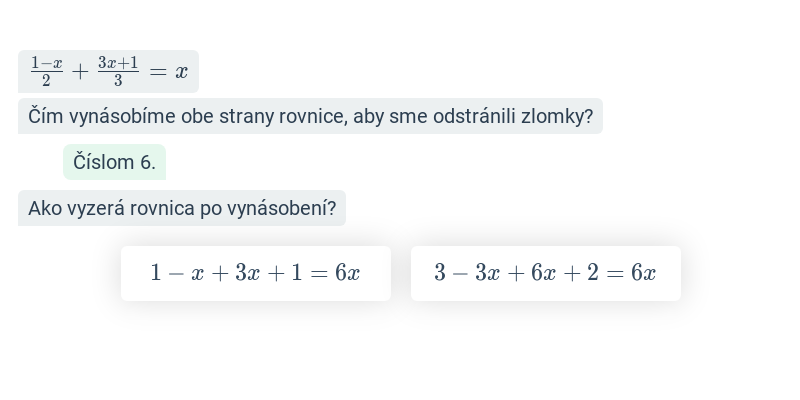
Užitočným (nie však vždy nevyhnutným) prvým krokom býva roznásobenie oboch strán rovnice spoločným násobkom všetkých menovateľov lomených výrazov.

Podmienky riešiteľnosti

Aby lomený výraz dával zmysel, nesmie sa menovateľ rovnať nule. Po vyriešení rovnice teda musíme skontrolovať, že výsledné riešenie túto podmienku spĺňa pre všetky menovatele v rovnici.

Riešený príklad

Zadanie:	\frac{-1}{2} = \frac{x+1}{1-x}
Menovatele sú 2 a 1-x, spoločný násobok je 2(1-x). Roznásobíme teda rovnicu 2(1-x).	\frac{-1}{2}\cdot 2(1-x) = \frac{x+1}{1-x} \cdot 2(1-x)
Krátime obe strany.	(-1)\cdot (1-x) = (x+1)\cdot 2
Roznásobíme obe strany.	x-1 = 2x +2
Prevedieme x na jednu stranu, konštanty na druhú.	x = -3

Krok za krokom

Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.

Rovnice s lomenými výrazmi

Krok za krokom • ľahké

Počítanie

Cvičenie, v ktorom píšete odpoveď na klávesnici.

Rovnice s lomenými výrazmi

Počítanie • ťažké

Predchádzajúce

Nadväzujúce

Cvičenie

Rovnice s lomenými výrazmi

viemeto.eu/FZN

Podmienky riešiteľnosti

Riešený príklad

Krok za krokom