Priamka určená bodom A=[a_1;a_2] a smerovým vektorom \vec{u}=(u_1;u_2) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
Skrátene môžeme vyjadriť p:X=A+t\vec{u}, číslo t nazývame parameter. Ak poznáme dva body A, B ležiace na priamke, smerový vektor je napríklad \vec{u}=\overrightarrow{AB}.
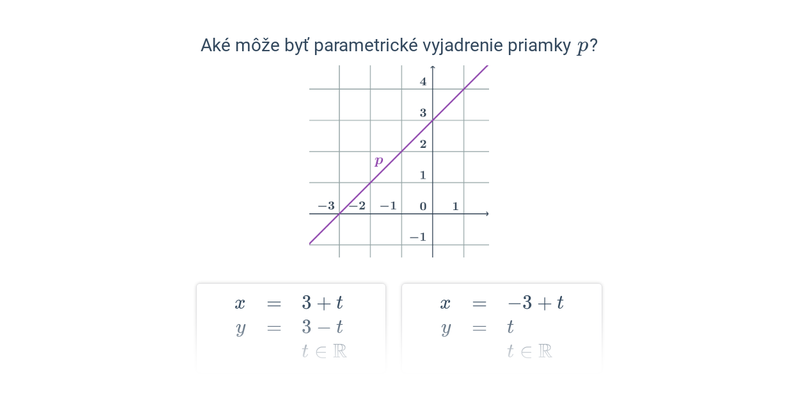
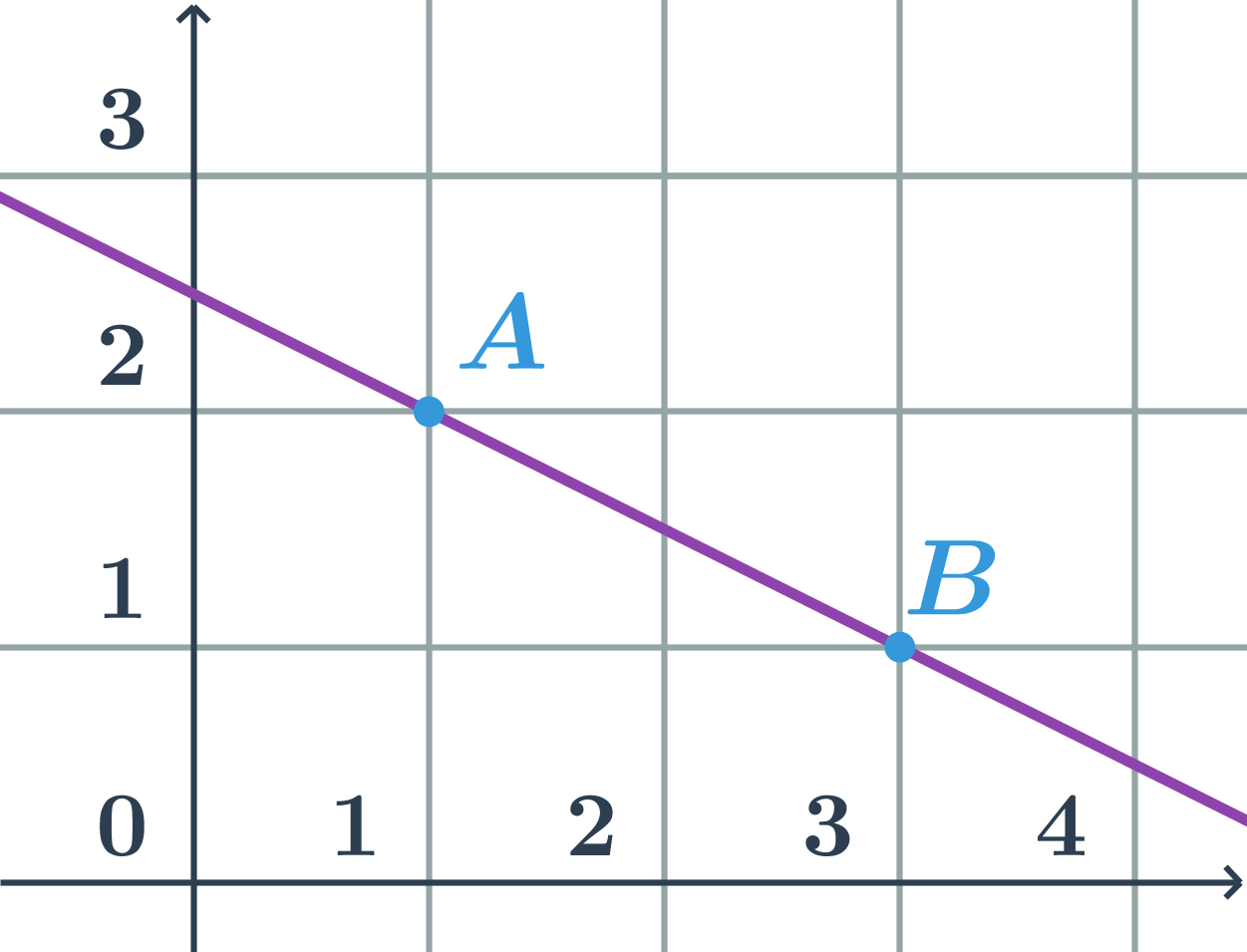
Parametrické rovnice priamky p určenej bodmi A=[1;2] a B=[3;1]
- priamka p je určená bodom A a smerovým vektorom \vec{u}=\overrightarrow{AB}=B-A=(2;-1)
- parametrické rovnice priamky p: \begin{array}{rrl}x&=&1+2t\\y&=&2-t\\&&t\in\mathbb{R}\end{array}
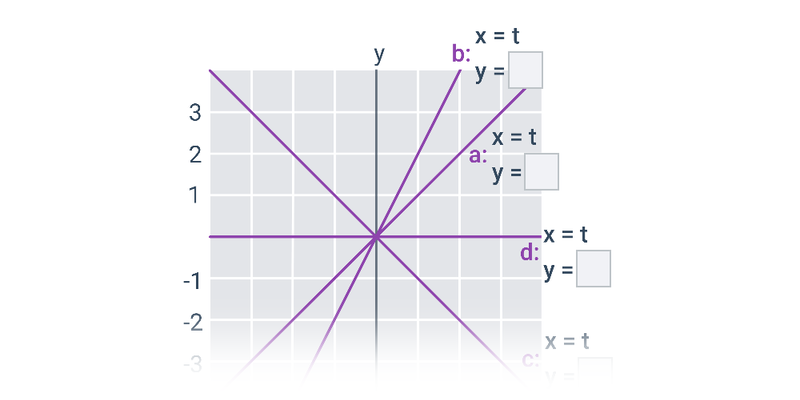
Rôzne parametrické rovnice priamky na obrázku
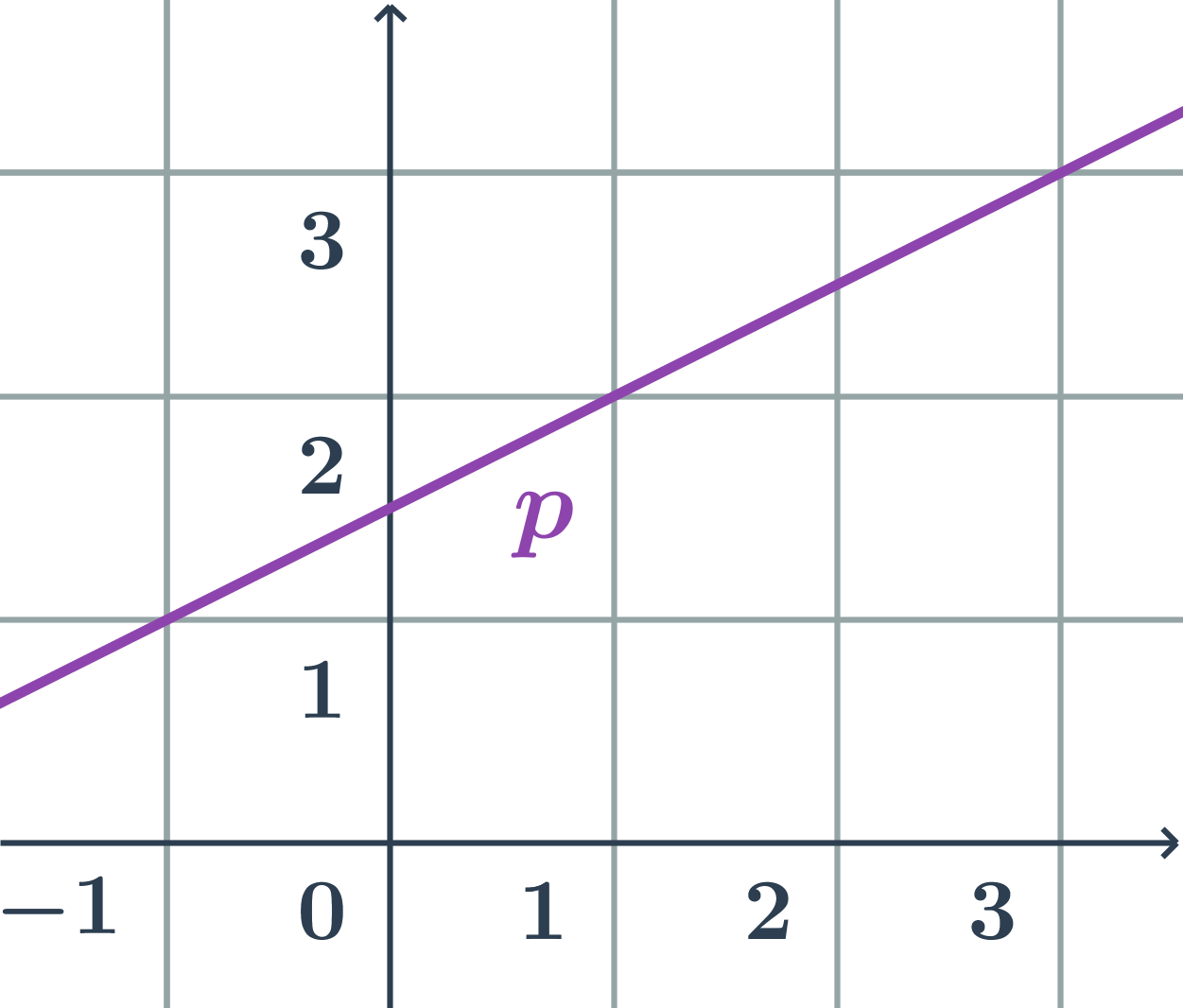
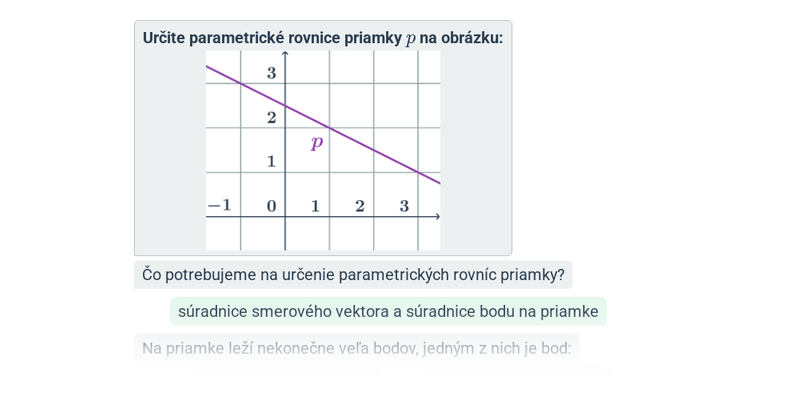
Určíme súradnice smerového vektora a jedného bodu na priamke:
- napríklad: \vec{u}=(2;1), A=[1;2]
- parametrické rovnice priamky p: \begin{array}{rrl}x&=&1+2t\\y&=&2+t\\&&t\in\mathbb{R}\end{array}
Ďalšia možnosť parametrického vyjadrenia:
- \vec{v}=(-4;-2), B=[3;3]
- parametrické rovnice priamky p: \begin{array}{rrl}x&=&3-4t\\y&=&3-2t\\&&t\in\mathbb{R}\end{array}
Na určenie parametrických rovníc môžeme vybrať ktorýkoľvek bod ležiaci na priamke a akýkoľvek zápis súradníc smerového vektora, možností ako parametricky vyjadriť danú priamku je teda nekonečne veľa.
