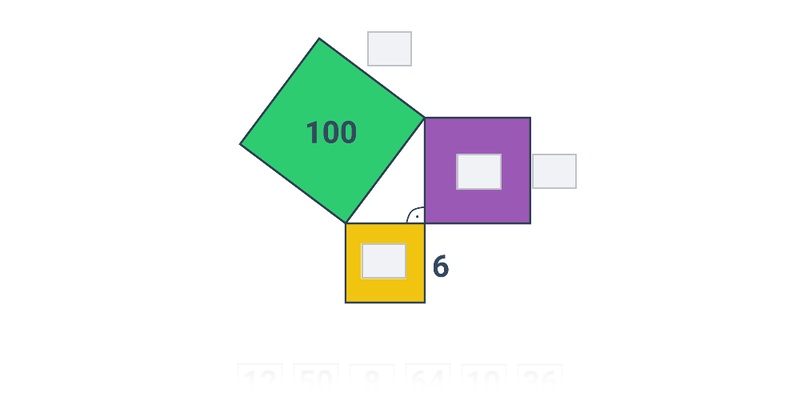
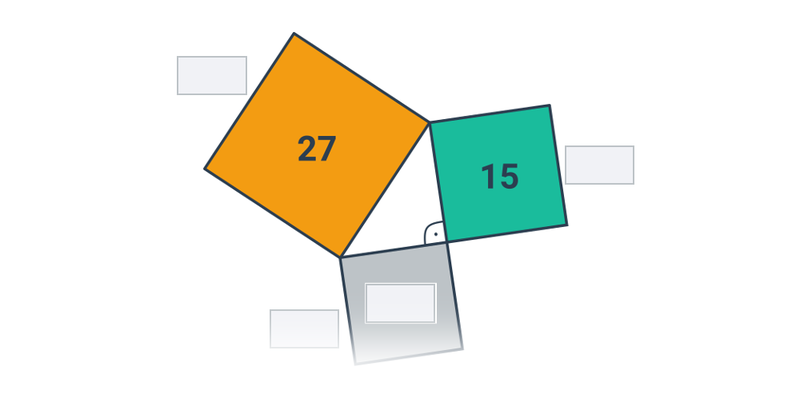
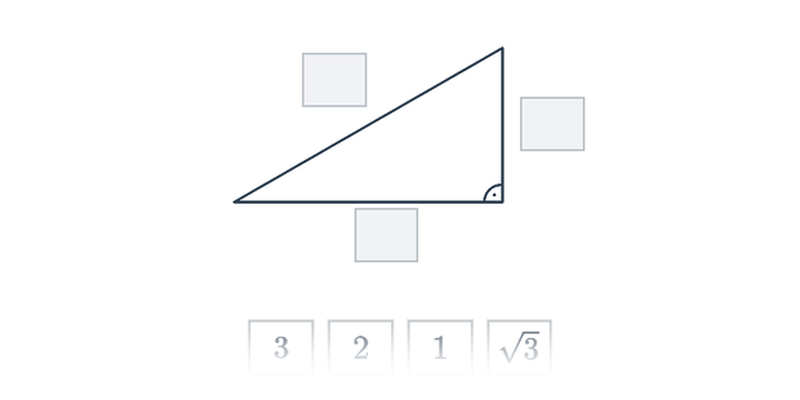
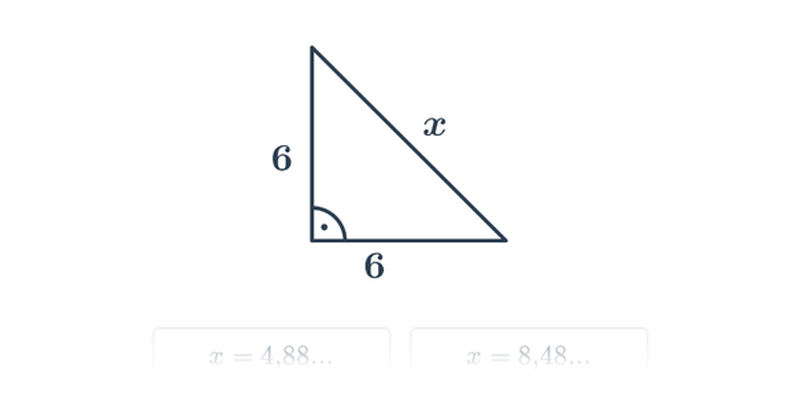
Pytagorova veta umožňuje dopočítať dĺžku tretej strany pravouhlého trojuholníka, pri ktorom poznáme dĺžky dvoch zvyšných strán:
Dĺžka odvesny c = \sqrt{a^2 + b^2}. Ak má pravouhlý trojuholník odvesny s dĺžkou 3 metre a 6 metrov, prepona má dĺžku \sqrt{3^2+6^2} = \sqrt{9+36} = \sqrt{45} \doteq 6,41 metra.
Dĺžka prepony a = \sqrt{c^2-b^2}. Ak má trojuholník preponu s dĺžkou 8 metrov a jedna z odvesien má dĺžku 4 metre, druhá odvesna má dĺžku \sqrt{8^2-4^2} = \sqrt{64-16} = \sqrt{48} \doteq 6,93 metra.
Pytagorejské trojice sú trojice celých čísel, ktoré spĺňajú a^2+b^2=c^2, teda trojuholník s príslušnými dĺžkami strán je pravouhlý. Typickým príkladom pytagorejskej trojice je (3, 4, 5): 3^2 + 4^2 = 9+16 = 25 = 5^2.
Ďalšie príklady pytagorejských trojíc: (5, 12, 13); (8, 15, 17); (7, 24, 25); (20, 21, 29); (9, 40, 41). Medzi pytagorejské trojice patria tiež všetky násobky týchto trojíc, napr. (6, 8, 10); (9, 12, 15); (10, 24, 26). Ak si zapamätáme niektoré základné pytagorejské trojice, predovšetkým najjednoduchšiu trojicu (3, 4, 5), tak nám to môže uľahčiť výpočty.
Presúvanie
Presúvanie kartičiek na správne miesto. Jednoduché ovládanie, zaujímavé a neotrepané úlohy.
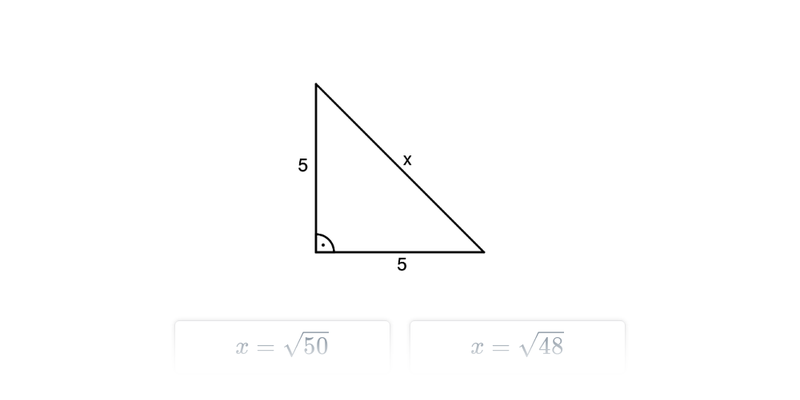
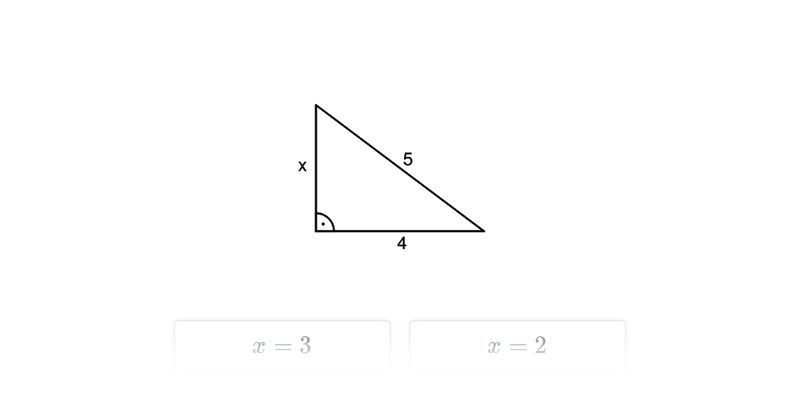
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
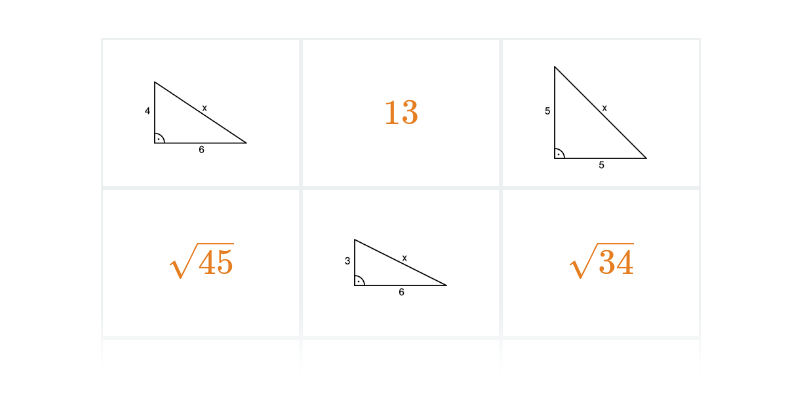
Pexeso
Hľadanie dvojíc, ktoré k sebe patria.
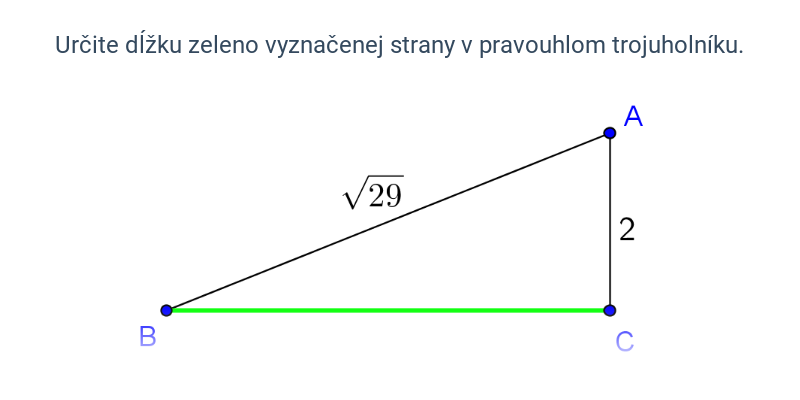
Počítanie
Cvičenie, v ktorom píšete odpoveď na klávesnici.