
Odchýlka dvoch priamok

Odchýlka rovnobežiek je 0^\circ. Odchýlka rôznobežiek je veľkosť ostrého alebo pravého uhla, ktorý priamky zvierajú.
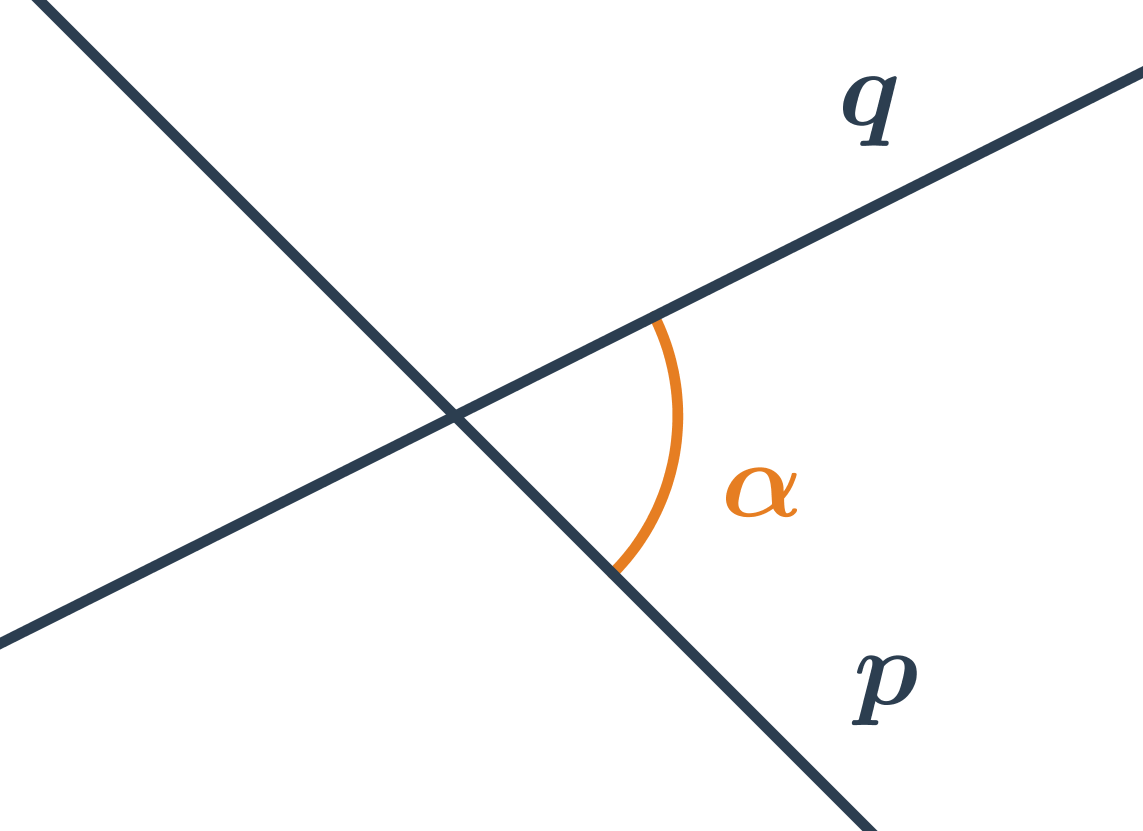
Odchýlku rôznobežiek p a q môžeme vypočítať na základe znalosti smerových alebo normálových vektorov priamok. Vzorec na výpočet uhlov rôznobežiek je podobný ako vzorec na výpočet uhla vektorov.
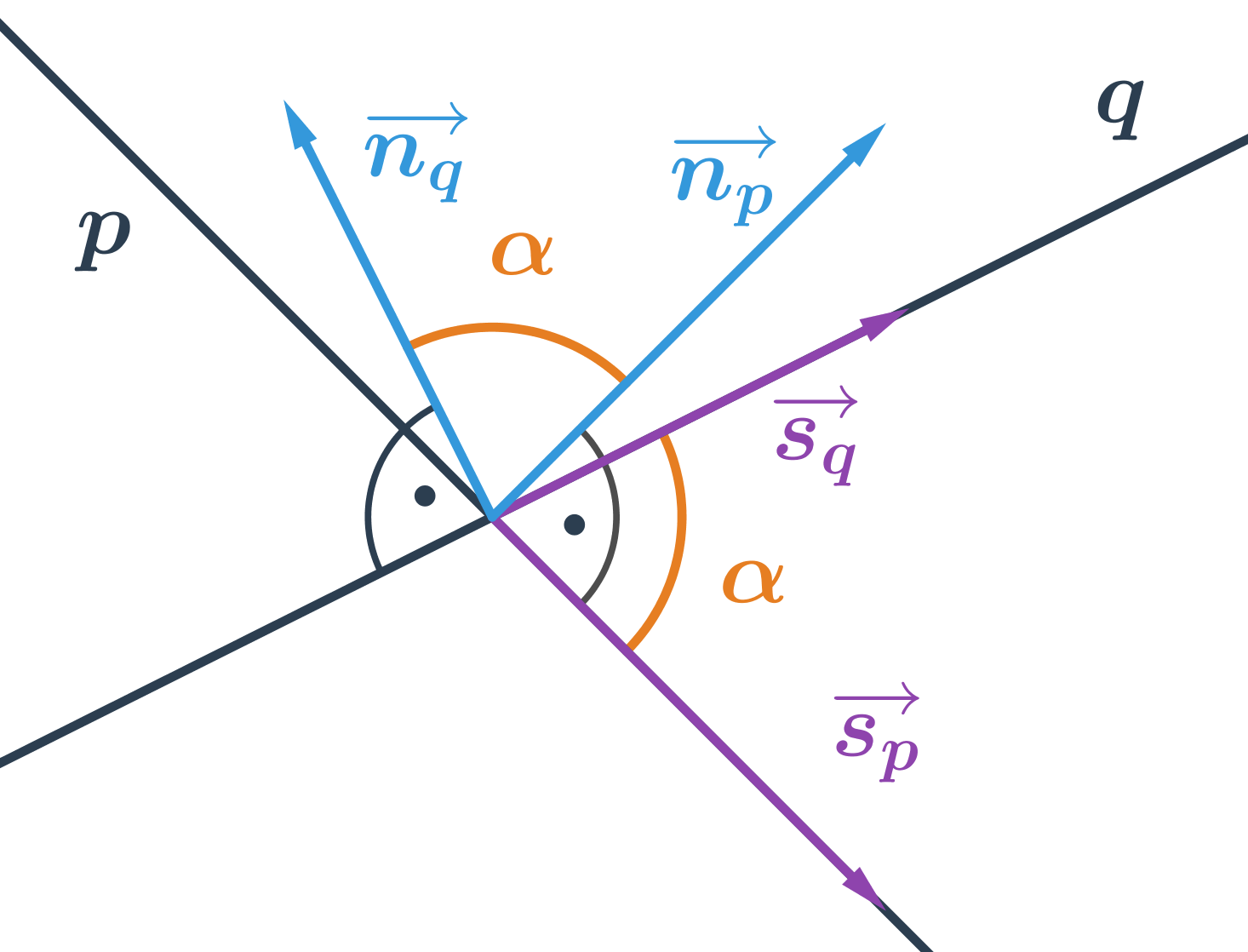
Odchýlka rôznobežiek je uhol \alpha, pre ktorý platí: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|} Vektory \vec{u} a \vec{v} uvedené vo vzorci sú smerové vektory \overrightarrow{s_p} a \overrightarrow{s_q} alebo normálové vektory \overrightarrow{n_p} a \overrightarrow{n_q} priamok p a q.
Pre dve na seba kolmé priamky platí, že ich odchýlka \alpha=90^\circ a teda \cos\alpha=0.
Prečo musí byť vo vzorci pre výpočet odchýlky priamok absolútna hodnota?
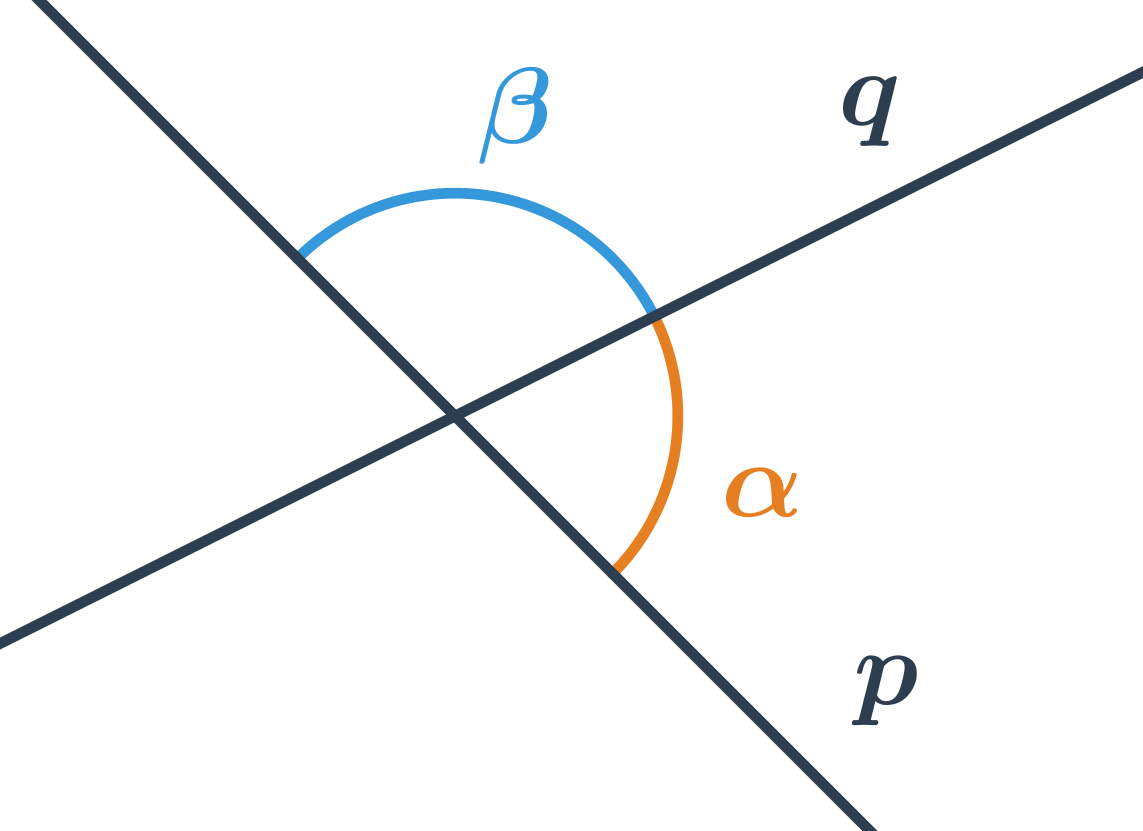
- Odchýlka priamok p a q na obrázku je ostrý uhol \alpha, nie tupý uhol \beta.
- \alpha a \beta sú vedľajšie uhly, pre ktoré je hodnota funkcie \cos opačná, teda: \cos\alpha=-\cos\beta
- Pre uhol \alpha je \cos\alpha > 0, pre \beta je \cos\beta < 0
- Absolútna hodnota vo vzorci nám zaručí, že nájdeme uhol, kde hodnota funkcie \cos je kladná, teda uhol ostrý, ktorý je odchýlkou daných priamok.
Odchýlka priamok a uhly v trojuholníku
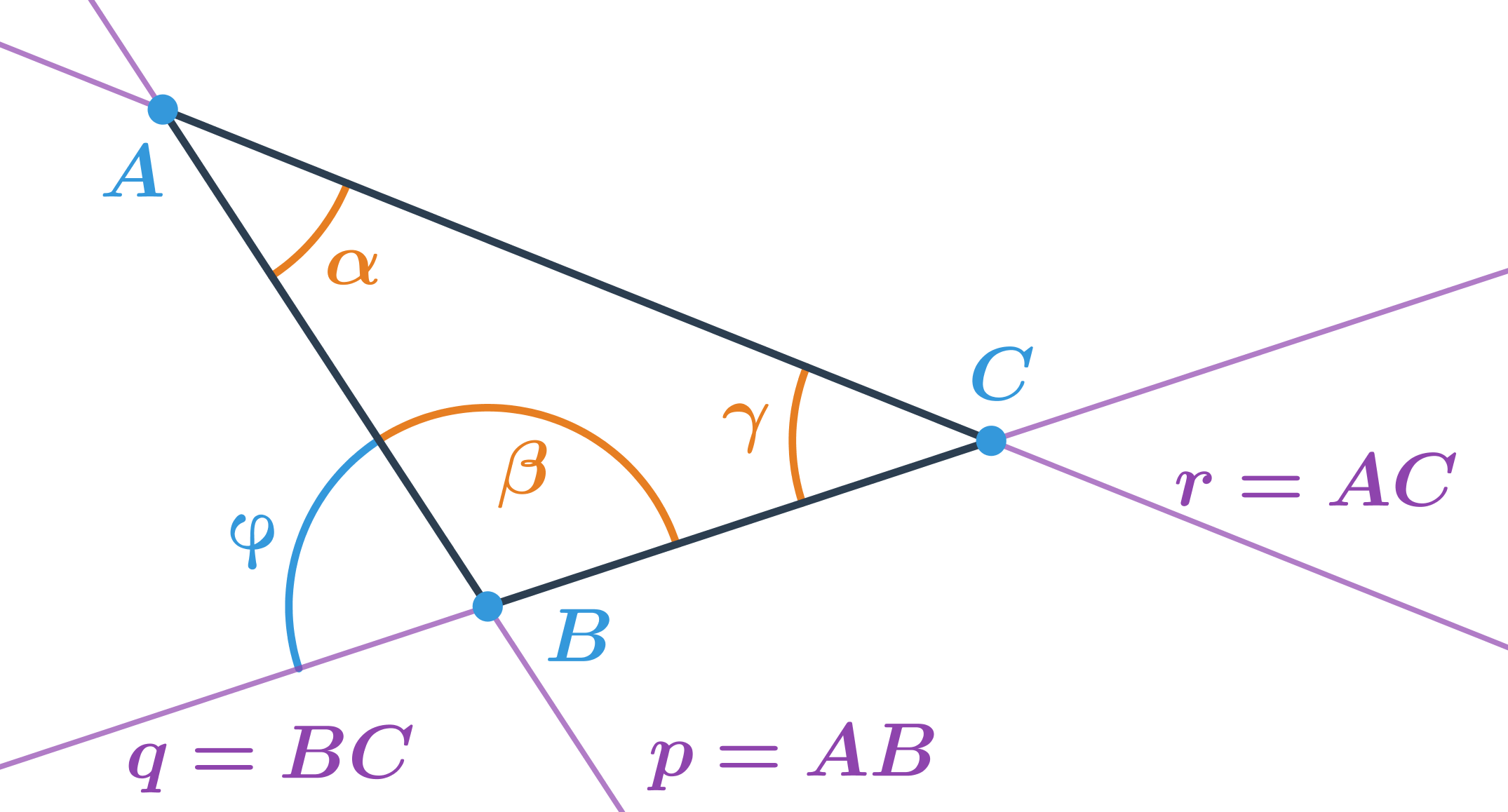
V trojuholníku na obrázku:
- uhol \alpha je menší než 90^\circ a je to odchýlka priamok AB a AC
- uhol \beta je väčší než 90^\circ a nie je to odchýlka priamok AB a BC
- uhol \gamma je menší než 90^\circ a je to odchýlka priamok BC a AC
Veľkosť uhlov v trojuholníku nemusí byť rovnaká ako odchýlka priamok, na ktorých ležia strany trojuholníka. Uhly v trojuholníku počítame ako odchýlku vektorov, ktoré určujú daný uhol. Tento uhol môže byť väčší než 90^\circ, preto využijeme vzorec pre výpočet odchýlky vektorov (vo vzorci nebude absolútna hodnota).
Odchýlka priamok
Určite odchýlku priamok p:x-2y+3=0 a q:2x-y+1=0
- Priamky sú dané všeobecnými rovnicami, preto pre výpočet ich odchýlky využijeme normálové vektory: \overrightarrow{n_p}=(1;-2) a \overrightarrow{n_q}=(2;-1)
- Dosadíme do vzorca: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|}=\frac{\left| 1\cdot2+(-2) \cdot(-1) \right|}{\sqrt{1^2+(-2)^2}\cdot\sqrt{2^2+(-1)^2}}=\frac{4}{\sqrt{5}\cdot \sqrt{5}}=\frac{4}{5}
- Pomocou funkcie cos^{-1} na kalkulačke dopočítame odchýlku: \alpha=36^\circ
Zatvoriť













