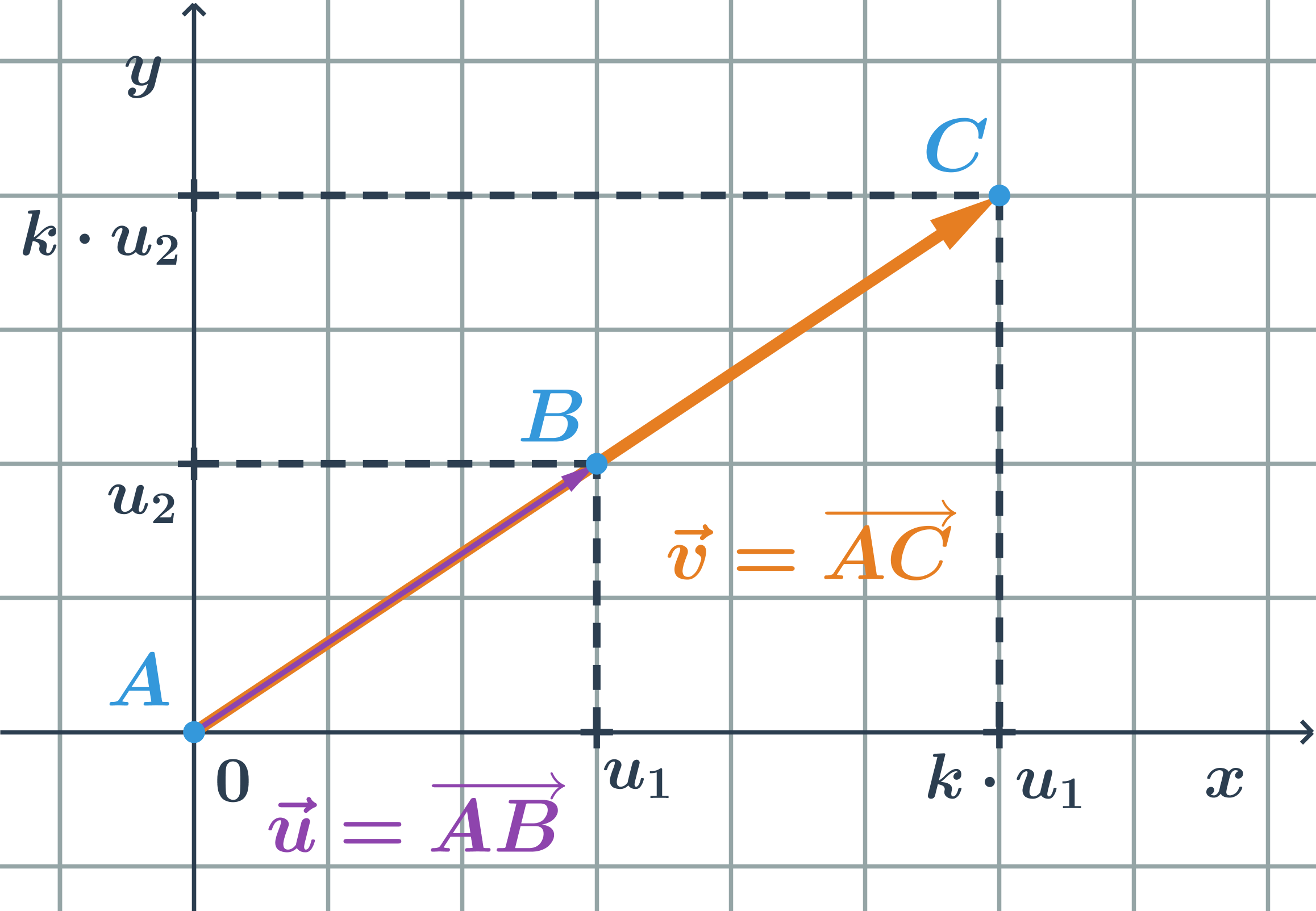Slovenčina
Angličtina
Informatika
Vieme to
Nemčina
Biológia
Zemepis
Chémia
Fyzika
Aritmetika
Zlomky, percentá, desatinné čísla
Geometria
Elementárna algebra
Funkcie
Jednotky, miery
Diskrétna matematika
Finančná gramotnosť
Rozhodovačka
Pexeso
Krok za krokom
Počítanie
Grafár
Porozumenie
Označovanie
Presúvanie
Mriežkovaná
Rozdeľovačka
Pokazená kalkulačka
Roboti
Strieľačka
Príšerky
Preteky
Územia
Tipovačka
Tímovka
Môj účet
Odhlásiť sa
Počítanie
Geometria
Precvičujte neobmedzeneVáš denný počet odpovedí je obmedzený. Pre navýšenie limitu alebo prístup do svojho účtu s licenciou sa prihláste.
Prihlásiť sa
GKHQR kód
Kód / krátka adresa
Skopírujte kliknutím.
Vzájomná poloha vektorov
Opačné vektory sú vektory, ktoré majú rovnakú dĺžku a opačnú orientáciu. K vektoru \vec{u}=(u_1;u_2) je opačný vektor \vec{v}=(-u_1;-u_2)
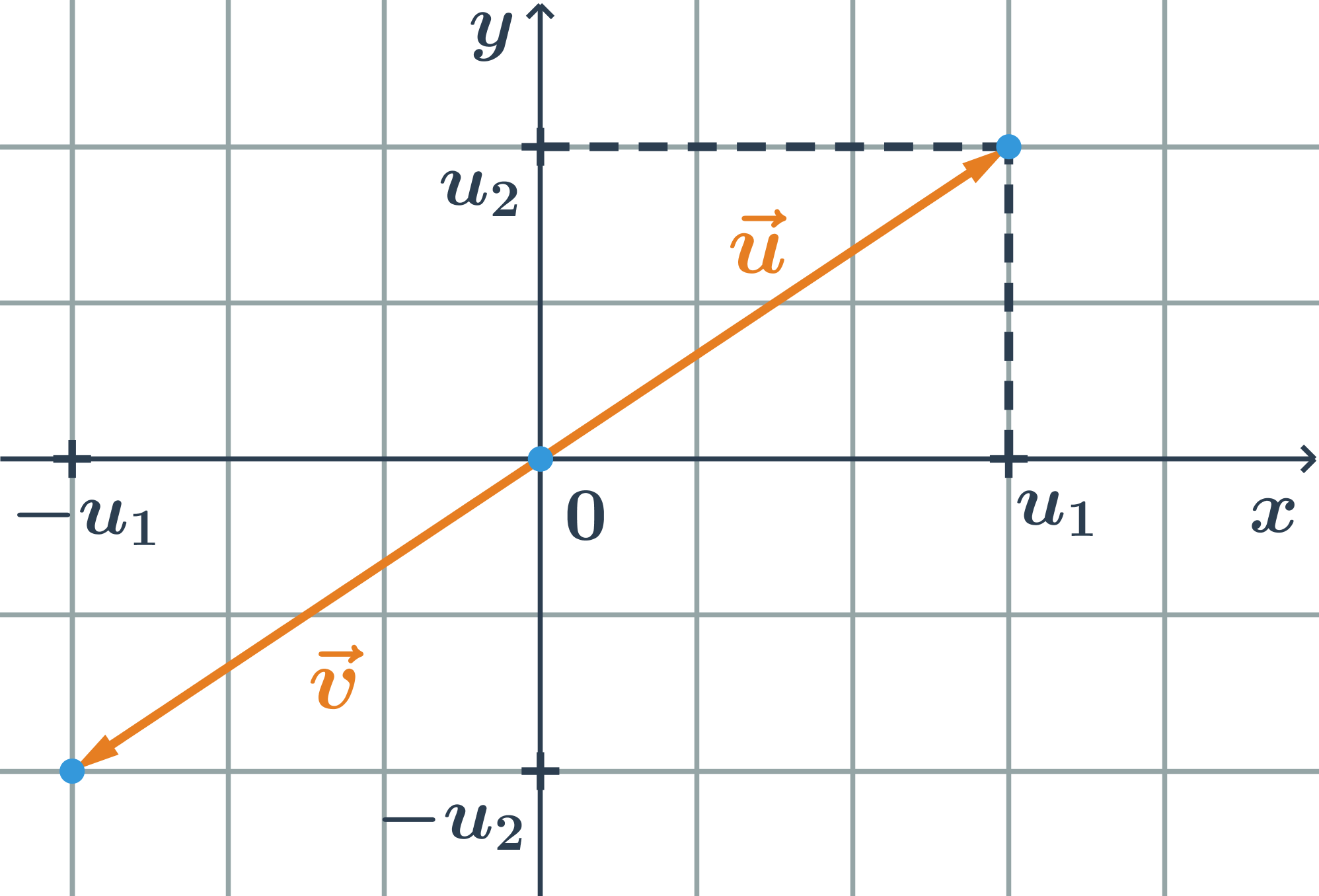
Príklad opačný vektor
- Určite opačný vektor k vektoru \vec{u}=(3;-1).
- Opačný vektor \vec{v} k vektoru \vec{u} má súradnice: (-u_1;-u_2)=(-3;1)
Kolineárne vektory sú vektory, ktoré môžeme umiestniť na jednu priamku. S vektorom \vec{u}=(u_1;u_2) je kolineárny každý vektor \vec{v}=(k\cdot u_1;k \cdot u_2), kde k je reálne nenulové číslo. Pre k>0 majú vektory rovnaký smer, pre k<0 majú vektory opačný smer.
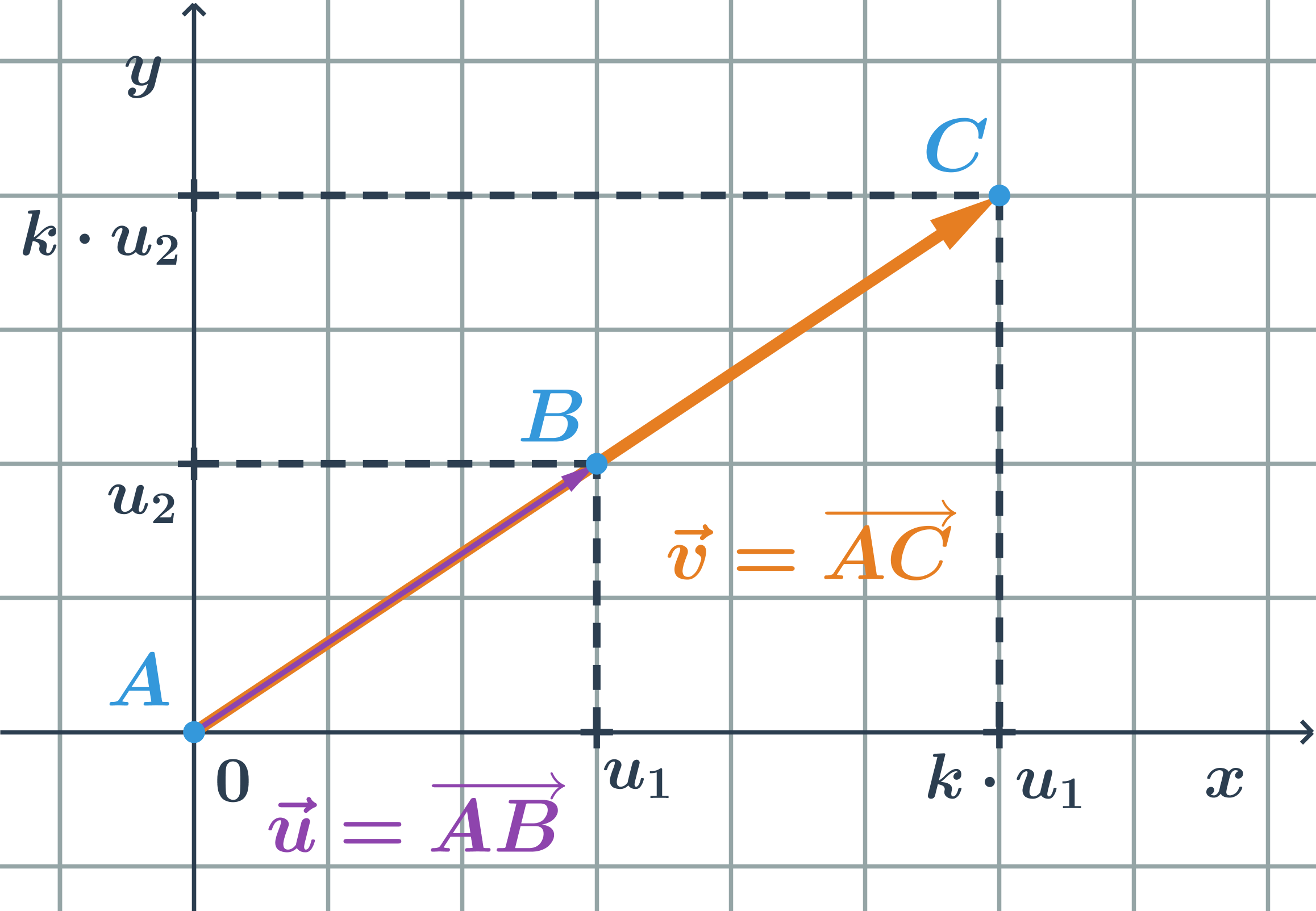
Príklad kolineárny vektor
- Doplňte súradnicu vektora \vec{v}=(v_1;3) tak, aby bol kolineárny s vektorom \vec{u}=(2;-1).
- Pre druhú súradnicu platí: v_2=3, u_2=-1, teda v_2= (-3) \cdot u_2
- Vidíme, že k=-3 je záporné, teda \vec{u} a \vec{v} majú opačnú orientáciu
- Pre prvú súradnicu musí platiť: v_1= (-3) \cdot u_1= (-3)\cdot2=-6.
Kolmé vektory sú vektory, ktoré zvierajú pravý uhol Na vektor \vec{u}=(u_1;u_2) je kolmý každý vektor \vec{v}=(-k\cdot u_2;k \cdot u_1), kde k je reálne nenulové číslo.
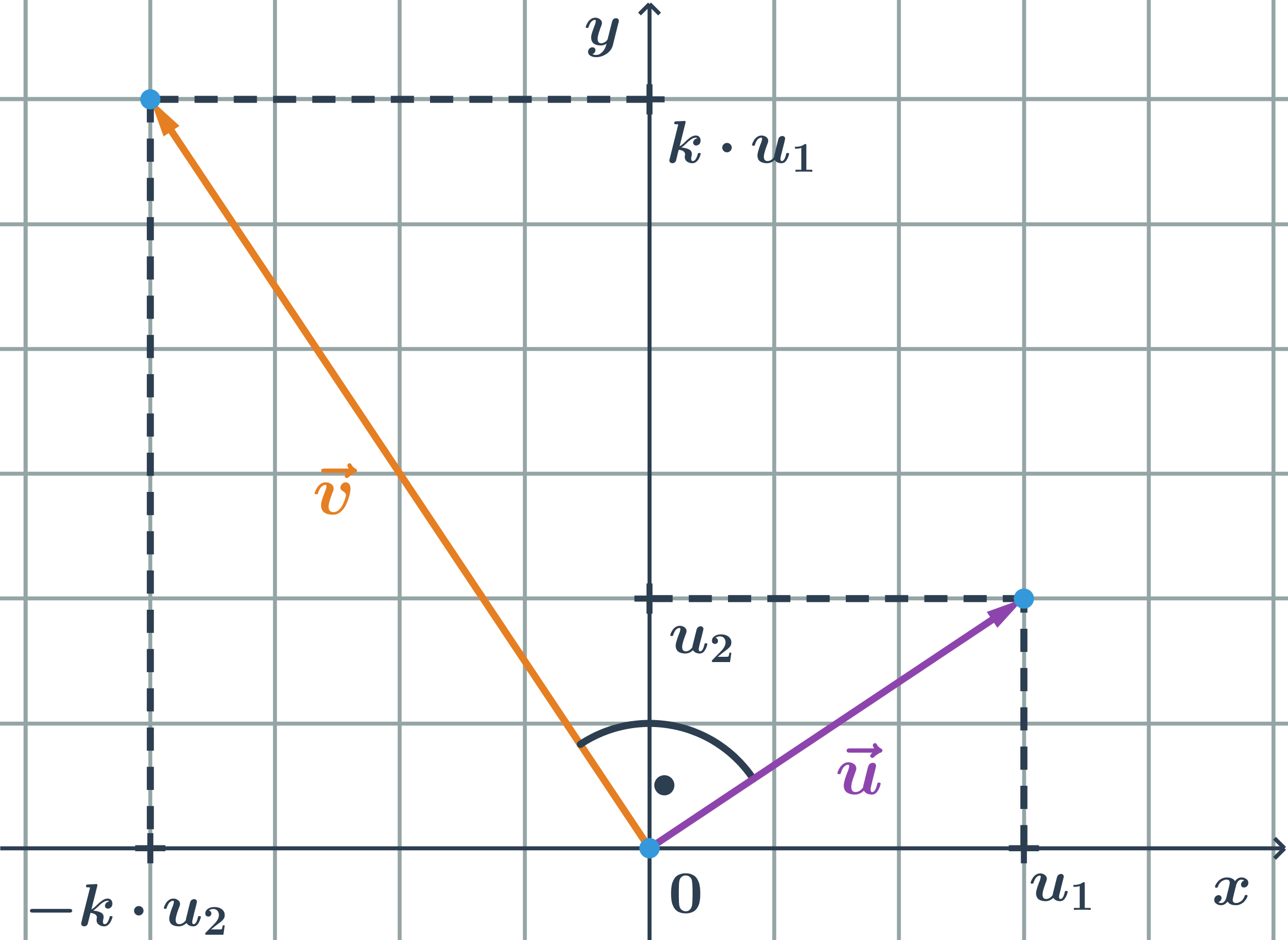
Príklad kolmý vektor
- Doplňte súradnicu vektora \vec{v}=(v_1;4) tak, aby bol kolmý k vektoru \vec{u}=(2;-1).
- Platí: v_2=2 \cdot u_1, teda musí platiť: v_1 = - 2 \cdot u_2.
- Máme teda v_1 = - 2 \cdot u_2 = -2 \cdot (-1) = 2.
Vzájomná poloha vektorov (stredné)
