
Všeobecná rovnica priamky v rovine

Všeobecná rovnica priamky v rovine má tvar: ax+by+c=0, kde konštanty a a b sú súradnice normálového vektora a c reálne číslo. Normálový vektor \vec{n}=(a;b) je vektor kolmý na danú priamku, teda aj kolmý na smerový vektor priamky.
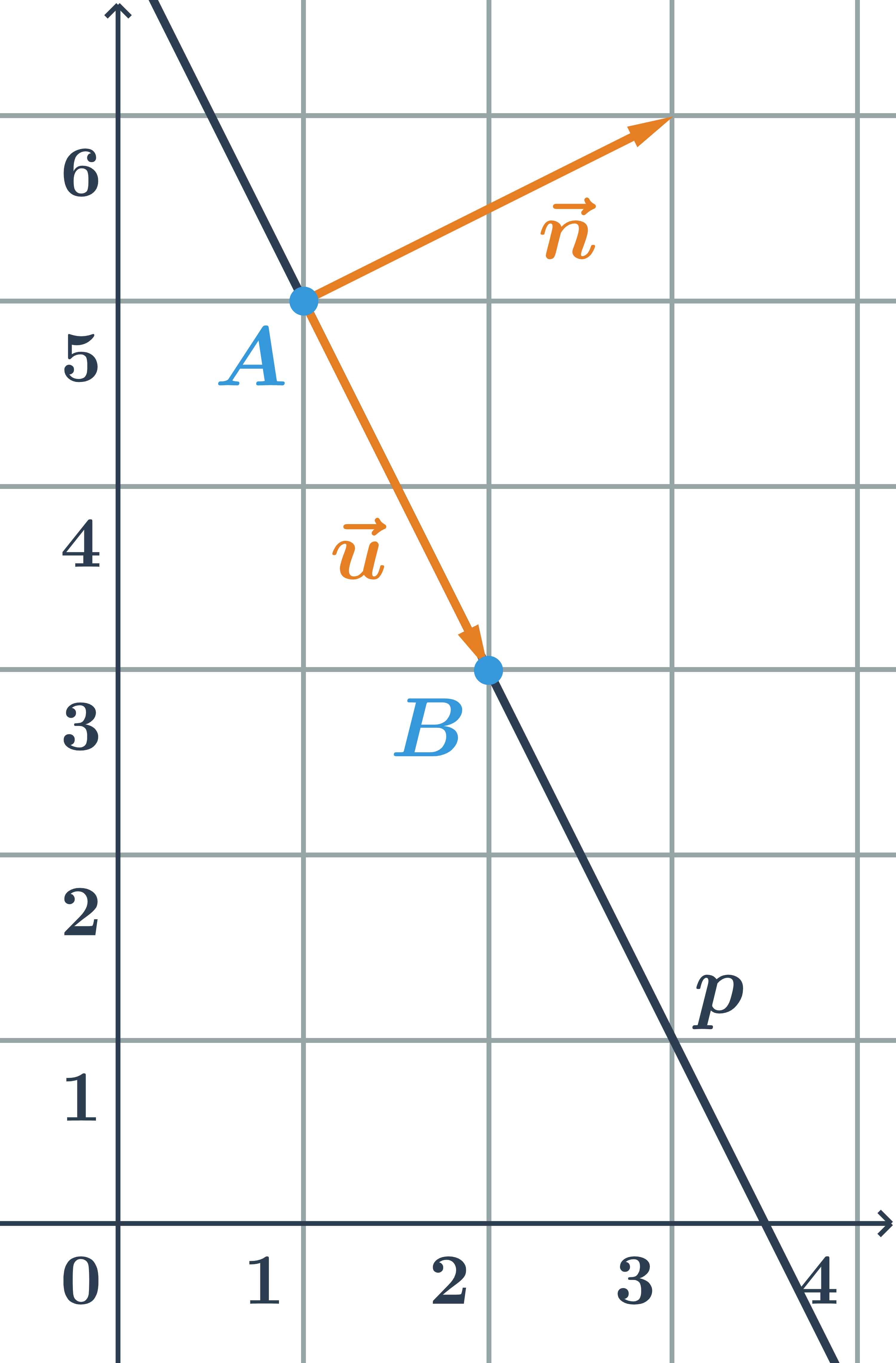
Všeobecná rovnica priamky p určené body A=[1;5] a B=[2;3]
- Priamka p je určená bodom A a smerovým vektorom \vec{u}=\overrightarrow{AB}=B-A=(1;-2).
- Normálový vektor je kolmý na vektor \vec{u}=(1;-2), teda napríklad vektor \vec{n}=(2;1).
- Súradnice normálového vektoru sú konštanty a a b vo všeobecnej rovnici priamky. Všeobecná rovnica má tvar: 2x+y+c=0
- Konštantu c dopočítame dosadením súradníc bodu A=[1;5] :
- 2\cdot1+5+c=0\Rightarrow c=-7
- Všeobecná rovnica priamky p je: 2x+y-7=0
Všeobecná rovnica priamky danej parametricky
Určite všeobecnú rovnicu priamky p, ktorá je daná nasledujúcou parametrickou sústavou rovníc: \begin{array}{rrl}x&=&1+2t\\y&=&4+6t\\&&t\in\mathbb{R}\end{array}
- Priamka p je určená bodom A=[1;4] a smerovým vektorom \vec{u}=(2;6).
- Súradnice smerového vektora môžeme upraviť na tvar: \vec{u}=(1;3).
- Normálový vektor je kolmý na vektor \vec{u}=(1;3), teda napríklad vektor \vec{n}=(3;-1).
- Súradnice normálového vektora sú konštanty a a b vo všeobecnej rovnici priamky. Všeobecná rovnica má tvar: 3x-y+c=0
- Konštantu c dopočítame dosadením súradníc bodu A=[1;4] :
- 3\cdot1-4+c=0\Rightarrow c=1
- Všeobecná rovnica priamky p je: 3x-y+1=0
Parametrické vyjadrenie priamky danej všeobecnou rovnicou
Určite parametrické vyjadrenie priamky p, ktorá má všeobecnú rovnicu: 3x-2y+4=0.
- Priamka p má normálový vektor \vec{n}=(3;-2).
- Smerový vektor je kolmý na vektor \vec{n}=(3;-2), teda napríklad vektor \vec{u}=(2;3).
- Určíme jeden bod na priamke p : jednu súradnicu môžeme zvoliť, napríklad x=0, druhú súradnicu dopočítame: 3\cdot0-2y+4=0\Rightarrow y=2
- Zo všeobecnej rovnice sme teda zistili, že na priamke leží bod A=[0;2].
- Parametrické vyjadrenie priamky p je: \begin{array}{rrl}x&=&0+3t\\y&=&2-2t\\&&t\in\mathbb{R}\end{array}
Zatvoriť












