Grafy kvadratických funkcií

Kvadratickú funkciu je možné vyjadriť v tvare f(x) = ax^2 + bx + c, kde a\neq 0. Grafom kvadratickej funkcie je parabola. Tento graf zobrazuje funkciu 0{,}5 x^2 + x - 4:

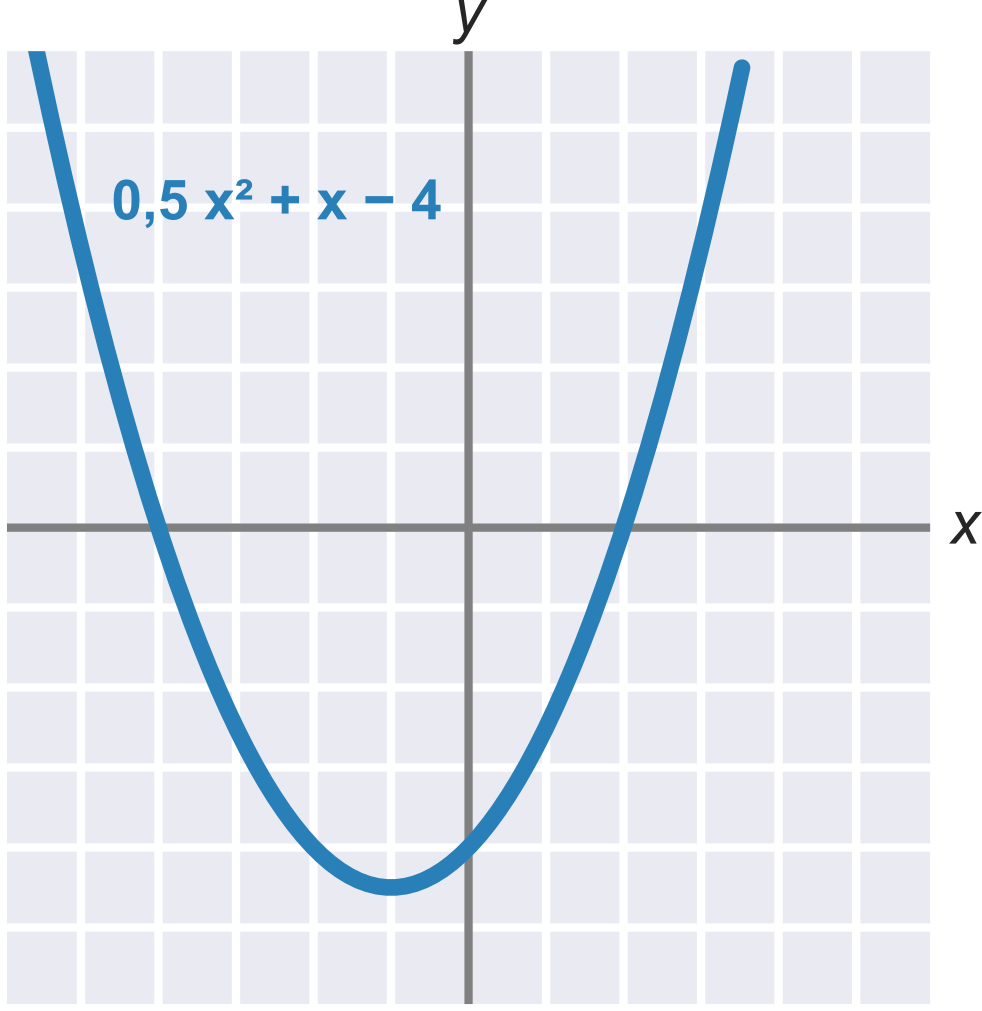
Priesečníky s osou x sú riešenia kvadratickej rovnice ax^2 + bx + c = 0. Pre vyššie uvedený príklad 0{,}5 x^2 + x - 4 sú týmito riešeniami x_1 = -4 a x_2 = 2.

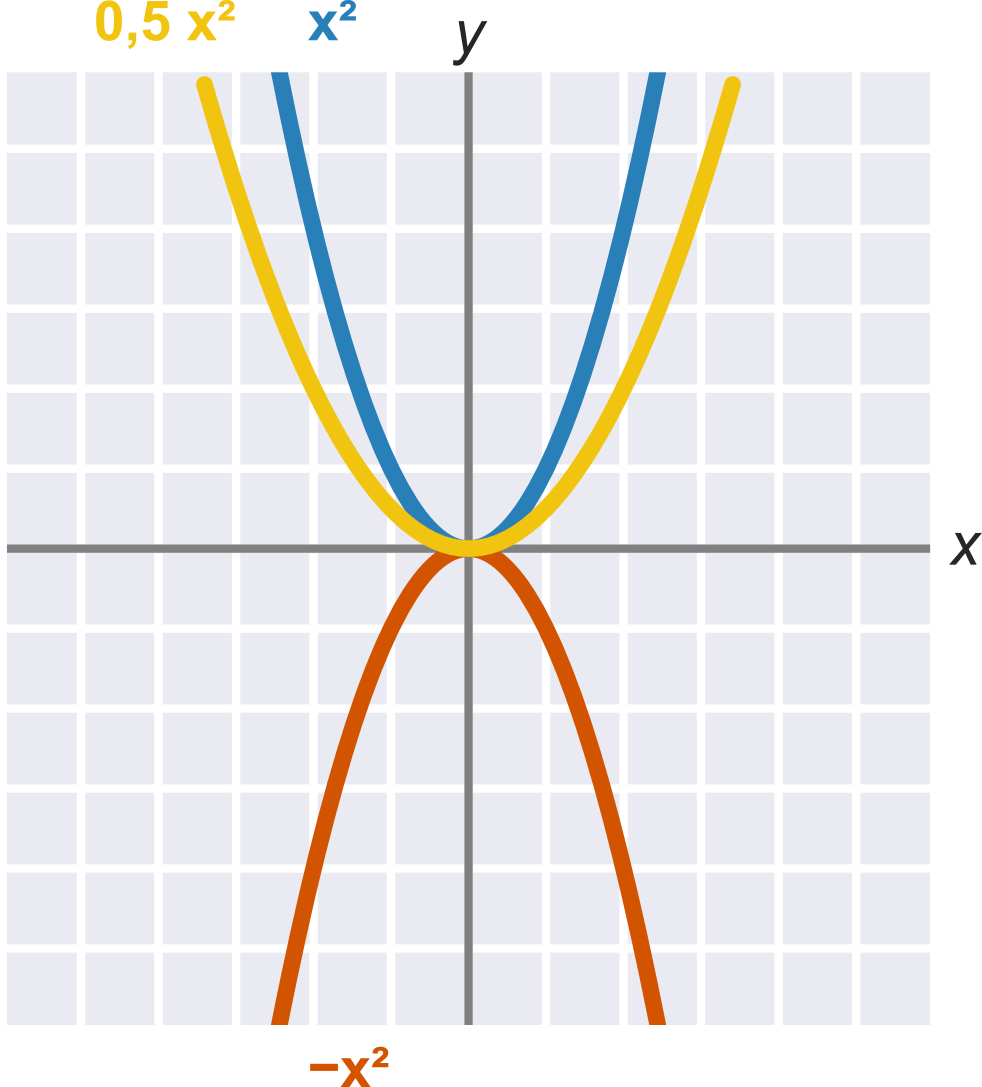
Kvadratický koeficient a ovplyvňuje základnú podobu paraboly:

• Ak je a > 0, „smeruje parabola hore“ (presnejšie: je to zdola obmedzená, konvexná funkcia).
• Ak je a \lt 0, „smeruje parabola dole“ (presnejšie: je to zhora obmedzená, konkávna funkcia).
• Veľkosť kvadratického koeficientu a ovplyvňuje, ako je parabola „široká“.

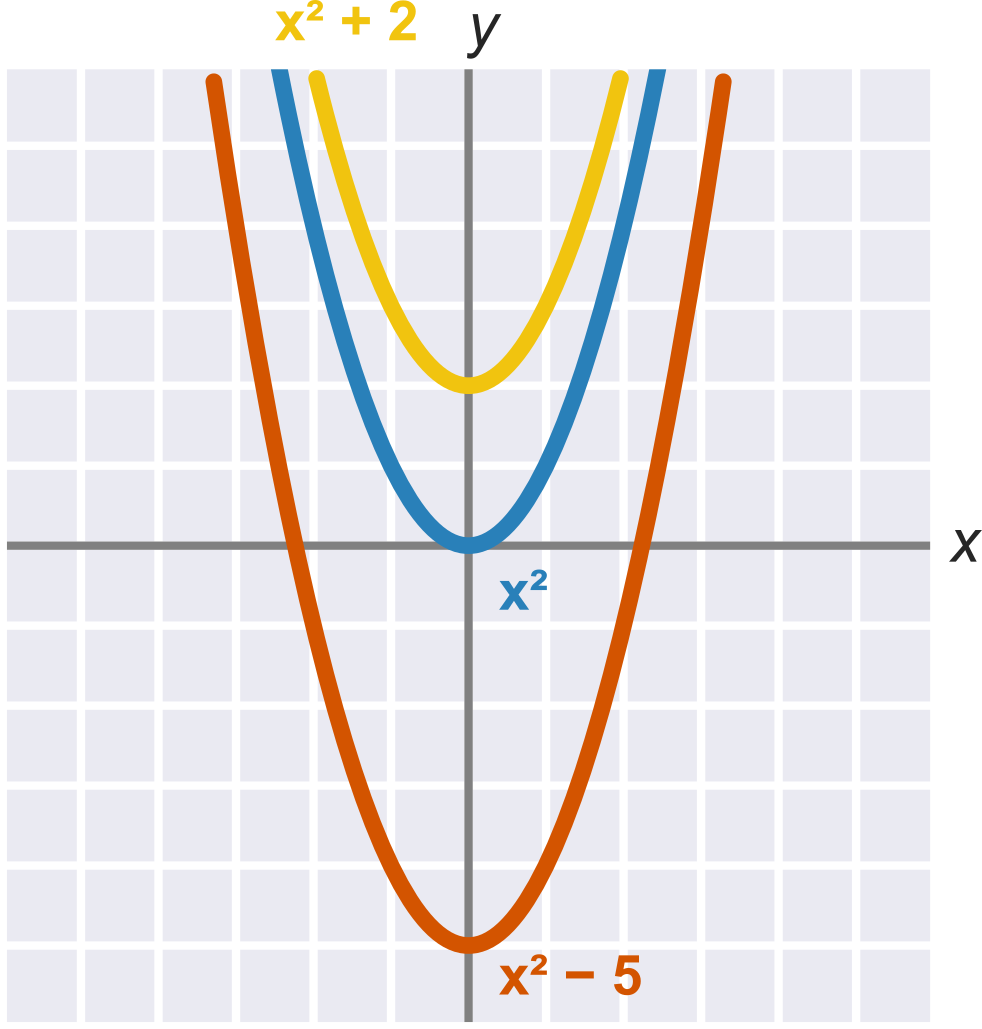
Konštantný člen c ovplyvňuje posun paraboly – udáva priesečník s osou y.