Výpis prehľadov
Logaritmus
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Logaritmus
Logaritmus je inverzná operácia k umocňovaniu. Logaritmus kladného čísla x pri základe a je také reálne číslo y = \log_a(x), pre ktoré platí a^y = x. Číslo a sa nazýva základ logaritmu (báza).
Logaritmus so základom e=2{,}71 828 182... (Eulerovo číslo) sa nazýva prirodzený logaritmus a značí sa väčšinou \ln.
Logaritmus so základom 10 sa nazýva dekadický logaritmus (a niekedy sa značí \mathit{lg}).
Logaritmy majú veľmi široké využitie v mnohých oblastiach matematiky. Historicky sa využívali ako užitočná počítacia pomôcka („logaritmické pravítko“), ktorá využívala fakt, že logaritmus súčinu je súčet logaritmov. Dnes na logaritmy často narazíme napríklad v informatike pri návrhu a analýze algoritmov.
Vlastnosti logaritmov:
- Logaritmus je definovaný len pre kladné čísla.
- Logaritmus so základom 1 nie je definovaný.
- Logaritmus jednotky je nula, \log_a(1)=0.
- Logaritmus s rovnakým základom a argumentom je 1, \log_a{a}=1.
- Logaritmus súčinu je súčet logaritmov, \log_a(x\cdot y)=\log_a{x}+\log_a{y}.
- Logaritmus podielu je rozdiel logaritmov, \log_a\left(\frac{x}{y}\right)=\log_a{x}-\log_a{y}.
- Logaritmus je inverzná funkcia k exponenciálnej funkcii s rovnakým základom, \log_a{x}=y \Leftrightarrow a^y=x.
- Logaritmus mocniny je súčin exponentu a logaritmu základu mocniny, \log_a(x^n)=n\log_a{x}.
Graf logaritmu so základom 2:
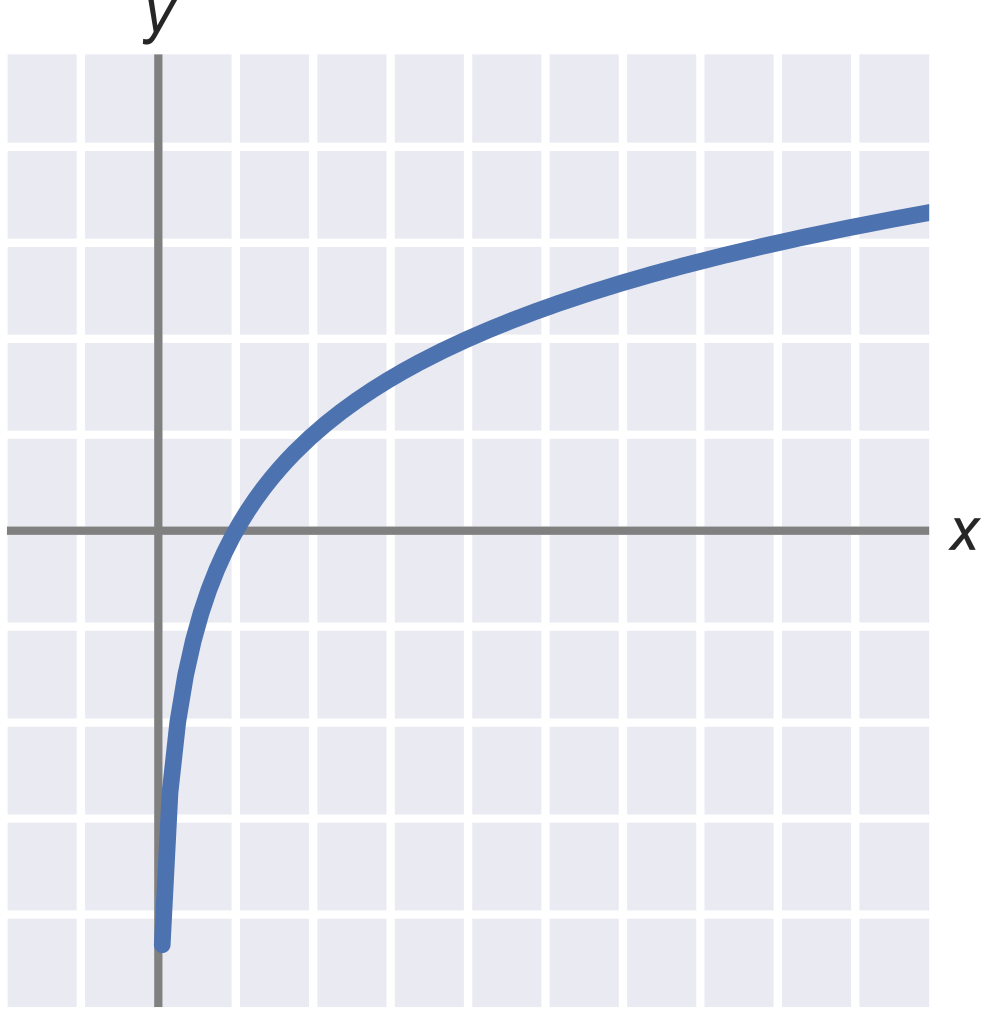
Logaritmus: výpočet
Logaritmus kladného čísla x pri základe a je také reálne číslo y = \log_a(x), pre ktoré platí a^y = x. Príklady:
| \log_{10}(100) = 2 | pretože 10^2 = 100 |
| \log_2(32) = 5 | pretože 2^5 = 32 |
| \log_5(125) = 3 | pretože 5^3 = 125 |
| \log_7(1) = 0 | pretože 7^0 = 1 |
| \log_2(0{,}5) = -1 | pretože 2^{-1} = \frac{1}{2} = 0{,}5 |
Výrazy s logaritmami
Niektoré základné vlastnosti logaritmov vyjadrené pomocou vzorcov:
- \log_a(a)=1
- \log_a(1)=0
- \log_a(x\cdot y) = \log_a(x) + \log_a(y) (logaritmus súčinu je súčet logaritmov)
- \log_a(\frac{x}{y}) = \log_a(x) - \log_a(y) (logaritmus podielu je rozdiel logaritmov)
- \log_a(x^k)=k\log_a(x)
- \log_a(x)=\frac{\log_b(x)}{\log_b(a)}


 Slovenčina
Slovenčina Angličtina
Angličtina Informatika
Informatika Vieme to
Vieme to Nemčina
Nemčina Biológia
Biológia Zemepis
Zemepis Chémia
Chémia Fyzika
Fyzika