Slovenčina
Angličtina
Informatika
Vieme to
Nemčina
Biológia
Zemepis
Chémia
Fyzika
Aritmetika
Zlomky, percentá, desatinné čísla
Geometria
Elementárna algebra
Funkcie
Jednotky, miery
Diskrétna matematika
Finančná gramotnosť
Rozhodovačka
Pexeso
Krok za krokom
Počítanie
Grafár
Porozumenie
Označovanie
Presúvanie
Mriežkovaná
Rozdeľovačka
Pokazená kalkulačka
Roboti
Strieľačka
Príšerky
Preteky
Územia
Tipovačka
Tímovka
Môj účet
Odhlásiť saVýpis prehľadov
Metrické úlohy
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Metrické úlohy
V metrických úlohách v analytickej geometrii býva úlohou vypočítať konkrétnu číselnú hodnotu veličín ako je:
- vzdialenosť dvoch objektov, napr. vzdialenosť bodu od priamky,
- odchýlka dvoch priamok v rovine.
Vzdialenosť bodu od priamky
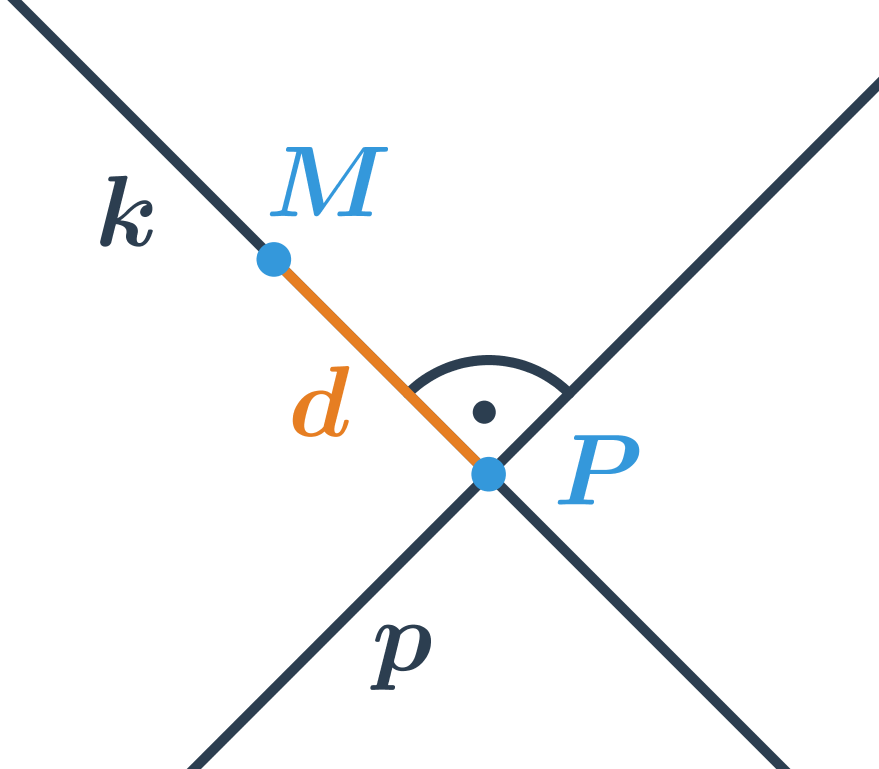
Vzdialenosť bodu od priamky je dĺžka najkratšej úsečky určenej bodom M a bodom ležiacim na priamke p. Ako je vidieť z obrázka, táto najkratšia úsečka leží na kolmici z bodu M k priamke p. Vzdialenosť bodu od priamky teda môžeme určiť takto:
- nájdeme priamku k, ktorá prechádza bodom M a je kolmá na priamku p
- určíme priesečník P priamky k s priamkou p
- vzdialenosť bodu M od priamky p je dĺžka úsečky PM
Príklad: vzdialenosť bodu od priamky – pomocou kolmice
Určite vzdialenosť bodu M=[5;2] od priamky p:4x+3y-1=0.
- Priamka k, ktorá prechádza bodom M a je kolmá na priamku p má smerový vektor kolineárny s normálovým vektorom priamky p.
- Súradnice smerového vektora priamky k sú: \vec{u}=(4;3).
- Priamka k má parametrické vyjadrenie: p:X=M+t\vec{u}
- p:\begin{array}{rrl}x&=&5+4t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
- Súradnice priesečníka P priamky k s priamkou p určíme dosadením parametrického vyjadrenia priamky k do všeobecnej rovnice priamky p.
\begin{array}{rrl}4(5+4t)+3(2+3t)-1&=&0\\20+16t+6+9t-1&=&0\\25+25t&=&0\Rightarrow t=-1\end{array}
- Priesečník priamok k a p je bod P=[1;-1].
- Vzdialenosť bodu M od priamky p je dĺžka úsečky PM:
- Vzorec pre dĺžku úsečky: d=\sqrt{(x_M-x_P)^2+(y_M-y_P)^2}
- Dosadíme súradnice bodov M,P: d=\sqrt{(5-1)^2+(2-(-1))^2}=\sqrt{16+9}=5
Vzorec pre vzdialenosť bodu od priamky danej všeobecnou rovnicou
Vzdialenosť bodu M=[m_1;m_2] od priamky p danej všeobecnou rovnicou ax+by+c=0 je daná vzorcom: d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}}
Príklad: vzdialenosť bodu od priamky – pomocou vzorca
Určite vzdialenosť bodu M=[5;2] od priamky p:4x+3y-1=0 s využitím vzorca.
- Dosadíme do vzorca d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} súradnice bodu M=[5;2] a koeficienty a a b zo všeobecnej rovnice priamky.
- Všeobecná rovnica pre p je 4x+3y-1=0, teda a=4 a b=3.
- Máme: d=\frac{\left| 4\cdot5+3\cdot2-1\right|}{\sqrt{4^2+3^2}}=\frac{25}{\sqrt{25}}=5
Vzdialenosť dvoch rovnobežiek
Ak vieme určiť vzdialenosť bodu od priamky, ľahko určíme tiež vzdialenosť dvoch rovnobežiek. Stačí si uvedomiť, že všetky body ležiace na jednej priamke majú od druhej priamky rovnakú vzdialenosť. Preto je vzdialenosť rovnobežiek rovnaká ako vzdialenosť ľubovoľného bodu na jednej priamke od priamky druhej.
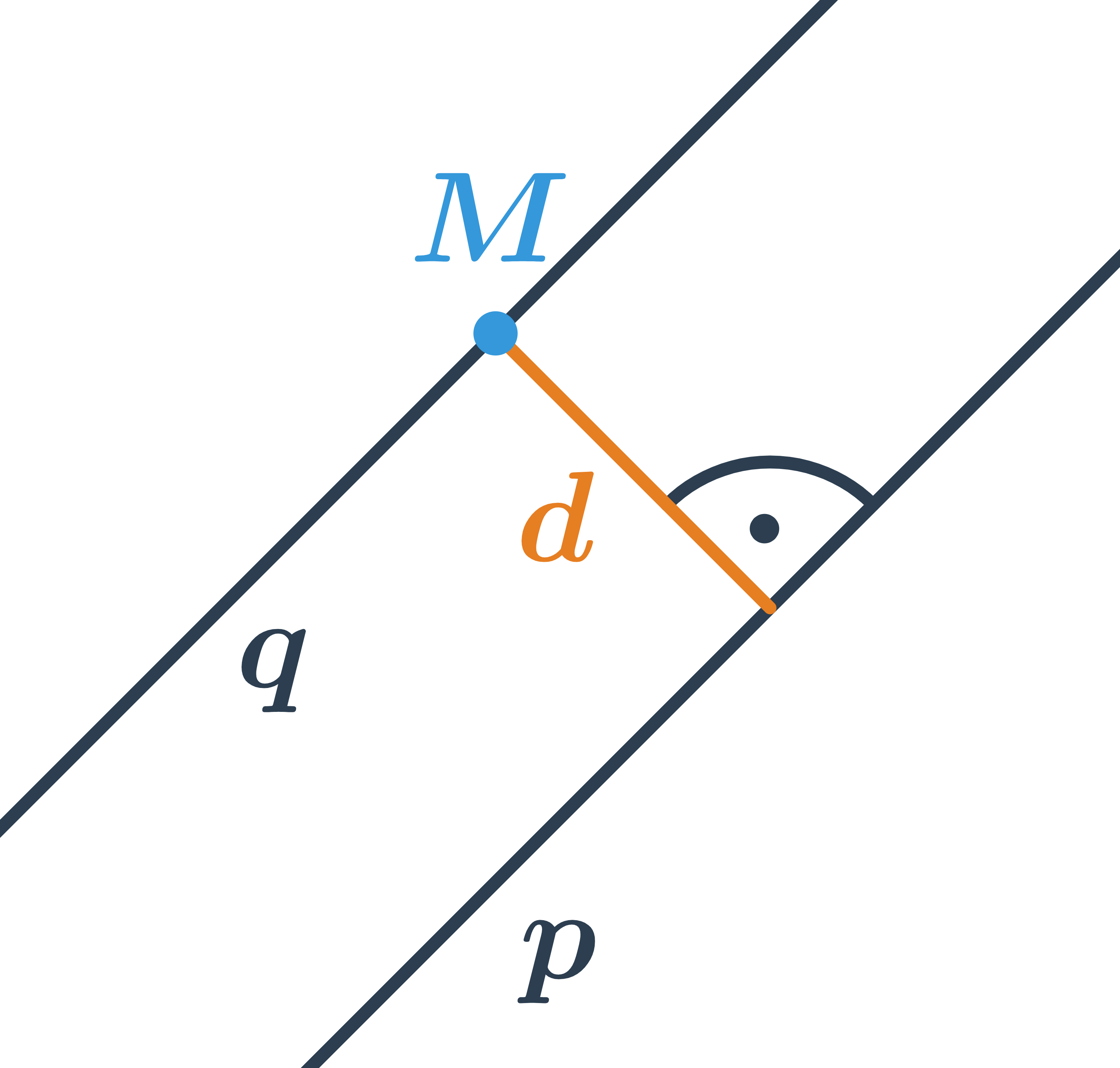
Príklad: vzdialenosť rovnobežiek
Určite vzdialenosť rovnobežiek p:2x-4y+3=0 a q:x-2y+1=0.
- Určíme súradnice jedného bodu (M) na priamke q tak, že jednu súradnicu zvolíme a druhú dopočítame.
- Zvolíme napríklad súradnicu y=0, potom x-2\cdot0+1=0\Rightarrow x=-1
- Dosadíme do vzorca d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} súradnice bodu M=[-1;0] a koeficienty a a b zo všeobecnej rovnice priamky p.
- Všeobecná rovnica pre p je 2x-4y+3=0, teda a=2 a b=-4.
- Máme: d=\frac{\left| 2\cdot(-1)-4\cdot0+3\right|}{\sqrt{2^2+(-4)^2}}=\frac{1}{\sqrt{20}}
- Vzdialenosť rovnobežiek p a q je: d=\frac{1}{\sqrt{20}}
Odchýlka dvoch priamok
Odchýlka rovnobežiek je 0^\circ. Odchýlka rôznobežiek je veľkosť ostrého alebo pravého uhla, ktorý priamky zvierajú.
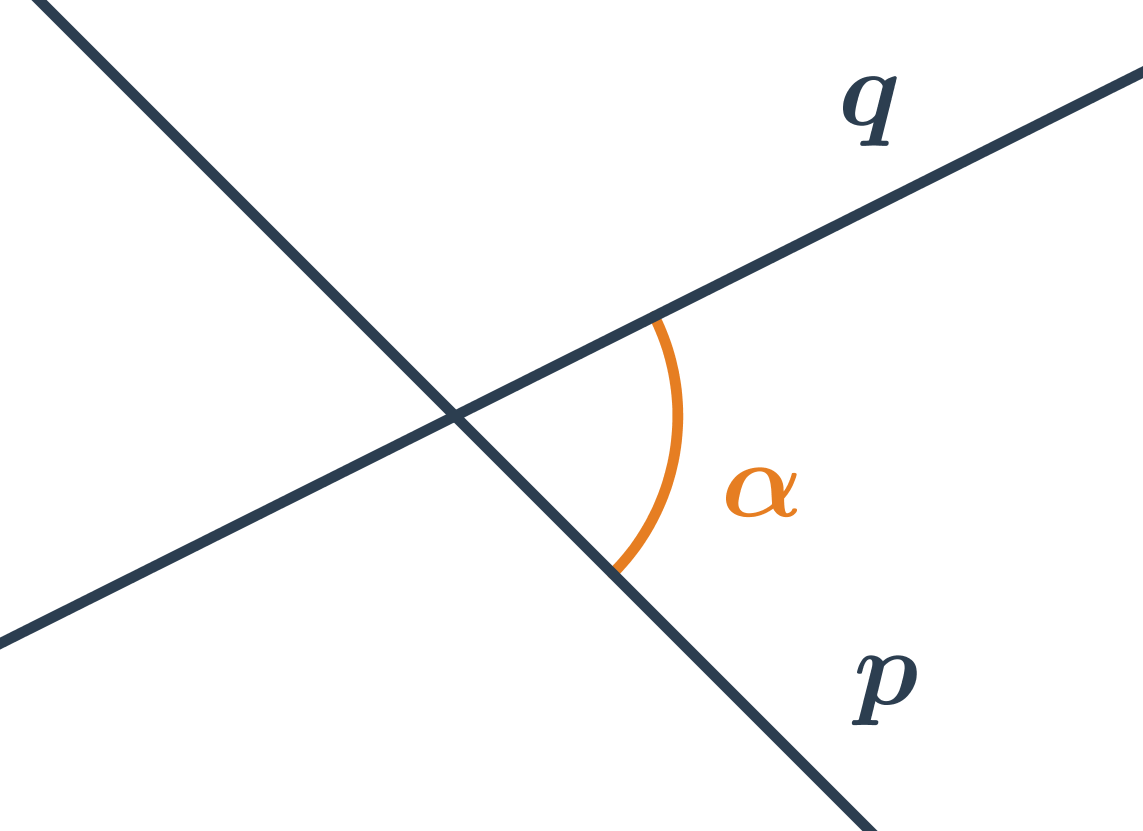
Odchýlku rôznobežiek p a q môžeme vypočítať na základe znalosti smerových alebo normálových vektorov priamok. Vzorec na výpočet uhlov rôznobežiek je podobný ako vzorec na výpočet uhla vektorov.
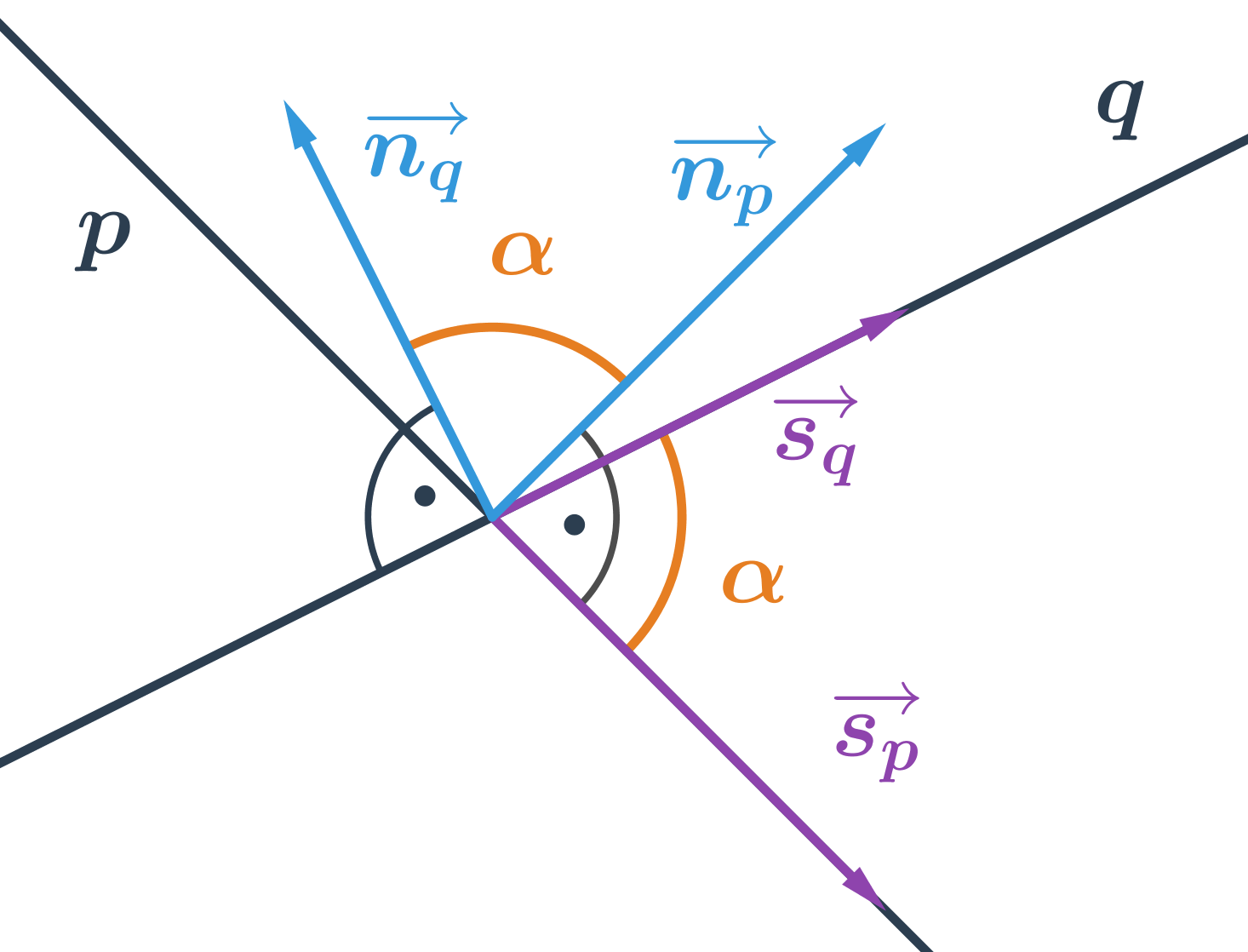
Odchýlka rôznobežiek je uhol \alpha, pre ktorý platí: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|} Vektory \vec{u} a \vec{v} uvedené vo vzorci sú smerové vektory \overrightarrow{s_p} a \overrightarrow{s_q} alebo normálové vektory \overrightarrow{n_p} a \overrightarrow{n_q} priamok p a q.
Pre dve na seba kolmé priamky platí, že ich odchýlka \alpha=90^\circ a teda \cos\alpha=0.
Prečo musí byť vo vzorci pre výpočet odchýlky priamok absolútna hodnota?
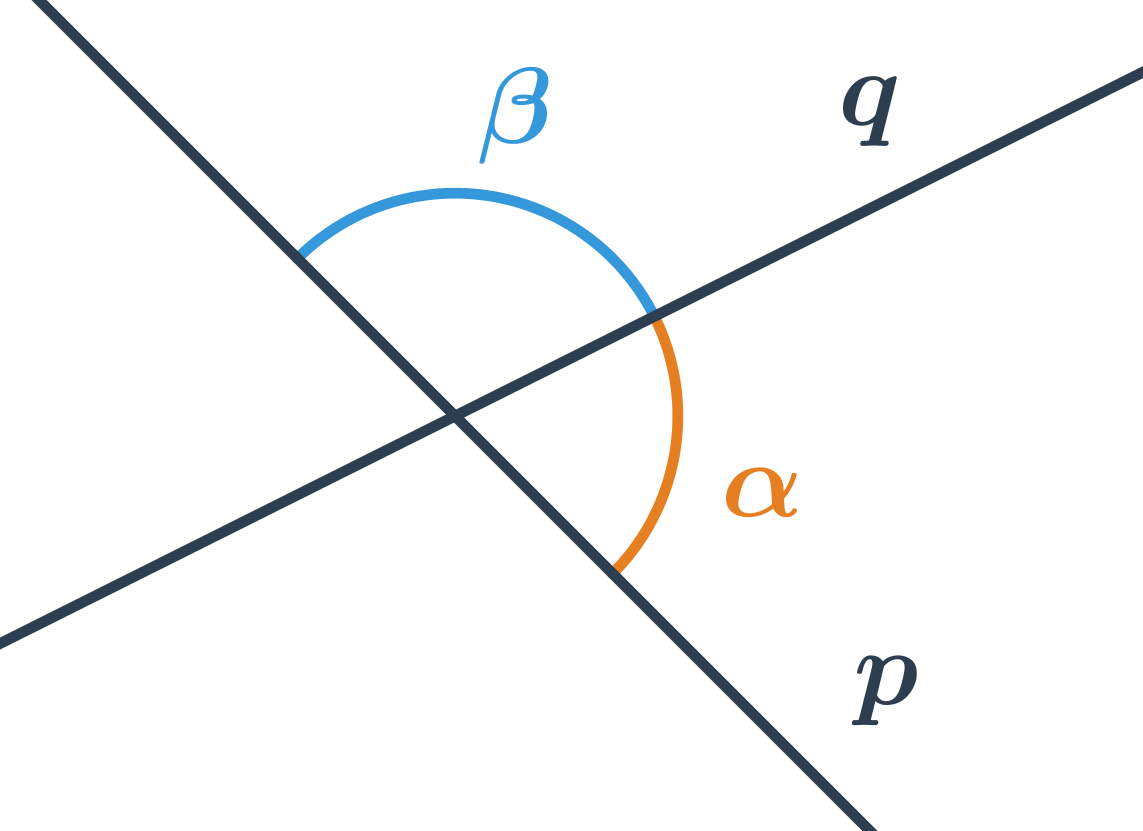
- Odchýlka priamok p a q na obrázku je ostrý uhol \alpha, nie tupý uhol \beta.
- \alpha a \beta sú vedľajšie uhly, pre ktoré je hodnota funkcie \cos opačná, teda: \cos\alpha=-\cos\beta
- Pre uhol \alpha je \cos\alpha > 0, pre \beta je \cos\beta < 0
- Absolútna hodnota vo vzorci nám zaručí, že nájdeme uhol, kde hodnota funkcie \cos je kladná, teda uhol ostrý, ktorý je odchýlkou daných priamok.
Odchýlka priamok a uhly v trojuholníku
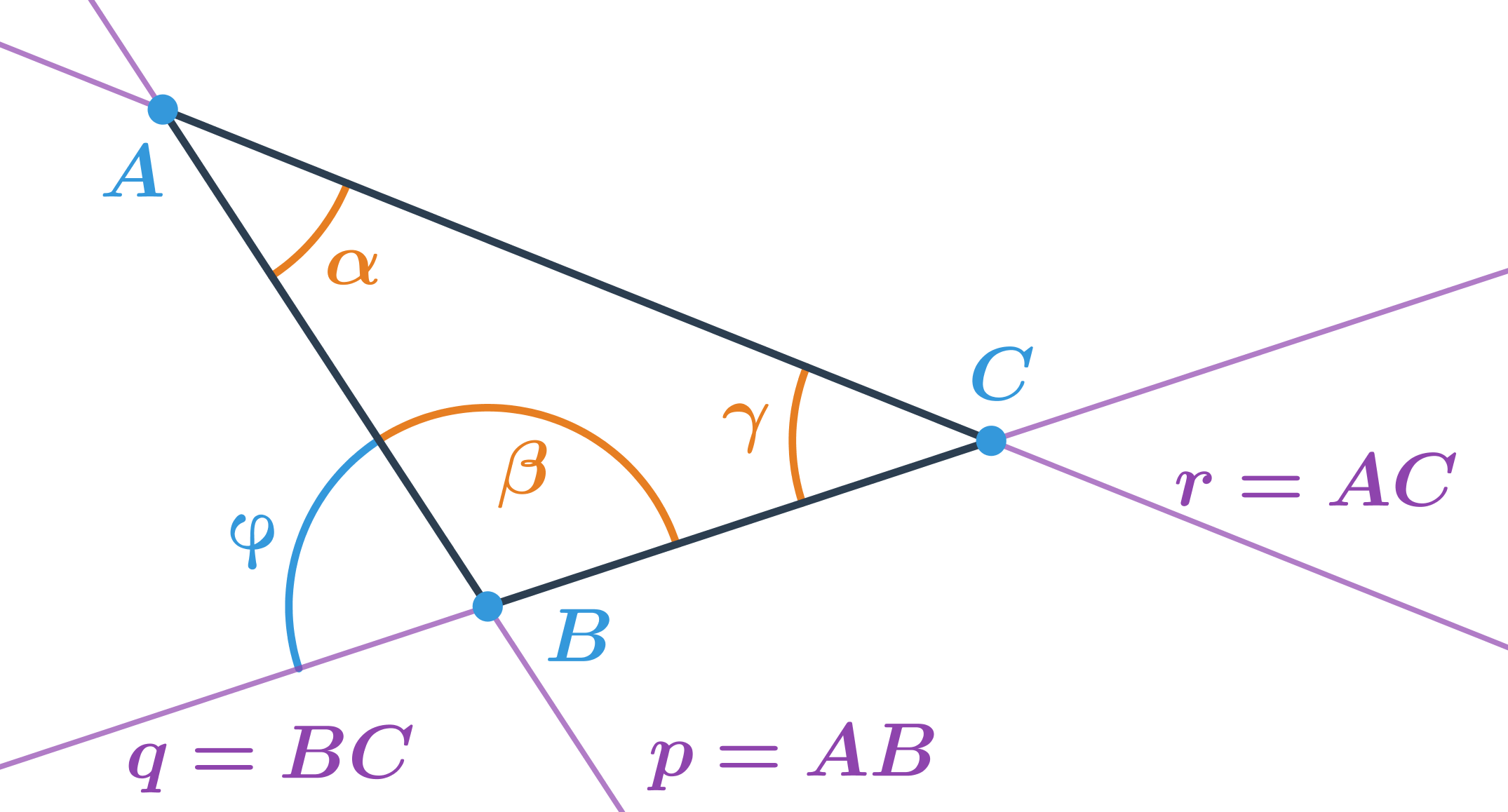
V trojuholníku na obrázku:
- uhol \alpha je menší než 90^\circ a je to odchýlka priamok AB a AC
- uhol \beta je väčší než 90^\circ a nie je to odchýlka priamok AB a BC
- uhol \gamma je menší než 90^\circ a je to odchýlka priamok BC a AC
Veľkosť uhlov v trojuholníku nemusí byť rovnaká ako odchýlka priamok, na ktorých ležia strany trojuholníka. Uhly v trojuholníku počítame ako odchýlku vektorov, ktoré určujú daný uhol. Tento uhol môže byť väčší než 90^\circ, preto využijeme vzorec pre výpočet odchýlky vektorov (vo vzorci nebude absolútna hodnota).
Odchýlka priamok
Určite odchýlku priamok p:x-2y+3=0 a q:2x-y+1=0
- Priamky sú dané všeobecnými rovnicami, preto pre výpočet ich odchýlky využijeme normálové vektory: \overrightarrow{n_p}=(1;-2) a \overrightarrow{n_q}=(2;-1)
- Dosadíme do vzorca: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|}=\frac{\left| 1\cdot2+(-2) \cdot(-1) \right|}{\sqrt{1^2+(-2)^2}\cdot\sqrt{2^2+(-1)^2}}=\frac{4}{\sqrt{5}\cdot \sqrt{5}}=\frac{4}{5}
- Pomocou funkcie cos^{-1} na kalkulačke dopočítame odchýlku: \alpha=36^\circ
