Výpis prehľadov
Operácie a vlastnosti v rovine
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Operácie a vlastnosti v rovine
Základná intuitívna predstava pre jednotlivé operácie a vlastnosti:
- Osová súmernosť: robíme „zrkadlový“ obraz útvaru podľa priamky.
- Stredová súmernosť: preklápame útvar podľa bodu.
- Rotácia: otočíme útvar okolo určitého bodu o nejaký uhol.
- Zhodnosť: dva útvary sú zhodné, ak „majú rovnaký tvar a veľkosť“ (môžu sa líšiť natočením a umiestnením).
- Podobnosť: dva útvary sú podobné, ak „majú rovnaký tvar“ (môžu sa líšiť veľkosťou, natočením a umiestením).
Téma určenie zobrazení v rovine sa potom zaoberá rozlišovaním medzi jednotlivými zobrazeniami.
HoreOsová súmernosť
Osová súmernosť je daná priamkou o a priraďuje každému bodu X mimo os taký bod X', že priamka o je osou úsečky XX'. Inými slovami: obraz má od osi rovnakú vzdialenosť ako pôvodný bod a spojnica bodov je kolmá na os. Osová súmernosť zachováva vzdialenosti aj uhly, ide teda o druh zhodnosti.
Príklady
Modré a oranžové útvary sú vzájomne osovo súmerné podľa osi o:
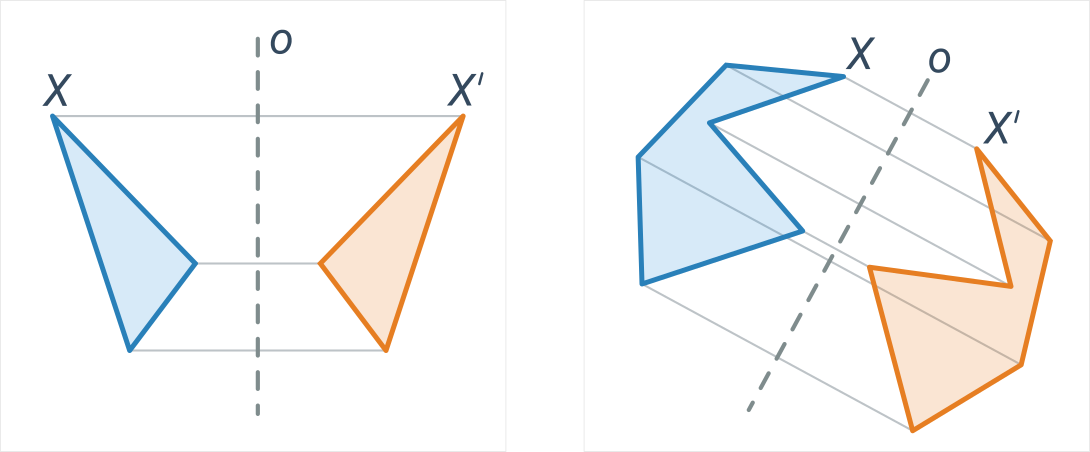
Pre lepšie pochopenie môže byť užitočné porovnať osovú a stredovú súmernosť.
Osovo súmerný útvar
Útvar označujeme za osovo súmerný, ak je v nejakej osovej súmernosti obrazom seba samého. Os tejto súmernosti potom nazývame osou útvaru. Obrázok uvádza príklady útvarov osovo súmerných (zelené, s vyznačenými osami súmernosti) aj tých nesúmerných (červené):
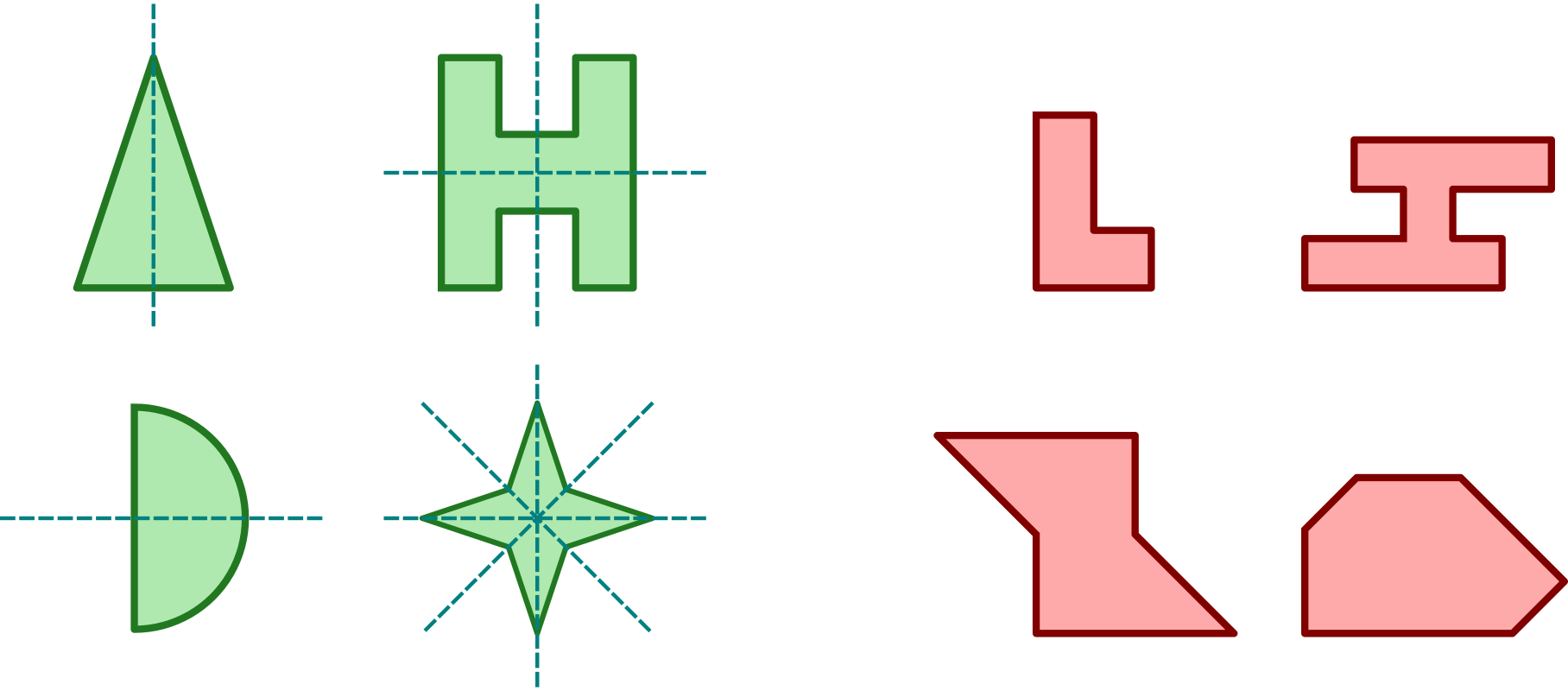
Ďalšie príklady:
- Úsečka je osovo súmerná a má v rovine jedinú os súmernosti (kolmicu v jej strede).
- Rovnoramenný trojuholník je osovo súmerný.
- Trojuholník, ktorý nie je rovnoramenný, nie je osovo súmerný.
- Všetky pravidelné mnohouholníky sú osovo súmerné. Počet osí súmernosti je rovný počtu vrcholov mnohouholníka.
- Kruh je osovo súmerný a má nekonečne veľa osí súmernosti.
Stredová súmernosť
Stredová súmernosť je daná bodom S a priraďuje každému bodu X taký bod X', že bod S je stredom úsečky XX'. Inými slovami: obraz má od stredu rovnakú vzdialenosť ako pôvodný bod a leží na polpriamke opačnej k SX.
Stredová súmernosť zachováva vzdialenosti aj uhly, ide teda o druh zhodnosti. Stredová súmernosť so stredom v bode S je zhodná s otočením o 180 stupňov podľa stredu S.
Príklady
Modré a oranžové útvary sú vzájomne stredovo súmerné podľa stredu S:
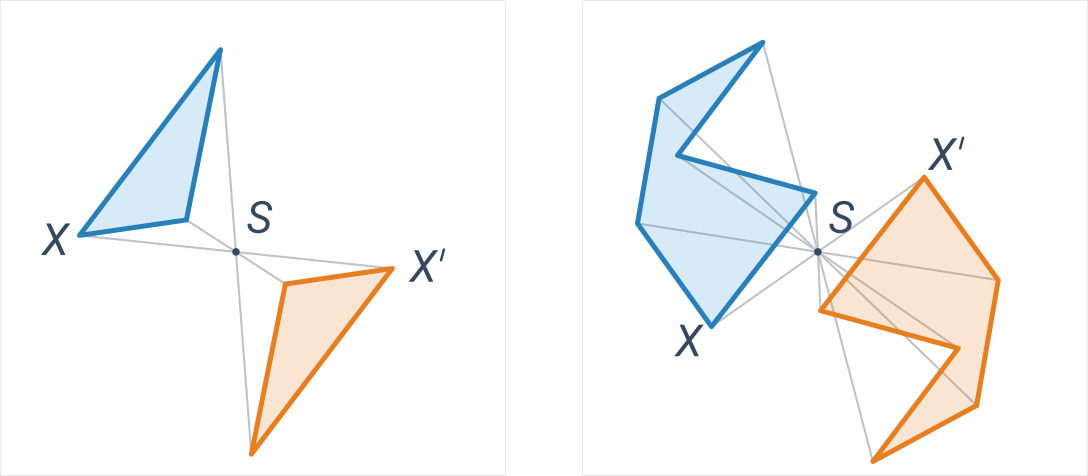
Pre lepšie pochopenie môže byť užitočné porovnať stredovú a osovú súmernosť.
Stredovo súmerný útvar
Útvar označujeme za stredovo súmerný, ak je v nejakej stredovej súmernosti obrazom seba samého. Stred tejto stredovej súmernosti potom nazývame stredom súmernosti objektu. Obrázok uvádza príklady útvarov stredovo súmerných (zelené, s vyznačeným stredom súmernosti) aj tých nesúmerných (červené):
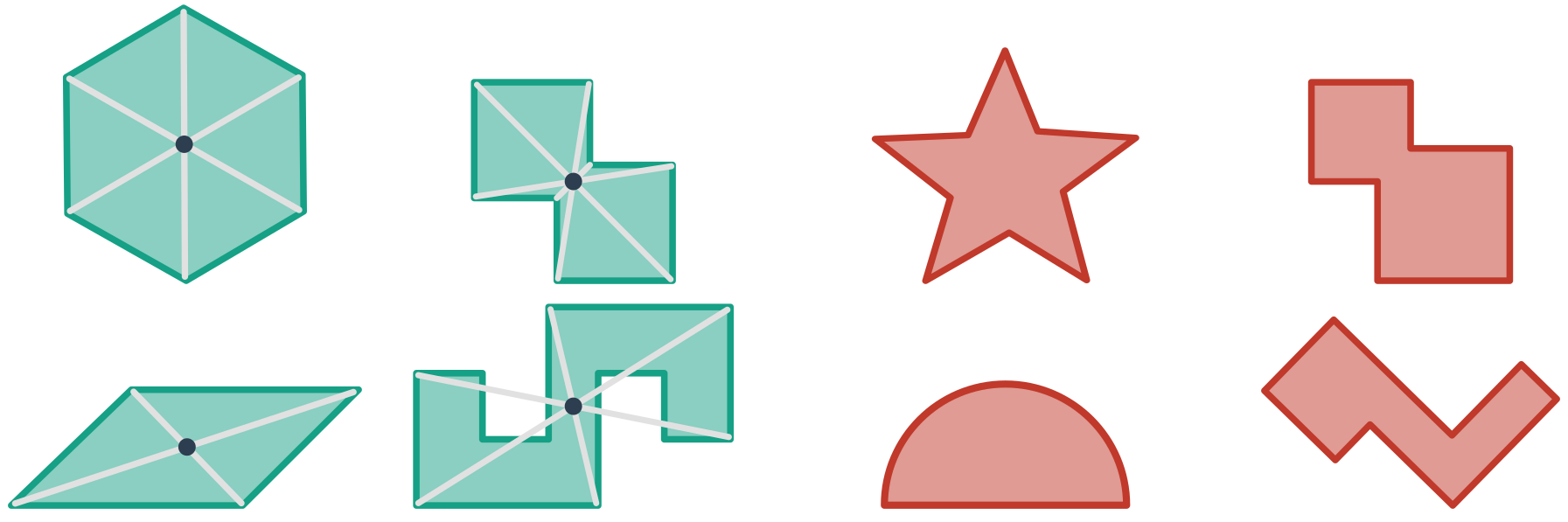
Ďalšie príklady:
Úsečka, obdĺžnik, štvorec, kosoštvorec, pravidelný šesťuholník a kruh sú stredovo súmerné.
Žiadny trojuholník nie je stredovo súmerný.
Dva geometrické útvary sú zhodné, keď majú rovnaký tvar a veľkosť. Na nasledujúcom obrázku majú zhodné útvary rovnakú farbu.

Značenie
Majme dva pomenované útvary, napr. dva trojuholníky ABC a GEF.
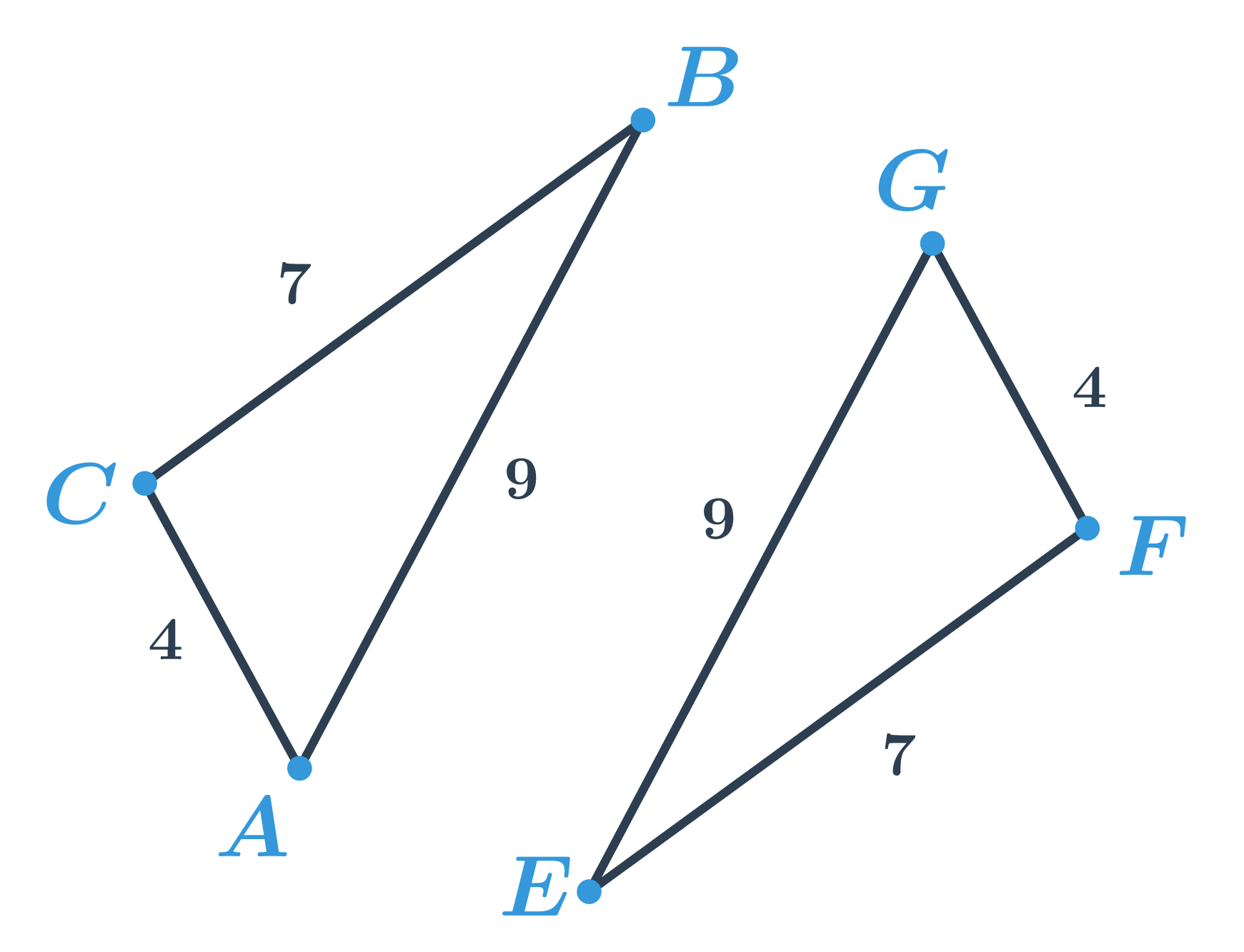
- \left|AB\right|=\left|GE\right|
- \left|BC\right|=\left|EF\right|
- \left|AC\right|=\left|GF\right|
Tieto dva trojuholníky majú rovnaké dĺžky strán, sú teda zhodné. Zapíšeme ako ABC \cong GEF – pozor, na poradí písmen záleží. Poradie písmen v názve trojuholníka určuje, ktorý vrchol ABC zodpovedá ktorému vrcholu trojuholníka GEF. Máme \left|AB\right|=\left|GE\right|, ale \left|AB\right|\neq \left|EF\right|, takže ABC \ncong EFG.
HorePodobnosť
Dva geometrické útvary sú si podobné, ak majú oba rovnaký tvar (bez ohľadu na veľkosť). Na nasledujúcom obrázku majú podobné útvary rovnakú farbu:

Presnejšie povedané, útvary sú podobné, ak jeden môžeme získať z druhého kombináciou rovnomerného zmenšenia alebo zväčšenia a následným posunutím, otočením alebo prevrátením.
Podobnosť zachováva veľkosť uhlov a pomer dĺžok.
Pomer dĺžok zodpovedajúcich úsečiek v oboch útvaroch sa nazýva koeficient podobnosti.
HorePosunutie
Posunutie je dané orientovanou úsečkou. Táto úsečka určuje smer a dĺžku posunutia. Orientovaná úsečka je úsečka, pri ktorej rozlišujeme, ktorý bod je počiatočný a ktorý koncový. Orientovanú úsečku označíme šípkou, ktorá určí jej smer. Zápis \overrightarrow{PQ} znamená, že počiatočným bodom orientovanej úsečky je bod P a koncovým bodom bod Q. Na obrázku sú orientované úsečky \overrightarrow{PQ} a \overrightarrow{NM}. Tieto úsečky majú rovnakú dĺžku, ale opačný smer.
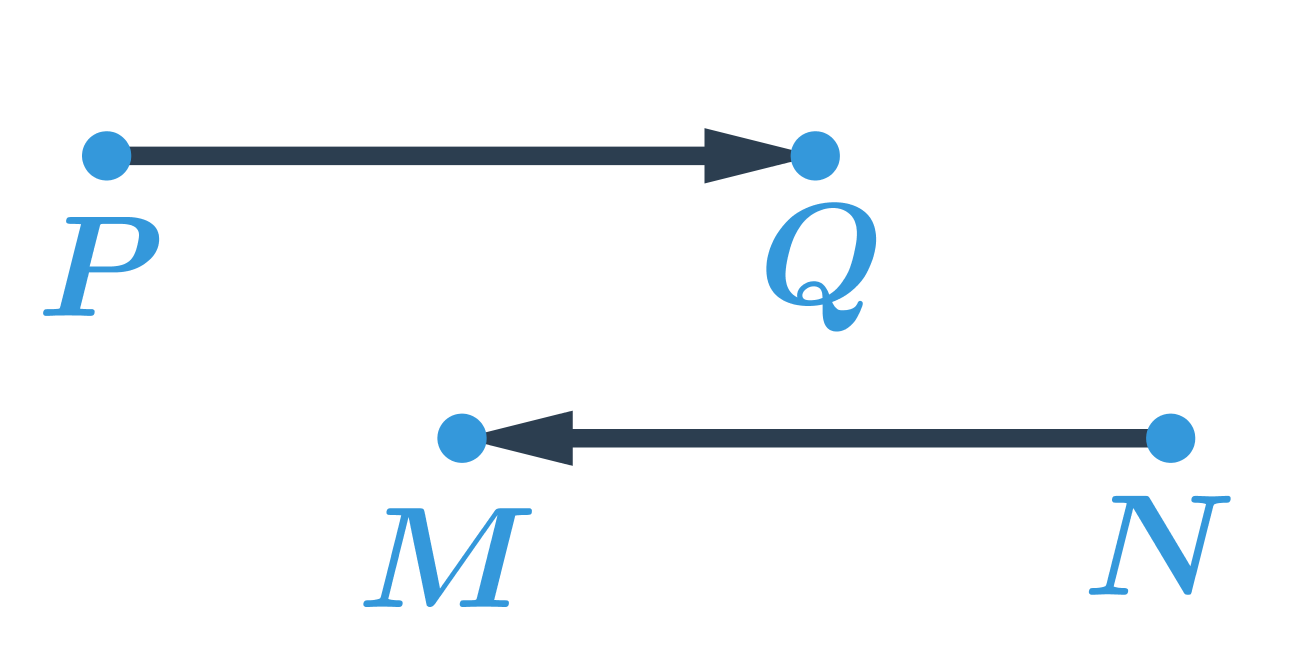
Obrazom bodu X v posunutí, ktoré je určené orientovanou úsečkou \overrightarrow{PQ}, je bod X', pre ktorý platí, že orientovaná úsečka \overrightarrow{XX'} má rovnakú veľkosť a rovnaký smer ako orientovaná úsečka \overrightarrow{PQ}.
Príklad: posunutie bodu
Obrazom bodu X v posunutí, ktoré je určené orientovanou úsečkou \overrightarrow{PQ}, je bod X':
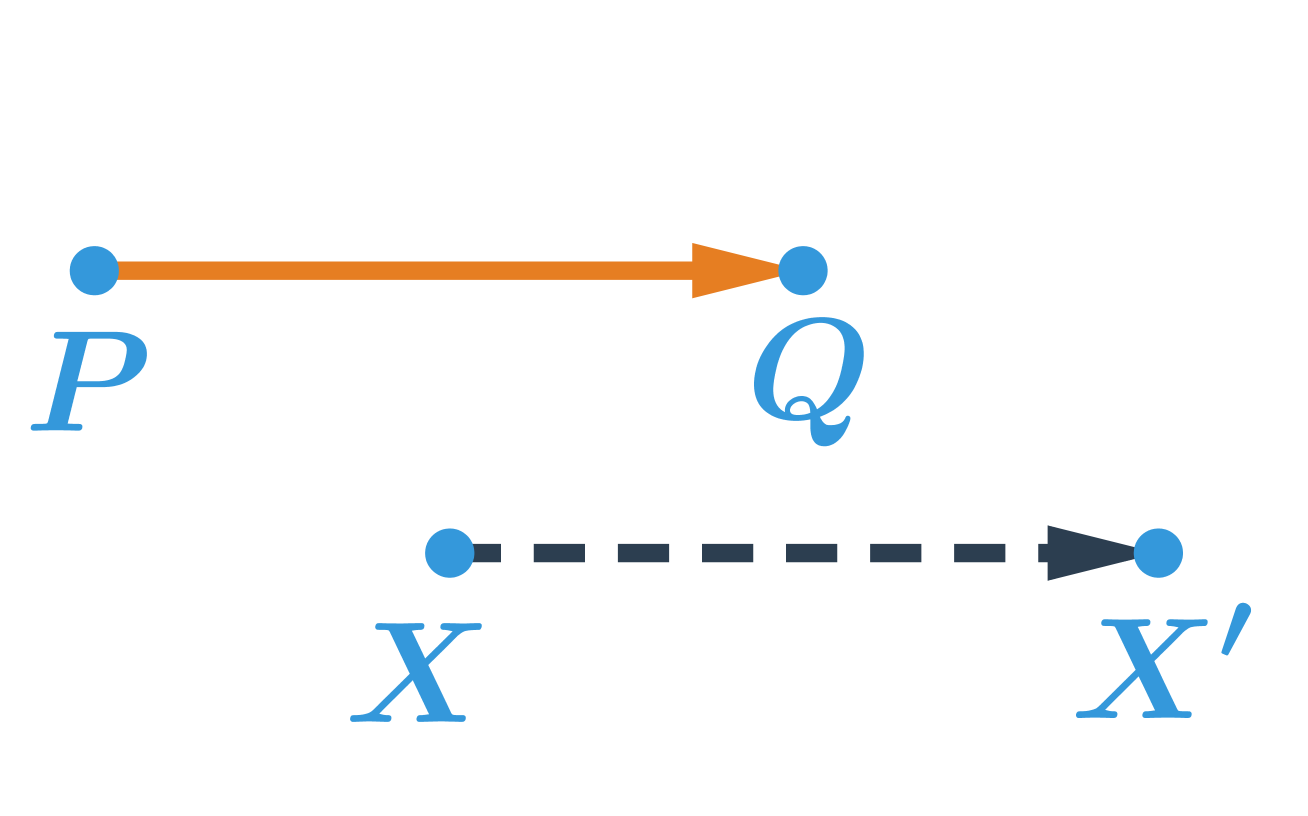
Príklad: posunutie trojuholníka
Obrazom trojuholníka ABC v posunutí, ktoré je určené orientovanou úsečkou \overrightarrow{PQ}, je trojuholník A'B'C': 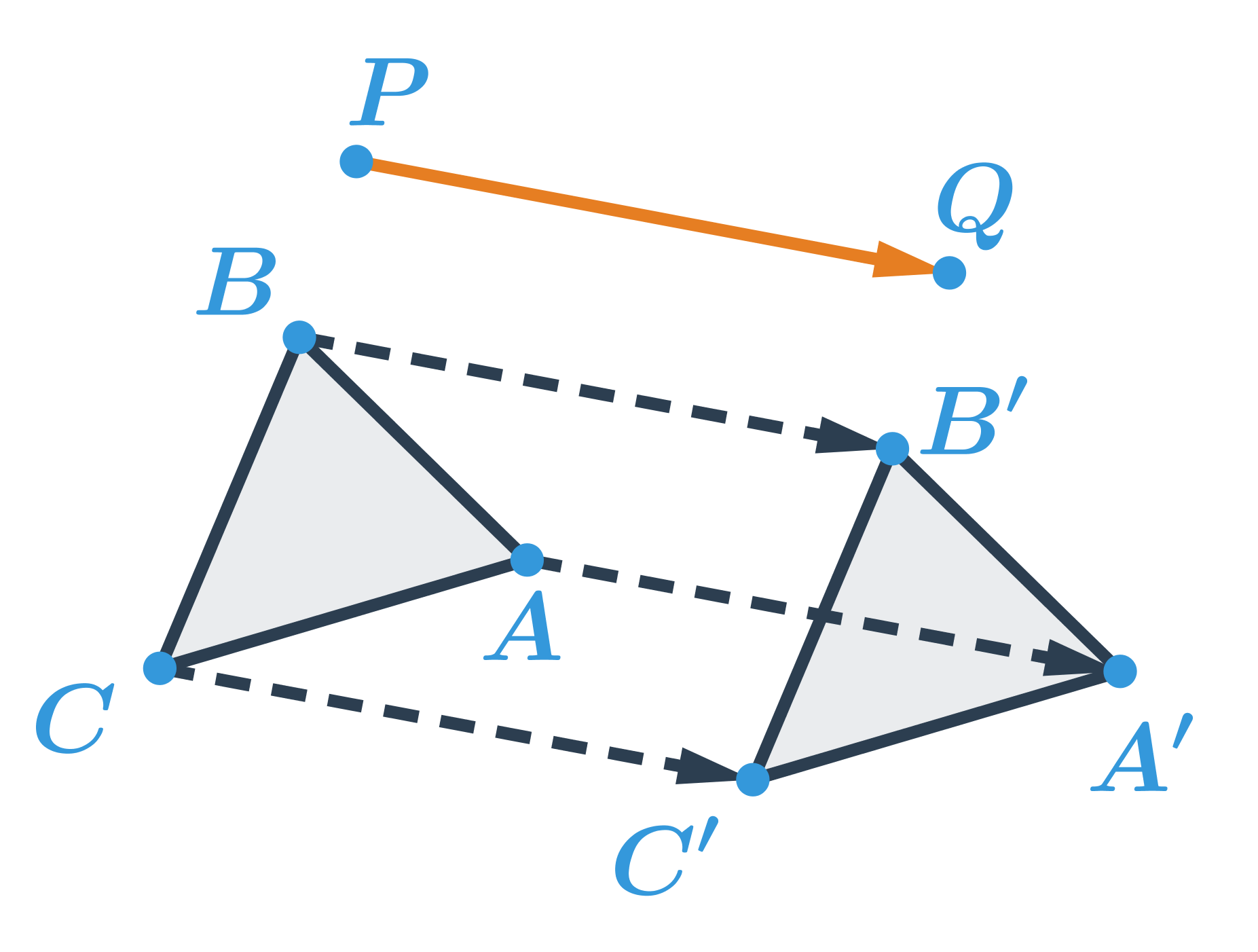
Posunutie zachováva vzdialenosti aj uhly, ide teda o druh zhodnosti.
Posunutie s použitím vektorov
Posunutie môžeme definovať ešte druhým spôsobom, ak poznáme vektory. Posunutie je potom dané vektorom posunutia \vec{u}. Obrazom bodu X je bod X', pre ktorý platí, že vektor \overrightarrow{XX'} má rovnakú veľkosť a rovnaký smer ako vektor \vec{u}.
Príklad: posunutie bodu dané vektorom
Obrazom bodu X v posunutí, ktoré je určené vektorom \vec{u}, je bod X':
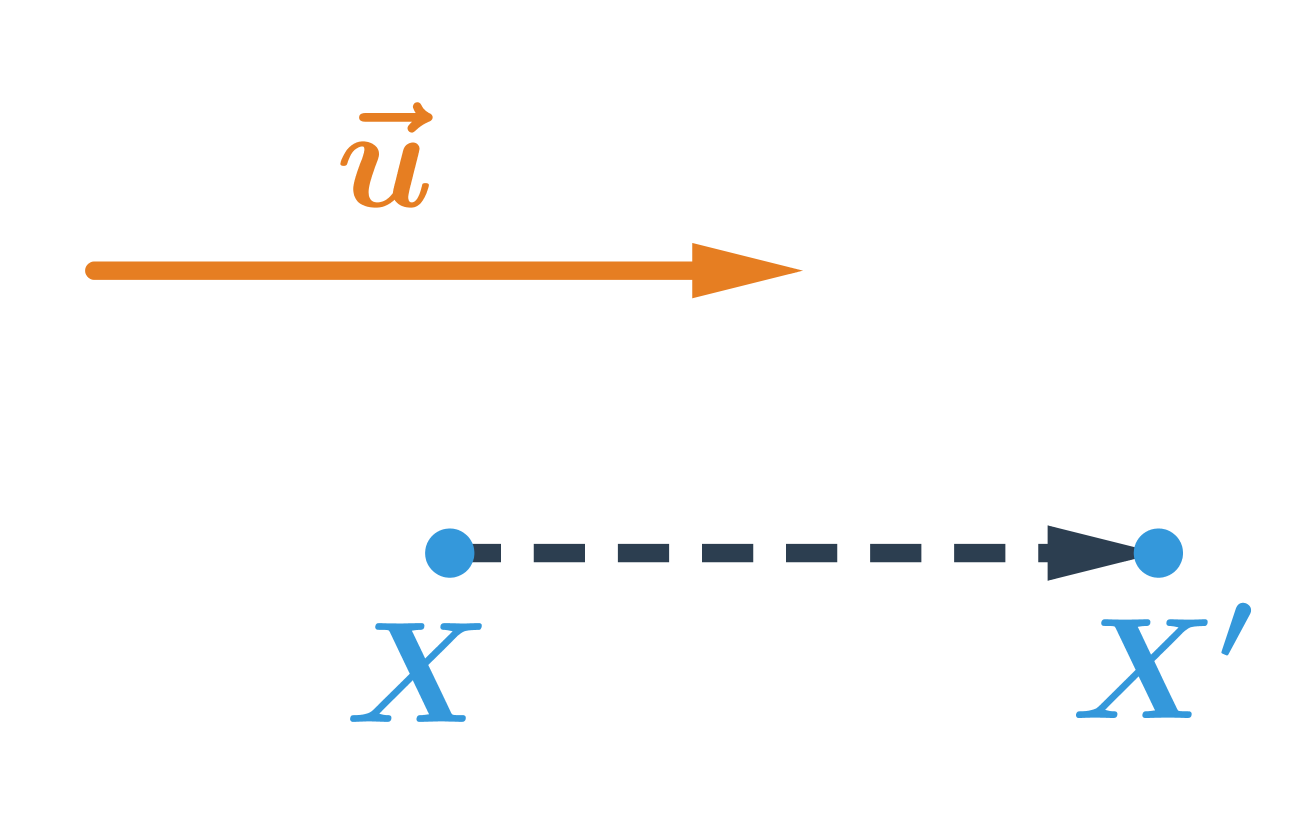
Príklad: posunutie trojuholníka dané vektorom
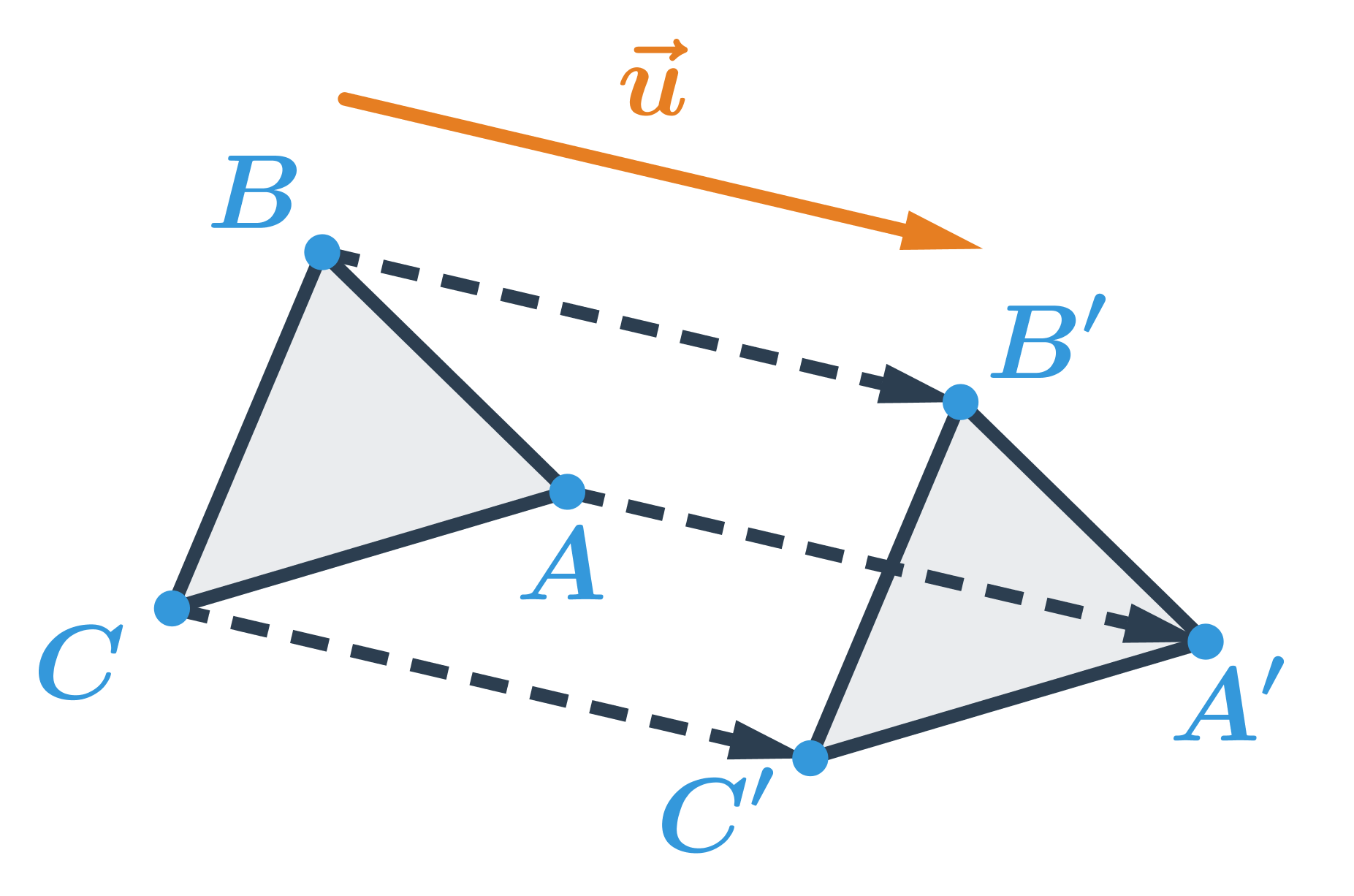
Obrazom trojuholníka ABC v posunutí, ktoré je určené vektorom \vec{u}, je trojuholník A'B'C':
Otočenie (rotácia) je dané bodom S a orientovaným uhlom \alpha. Bod S sa nazýva stred otočenia. Pojem orientovaný uhol znamená, že rozlišujeme, či otáčame proti smeru hodinových ručičiek (kladný smer) alebo po smere hodinových ručičiek (záporný smer). Obrazom bodu X je bod X', ktorý má rovnakú vzdialenosť od stredu S ako bod X a uhol XSX' má veľkosť \alpha.
Príklady
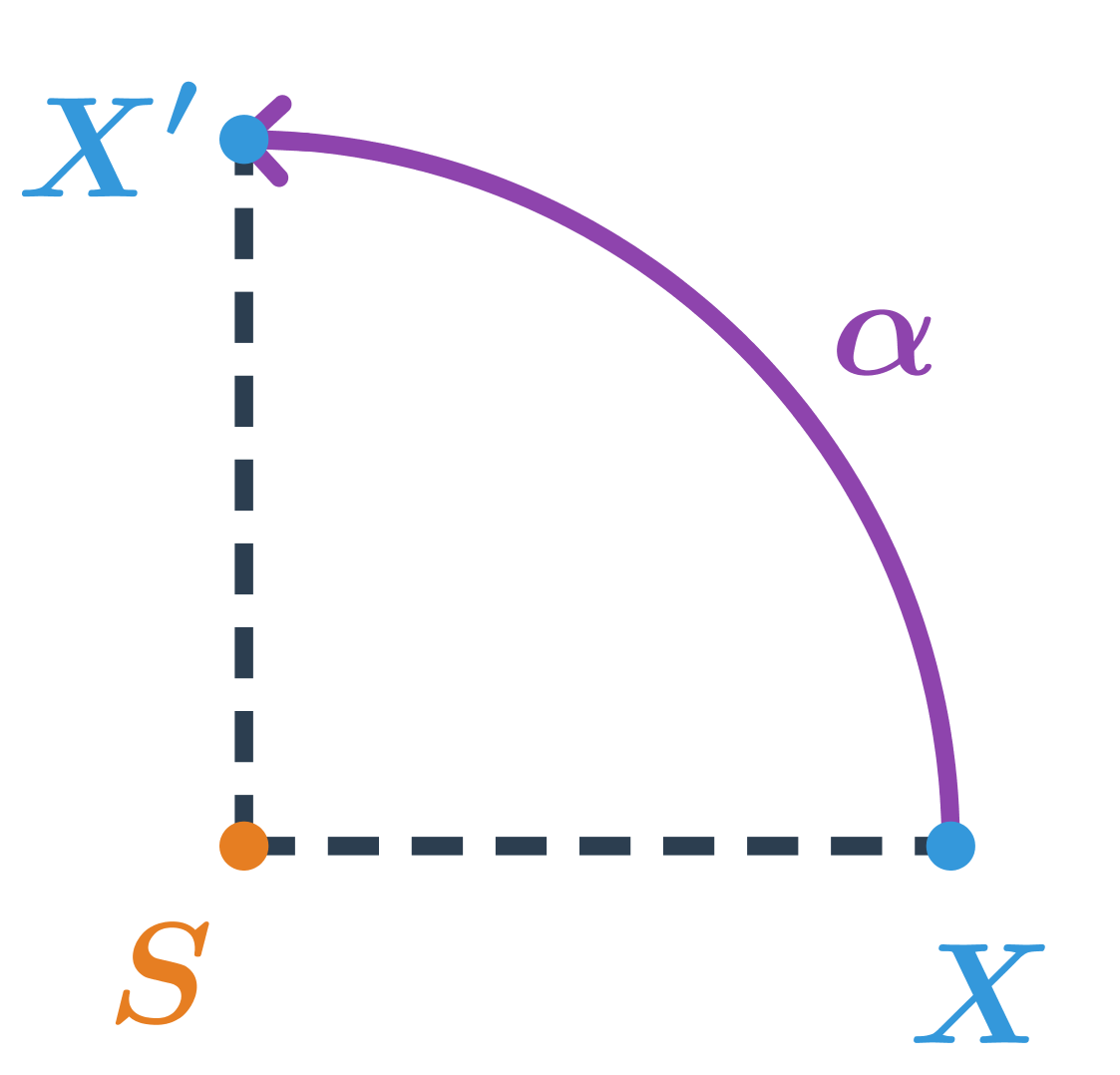
Bod X je otočený okolo stredu S o 90^\circ proti smeru hodinových ručičiek.
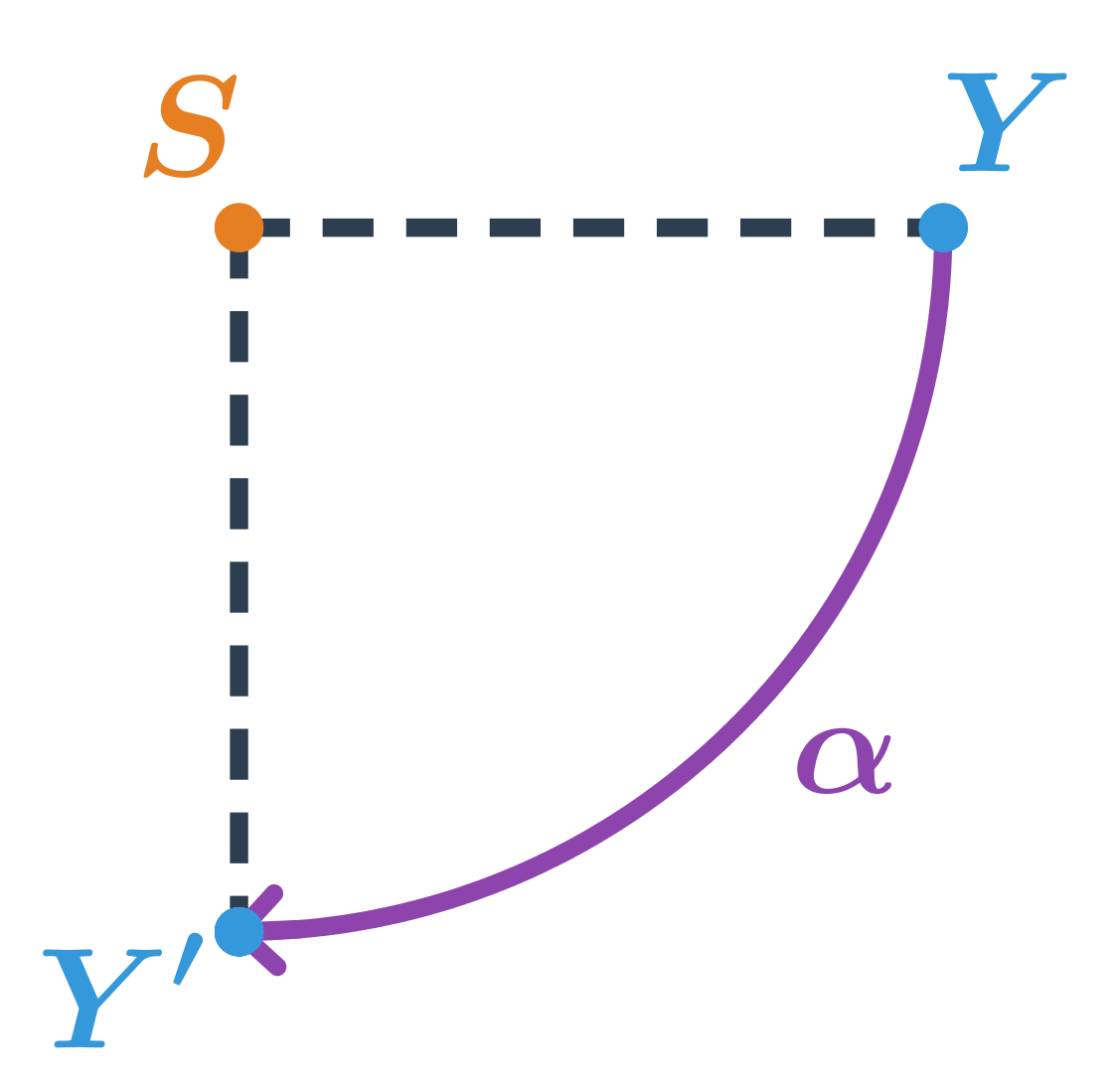
Bod Y je otočený okolo stredu S o 90^\circ v smere hodinových ručičiek, teda o uhol \alpha=-45^\circ
Trojuholník ABC je otočený okolo stredu S o 60^\circ v smere hodinových ručičiek.
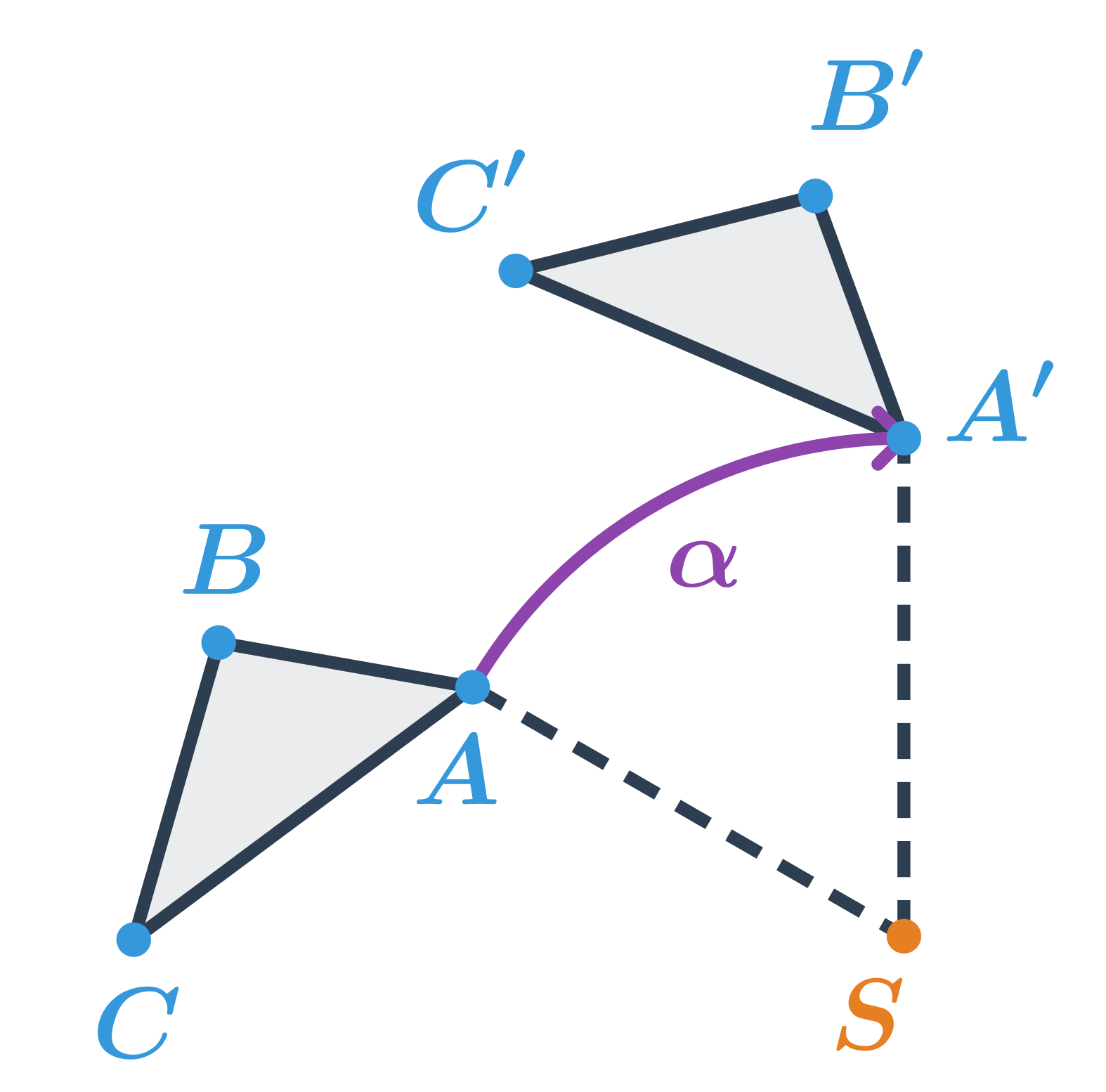
Otočenie zachováva vzdialenosti aj uhly, ide teda o druh zhodnosti.
HoreRovnoľahlosť
Rovnoľahlosť je daná bodom S a nenulovým číslom \lambda. Bod S sa nazýva stred rovnoľahlosti, číslo \lambda je koeficient rovnoľahlosti.
Obrazom bodu X je bod X', pre ktorý platí:
- |SX'|=|\lambda| \cdot |SX|
- pre \lambda \gt 0 leží X, X' na rovnakej polpriamke s počiatkom S
- pre \lambda \gt 0 leží X, X' na opačných polpriamkach s počiatkom S
Na obrázku je vidieť, kde leží obraz X' bodu X v závislosti od hodnoty koeficientu \lambda:
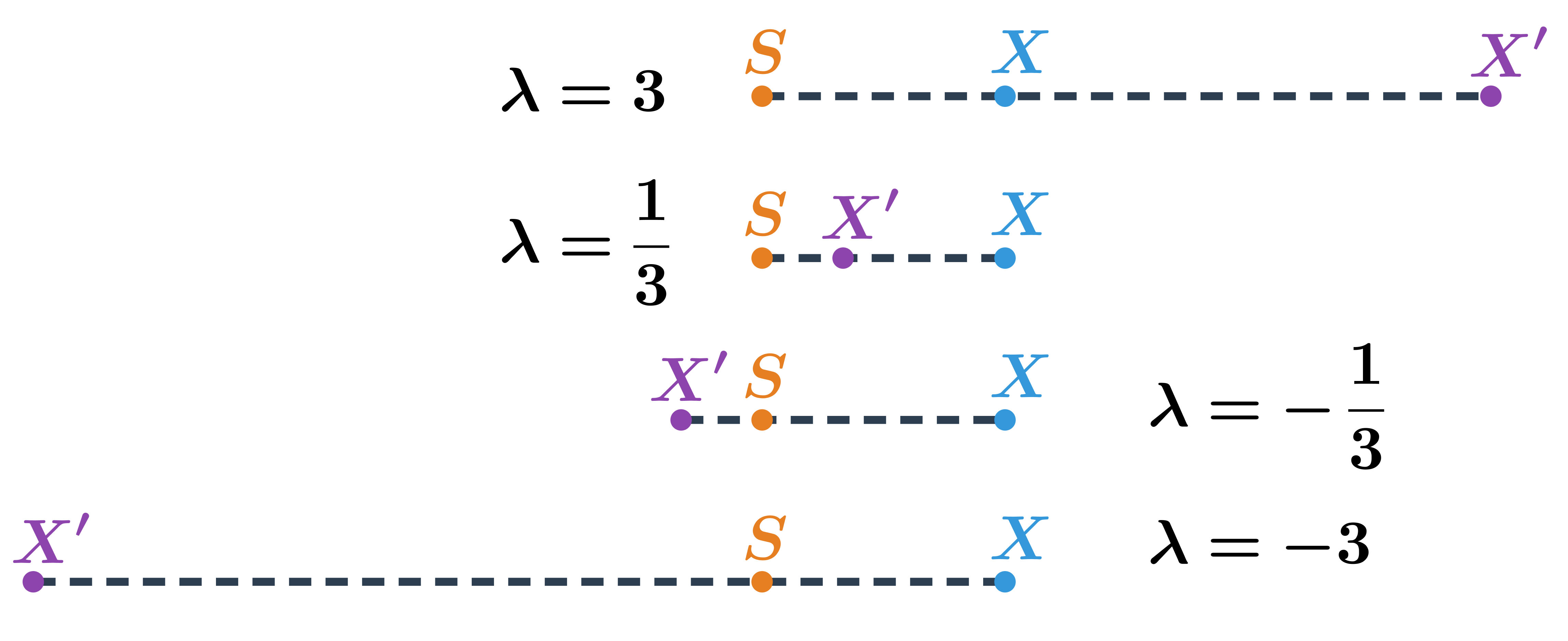
Prehľad vlastností obrazu X' bodu X v rovnoľahlosti so stredom S pre rôzne hodnoty koeficientu \lambda:
| \lambda \gt 0 | bod X' leží na polpriamke SX |
| \lambda \lt 0 | bod X' leží na polpriamke opačnej k SX |
| |\lambda| \gt 1 | bod X' má od stredu S väčšiu vzdialenosť než bod X |
| |\lambda| \lt 1 | bod X' má od stredu S menšiu vzdialenosť než bod X |
Príklad 1: obraz trojuholníka v rovnoľahlosti
Obraz trojuholníka ABC v rovnoľahlosti so stredom S a koeficientom \lambda =\frac{1}{2}
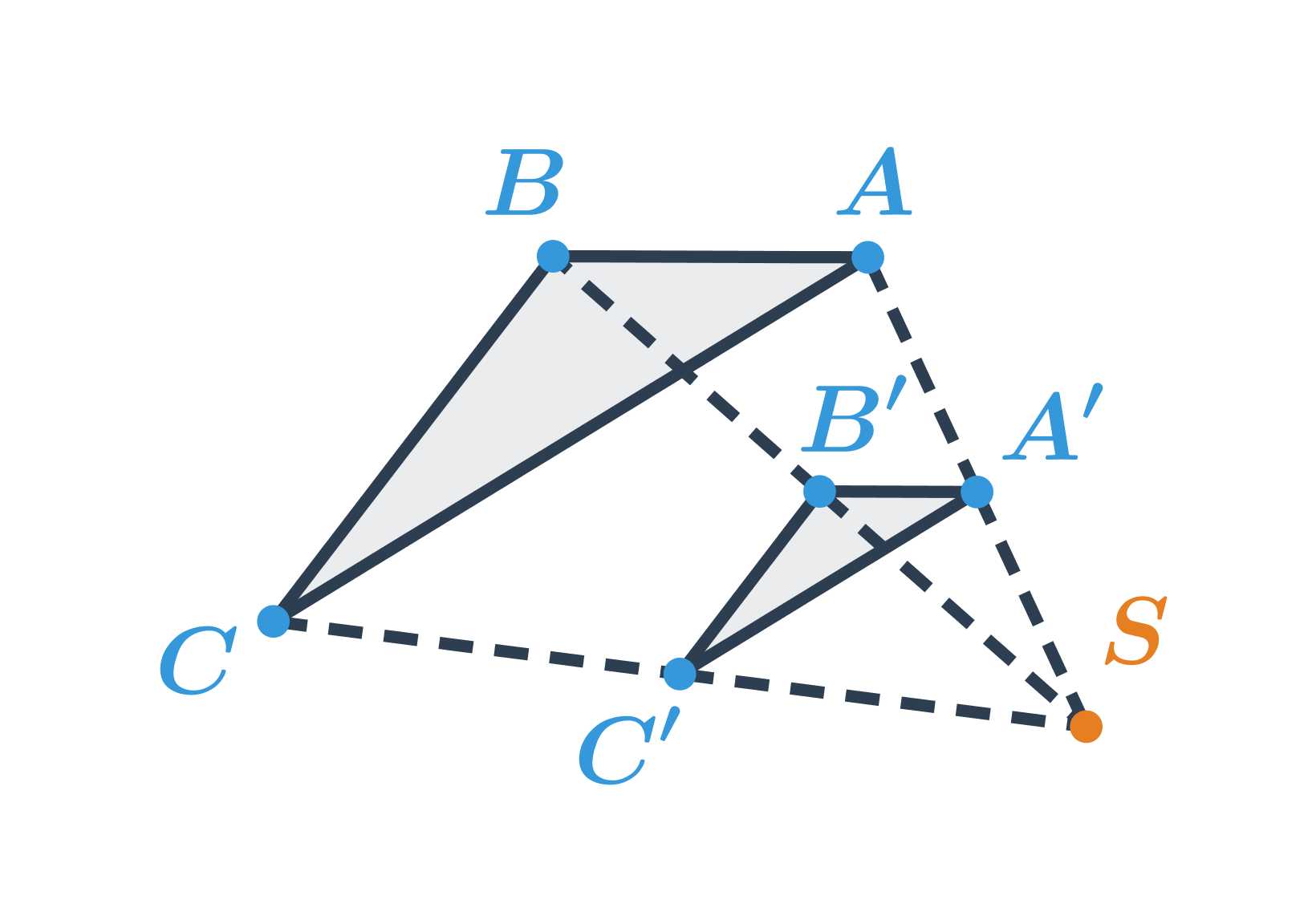
Pre dĺžky zodpovedajúcich si úsečiek platí: \frac{|SA'|} {|SA|}=\frac{|SB'|} {|SB|}=\frac{|SC'|} {|SC|}=\frac{1}{2}
Príklad 2: obraz kružnice v rovnoľahlosti
Obraz kružnice k v rovnoľahlosti so stredom S a koeficientom \lambda =-3.
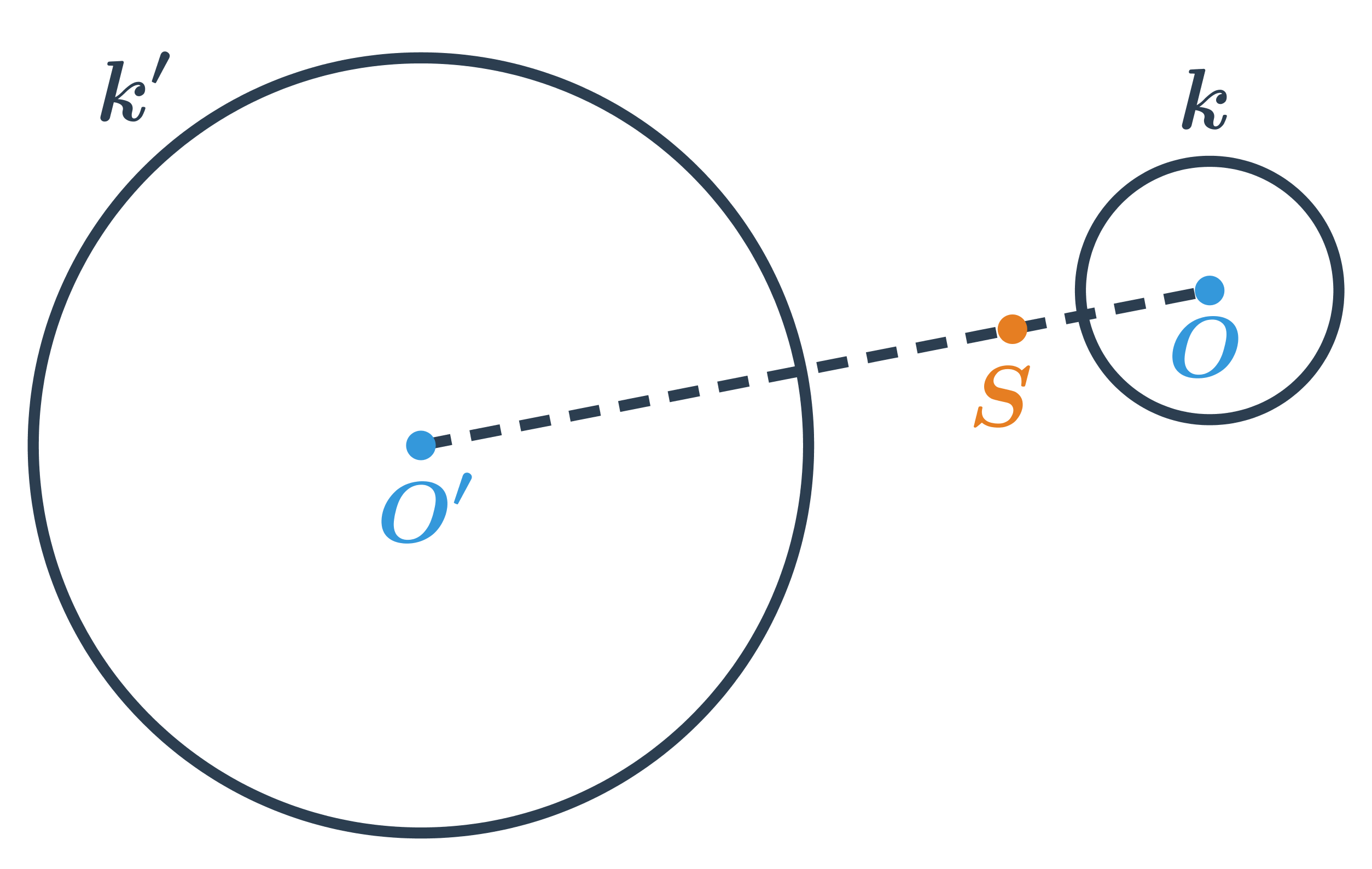
Rovnoľahlosť zachováva uhly a pomer dĺžok, ide teda o druh podobnosti.
Hore
